Evaluation of the applicability of a buoyancy-modified turbulence model for free surface flow analysis based on the VOF method

Du Han Lee

doi:10.3741/JKWRA.2024.57.8.493

Preview

Research Article

Journal of Korea Water Resources Association. 31 August 2024. 493-507
https://doi.org/10.3741/JKWRA.2024.57.8.493

Evaluation of the applicability of a buoyancy-modified turbulence model for free surface flow analysis based on the VOF method

VOF 기반 자유수면 흐름 해석을 위한 부력 수정 난류 모형의 적용성 평가

Du Han Lee^a^*

이 두한^a^*

^aSenior Research Fellow, Department of Hydro Science and Engineering Research, Korea Institute of Civll Engineering and Building Technology, Goyang, Korea

^a한국건설기술연구원 수자원하천연구본부 선임연구위원

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by/4.0):

©It is identical to the Creative Commons Attribution Non-commercial License (https://creativecommons.org/licenses/by/4.0)

ABSTRACT

RANS-based CFD analysis is widely applied in various engineering fields, including practical hydraulic engineering, due to its high computational efficiency. However, problems of non-physical behavior in the analysis of two phase flow, such as free surfaces, have long been raised. The two-equation turbulence models used in general RANS-based analysis were developed for single phase flow and simulate unrealistically high turbulence energy at the interface where there are abrupt changes in fluid density. To solve this issue, one of the methods recently developed is the buoyancy-modified turbulence model, which has been partially validated in coastal engineering, but has not been applied to open channel flows. In this study, the applicability of the buoyancy-modified turbulence model is evaluated using the VOF method in the open-source program OpenFoam. The results of the uniform flow showed that both the buoyancy-modified $k - ϵ$ model and the buoyancy-modified $k - ω$ SST model effectively simulated the reduction of turbulence energy near the free surface. Specifically, the buoyancy-modified $k - ω$ SST model accurately simulated the vertical velocity distribution. Additionally, the model is applied to dam-break flows to examine cases with significant surface variation and cavity formation. The simulation results show that the buoyancy-modified turbulence models produce varying results depending on the VOF method and shows non-physical behavior different from experimental results. While the buoyancy-modified turbulence model is applicable in cases with stable surface shapes, it still has limitations in general application when there are rapid changes in the free surface. It is concluded that appropriate adjustments to the turbulence model are necessary for flows with rapid surface changes or cavity formation.

Keywords

RANS

Buoyancy-modified turbulence model

Turbulent kinetic energy

OpenFoam

Two phase flow

RANS 기반의 CFD 해석은 계산 효율성이 높아 실무 수리해석을 포함한 다양한 공학 분야에서 널리 적용되고 있으나 자유수면과 같이 이상유체흐름 해석에서 비물리적인 거동이 나타나는 문제가 오랫동안 제기되어 왔다. 일반적인 RANS 기반의 해석에서 적용되는 2 방정식 난류 모형은 단상 유체를 대상으로 개발되어 유체 밀도의 급격한 변화가 발생하는 이상유체에서는 경계면에서 실제와 다른 높은 난류 에너지 생성을 모의한다. 최근 이를 해결하기 위해 개발된 방법 중의 하나인 부력 수정 난류 모형은 해안 분야에 적용되어 일부 적합성이 검증되었으나 개수로 흐름에 적용된 사례는 없다. 본 연구에서는 오픈 소스 프로그램인 OpenFoam의 VOF 기법을 기반으로 부력 수정 난류 모형의 적용성을 평가하였다. 등류 흐름 적용 결과에 의하면 부력 수정 $k - ϵ$ 모형과 부력 수정 $k - ω$ SST 모형이 자유수면 부근에서의 난류 에너지 저감 현상을 잘 모의함을 확인하였으며, 특히 부력 수정 $k - ω$ SST 모형은 연직 유속 분포를 잘 모의함을 확인하였다. 또한 댐 붕괴 흐름에 적용하여 수면형의 변동이 크고 공동이 형성되는 경우에 대해 검토하였다. 모의 결과 부력 수정 난류 모형은 VOF 기법에 따라 상이한 결과를 나타내며 실험결과와 다른 비물리적인 거동을 나타내었다. 부력 수정 난류 모형이 수면이 안정적인 형태인 경우에는 적용성이 있으나 자유 수면의 급격한 변화가 발생하는 경우에 범용적으로 적용하기에는 여전히 한계가 있는 것으로 나타났다. 수면형이 급격하게 변화하거나 공동이 형성되는 흐름의 경우에는 난류 모형에 대한 적절한 보정이 필요한 것으로 판단된다.

키워드

RANS

부력 수정 난류 모형

난류 운동 에너지

OpenFoam

이상유체흐름

MAIN

1. 서 론
2. 연구 방법
2.1 지배방정식 및 VOF 기법
2.2 난류 모형
3. 적용 및 결과 분석
3.1 등류 흐름 적용 결과
3.2 댐 붕괴 흐름 적용
4. 요약 및 결론

1. 서 론

CPU와 GPU의 발전으로 수리해석 분야에서 3차원 CFD 모형의 활용은 꾸준이 늘어나고 있다. 실무 수리해석에서 대상 흐름은 대부분 자유수면(free surface)이 있는 개수로 흐름으로 Reynolds averaged Navier-Stokes Equation (RANS) 기반으로 $k - ϵ$ 모형 또는 $k - ω$ SST 모형 등의 난류 모형을 적용하고 자유수면 해석을 위해 Volume of Fluid (VOF) 기법을 적용하고 있다.

RANS 기반의 CFD 해석은 계산 효율성이 높아 실무 수리해석을 포함한 다양한 공학 분야에서 널리 적용되고 있으나 자유수면과 같이 이상유체흐름(two phase flow) 해석에서 비물리적인 거동이 나타나는 문제가 오랫동안 제기되어 왔다. 난류 생성은 유체 내의 변형률에 의해 결정되는데 이상유체의 경계면, 즉, 자유수면에서의 유체 밀도의 급격한 차이는 높은 난류 운동에너지 생성을 유발한다. 실제로 자유수면의 존재는 흐름과 평행하게 난류를 이송하고 자유수면에 연직 방향으로 난류 에너지를 소멸시키지만, 일반적인 RANS 기반의 해석에서는 이를 고려하지 못하고 있다(Kamath et al., 2019).

Bradford (2000)는 $k - ϵ$ 모형을 적용한 쇄파모의에서 쇄파고를 낮게 모의하는 문제를 지적하였으며, Mayer and Madsen (2001)은 $k - ω$ 모형을 적용한 쇄파모의에서 자유수면 부근에서의 과도한 난류 운동에너지 생성을 지적하면서 이를 해결하기 위해 수정 $k - ω$ 모형을 적용하였다. Jacobsen et al. (2014), Fernandez-Mora et al. (2017), Zhou et al. (2017), Christensen (2006), Xie (2013), Brown et al. (2016) 등도 자유수면 경계면에서의 난류 운동에너지의 과대모의를 지적하였다. 이는 기존의 난류모형들이 단상유체흐름(single phase flow)을 대상으로 개발되어 발생한 문제로 인식되고 있다(Devolder et al., 2018). 반면에 VOF를 기반으로 하는 Large Eddy Simulation (LES) 경우에는 유체 경계면에서 난류 운동에너지 과대 산정의 문제는 나타나지 않는다. Xie et al. (2022)에 의하면 VOF 기반의 LES 해석 결과는 개수로 등류 조건에서 실험 결과와 매우 유사한 유속 경사와 난류 운동에너지 경사를 나타낸다. 다만, Mukha et al. (2022)에 의하면 VOF 기반 LES 해석은 과도한 계산시간이 소요되며, 표면 장력과 밀도 경사에 기인하는 수치적 불안정성이 높아 수렴이 쉽지 않은 문제가 있다.

RANS 기반 모의 시에 이상유체의 경계면에서 발생하는 난류 에너지의 비물리적인 모의를 해결하기 위해서 Egorov et al. (2004)는 자유수면 경계면을 고체 경계면과 유사하게 고려하는 난류 감세(turbulence dampinng) 기법을 제안하였으며 Frederix et al. (2018)은 이를 개선하여 일반적인 CFD 코드에 적용할 수 있도록 개선하여 제안하였다. Egorov et al. (2004)의 기법은 ANSYS Fluent (ANSYS Fluent, 2016)에 적용되었으며, Frederix et al. (2018)의 기법은 OpenFoam Foundation 버전(openfoam.org)에 적용되어 있다. Devolder et al. (2018)은 기존 난류모형에 유체간 경계면에서 난류 운동에너지를 감세하는 부력항을 추가하는 부력 수정(buoyancy-modified) $k - ω$ 모형과 부력 수정 $k - ω$ SST 모형을 개발하여 규칙파의 쇄파 모의에 적용하여 제안된 모형의 적용성을 검증하였다. ESI 그룹의 OpenFOAM® 버전(www.openfoam.com)에는 Devolder et al. (2018)의 기법에 따른 부력 수정 $k - ω$ 모형, 부력 수정 $k - ω$ SST 모형, 부력 수정 $k - ϵ$ 모형 등을 제공하고 있다.

이상과 같이 자유수면 흐름에 대한 3차원 CFD 해석에서 발생하는 2 방정식 난류모형의 비물리적인 거동을 보정하기 위한 난류모형이 최근 개발되었으나 수리분야에서 충분한 검증이 이루어지지는 않았다. 본 연구에서는 Devolder et al. (2018)이 개발하여 OpenFOAM®에 구현한 부력 수정 난류 모형을 수리분야에 적용하여 모의 특성을 평가하고자 한다. Frederix et al. (2018)의 기법은 흐름 조건에 따른 경험적인 인자를 적용하여야 하는데, 본 연구 과정에서 이 인자의 설정에 따라 자유수면 경계면에서 물의 유속이 과도하게 산정되는 경향을 확인하여 대상에서 제외하였다.

2. 연구 방법

2.1 지배방정식 및 VOF 기법

본 연구에서는 다양한 분야에 적용되어 신뢰성이 확보된 OpenFOAM 코드의 최신 버전(v2312)을 이용하였다. 이상유체 흐름 해석을 위한 VOF 기법 솔버(solver)는 interFoam과 interIsoFoam을 적용하였다. 난류모형은 개수로 흐름의 적용성을 고려하여 ① $k - ϵ$ 모형, ② $k - ω$ SST 모형, ③ 부력 수정 $k - ϵ$ 모형, ④ 부력 수정 $k - ω$ SST 모형 등을 적용하였다.

interFoam과 interIsoFoam은 이상유체에 대한 비압축성 RANS 방정식이 지배방정식이다. Navier-Stokes 방정식에 레이놀즈 평균화(Reynolds averaging)와 Boussinesq 가정을 적용하면 난류와점성 모형의 적용이 가능한 RANS 방정식으로 표현된다. 여기에 생성항으로 중력가속도와 표면장력을 고려하면 다음과 같이 이상유체에 대한 비압축성 RANS 방정식으로 표현된다.

(1)

\frac{\partial \bar{u_{i}}}{\partial x_{i}} = 0

(2)

\frac{\partial ρ \bar{u_{i}}}{\partial t} + \frac{\partial ρ \bar{u_{i}} \bar{u_{j}}}{\partial x_{j}} = - \frac{1}{ρ} (\frac{\partial \bar{p}}{\partial x_{i}} + \frac{2}{3} ρ \partial k \partial x_{i}) + \frac{\partial}{\partial x_{j}} [\frac{1}{ρ} (μ + μ_{t}) \frac{\partial \bar{u_{i}}}{\partial x_{j}}] + ρ g_{i} + σ κ \frac{\partial α}{\partial x_{i}}

여기서 $t$ 는 시간, $\bar{u_{i}}$ 는 레이놀즈 평균 유속, 𝜌는 유체 밀도, 𝜇는 점성계수, $μ_{t}$ 는 난류와점성계수, $\bar{p}$ 는 레이놀즈 평균 압력, $k$ 는 난류 운동 에너지 등을 나타내며, $g_{i}$ 는 중력가속도 성분, 𝜎는 표면장력 계수, 𝜅는 유체간 경계면의 평균 곡률, 𝛼는 유체 체적분율(volume fraction) 등을 나타낸다.

interFoam과 interIsoFoam는 이상유체(two phase fluid) 솔버로 VOF 기법을 기반으로 한다. VOF 기법은 실무 CFD에서 널리 적용되고 있는 자유수면 추적 기법으로 Hirt and Nichols (1981)가 처음 제안한 이후 다양한 연구자들에 의해 개선이 이루어져 왔다. VOF 기법은 유속장에서 유체의 상태를 나타내는 체적분율 이송방정식을 해석한다.

체적분율는 셀에서 유체의 부피 비율을 나타내며, 0에서 1까지의 값을 가지는 스칼라 변수로 일반적으로 1은 셀이 완전히 물로 채워진 상태이며, 0은 공기로 완전히 채워진 상태를 나타낸다. 𝛼가 0과 1 사이의 값을 가지면 유체의 경계면, 즉 자유수면이 존재함을 나타낸다. VOF 기법은 각 셀에서 체적분율만 제시하므로 셀 내의 유체 경계면의 명시적인 위치가 필요한 경우에는 인근 셀의 체적분율 분포를 이용하여 유체 경계면을 재구성하는 별도의 알고리즘이 필요하다. 또한, VOF 기법에서 체적분율장(volume fration field)는 스칼라 이송 방정식에 따라 전파된다. 체적분율 이송 방정식은 이산화 기법에 따라 경계면의 확산(diffusion), 진동(wrinking), 흐림(smearing) 등의 비물리적인 현상을 유발할 수 있으므로 고정확도의 이산화 기법을 적용하는 것이 중요하다(Weller, 2008).

interFoam 솔버는 경계면에 가상 압축항을 도입하여 다음과 같이 유체의 예리한 경계면을 모의한다(Weller, 2008; Deshpande et al., 2012).

(3)

\frac{\partial α}{\partial t} + \frac{\partial u_{i} α}{\partial x_{i}} + \frac{\partial u_{c, i} α (1 - α)}{\partial x_{i}} = 0

여기서 마지막 항은 가상 압축항을 나타내며 $u_{c, i} = \min [| u_{i} |, \max (| u_{i} |)]$ 이다.

interFoam은 Marschall et al. (2012), Raeini et al. (2012), Hoang et al. (2013) 등의 다양한 적용을 통해 검증되었으나, 경우에 따라 예리한 경계면을 유지하는데 실패하기도 한다. 또한 가상 압축항 자체의 내재된 특성으로 경계면의 부정확한 이동과 비물리적인 경계면 섭동 등이 발생하기도 한다(Roenby et al., 2016; Roenby et al., 2017).

이를 해결하기 위하여 Roenby et al. (2016)은 isoAdvector라는 기하학적 VOF 기법을 제안하였다. isoAdvector 기법은 경계면 재구성 단계와 경계면 이동 단계에서 새로운 기법을 도입한다. 경계면 재구성 단계에서는 셀 내의 유체 분포를 계산하기 위해 isosurface 계산을 수행하며, 경계면 이동 계산에서는 물리적 계산 시간 간격을 소간격으로 분할하고 소간격 사이에는 경계면이 점진적으로 이동한다는 가정하에 체적비 플럭스를 해석적으로 계산하다. 이 기법은 interFoam 솔버처럼 가상 압축항을 도입하지 않고 셀 형상에 대한 가정이 없어 정확도와 적용성 측면에서 우수한 것으로 알려져 있다(Roenby et al., 2017). OpenFoam의 interIsoFoam 솔버는 isoAdvector 기법을 적용하여 유체간 경계면을 계산한다.

2.2 난류 모형

본 연구에서는 ① $k - ϵ$ 모형, ② $k - ω$ SST 모형, ③ 부력 수정 $k - ϵ$ 모형, ④ 부력 수정 $k - ω$ SST 모형 등의 4가지 난류 모형을 검토하였다.

RANS 기반의 와점성 난류 모형 중 대표적인 모형은 $k - ϵ$ 모형, $k - ω$ 모형, $k - ω$ SST 모형 등이 있다. $k - ϵ$ 모형은 높은 레이놀즈 수의 유동 해석에는 적합하나 낮은 레이놀즈 수에 적용할 수 없는 한계가 있다. $k - ω$ 모형은 점성 하부층을 정확하게 모의하여 레이놀즈 수에 상관없이 적용이 가능하나 자유 흐름의 난류 특성에 민감하게 반응하는 단점을 가진다.

$k - ω$ SST 모형은 $k - ϵ$ 모형과 $k - ω$ 모형의 장점을 결합한 복합 모형으로 벽 경계면에서는 $k - ω$ 모형이 적용되며 자유 흐름 영역에서는 $k - ϵ$ 모형이 적용된다. 와점성계수 $ν_{T}$ , 난류 운동에너지 $k$ , 특정소실율 $ω$ 등에 대한 지배방정식은 다음과 같다(Menter, 1994).

(4)

\frac{\partial k}{\partial t} + \frac{\partial u_{j} k}{\partial x_{j}} - \frac{\partial}{\partial x_{j}} [(ν + σ_{k} ν_{t}) \frac{\partial k}{\partial x_{j}}] = P_{k} - β^{*} ω k

(5)

\frac{\partial ω}{\partial t} + \frac{\partial u_{j} ω}{\partial x_{j}} - \frac{\partial}{\partial x_{j}} [(ν + σ_{w} ν_{t}) \frac{\partial ω}{\partial x_{j}}] = \frac{γ}{ν_{t}} G - β ω^{2} + 2 (1 - F_{1}) \frac{σ_{ω 2}}{ω} \frac{\partial k}{\partial x_{j}} \frac{\partial ω}{\partial x_{j}}

(6)

P_{k} = \min (G, 10 β^{*} k ω), G = ν_{t} \frac{\partial u_{i}}{\partial x_{j}} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}), ν_{t =} \frac{a_{1} k}{\max (a_{1} ω, S F_{2})}

여기서 $k$ 는 난류 운동에너지, $P_{k}$ 는 $k$ 의 생성항, 𝜈는 동점성계수, $ν_{t}$ 는 난류 동점성계수, $ω$ 는 특성 감세율, $S$ 는 흐름의 평균 변형율 등이다. $F_{1}$ 과 $F_{2}$ 는 혼합함수인데, $F_{1}$ 은 벽 경계에서 1이며 벽에서 멀어지면 0이 된다. $σ_{k}$ , $σ_{ω}$ , 𝛾 등은 다음 식에 의해 혼합된다.

(7)

ϕ = ϕ_{1} F_{1} + ϕ_{2} (1 - F_{1})

여기서 각 계수는 다음과 같다.

(8)

F_{1} = \tanh \{{\{\min [\max (\frac{\sqrt{k}}{β^{*} ω y}, \frac{500 ν}{y^{2} ω}), \frac{4 σ_{ω 2} k}{C D_{k ω} y^{2}}]\}}^{4}\}

(9)

F_{2} = \tanh [{[\max (\frac{2 \sqrt{k}}{β^{*} ω y}, \frac{500 ν}{y^{2} ω})]}^{2}]

(10)

C D_{k w} = \max (2 ρ σ_{ω 2} \frac{1}{ω} \frac{\partial k}{\partial x_{i}} \frac{\partial ω}{\partial x_{i}}, 10^{- 10})

(11)

α_{1} = \frac{5}{9}, α_{2} = 0.44

(12)

β_{1} = \frac{3}{40}, β_{2} = 0.0828

(13)

β^{*} = \frac{9}{100}

(14)

σ_{k 1} = 0.85, σ_{k 2} = 1

(15)

σ_{ω 1} = 0.5, σ_{ω 2} = 0.856

VOF 기법에 2 방정식 난류모형을 적용하면 유체간 경계면에서 비정상적인 난류 운동에너지 증가가 발생한다. 이는 밀도차가 큰 유체간 경계면에서 발생하는 매우 큰 속도 경사로 인해 발생하며 이로 인해 공기층에서 비정상적인 속도가 계산되는 것이 원인이다. 또한 이와 같은 비정상적인 공기층 속도는 압력과 밀도가 연계된 지배 방정식을 변수를 분리하여 순차적으로 계산하는 수치계산 알고리즘에서도 기인한다. 즉, 물과 공기층 사이에는 매우 큰 밀도차로 인해 압력 경사와 밀도 경사 사이에 기본적인 불균형이 존재한다. 이를 해결하기 위해 Devolder et al. (2018)은 기존 2 방정식 난류모형에 유체간 경계면에서 난류 운동에너지를 감세하는 부력항을 추가하는 부력 수정 $k - ω$ 모형과 부력 수정 $k - ω$ SST 모형을 개발하여 규칙파의 파쇄 모의에 적용하여 제안된 모형의 적용성을 검증하였다. Devolder et al. (2018)가 제시한 부력 수정 $k - ω$ SST 모형은 다음과 같다.

(16)

\begin{aligned} \frac{\partial ρ k}{\partial t} + \frac{\partial ρ u_{j} k}{\partial x_{j}} - \frac{\partial}{\partial x_{j}} [ρ (ν + σ_{k} ν_{t}) \frac{\partial k}{\partial x_{j}}] = ρ P_{k} + G_{b} - ρ β^{*} ω k \\ \frac{\partial ρ ω}{\partial t} + \frac{\partial ρ u_{j} ω}{\partial x_{j}} - \frac{\partial}{\partial x_{j}} [ρ (ν + σ_{w} ν_{t}) \frac{\partial ω}{\partial x_{j}}] = \frac{γ}{ν_{t}} ρ G - ρ β ω^{2} + 2 (1 - F_{1}) ρ \frac{σ_{w 2}}{ω} \frac{\partial k}{\partial x_{j}} \frac{\partial ω}{\partial x_{j}} \end{aligned}

(17)

\begin{aligned} \frac{\partial ρ ω}{\partial t} + \frac{\partial ρ u_{j} ω}{\partial x_{j}} - \frac{\partial}{\partial x_{j}} [ρ (ν + σ_{w} ν_{t}) \frac{\partial ω}{\partial x_{j}}] = \frac{γ}{ν_{t}} ρ G - ρ β ω^{2} + 2 (1 - F_{1}) ρ \frac{σ_{w 2}}{ω} \frac{\partial k}{\partial x_{j}} \frac{\partial ω}{\partial x_{j}} \end{aligned}

여기서 부력항 $G_{b}$ 는 다음과 같으며, $σ_{t}$ = 0.85이다.

(18)

G_{b} = - \frac{ν_{t}}{σ_{t}} \frac{\partial ρ}{\partial x_{j}} g_{j}

부력 수정 $k - ω$ SST 모형에서 추가된 부력항 $G_{b}$ 는 난류 동점성계수 $ν_{t}$ , 중력 방향의 밀도 경사, 중력, 일종의 보정계수인 $σ_{t}$ 등의 곱으로 표현되는데 여기서 $ν_{t}$ 는 Eq. 16과 Eq. 17로부터 음해법으로 계산된다. 부력항 $G_{b}$ 의 추가로 중력 방향으로 밀도 경사가 큰 경우 $k$ 이송방정식의 생성항이 증가하므로 결과적으로 수평방향의 자유수면에서 난류 에너지를 감세하는 효과를 나타낸다.

3. 적용 및 결과 분석

3.1 등류 흐름 적용 결과

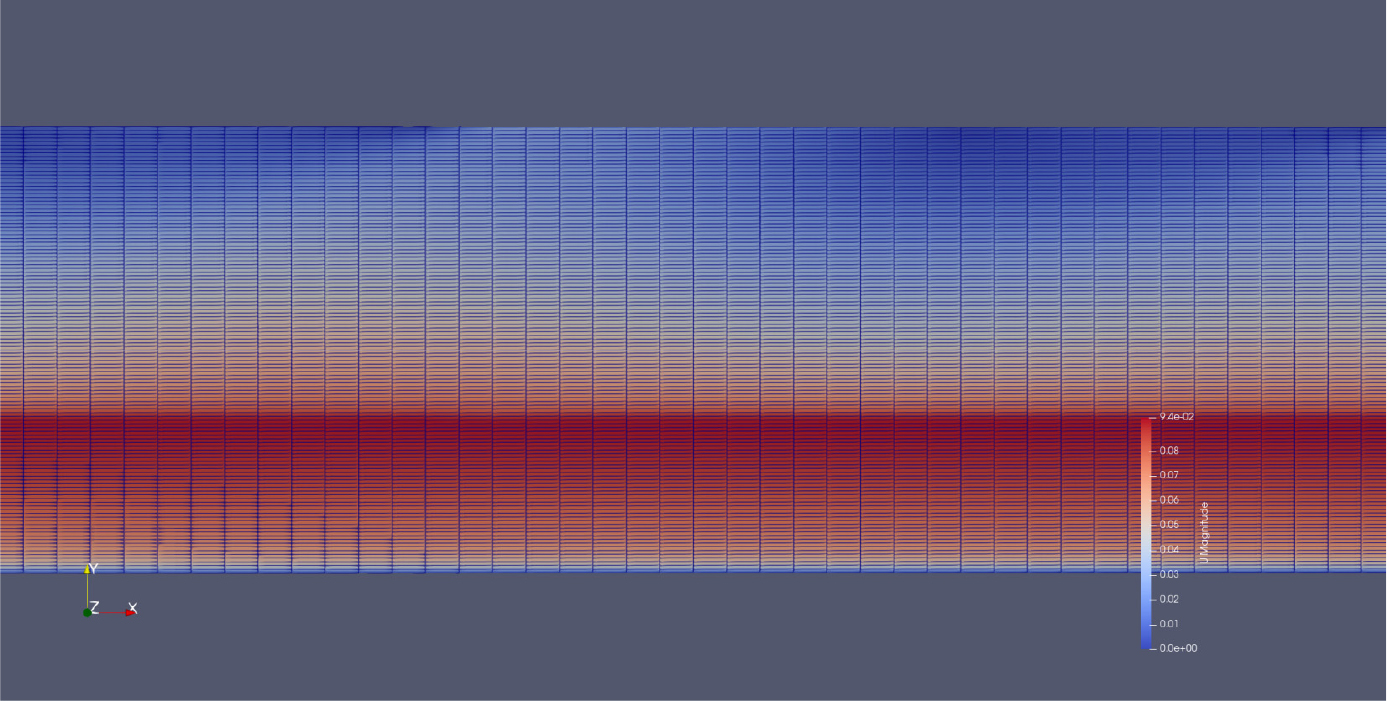
VOF 기법에 적용된 난류모형의 특성을 비교하기 위하여 Nezu and Rodi (1986)의 등류 실험 중 P1 케이스에 적용하여 비교하였다. Nezu and Rodi (1986)는 LDA 측정을 통해 등류 흐름에 대한 유속 분포과 난류강도에 대해 상세한 측정 결과를 제시하였다. 본 연구에서는 길이 18 m, 높이 0.3 m 수로를 연직 2차원으로 구성하였으며, 길이 방향 셀 400개, 높이 방향 셀 240개로 총 96,000개의 셀을 구성하였다. 모의 시간은 3,000 초로 하여 흐름의 시간적 변화가 없을 때까지 모의하였으며, Courant number는 0.5 이하로 유지하면서 모의를 수행하였다. 수로 길이에 따른 수심 변화를 통해 등류 조건이 형성됨을 확인하였다. 이 때 수심 $h$ = 0.101 m이며, 평균 유속 $U_{m}$ = 0.0757 m/s이다. 등류 흐름의 격자 구성은 Fig. 1과 같다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F1.jpg

Fig. 1.

The grid composition for unifrom flow

3차원 모형을 이용한 이상유체흐름에서 개수로의 등류 조건을 조성하기 위해서는 경계조건 설정이 중요하다. 자유수면을 ligid lid 조건으로 설정하는 경우에는 전 구간에서 동일한 수위가 형성되나, 중력이 작용하는 이상유체흐름 모의에서는 상하류 수위가 일정하게 유지되면서 하류경계에서는 연직 유속 분포가 그대로 유지되어야 하므로 이를 만족하는 경계조건의 설정이 필요하다. 본 연구에서 다양한 경계조건을 시험하여 하류부에서 등류에 가까운 수위와 유속분포가 유지되는 조건을 검토하였다. 유입부 경계조건은 유량과 평균 유속에 의해 수심이 자동 계산되는 OpenFoam의 ‘variableHeightFlowRateInletVelocity’ 조건으로 설정하고, 하류 경계조건은 평균 유속에 따라 수심이 자동 설정되는 ‘outletPhaseMeanVelocity’ 조건으로 설정할 경우 등류 조건이 유지되어 이를 적용하였다.

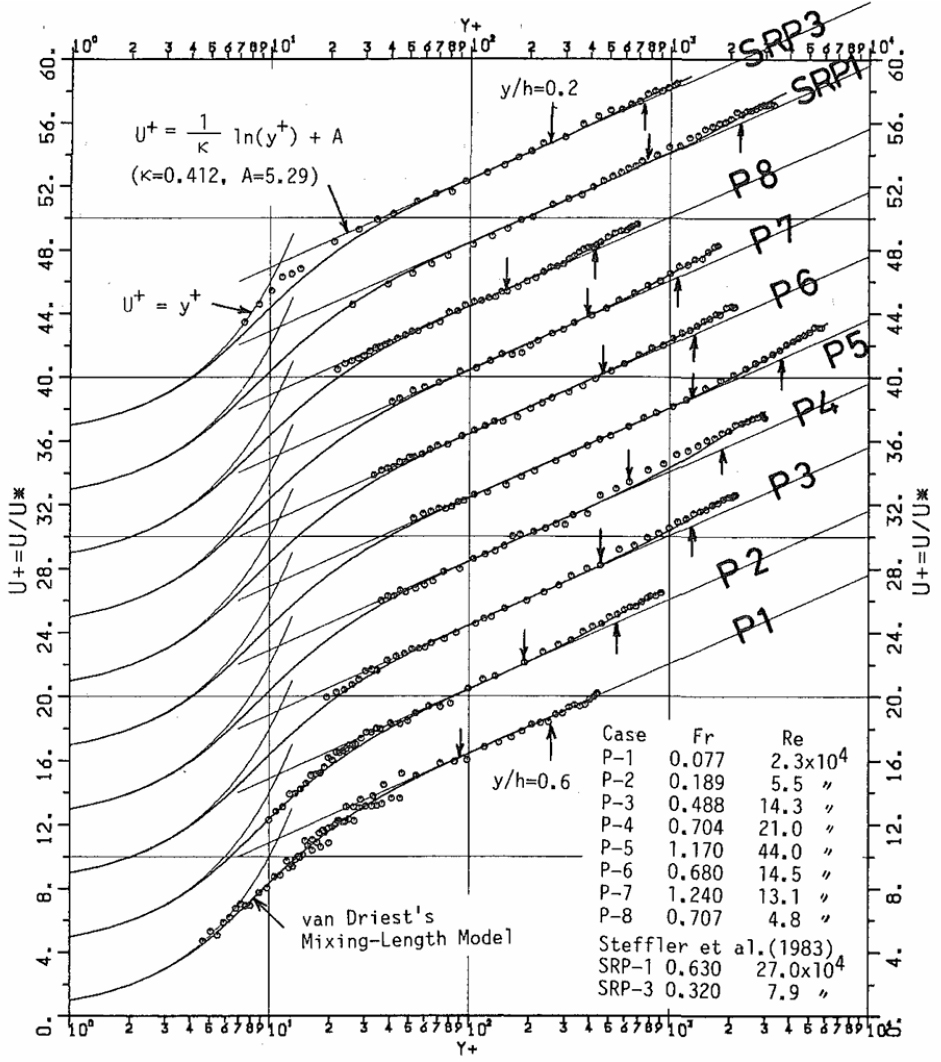
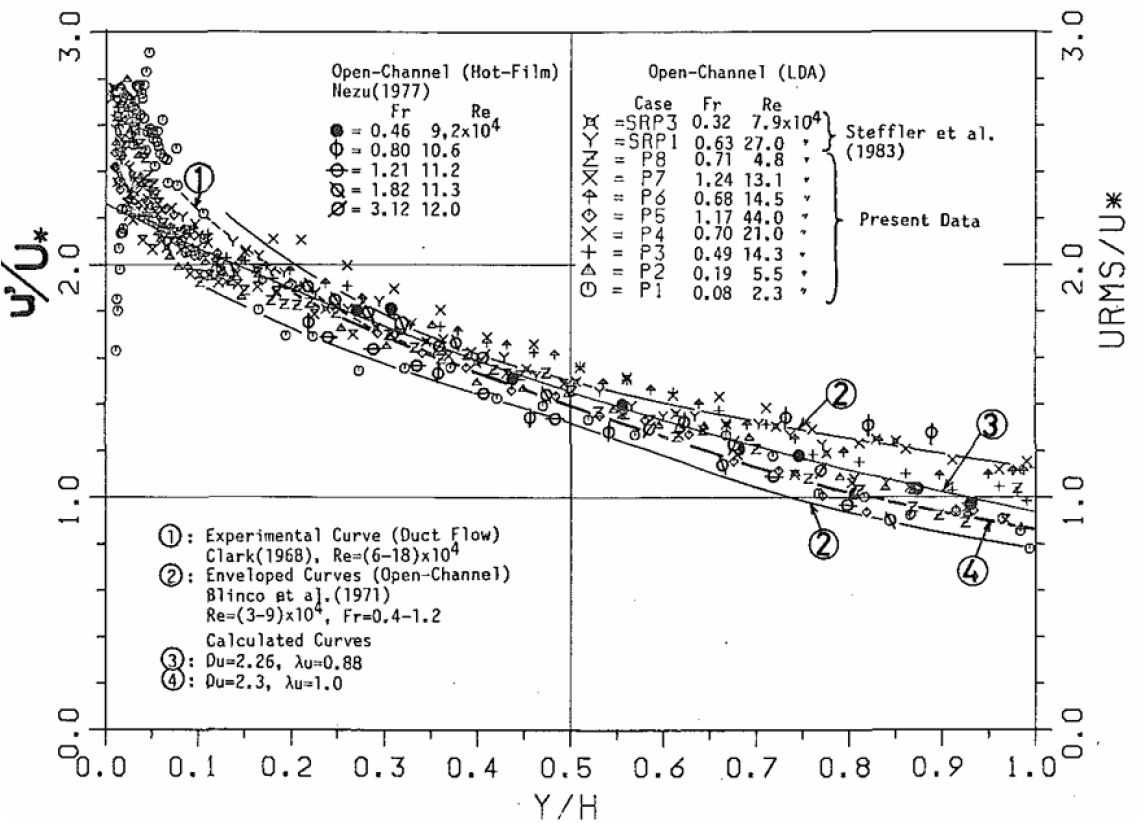
Nezu and Rodi (1986)의 측정 결과 중 로그 스케일에 도시된 무차원 벽 거리 $y^{+}$ 와 무차원 유속 $u^{+}$ 의 관계는 Fig. 2와 같으며, 상대수심(y/H)에 따른 난류강도는 Fig. 3과 같다. 실험에 의한 난류강도는 벽 부근에서는 급격하게 증가하여 최대 3.0 정도의 값을 보이며 수심 증가에 따라 완만하게 감소하여 수면 부근에서는 약 0.8 정도의 값을 보이고 있다. 본 연구에서는 $y^{+}$ 는 5 - 500 사이에 있어, 점성저층, 완충층, 로그 법칙 층 등의 3개 영역에서 유속분포가 이론적인 분포와 잘 일치하는 P1 케이스를 선정하여 비교하였다. P2 케이스는 점성저층에 대한 유속분포가 없으며 그 외의 케이스는 푸르드 수가 증가함에 따라 로그 법칙 층에 대한 유속분포만 있고, 수면 부근에서 유속 감세 현상(wake)이 뚜렷하게 발달하므로 제외하였다. 수면 부근의 유속 감세 현상은 측벽의 영향 또는 바람의 영향으로 발생하는데 본 수치모의에서는 재현이 어려울 것으로 판단하였다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F2.jpg

Fig. 2.

Velocity profiles of Nezu and Rodi expriments (Nezu and Rodi, 1986)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F3.jpg

Fig. 3.

Turbulence intensity of Nezu and Rodi expriments (Nezu and Rodi, 1986)

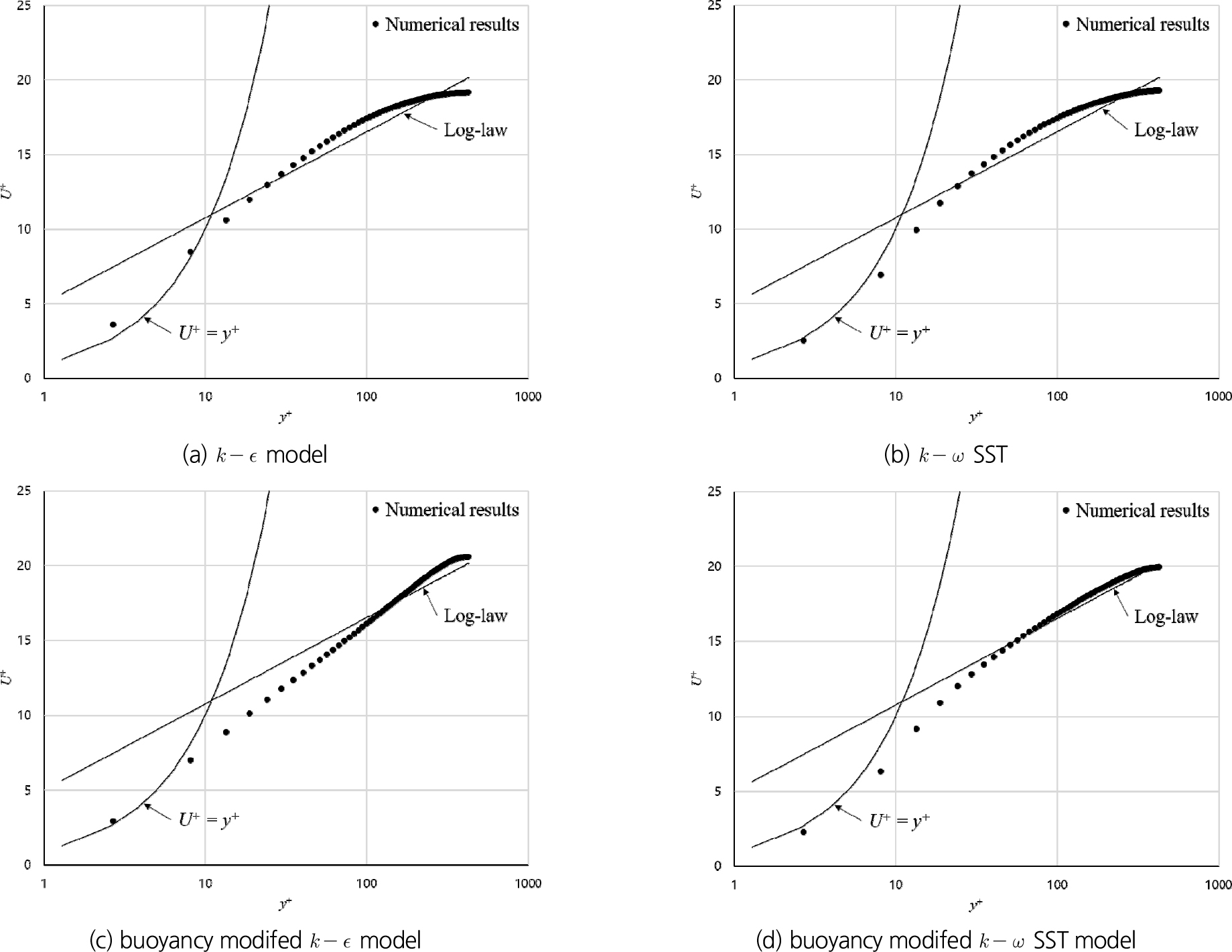
같은 흐름 조건에서 난류 모형은 $k - ϵ$ 모형, $k - ω$ SST 모형, 부력 수정 $k - ϵ$ 모형, 부력 수정 $k - ω$ SST 모형 등의 4개 모형을 적용하여 등류 상태에서의 연직 유속 분포와 연직 난류강도 분포를 비교하였다. 첫 번째 격자의 중심부 위치가 $y^{+}$ = 2.69로 계산되어 격자 구성이 적합함을 확인하였다. 유속 및 난류 분포는 등류가 안정적으로 발달된 상류 유입부에서 17.0 m에 위치한 지점의 값을 선정하였다. 바닥면 부근의 유속 분포 비교를 위해 적용된 난류 모형별 유속 분포 결과를 $y^{+}$ 와 $u^{+}$ 의 관계로 도시하면 Fig. 4와 같다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F4.jpg

Fig. 4.

Velocity profiles of uniform flow condition in $y^{+}$ and $u^{+}$

Fig. 4에 의하면 난류모형에 따라 연직 유속 분포가 다르게 모의됨을 확인할 수 있다. $k - ϵ$ 모형은 점성 저층에서 점성 저층 법칙( $u^{+} = y^{+}$ )과 다소 차이를 보이며 완충층과 로그 법칙 층에서도 이론 분포와 큰 차이를 보이고 있다. $k - ω$ SST 모형은 점성 저층에서는 이론식과 유사한 경향을 보이나 로그 법칙 층에서는 $k - ϵ$ 모형과 유사한 형태로 이론식과 차이를 나타낸다. 부력 수정 $k - ϵ$ 모형은 점성 저층에서는 이론식과 유사한 경향을 보이나 완층층과 로그 법칙 층에서 이론 분포와는 큰 차이를 나타내고 있다. 부력 수정 $k - ω$ SST 모형은 점성 저층과 완충층에서 이론분포와 유사한 경향을 보이며, 로그 법칙 층에서는 로그 법칙과는 다소 차이를 나타내나, 타 난류모형에 비해 비교적 이론식에 가까운 유속 분포를 나타내고 있다.

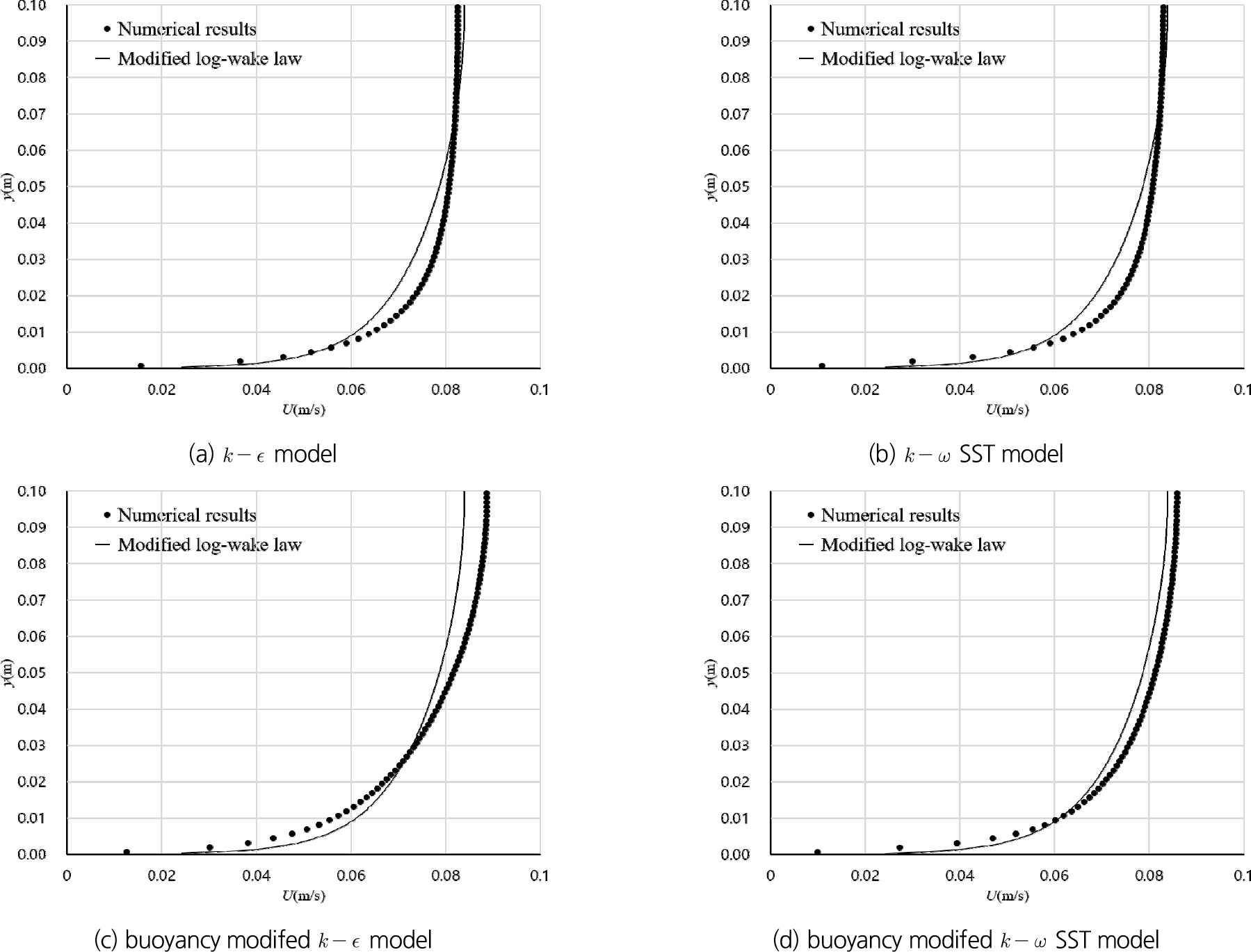
외부 영역과 자유수면 부근의 유속 분포를 비교하기 위하여 Guo et al. (2005)이 제안한 수정 log-wake 법칙을 적용하여 난류모형 별로 비교하면 Fig. 5와 같다. $k - ϵ$ 모형과 $k - ω$ SST 모형은 유사한 경향을 보이는데, 수정 log-wake 법칙에 비해 수심에 따른 속도 경사가 급하게 나타난다. 반면에 부력 수정 $k - ϵ$ 모형과 부력 수정 $k - ω$ SST 모형은 속도 경사가 비교적 완만하게 나타나고 있다. 그러나 부력 수정 $k - ϵ$ 모형은 수정 log-wake 법칙에 비해 지나치게 완만한 속도 경사를 보인다. 부력 수정 $k - ω$ SST 모형은 전체적으로 수정 log-wake 법칙과 유사한 수심별 유속 분포를 나타내고 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F5.jpg

Fig. 5.

Velocity profile comparisons with modified log-wake law

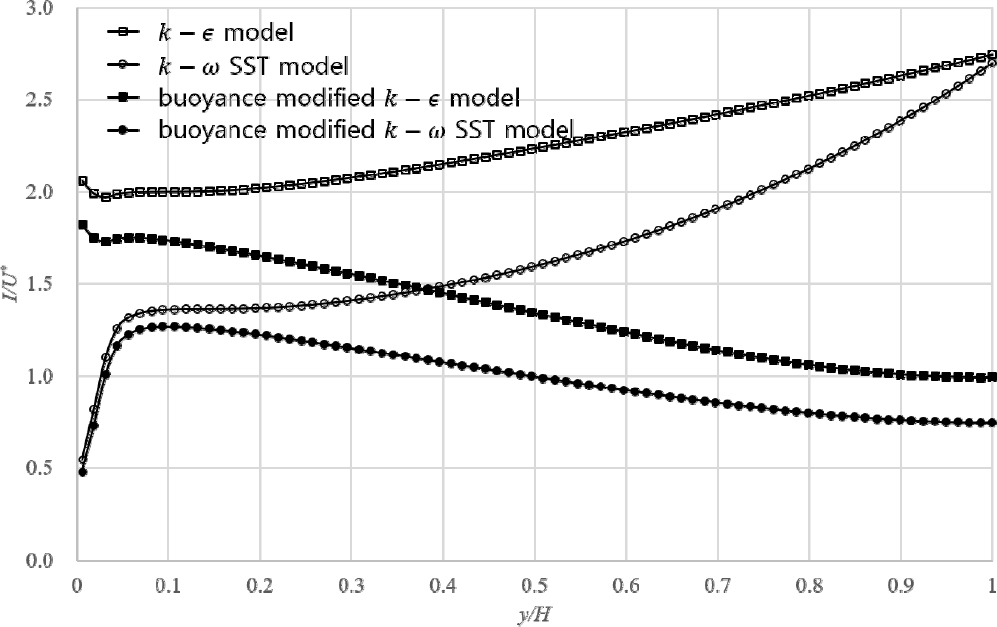
수치모의에서 계산된 난류 운동에너지를 난류강도로 변환하여 수심별 난류강도를 도시하면 Fig. 6과 같다. 수심별 난류강도는 난류모형별로 큰 차이를 나타내는데, 부력 수정이 고려되지 않은 $k - ϵ$ 모형과 $k - ω$ SST 모형은 수심 증가에 따라 난류강도가 증가하는 경향을 보이며 부력 수정 $k - ϵ$ 모형과 부력 수정 $k - ω$ SST 모형은 수심 증가에 따라 난류강도가 감소하는 경향을 나타내고 있다. 벽면 부근에서 난류강도가 증가하는 현상을 $k - ω$ SST 모형과 부력 수정 $k - ω$ SST 모형은 모의하고 있으나, $k - ϵ$ 모형과 부력 수정 $k - ϵ$ 모형은 이 현상을 재현하지 못하고 있다. 전체적인 경향은 부력 수정 $k - ω$ SST 모형이 Nezu and Rodi (1986)의 실험과 부합하는 경향을 보이나, 여전히 바닥면 부근에 발생하는 높은 난류강도를 재현하는데는 한계를 보이고 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F6.jpg

Fig. 6.

Turbulence intensity of selected turbulence models

이상의 결과를 종합하면 VOF 기법에 일반적인 $k - ϵ$ 모형과 $k - ω$ SST 모형을 적용하여 개수로 등류 흐름을 모의하면 수심에 따라 난류강도가 증가하는 비물리적인 거동이 모의되며, 이로 인해 수심별 속도 경사가 실제에 비해 급하게 형성됨을 확인할 수 있다. 이를 개선하기 위한 부력 수정 난류 모형을 적용하면 수심에 따라 난류강도 감소하는 실험 결과의 경향성을 모의하고 있음을 알 수 있다. 그러나 부력 수정 $k - ϵ$ 모형은 유속 경사를 지나치게 완만하게 모의하는 문제가 있으며, 부력 수정 $k - ω$ SST 모형은 실제와 유사한 수심별 유속 경사를 나타내고 있다. 다만, 부력 수정 $k - ω$ SST 모형도 벽 부근의 높은 난류강도를 재현하지는 못한다.

3.2 댐 붕괴 흐름 적용

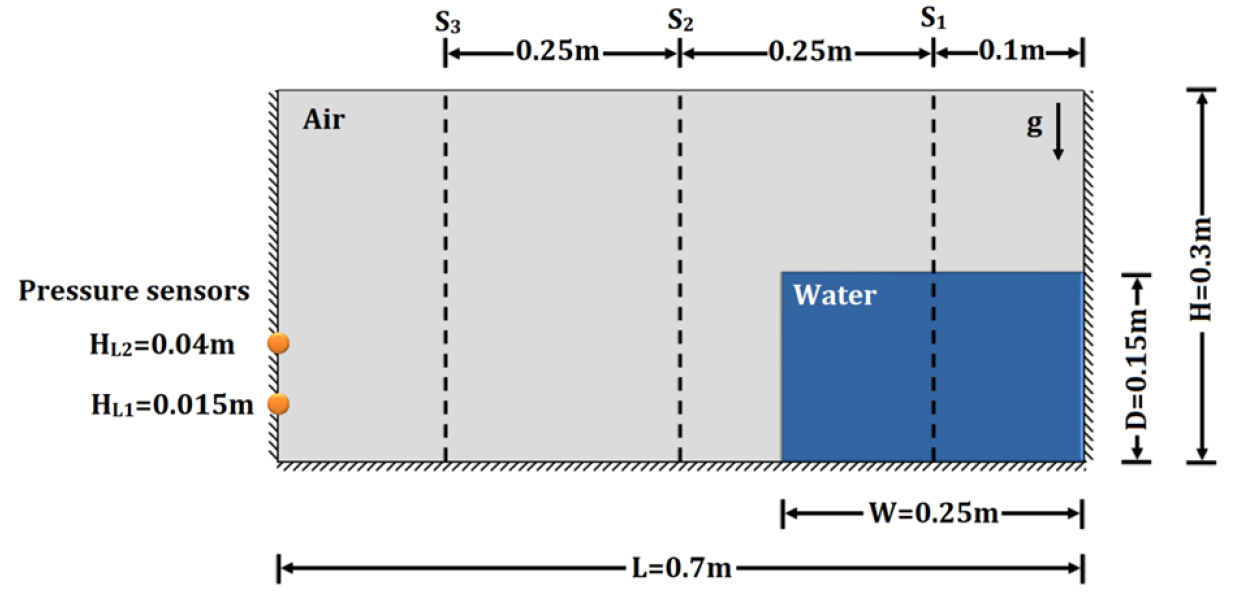
VOF 기법에 적용된 난류모형의 특성을 수면과 유속 변화가 보다 역동적으로 발생하는 흐름에 적용하여 그 특성을 분석하기 위하여 댐 붕괴 흐름에 적용하였다. 모의 조건은 Garoosi et al. (2022)의 실험과 동일하게 설정하여 시간에 따른 자유 수면의 형상과 압력 변화를 비교하였다. Garoosi et al. (2022)은 Fig. 7과 같은 조건에서 순간적으로 수문을 개방하여 총 1 초 동안 댐 붕괴 흐름 양상을 관측하고 $H_{L 1}$ 과 $H_{L 2}$ 지점에 대한 압력 변화를 측정하였다.

본 연구에서는 유체 경계면 해석을 위해 OpenFoam의 interFoam 솔버와 interIsoFoam 솔버를 적용하고 난류 모형은 $k - ω$ SST 모형과 부력 수정 $k - ω$ SST을 적용하여 수치 기법에 따른 흐름 모의 특성을 비교하였다. 수치기법 케이스 구성은 Table 1과 같다. 셀은 길이 방향 640개, 높이 방향 240개로 총 153,600 개의 연직 2차원 형상으로 Fig. 7과 동일한 규모와 초기 조건으로 구성하였다.

Table 1.

Combination of numerical models for dam-break simulation

Numerical model	case1	case2	case3	case4
VOF	interFoam	interFoam	interIsoFoam	interIsoFoam
turbulence model	$k - ω$ SST	buoyance modified $k - ω$ SST	$k - ω$ SST	buoyance modified $k - ω$ SST

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F7.jpg

Fig. 7.

A side views of the experimental setup of the dam-break tests (Garoosi et al., 2022)

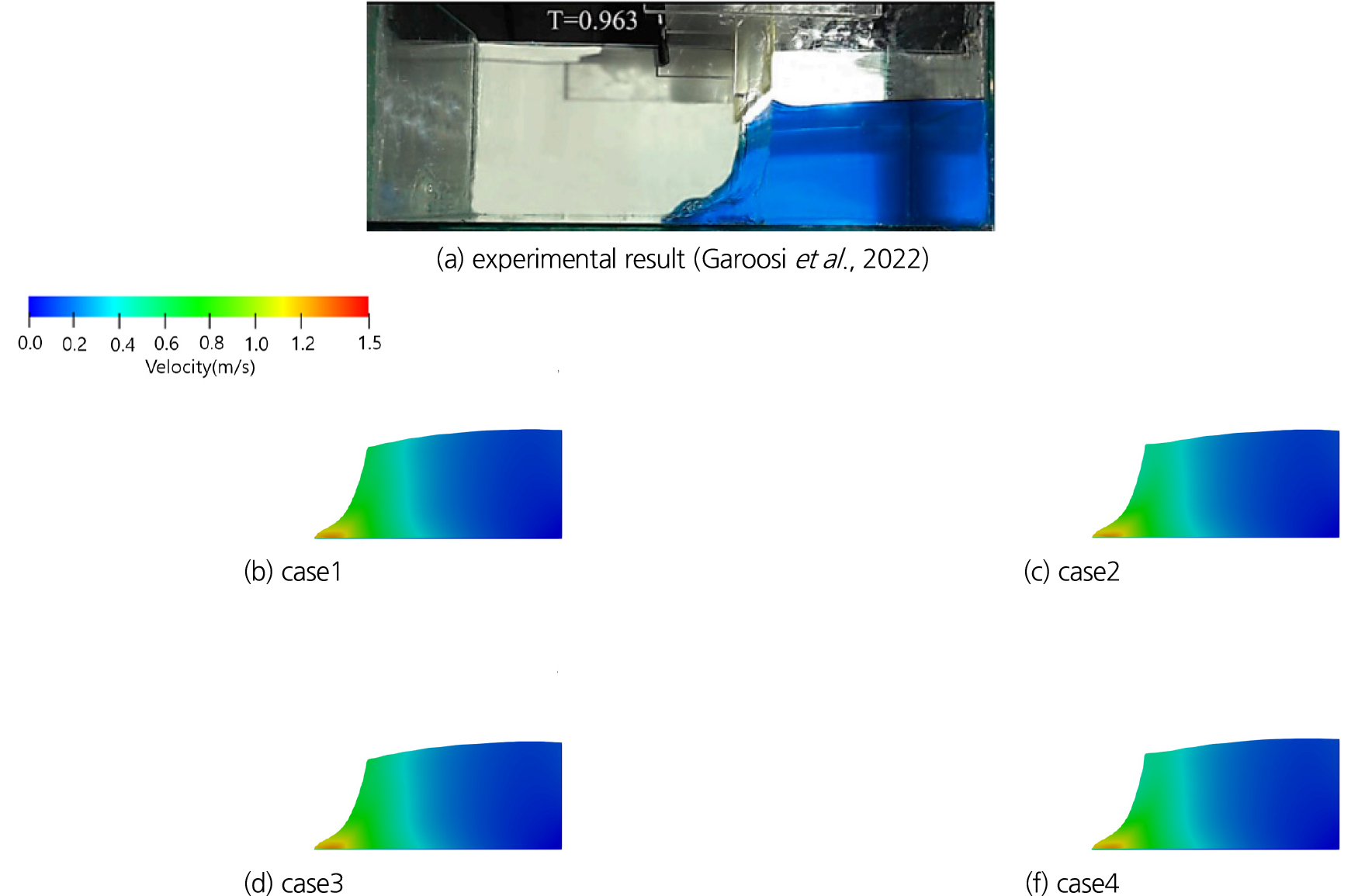
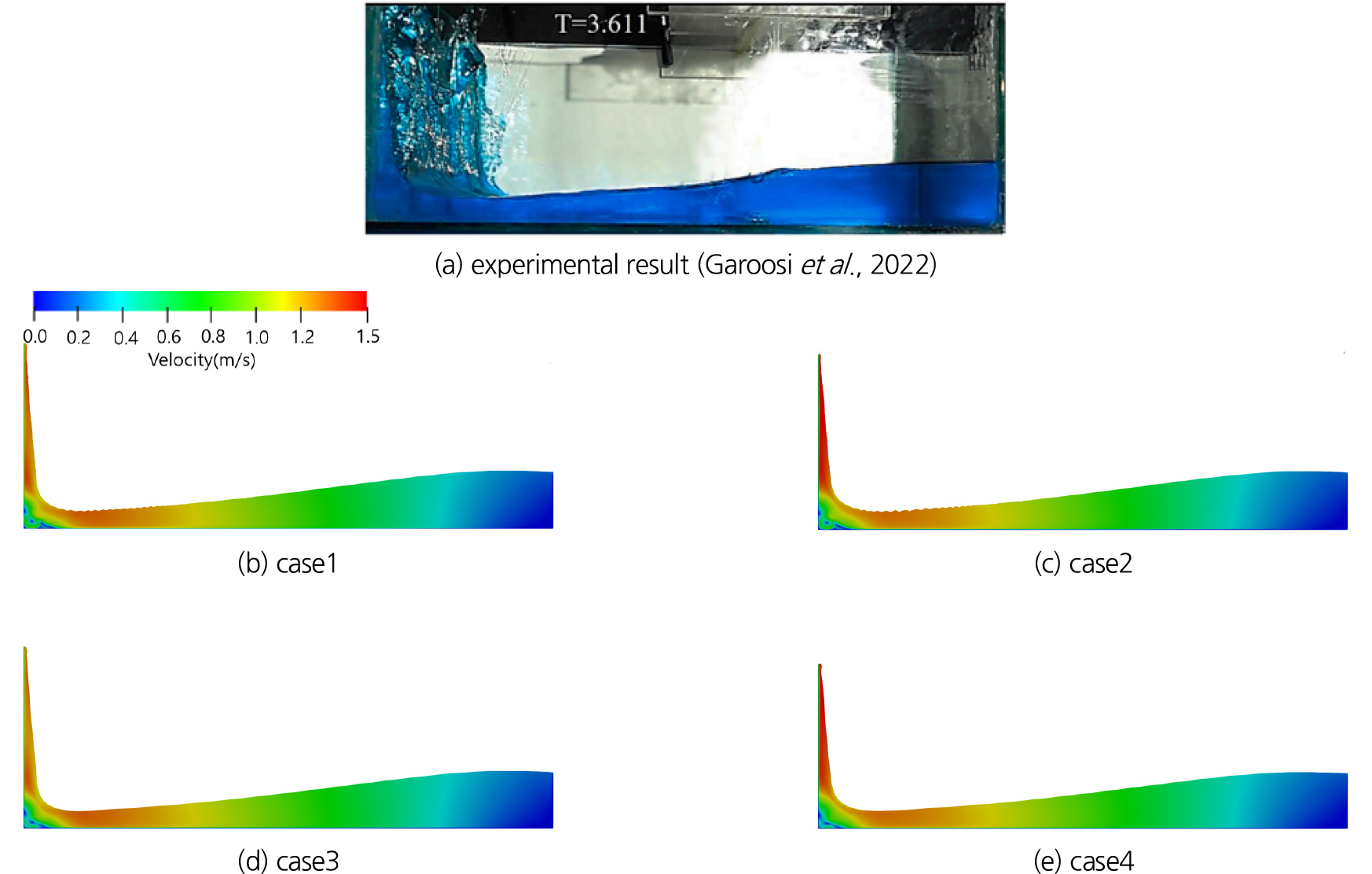
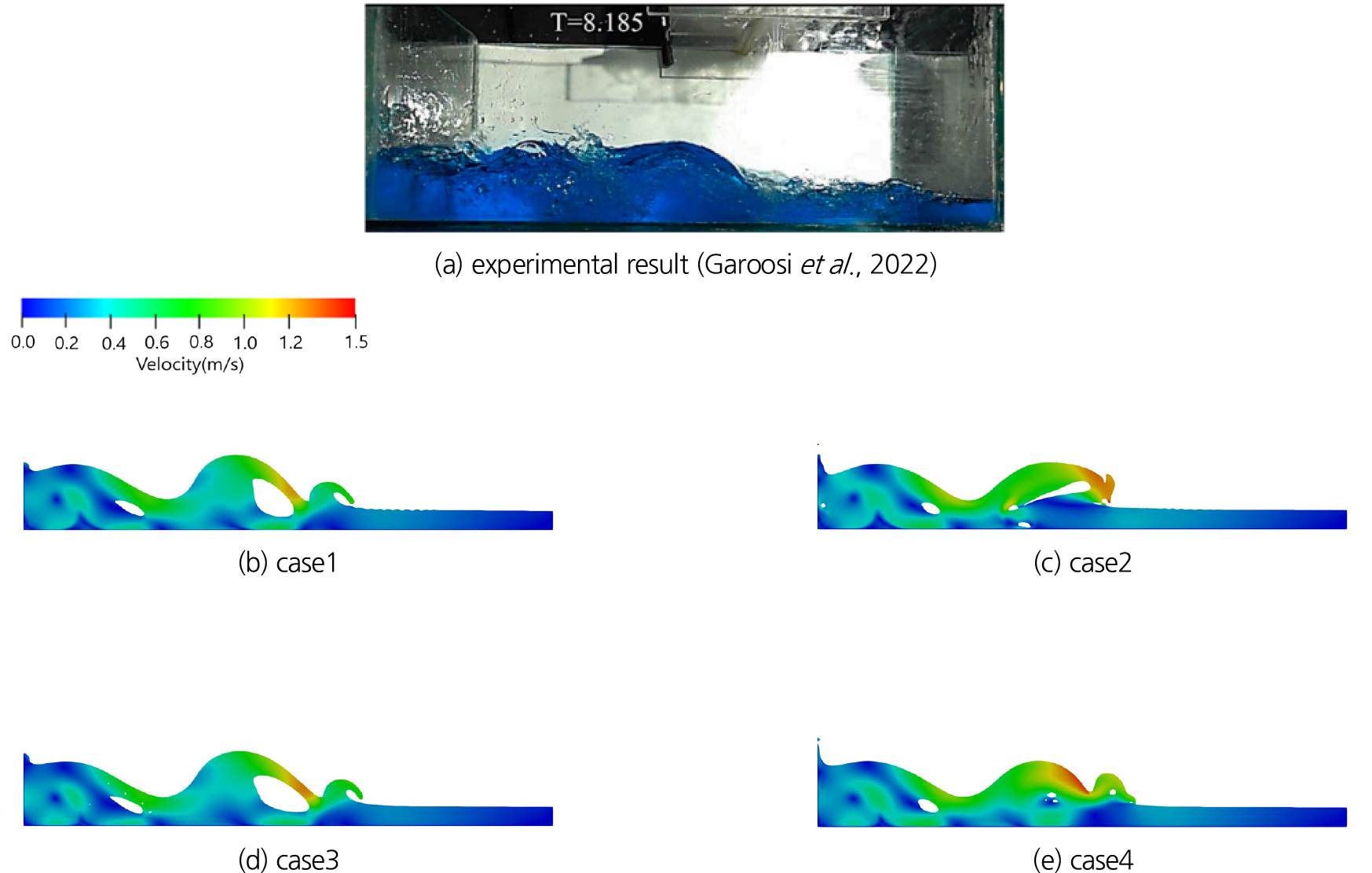
모의 결과를 주요 시간별로 Garoosi et al. (2022)의 실험 결과와 비교하여 제시하며 Figs. 8, 9, 10, 11, 12, 13, 14, 15와 같다. t = 1.0 s 이상에서는 실험결과는 없으나 기법별로 흐름 양상을 비교하기 위하여 같이 제시하였다. 댐 붕괴 흐름 초기인 t = 0.10 s에서는 기법별로 유사한 결과를 보이며 실험과도 유사한 양상을 보인다(Fig. 8). t = 0.45 s에서는 붕괴파가 좌측 벽면에 부딪혀 상승류가 발생하는 단계로 자유수면 형상에서는 기법별로 큰 차이가 없으나 상승류의 유속은 case1과 case2가 유사하고, case3과 case4가 유사한 양상을 보인다. 또한 interFoam 솔버가 적용된 case1과 case2에서는 자유수면에서 진동(wringkle) 현상이 나타나나, interIsoFoam이 적용된 case3와 case4에서는 자유수면의 진동 현상이 나타나지 않는다(Fig. 9).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F8.jpg

Fig. 8.

The time evolutions of free surface profile for dam-break flow at t = 0.10 s

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F9.jpg

Fig. 9.

The time evolutions of free surface profile for dam-break flow at t = 0.45 s

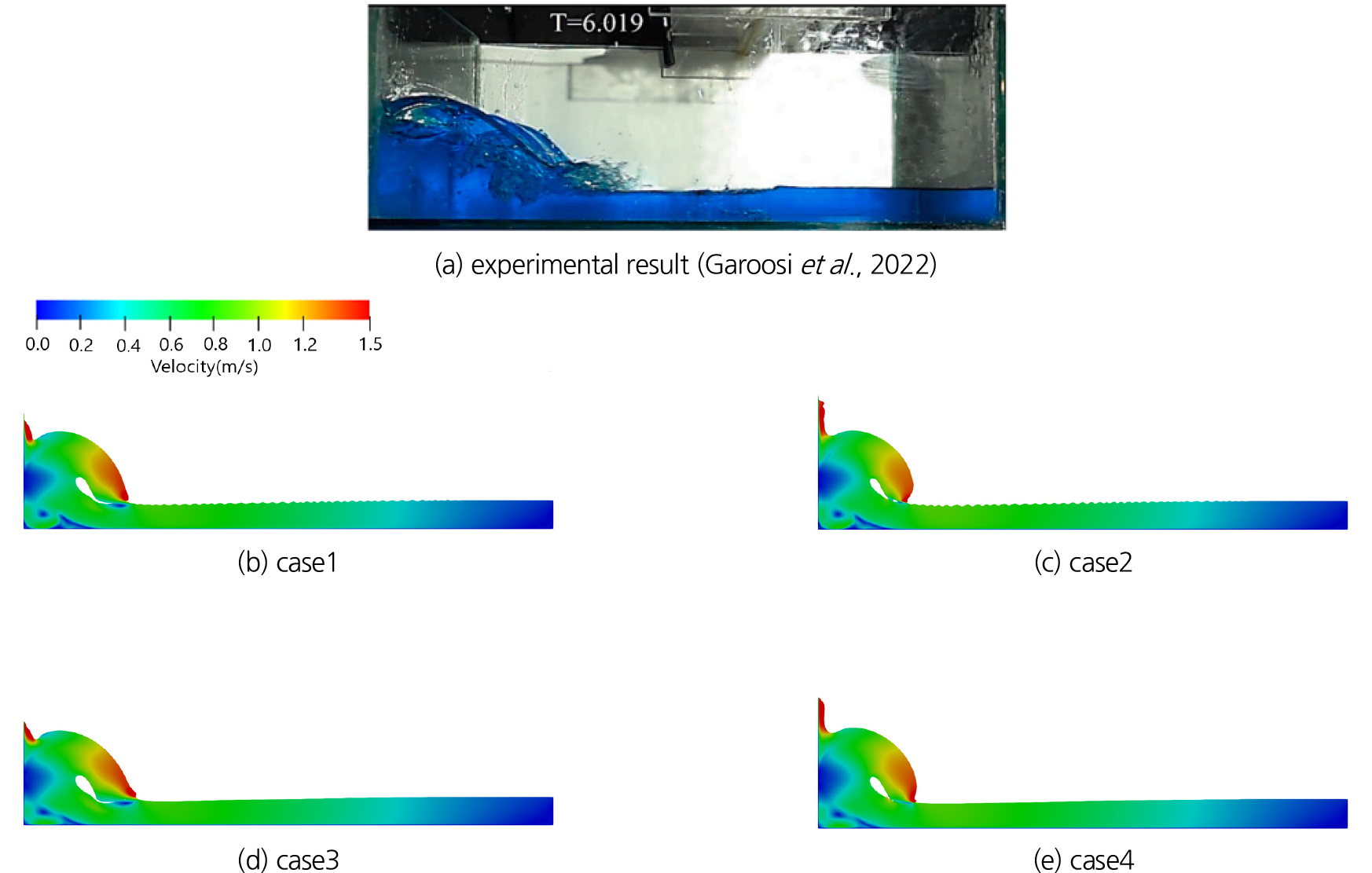
t = 0.75 s는 붕괴파가 왼쪽 벽면에 부딪힌 후 형성된 반사파가 자유수면과 부딪히면서 첫번째 충격이 발생하는 단계인데, 수치기법에 따라 왼쪽에 형성된 반사파가 다소 상이한 양상을 보인다(Fig. 10). 반사파와 내부 공동의 형태는 $k - ω$ SST 모형이 적용된 case1과 case3이 유사하고, 부력 수정 $k - ω$ SST 모형이 적용된 case2와 case4가 유사하게 나타난다. 그러나 왼쪽 아래쪽 코너에 형성된 와류 형태는 case1과 case2가 유사하고, case3과 case4가 유사하게 나타나고 있다. 즉, 특정 영역에 따라 VOF 기법의 영향을 받는 영역과 난류 모형에 영향을 받는 영역이 다소 다름을 확인할 수 있다. 그러나 실험결과와의 비교를 통해 기법 간의 정확성을 판단하기는 어렵다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F10.jpg

Fig. 10.

The time evolutions of free surface profile for dam-break flow at t = 0.75 s

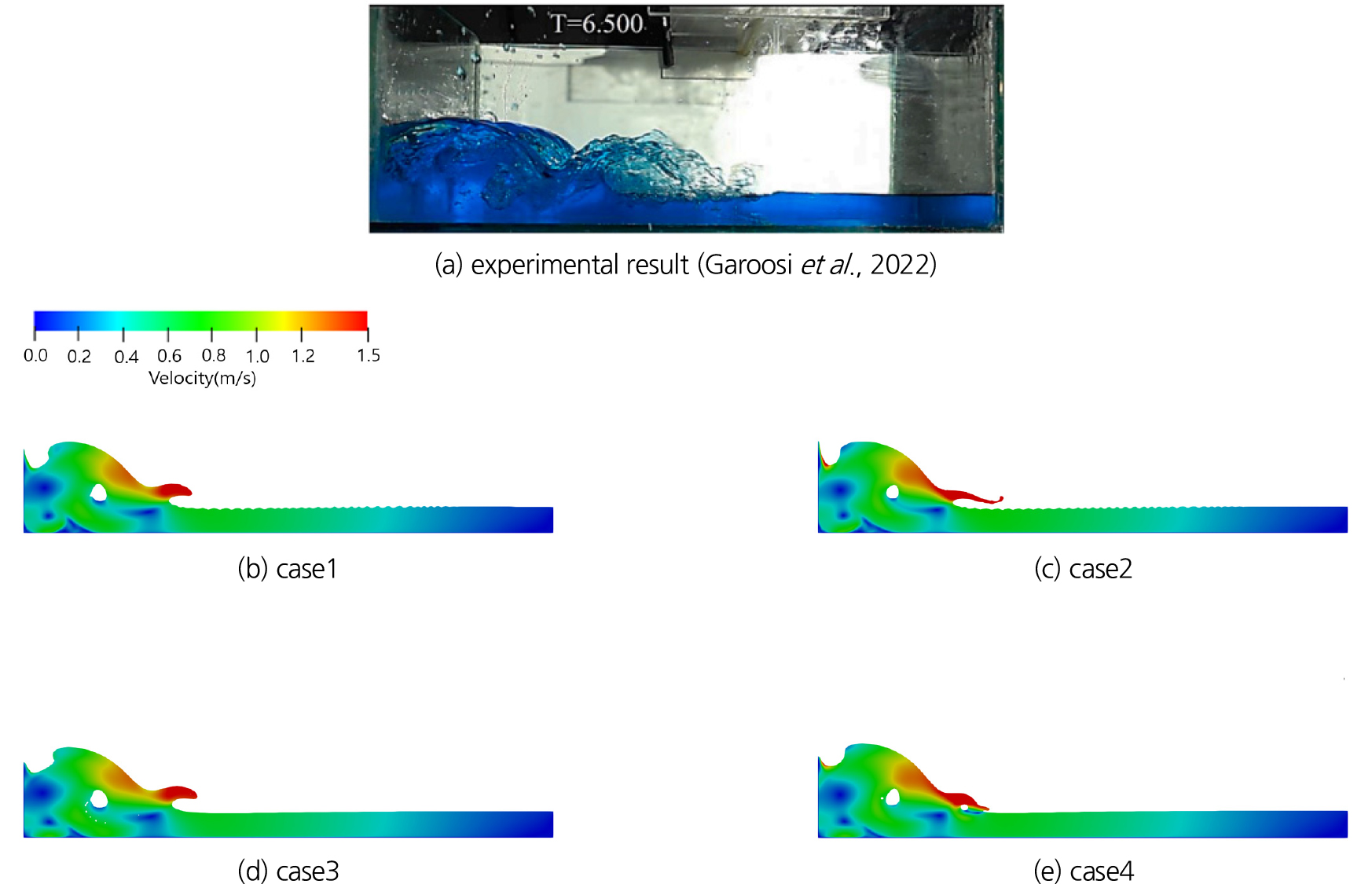
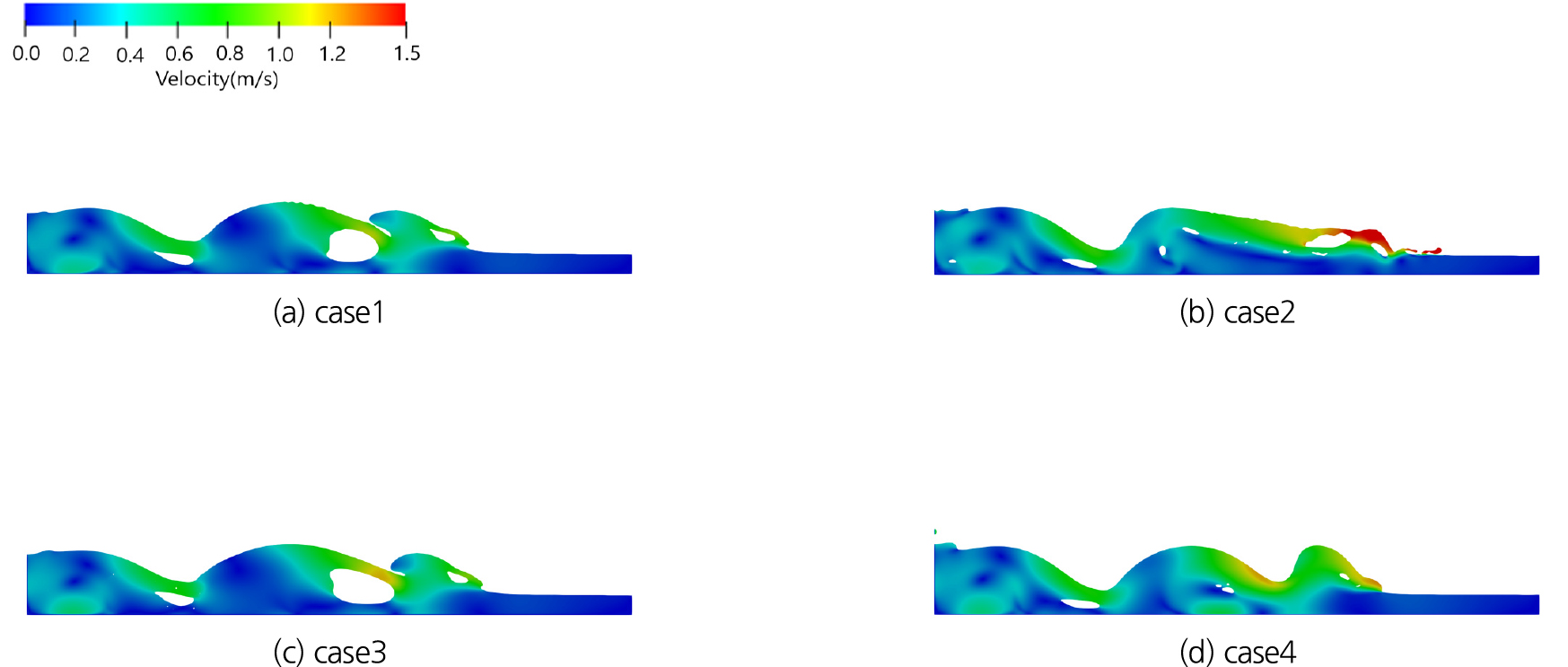
t = 0.80 s는 두번째 반사파가 형성되기 전 단계로 자유수면이 복잡한 양상을 보이는 단계이다(Fig. 11). t = 0.75 s 와 마찬가지로 반사파와 내부 공동의 형태는 $k - ω$ SST 모형이 적용된 case1과 case3이 유사하고, 부력 수정 $k - ω$ SST 모형이 적용된 case2와 case4가 유사하게 나타난다. 또한, 왼쪽 아래쪽 코너에 형성된 와류 형태는 case1과 case2가 유사하고, case3와 case4가 유사하게 나타나고 있다. 그러나 2번째 반사파의 세부적인 형태는 case2와 case4도 다소 다른 발달 양상을 보이고 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F11.jpg

Fig. 11.

The time evolutions of free surface profile for dam-break flow at t = 0.80 s

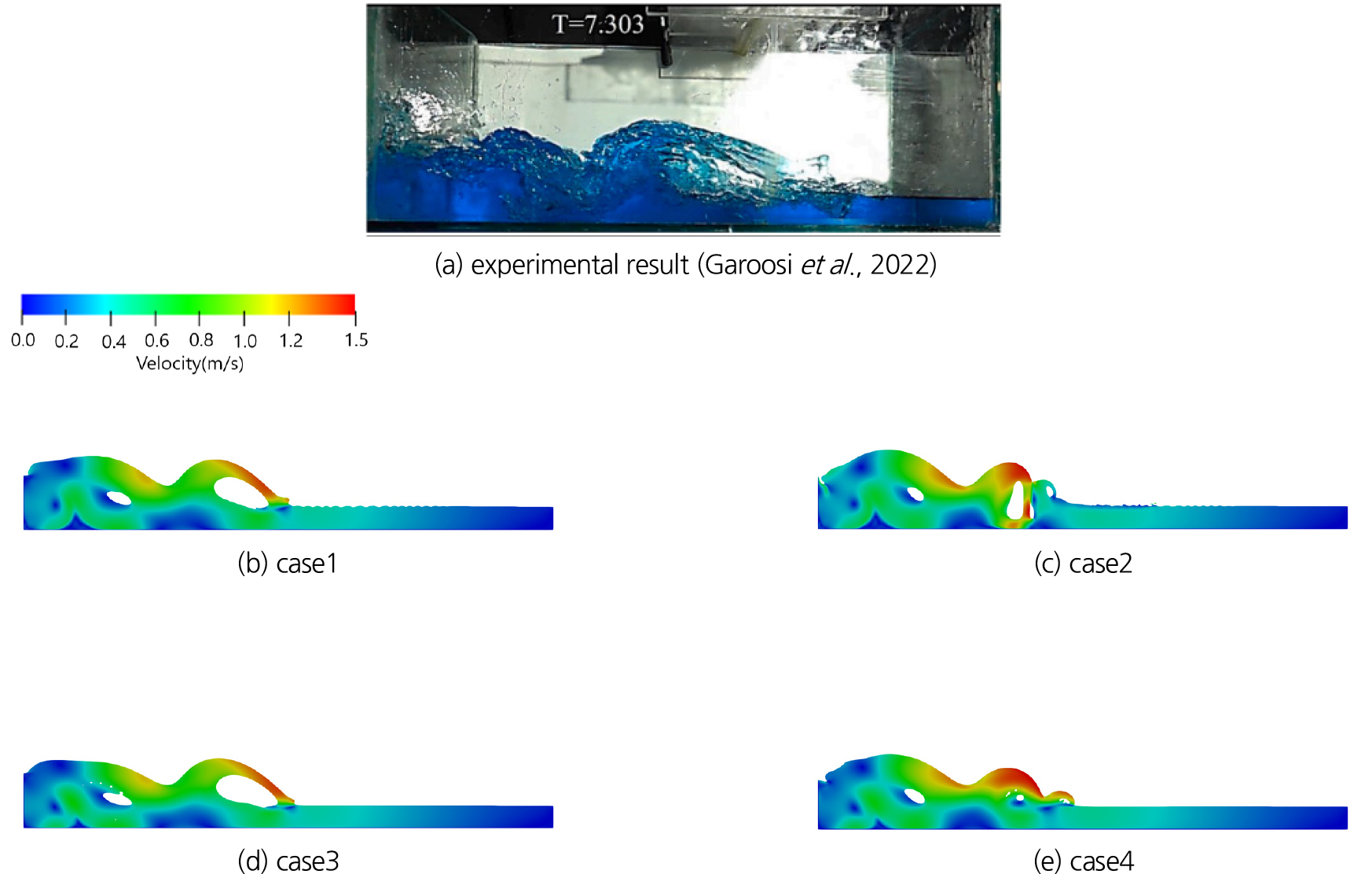
t = 0.90 s는 두번째 반사파가 형성되는 단계로 두번째 반파사 내부의 공동이 크게 형성된다(Fig. 12). 전체적으로 반사파와 내부 공동의 형태는 $k - ω$ SST 모형이 적용된 case1과 case3가 유사하고, 부력 수정 $k - ω$ SST 모형이 적용된 case2와 case4가 유사하게 나타난다. 그러나 두번째 반사파의 세부적인 공동 형태는 case2와 case4가 다른데, case2는 다소 비물리적인 형태의 공동이 나타나며, case4는 공동의 크기가 매우 작게 나타나고 있다. 전체적인 특징은 $k - ω$ SST 모형에 비해 부력 수정 $k - ω$ SST 모형이 2번째 반사파 내부의 공동의 크기를 매우 작게 모의하고 있다. 이 단계에서는 $k - ω$ SST 모형이 실험결과와 유사한 양상을 보이는 것으로 판단된다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F12.jpg

Fig. 12.

The time evolutions of free surface profile for dam-break flow at t = 0.90 s

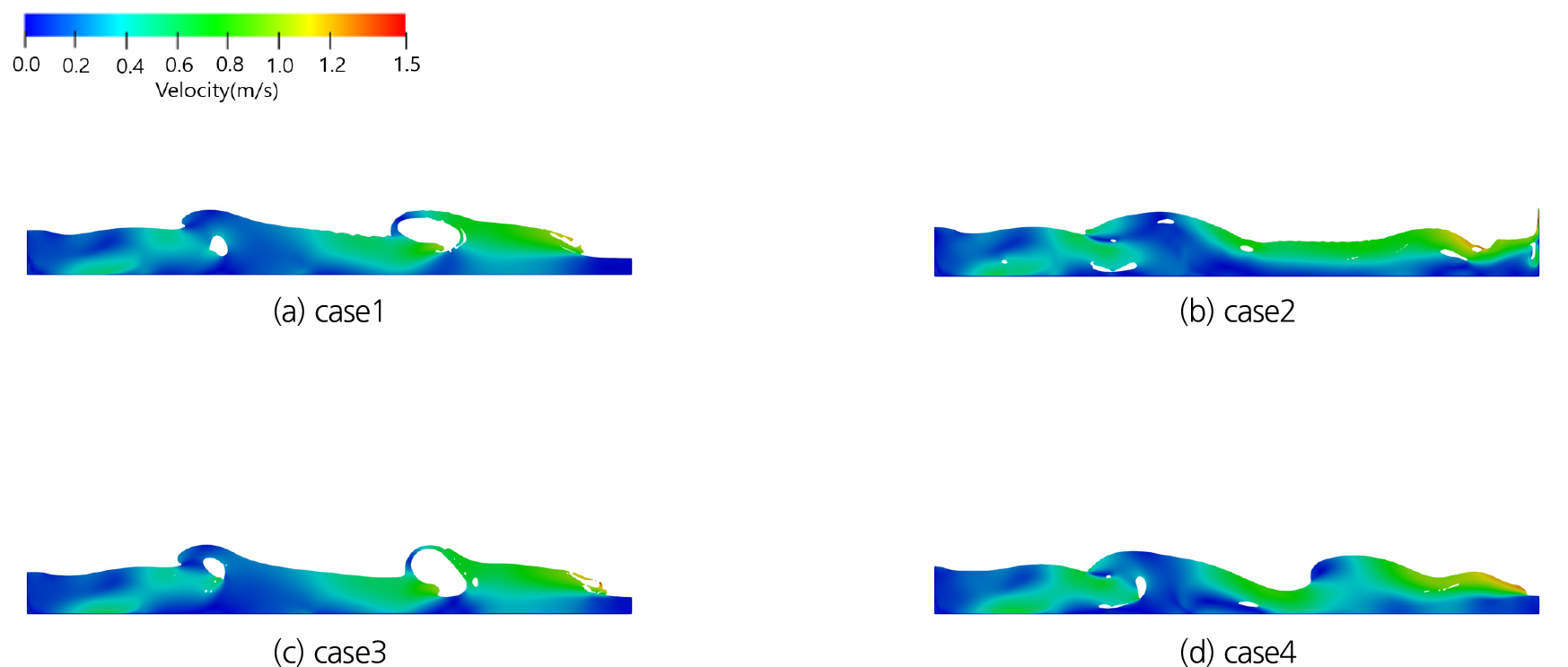
t = 1.00 s에서는 모의 결과 모두 실험결과와는 크게 다른 양상을 보이고 있다(Fig. 13). t = 1.00 s 이후(Figs. 13, 14, 15)의 난류 모형별 특성은 t = 0.90 s와 유사한 경향을 보이고 있다. 즉, $k - ω$ SST 모형이 적용된 case1과 case3가 유사하며, 부력 수정 $k - ω$ SST 모형이 적용된 case2와 case4가 유사하나 구체적인 형태는 차이를 보인다. $k - ω$ SST 모형은 내부 공동을 다소 과도하게 모의하는 것으로 보이며 형성된 공동이 계속 유지되고 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F13.jpg

Fig. 13.

The time evolutions of free surface profile for dam-break flow at t = 1.00 s

반사파에 의해 형성되는 공동 형태는 부력 수정 모형의 특징을 잘 보여주고 있다. 부력 수정 모형이 두번째 반사파로 형성되는 공동의 크기를 작게 모의하는 것은 Fig. 11의 두 번째 공동의 형성 단계에서 그 원인을 유추할 수 있다. $k - ω$ SST 모형은 두 번째 반사파가 형성되는 제트(jet) 흐름의 영역과 각도가 상대적으로 강한 상승류를 형성하나, 부력 수정 $k - ω$ SST 모형은 두번째 반사파의 제트 흐름이 상대적으로 감세된 양상을 보이고 있다. 이로 인해 $k - ω$ SST 모형은 하부층의 물 영역과 제트 흐름 영역의 분리가 상대적으로 강하게 발생하여 보다 큰 공동을 형성한다. 즉, 부력 수정 $k - ω$ SST 모형은 반사파로 인한 제트 흐름을 감세시키는 특성을 보이고 있다. 부력 수정 $k - ω$ SST 모형에 의한 흐름 계산은 부력항 $G_{b}$ 자체가 난류 모형 내에서 음해법으로 계산되므로 흐름에 미치는 영향을 명확하게 파악하는 것은 쉽지 않아, 그 효과는 모의를 통해 확인할 수 밖에 없는 한계를 가진다. 다만, 현단계에서는 다음과 같은 추정이 가능하다. 부력항 $G_{b}$ 는 밀도차가 큰 경계면에서 난류 운동에너지를 층류 수준으로 감세하는 특징을 가지는데, 제트 흐름의 경우에는 흐름 분리로 인해 밀도차가 큰 유체 경계면이 상부와 하부에 동시에 나타나므로 상대적으로 매우 큰 난류 운동에너지 감세가 모의되어 제트 흐름의 감세가 크게 나타나는 것으로 판단된다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F14.jpg

Fig. 14.

The time evolutions of free surface profile for dam-break flow at t = 1.10 s

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F15.jpg

Fig. 15.

The time evolutions of free surface profile for dam-break flow at t = 1.25 s

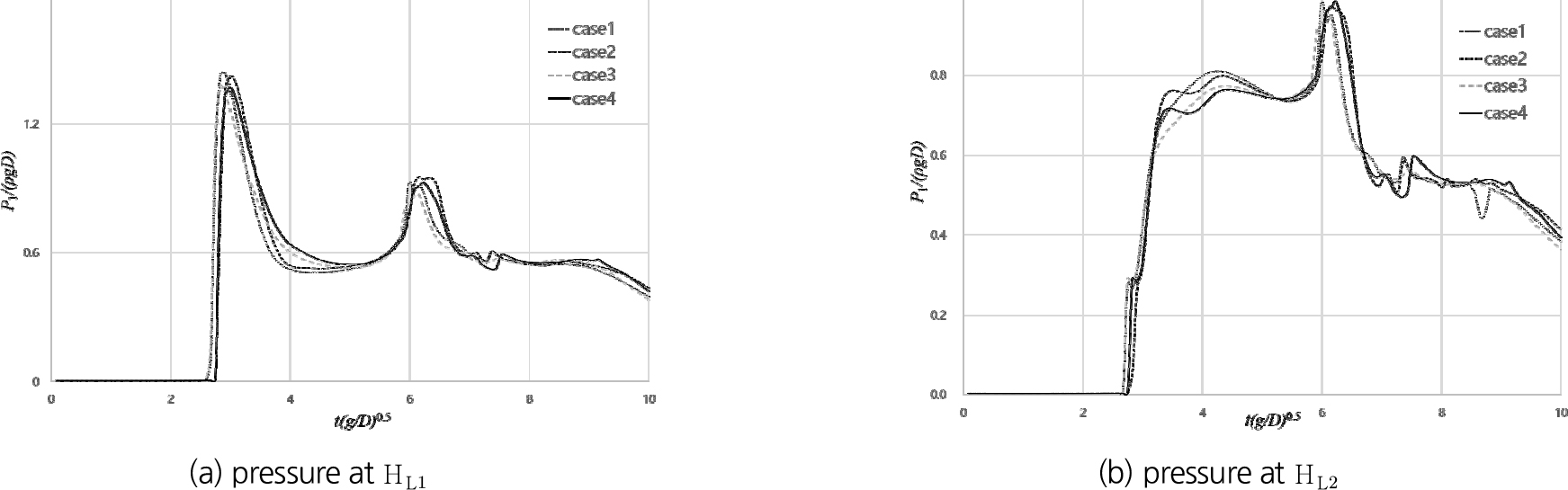
Garoosi et al. (2022)은 댐 붕괴 실험에서 Fig. 7의 두 개 지점( $H_{L 1}$ 과 $H_{L 2}$ )에 대한 무차원 시간에 따른 무차원 압력 측정 결과를 Fig. 16과 같이 제시하였다. 동일 지점에 대해 4개 수치모의 케이스의 압력변화를 도시하면 Fig. 17과 같다. 수치기법에 따라 케이스별로 다소 다른 양상을 나타내나 전체적인 경향은 수치모의 기법별로 유사한 경향을 보인다. 실험결과와 비교하면 $H_{L 1}$ 지점의 경우, 수치모의 결과가 첫번째 및 두번째 압력 피크의 최대 값을 모의하지 못하며 첫번째 압력 피크와 두번째 압력 피크 사이의 압력 변화 양상이 상이하게 모의되고 있다. $H_{L 2}$ 지점의 수치모의 결과도 실험결과와는 다른 양상을 나타내는데, 최대 압력값은 유사하나 증가양상과 감소양상이 크게 상이하게 나타난다. 특히 $H_{L 2}$ 지점에서 최대 압력값 발생 이전 시간의 수치모의 결과는 실험값에 비해 크게 높은 값을 나타내는데, 이 시간은 붕괴파가 좌측 벽면과 충돌 후 상승류가 형성되어 첫 번째 반사파가 형성되기까지의 시점이다. 실험 사진에 의하면 이 시점은 수면에서 공기 혼입에 의한 기포층이 크게 형성되는 단계인데, 수치모의에서는 공기 혼입에 의한 기포층 형성이 모의되지 않으므로 실험에 비해 상대적으로 높은 압력변화가 나타난 것으로 추정된다.

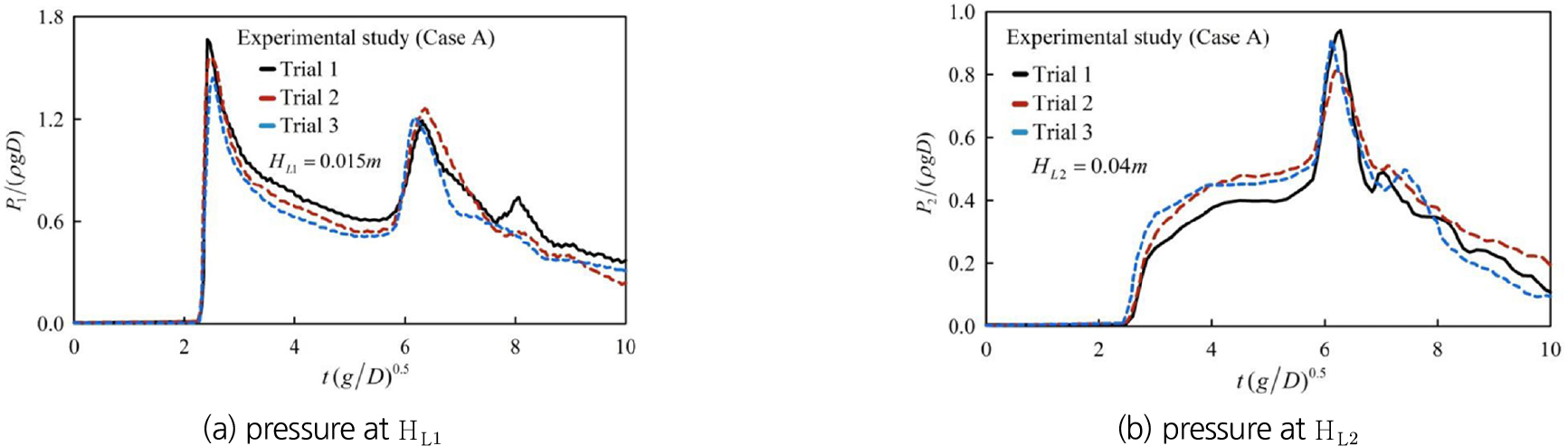
https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F16.jpg

Fig. 16.

The time history of pressure variations at two different sampling points (Garoosi et al., 2022)

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-08/N020057801/images/kwra_57_08_01_F17.jpg

Fig. 17.

The time history of pressure variations at two different sampling points (Simulation results)

4. 요약 및 결론

본 연구에서는 수리분야의 실무 CFD 해석에서 주로 적용되는 VOF 기법 기반의 난류 모형 적용성 평가를 목적으로 수행하였다. VOF 기법 기반으로 기존 난류 모형을 적용하면 자유수면에서 난류 운동에너지를 과도하게 산정하여 비물리적인 거동이 나타는 문제가 오랫동안 제기되어 왔다. 이를 해결하기 위한 대표적인 기법인 Devolder et al. (2018)의 부력 수정 난류 모형을 적용하여 등류 개수로 흐름과 댐 붕괴 흐름에 적용하여 적합성을 평가하였다. 댐 붕괴 흐름 모의 시에는 VOF 기법에 따른 영향도 평가하기 위하여 Weller (2008)가 제안한 가상 압축항 기반 VOF 모형과 Roenby et al. (2016)이 제안한 isoAdvector 기법 기반의 VOF 모형을 함께 적용하였다.

개수로 등류 흐름 조건은 Nezu and Rodi (1986)의 실험과 동일한 조건으로 모의를 수행하였다. 모의 결과에 의하면 기존 $k - ϵ$ 모형과 $k - ω$ SST 모형은 수심에 따라 난류에너지가 증가하는 비물리적인 모의로 인해 수심에 따른 속도 경사가 일반 개수로 흐름의 속도 경사에 비해 급하게 모의되었다. Devolder et al. (2018)가 제안한 부력 수정 난류 모형의 경우 수심에 따른 난류에너지 감소가 관측된 것과 유사하게 모의되었으며 이로 인해 수심에 따른 속도 경사가 일반 개수로 흐름과 유사하게 모의됨을 확인할 수 있었다. 다만, 부력 수정 $k - ϵ$ 모형은 속도 경사를 과도하게 완만하게 모의하는 경향이 있어 부력 수정 $k - ω$ SST 모형이 일반 개수로 흐름의 속도 경사와 유사함을 확인하였다.

자유수면 변화가 역동적으로 발생하는 댐 붕괴 흐름에 VOF 기반의 난류 모형을 적용하여 Garoosi et al. (2022)의 실험과 비교하였다. 모의 결과 댐붕괴파의 1차 반사파는 대체로 유사하게 모의하나, 2차 반사파 형성과 발달은 실험과 다소 큰 차이가 나타났다. 가상 압축항 기반 VOF 모형은 난류 모형과 무관하게 자유수면의 진동이 발생하였다. $k - ω$ SST 모형은 VOF 기법과 무관하게 유사한 모의 결과를 나타내는데 흐름 내의 내부 공동을 과도하게 모의하는 것으로 나타났다. 부력 수정 $k - ω$ SST 모형은 VOF 기법에 따라 2차 반사파 형성 이후 상이한 흐름 발달을 모의하여 VOF 기법에 따른 영향이 있음을 확인하였다. 전체적으로 부력 수정 $k - ω$ SST 모형은 $k - ω$ SST 모형에 비해 반사파 내부 공동을 과소하게 모의하는 경향을 확인할 수 있다. 특히 가상 압축항 기반 VOF 모형과 부력 수정 $k - ω$ SST 모형이 같이 적용된 경우에는 비물리적인 형태의 내부 공동 형성이 나타났다. 지점별 압력 변화 결과는 실험과 유사한 경향을 보이나 정량적인 압력값과 변화 양상은 다소 차이가 나타났다.

본 연구를 통해 RANS 기반으로 이상유체 모의를 위한 실무적인 CFD 해석 기법을 검토하였으며, 최근에 제안된 Devolder et al. (2018)의 부력 수정 난류 모형이 자유수면의 변화가 급격하지 않은 경우에는 비물리적인 난류에너지 분포 문제를 해결하여 개수로 흐름 분포에 적용성이 있다고 판단된다. 그러나, 자유 수면의 급격한 변화가 발생하는 경우에도 범용적으로 적용하기에는 한계가 있는 것으로 보인다. 개수로 흐름의 실무적인 CFD 해석시에는 흐름 특성에 따라 난류 모형을 적절하게 보정하는 것이 여전히 필요할 것으로 판단된다. 또한, 자유 수면의 급격한 변화로 인한 공기 혼입을 고려하기 위한 연구가 필요할 것으로 판단된다.

Acknowledgements

본 연구는 한국건설기술연구원 2024년도 목적형 목적형 R&R 사업 ‘기후위기 대응 물문제 해결형 이슈 발굴 및 미래선도 기술 개발(20240128-001)’의 일환으로 수행되었습니다.

Conflicts of Interest

The authors declare no conflict of interest.

References

ANSYS Fluent (2016). ANSYS Fluent theory guide. PA, U.S.

Bradford, S.F. (2000). "Numerical simulation of surf zone dynamics." Journal of Waterway, Port, Coastal, and Ocean Engineering, Vol. 126, No. 1, pp. 1-13. doi: 10.1061/(ASCE)0733-950X(2000)126:1(1).

10.1061/(ASCE)0733-950X(2000)126:1(1)

Brown, S.A., Greaves, D.M., Magar, V., and Conley, D.C. (2016). "Evaluation of turbulence closure models under spilling and plunging breakers in the surf zone." Coastal Engineering, Vol. 114, pp. 177-193. doi: 10.1016/j.coastaleng.2016.04.002.

10.1016/j.coastaleng.2016.04.002

Christensen, E.D. (2006). "Large eddy simulation of spilling and plunging breakers." Coastal Engineering, Vol. 53, No. 5-6, pp. 463-485. doi: 10.1016/j.coastaleng.2005.11.001.

10.1016/j.coastaleng.2005.11.001

Deshpande, S.S., Anumolu, L., and Trujillo, M.F. (2012). "Evaluating the performance of the two-phase flow solver interFoam." Computational Science & Discovery, IOP Publishing Ltd, Vol. 5, No. 1, 014016.

10.1088/1749-4699/5/1/014016

Devolder, B., Troch, P., and Rauwoens, P. (2018). "Performance of a buoyancy-modified k-ω and k-ω SST turbulence model for simulating wave breaking under regular waves using OpenFOAM®." Coastal Engineering, Vol. 138, pp. 49-65.

10.1016/j.coastaleng.2018.04.011

Egorov, Y., Boucker, M., Martin, A., Pigny, S., Scheuerer, M., and Willemsen, S. (2004). "Validation of CFD codes with PTS- relevant test cases." 5th Euratom Framework Programme ECORA Project 2004, pp. 91-116.

Fernandez-Mora, A., Ribberink, J.S., van der Zanden, J., van der Werf, J.J., and Jacobsen, N.G. (2017). "RANS-VOF modeling of hydrodynamics and sand transport under full-scale non-breaking and breaking waves." Proceedings of 35th Conference on Coastal Engineering, Antalya, Turkey, pp. 1-15. doi: 10.9753/ICCE.V35.SEDIMENT.29.

10.9753/icce.v35.sediment.29

Frederix, E.M.A., Mathur, A., Dovizio, D., Geurts, B.J., and Komen, E.M.J. (2018). "Reynolds-averaged modeling of turbulence damping near a large-scale interface in two-phase flow." Nuclear Engineering and Design, Vol. 333, pp. 122-130. doi: 10.1016/j.nucengdes.2018.04.010.

10.1016/j.nucengdes.2018.04.010

Garoosi, F., Mellado-Cusicahua, A.N., Shademani, M., and Shakibaeinia, A. (2022). "Experimental and numerical investigations of dam break flow over dry and wet beds." International Journal of Mechanical Sciences, Vol. 215, 106946. doi: 10.1016/j. ijmecsci.2021.106946.

10.1016/j.ijmecsci.2021.106946

Guo, J., Julien, P.Y., and Meroney, R.N. (2005). "Modified Log-wake law in Zero-pressure-gradient turbulent boundary layers." Journal of Hydraulic Research, IAHR, Vol. 43, No. 4, pp. 421-430.

10.1080/00221680509500138

Hirt, C.W., and Nichols, B.D. (1981). "Volume of fluid (VoF) method for the dynamics of free boundaries." Journal of Computational Physics, Vol. 39, No. 1, pp. 201-225. doi: 10.1016/0021-9991(81)90145-5.

10.1016/0021-9991(81)90145-5

Hoang, D.A., van Steijn, V., Portela, L.M., Kreutzer, M.T., Kleijn, C.R. (2013). "Benchmark numerical simulations of segmented two-phase flows in microchannels using the Volume of Fluid method." Computers & Fluids, Vol. 86, pp. 28-36. doi: 10.1016/j.compfluid.2013.06.024.

10.1016/j.compfluid.2013.06.024

Jacobsen, N.G., Fredsoe, J., and Jensen, J.H. (2014). "Formation and development of a breaker bar under regular waves. Part 1: Model description and hydrodynamics." Coastal Engineering, Vol. 88, pp. 182-193. doi: 10.1016/j.coastaleng.2013.12.008.

10.1016/j.coastaleng.2013.12.008

Kamath, A., Gábor F., and Hans B. (2019). "Investigation of free surface turbulence damping in RANS simulations for complex free surface flows." Water, Vol. 11, No. 3, 456. doi: 10.3390/w11030456.

10.3390/w11030456

Marschall, H., Hinterberger, K., Schüler, C., Habla, F., and Hinrichsen, O. (2012). "Numerical simulation of species transfer across fluid interfaces in free-surface flows using OpenFOAM." Chemical Engineering Science, Vol. 78, pp. 111-127. doi: 10.1016/j.ces.2012.02.034.

10.1016/j.ces.2012.02.034

Mayer, S., and Madsen, P.A. (2001). "Simulation of breaking waves in the surf zone using a Navier-Stokes solver." Coastal Engineering 2000, ASCE, Sydney, Australia, pp. 928-941. https://doi.org/10.1061/40549(276)72.

10.1061/40549(276)7211514381

Menter, F.R. (1994). "Two-equation eddy-viscosity turbulence models for engineering applications." AIAA Journal, Vol. 32, No 8. pp. 1598-1605.

10.2514/3.12149

Mukha, T., Almeland, S.K., and Bensow, R.E. (2022). "Large-eddy simulation of a classical hydraulic jump: Influence of modelling parameters on the predictive accuracy." Fluids 2022, Vol. 7, No. 3, 101.

10.3390/fluids7030101

Nezu, I., and Rodi, W. (1986). "Open-channel flow measurements with a laser doppler anemometer." Journal of Hydraulic Engineering, Vol. 112, No. 5, pp. 335-355.

10.1061/(ASCE)0733-9429(1986)112:5(335)

Raeini, A.Q., Blunt, M.J., and Bijeljic, B. (2012). "Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method." Journal of Computational Physics, Vol. 231, No. 17, pp. 5653-5668, doi: 10.1016/j.jcp.2012.04.011.

10.1016/j.jcp.2012.04.011

Roenby, J., Bredmose, H., and Jasak, H. (2016). "A computational method for sharp interface advection." Royal Society Open Science, Vol. 3, No. 11, 160405.

10.1098/rsos.16040528018619PMC5180117

Roenby, J., Larsen, B.E., Bredmose, H., and Jasak H. (2017). "A new volume-of-fluid method in OpenFOAM." VII International Conference on Computational Methods in Marine Engineering, Rome, Italy.

Weller, H. (2008). A new approach to VOF-based interface capturing methods for incompressible and compressible flows. Report TR/HGW/04, OpenCFD Ltd., MA, U.S.

Xie, Z. (2013). "Two-phase flow modelling of spilling and plunging breaking waves." Applied Mathematical Modelling, Vol. 37, No. 6, pp. 3698-3713. doi: 10.1016/j.apm.2012.07.057.

10.1016/j.apm.2012.07.057

Xie, Z., Lin, B., Falconer, R.A., Nichols, A., Tait, S.J., and Horoshenkov, K.V. (2022). "Large-eddy simulation of turbulent free surface flow over a gravel bed." Journal of Hydraulic Research, Vol. 60, No. 2, pp. 205-219. doi: 10.1080/00221686.2021.1908437.

10.1080/00221686.2021.1908437

Zhou, Z., Hsu, T.J., Cox, D., Liu, X. (2017). "Large-eddy simulation of wave-breaking induced turbulent coherent structures and suspended sediment transport on a barred beach." Journal of Geophysical Research: Oceans, Vol. 122, No. 1, pp. 207-235. doi: 10.1002/2016JC011884.

10.1002/2016JC011884

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Evaluation of the applicability of a buoyancy-modified turbulence model for free surface flow analysis based on the VOF method

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

Fig. 1.

The grid composition for unifrom flow

Fig. 2.

Velocity profiles of Nezu and Rodi expriments (Nezu and Rodi, 1986)

Fig. 3.

Turbulence intensity of Nezu and Rodi expriments (Nezu and Rodi, 1986)

Fig. 4.

Velocity profiles of uniform flow condition in y+ and u+

Fig. 5.

Velocity profile comparisons with modified log-wake law

Fig. 6.

Turbulence intensity of selected turbulence models

Table 1.

Combination of numerical models for dam-break simulation

Fig. 7.

A side views of the experimental setup of the dam-break tests (Garoosi et al., 2022)

Fig. 8.

The time evolutions of free surface profile for dam-break flow at t = 0.10 s

Fig. 9.

The time evolutions of free surface profile for dam-break flow at t = 0.45 s

Fig. 10.

The time evolutions of free surface profile for dam-break flow at t = 0.75 s

Fig. 11.

The time evolutions of free surface profile for dam-break flow at t = 0.80 s

Fig. 12.

The time evolutions of free surface profile for dam-break flow at t = 0.90 s

Fig. 13.

The time evolutions of free surface profile for dam-break flow at t = 1.00 s

Fig. 14.

The time evolutions of free surface profile for dam-break flow at t = 1.10 s

Fig. 15.

The time evolutions of free surface profile for dam-break flow at t = 1.25 s

Fig. 16.

The time history of pressure variations at two different sampling points (Garoosi et al., 2022)

Fig. 17.

The time history of pressure variations at two different sampling points (Simulation results)

Acknowledgements

Conflicts of Interest

References

Velocity profiles of uniform flow condition in $y^{+}$ and $u^{+}$