Development of the Bayesian method and its application to the water resources field

Wooyoung Na; Chulsang Yoo

doi:10.3741/JKWRA.2021.54.1.1

Preview

Review Article

Journal of Korea Water Resources Association. 31 January 2021. 1-13
https://doi.org/10.3741/JKWRA.2021.54.1.1

Development of the Bayesian method and its application to the water resources field

베이지안 기법의 발전 및 수자원 분야에의 적용

Wooyoung Na^a

Chulsang Yoo^b^†

나 우영^a

유 철상^b^†

^aPh.D Candidate, School of Civil, Environmental and Architectural Engineering, Korea University, Seoul, Korea

^bProfessor, School of Civil, Environmental and Architectural Engineering, Korea University, Seoul, Korea

^a고려대학교 공과대학 건축사회환경공학과 박사과정

^b고려대학교 공과대학 건축사회환경공학부 교수

^*envchul@korea.ac.kr

ABSTRACT

The Bayesian method is a very useful statistical tool in various fields including water resources. Therefore, in this study, the background of the Bayesian statistics and its application to the water resources field are reviewed. First, the history of the Bayesian method from the birth to the present, and the achievements of Bayesian statisticians are summarized. Next, the derivation of the Bayes’ theorem, which is the basis of the Bayesian method, is presented, and the roles of the three elements of the Bayes’ theorem: priori distribution, likelihood function, and posteriori distribution are explained. In addition, the unique features and advantages of the Bayesian statistics are summarized. Finally, the cases in water resources where the Bayesian method is applied are summarized by dividing them into several categories. With a prevalence of information and big data in the future, the Bayesian method is expected to be used more actively in the water resources field.

Keywords

Bayesian statistics

Bayesian method

Bayes’ theorem

베이지안 기법은 수자원을 포함한 다양한 분야에서 매우 유용한 통계적 도구로 이용되고 있다. 이에 본 연구에서는 베이지안 통계학에 대해 그 배경을 고찰하고, 수자원 분야에 적용된 사례를 소개하였다. 먼저, 베이지안 통계학의 탄생에서부터 현재에 이르기까지의 발전 과정과 이에 기여한 베이지안 통계학자들의 업적 등을 정리하였다. 다음으로 베이지안 기법의 근간이 되는 베이즈 정리의 유도 과정을 제시하고, 베이즈 정리의 세 요소인 사전분포, 우도함수, 사후분포의 역할에 대해 설명하였다. 또한, 베이지안 통계학이 가지는 고유한 특징과 장점에 대해 정리하였다. 마지막으로 수자원 분야에 베이지안 기법이 적용된 사례를 여러 범주로 나누어 정리하였다. 베이지안 기법은 정보 및 빅데이터의 활용이 커짐에 따라 수자원 분야에서 더욱 유용하게 적용될 것으로 전망된다.

키워드

베이지안 통계학

베이지안 기법

베이즈 정리

MAIN

1. 서 론
2. 베이지안 통계학의 발전 과정
3. 베이즈 정리 및 베이지안 통계학의 특징
3.1 베이즈 정리
3.2 베이즈 정리의 유도
3.3 베이지안 통계학의 특징
4. 수자원 분야의 베이지안 기법 적용 사례
4.1 정보의 결합
4.2 모형의 결합: 앙상블 개념
4.3 통계적 추론: 매개변수 추정
4.4 불확실성 정량화
4.5 응용기법 및 기타 적용 사례
5. 결 론

1. 서 론

베이지안 통계학은 현재 다양한 분야에서 이용되고 있는 통계학의 한 분야이다. 특히 최근 데이터의 대용량화, 자료 형태의 다양화, 통계학의 실용화로 인해 베이지안 통계학의 영향력이 더더욱 커지고 있다. 통계학뿐만 아니라 경영학, 정치학, 의학, 생물학, 공학, 기상학 등 다양한 학문 분야에서도 베이지안 통계학을 접목시키는 사례가 늘고 있는 추세이다(Berger, 2000). 또한, 구글, 마이크로소프트와 같은 디지털 정보화 시대를 선도하는 기업들에서 베이지안 통계학에 주목하고 있다(Di et al., 2014; Prochazka et al., 2015). 스팸메일 필터링, 연관 검색 키워드 제공 등 베이지안 통계학이 실생활에 적용되는 사례 또한 점점 증가하고 있다. 이렇듯 베이지안 통계학은 최근 상당한 주목을 받고 있으며, 그 우수성이 검증되고 있다.

수자원 분야에서도 베이지안 통계학은 상당히 유용한 확률통계학적 도구로 자리매김하고 있다. Web of Science 검색 엔진을 이용하여 “Bayesian Water Resources”라는 키워드로 게재된 연간 논문 수를 분석한 결과, 2008년 이전에는 20개 이하였다가 2013년부터는 50개 이상이 되었으며, 그 이후로 지속적으로 증가하는 추세이다. 이는 수자원 관련 분야의 연구에 베이지안 통계학의 활용도가 점점 커지고 있다는 점을 시사한다. 베이지안 통계학은 자료의 시공간적 확장, 극치 자료에 대한 해석, 수문모형의 매개변수 추정, 시계열 예측, 이수 측면에서의 의사결정 등과 같은 다양한 문제들에 적용되고 있다(Insua et al., 2002). 최근에는 기계학습, 인공지능과 관련된 컴퓨터과학 기술이 발전함에 따라 베이지안 네트워크, 베이지안 신경망, 베이지안 필터 등 응용기법들이 등장하여 수자원 분야에서 활발히 적용되고 있다(Khan and Coulibaly, 2010; Chan et al., 2012; Ait-El-Fquih et al., 2016).

본 연구의 목적은 최근 활용성이 증대되고 있는 베이지안 통계학에 대해 그 배경을 고찰하고, 특히 수자원 분야에 적용된 사례를 소개하는 데 있다. 본 연구는 다음과 같은 내용으로 구성된다. 먼저, 2장에서는 약 250년의 긴 역사를 가진 베이지안 통계학이 현재까지 어떠한 과정을 거쳐 발전해왔는지에 대해 정리하였다. 3장은 베이지안 통계학의 기저에 있는 베이즈 정리와 베이지안 통계학의 장점 및 특징에 관한 내용이다. 베이즈 정리를 유도하고, 베이즈 정리를 구성하는 세 가지 요소인 사전분포, 우도함수, 사후분포에 대해 설명하였다. 마지막으로 4장에서는 베이지안 기법이 수자원 분야에 적용된 다양한 사례를 소개하였다. 정보 및 모형의 결합, 모형의 매개변수 추정, 불확실성 정량화를 위해 베이지안 기법이 어떠한 방식으로 적용되었는지, 그리고 베이지안 기법을 활용한 기타 응용기법 등에 대해 서술하였다.

2. 베이지안 통계학의 발전 과정

베이지안 통계학은 지금으로부터 약 250년 전, 베이즈 이론을 고안해낸 영국의 목사 Thomas Bayes의 이름을 딴 통계학의 한 범주이다. Fienberg (2006)와 McGrayne (2011), Lee et al. (2014)를 살펴보면 베이지안 통계학의 역사를 상세히 확인할 수 있다. 먼저, Bayes의 이론은 그가 사망한 이후인 1763년, 그의 동료인 Richard Price에 의해 세상에 알려지게 되었다. Bayes는 “관찰 결과로부터 그 결과를 유발한 가장 그럴듯한 원인은 무엇인가”라는 문제에 관심을 가졌다. 이러한 사고는 당시로서는 매우 생소한 것이었으며, 이 질문에 대한 답을 찾고자 Bayes는 테이블에 떨어진 공이 정지하는 위치를 추론하는 사고실험(thought experiment)을 하였다. 추론의 대상은 첫 번째 공이 정지한 위치이며, 다른 공을 계속 떨어뜨리면 최초 공 위치의 오른쪽 혹은 왼쪽이라는 새로운 결과가 발생한다. 매 시행마다 발생하는 추가적인 정보에 의해 최초로 떨어진 공의 위치에 대한 추론이 지속적으로 개선된다는 개념을 바탕으로 베이즈 이론이 탄생하게 되었다. 그러나 Bayes는 본인의 이론이 불완전하다고 생각했기 때문에 논문이 아닌 메모의 형태로 남겨놓았으며, 수식을 제시하지도 않았다.

베이즈 정리를 현재 우리에게 익숙한 베이즈 정리의 형태로 만든 사람은 프랑스의 학자 Pierre-Simon Laplace이다. Laplace가 제시한 최초의 베이즈 정리는 Eq. (1)과 같다.

(1)

P (C | E) = \frac{P (E | C) P_{p r i o r} (C)}{\sum_{} P (E | C) P_{p r i o r} (C)}

여기서 P(C | E)는 어떤 결과 E를 유발한 특정한 원인 C의 확률이고, P(E | C)는 가능성 있는 원인 C에 대한 결과 E의 발생 확률을 의미한다. P_prior (C)는 원인에 대한 최초의 추정치이다. 분모는 가능한 모든 원인들에 대한 확률을 합한 것과 같다. Laplace는 사건을 유발한 원인에 대한 사전정보가 적거나 없는 경우에 모든 원인에 동등한 확률을 부여해도 된다는 “이유 불충분의 원칙(principle of indifference)”을 주장했기 때문에 P_prior (C)를 생략하는 경우가 더 많았다.

1800년대 말 빈도론적 통계학(Frequentist Statistics)이 등장하면서 베이지안 통계학은 침체기를 겪었다. 대부분의 빈도론적 통계학자들은 베이지안 통계학자들이 주장하는 “주관적 확률” 개념을 강력히 비판하였다. 이들은 확률은 특정한 사건에 대한 주관적인 믿음의 정도가 아닌 그 사건이 과거에 발생한 빈도를 의미한다고 주장하였다. 특히 영국의 통계학자인 Ronald Fisher는 빈도론적 통계학의 선두 주자로써 “무작위 방법론(randomization method)”을 토대로 샘플링 이론, 유의성 검정, 최우도법 등을 제시하였고, 베이지안 통계학을 “도무지 발을 들여놓을 수 없는 정글”이라는 말로 비난하였다. 그 다음 세대의 미국 수학자 Jerzy Neyman 또한 반(反)베이즈주의자였으며, 무작위적인 반복 추출이 가능한 문제들만 연구 대상으로 삼고 표본을 유일한 정보의 원천으로 여겼다. 이러한 분위기 속에서도 영국의 지구물리학자인 Harold Jeffreys는 선험적 확률이라는 개념을 전적으로 부정하는 분위기에 맞서 선험확률을 설정할 수 있는 몇 가지 공식을 유도하였는데, 그 중 하나인 Jeffreys’ prior는 현대 베이지안 통계학의 대표적인 무정보적 사전분포로 이용되고 있다.

베이지안 통계학은 제2차대전을 겪으면서 다시 세상에 모습을 드러내었다. 독일의 비밀명령체계인 Enigma를 해독한 영국의 수학자 Alan Turing은 “현재까지 확보된 정보를 이용하여 최상의 추측을 할 필요가 있다. 정보가 추가되는 모든 단계에서 실수의 가능성은 최소화된다.”라고 언급한 바 있으며 암호와 관련된 사전정보를 고려하여 가설에 대한 확률을 추정하는 베이지안 통계학 개념을 이용하였다. 전후 1960년대부터 베이지안 통계학이 본격적으로 활용되기 시작하였다. 베이즈 인자, 칼만필터 등이 이 시기에 고안되었다. 베이즈 인자는 두 모형의 우도함수에 대한 비율이라고 할 수 있으며, 계산 결과를 기반으로 관측된 결과를 더 잘 설명하는 모형이 어느 것인지 판단할 수 있다. 이전 단계의 추정치를 기반으로 관측 정보에 의해 지속적인 예측의 갱신이 이루어지는 칼만필터의 기본적인 개념은 베이지안적 접근을 기반으로 한다.

최근의 베이지안 통계학은 컴퓨터과학의 발전에 따라 인공지능, 기계학습 등과 결합하여 의사결정 문제, 암호화 문제에 적용되는 등 그 활용성이 크게 증대되고 있다. 스팸메일을 필터링하는 나이브 베이즈 분류기법이 하나의 예이다. 메일 제목에 특정한 단어가 있는 경우 그 메일이 스팸메일인지 아닌지를 베이즈 정리를 이용하여 계산함으로써 판단하는 방법이다. 이외에도 수자원 분야에서는 기후변화로 인한 불확실성을 고려하거나 수자원 관리의 의사결정 등에 베이지안 기법이 적용되고 있다. 베이지안 기법과 관련된 다양한 소프트웨어와 라이브러리가 개발되었으며, BUGS (Bayesian inference Using Gibbs Sampling), JAGS (Just Another Gibbs Sampler), STAN (Sampling Through Adaptive Neighborhoods) 등이 대표적이다.

3. 베이즈 정리 및 베이지안 통계학의 특징

3.1 베이즈 정리

베이지안 통계학의 근간이 되는 베이즈 정리는 “확률은 언제든 변할 수 있다.”는 유연한 개념에 근거한다. 확률을 어느 사건이 발생할 가능성에 대한 믿음의 정도로 받아들이는 베이지안 통계학의 고유한 특성이 반영된 개념이다. 어떤 사건 혹은 모수에 대한 최초의 믿음은 베이즈 정리에 의해 객관적인 새로운 정보가 추가됨에 따라 지속적으로 변화한다. 변화 혹은 갱신된 확률은 개선된 믿음의 정도와 같으며, 이러한 일련의 과정은 기본적으로 가변적이라고 가정되는 확률에 대한 참값을 탐색하는 과정과 같다.

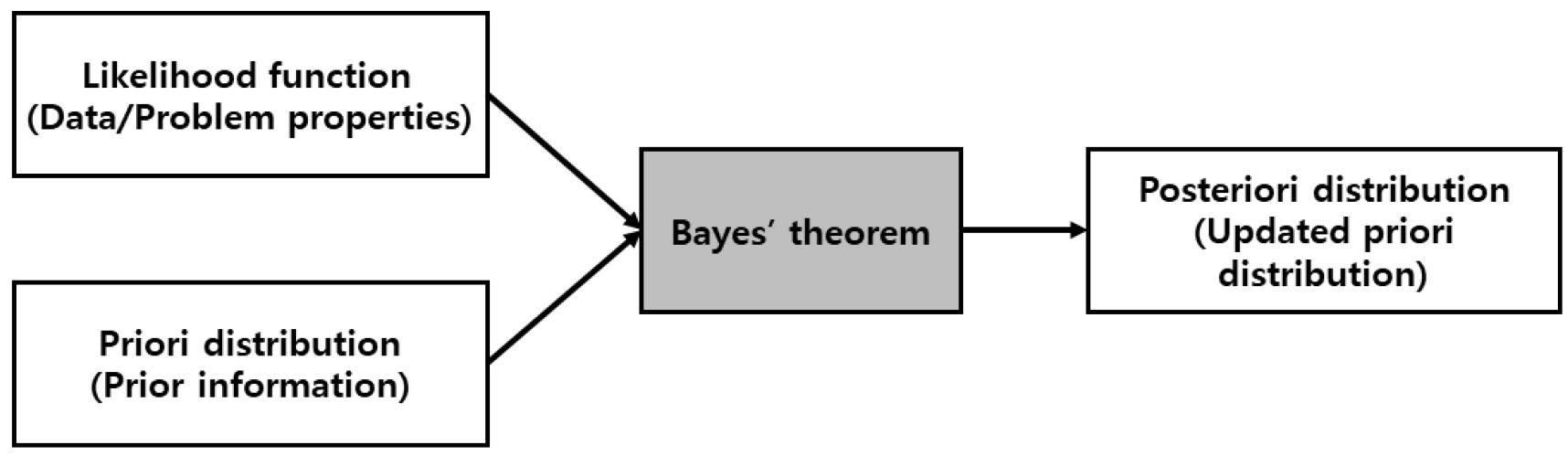
베이즈 정리는 세 가지 요소로 구성된다. 첫 번째 요소는 사전분포(priori distribution)이다. 사전분포는 확률변수에 대한 사전적인 정보를 포함하는 확률분포이다. 두 번째 요소는 우도함수(likelihood function)이다. 우도함수는 사전분포에 적용됨으로써 사전분포의 형태를 변화시키는 역할을 한다. 마지막 요소는 사후분포(posterior distribution)이다. 우도함수가 사전분포에 적용되면서 갱신된 결과가 이에 해당한다. 따라서 사후분포는 사전분포와 우도함수의 곱에 비례한다. 사후분포는 베이즈 정리로 구한 최종적인 결과에 해당하며, 확률변수에 대한 통계적 특성을 제공한다. Fig. 1은 베이즈 정리가 적용되는 흐름인 베이지안 framework를 도시한 것이다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540101/images/kwra_54_01_01_F1.jpg

Fig. 1

Bayesian framework

베이즈 정리의 개념에 비추어 보면 기본적으로 사전분포는 확률변수에 대해 이미 알고 있는 정보 혹은 관련된 선행 정보를 포함하는 형태로 결정되어야 한다. 이를 정보적 사전분포(informative prior distribution)라고 한다. 정보적 사전분포는 추정하고자 하는 확률변수의 과거 관측자료, 유사한 통계적 특성을 보이는 다른 모집단의 자료, 사용자 혹은 전문가의 경험에 기반한 주관적인 판단에 근거하여 결정되는 사전분포를 말한다(Coles and Powell, 1996; Bates and Campbell, 2001). 사전정보를 정량화하기 어렵거나 사전적인 정보가 부족한 경우에는 무정보적(noninformative prior distribution) 사전분포가 이용된다. Uniform 분포, reference prior, Jeffreys’ prior 등 특수한 형태의 확률분포가 이에 해당한다(Gelman et al., 2013). Uniform 분포는 모든 확률변수에 대한 사전확률을 동등하게 부여한 경우이며, reference prior와 Jeffreys’ prior는 발생 가능성이 작은 확률변수의 사전확률을 가중하는 형태이다. 이외에도 계산의 편리함을 위해 beta 분포, gamma 분포, 정규분포와 같은 공액사전분포(conjugated prior distribution)를 이용하는 경우도 있지만, 공액쌍을 만족시키는 경우에만 한정적으로 쓰일 수 있다(Vicens et al., 1975b).

우도함수는 확률변수에 대해 추가로 고려되는 객관적인 자료에 대한 함수를 의미하며, 사후분포를 유도하는 역할을 한다. 우도함수는 해결하고자 하는 문제의 특성을 반영하여 적절한 형태로 결정되어야 한다(Lazar, 2003). 문제의 종류, 유형, 베이지안 기법이 적용되는 목적에 따라 그 형태가 다양하게 결정될 수 있다(Evin et al., 2013). 일례로 Ang and Tang (2007)은 “재료의 결함을 검출하는 시험을 진행함에 따라 재료 결함 크기에 대한 확률분포가 어떻게 바뀔 것인가”라는 문제에 대해 우도함수의 형태를 적절히 결정하였다. 이 문제에서 우도함수는 재료 결함의 크기에 따라 검출되지 않을 가능성을 나타내는 함수로 결정되었다. 즉, 결함의 크기가 클수록 검출이 더 잘될 것이고, 크기가 작을수록 검출이 어려울 것이라는 조정 과정의 특성을 우도함수에 반영한 것이다.

3.2 베이즈 정리의 유도

베이즈 정리는 Bayes와 Laplace의 역확률에 대한 고찰로부터 탄생한 수학 공식이다. 두 사건 A와 B가 서로 종속일 경우, “후행된 B사건에 의해 선행된 A사건의 확률이 어떻게 변화할 것인가”와 같은 문제로부터 유도되었다. 베이즈 정리는 기본적으로 조건부확률의 개념으로부터 출발하는데, 두 사건 A와 B에 대하여 각각의 확률 P(A)와 P(B)가 0이 아니라면 사건 B에 대한 사건 A의 조건부확률 P(A | B)는 다음 식과 같이 정리된다.

(2)

P (A | B) = P (A \cap B) / P (B)

여기서 P(A ∩ B)는 A와 B가 동시에 발생하는 결합확률(joint probability)을 나타내며, P(A | B)는 사건 B가 발생했을 때 사건 A가 발생할 조건부확률(conditional probability)을 나타낸다. Eq. (2)는 사건 B가 선행된 경우에 대한 조건부확률이고, 사건 A가 선행된 경우에 대한 조건부확률은 다음 식과 같이 정리될 수 있다.

(3)

P (B | A) = P (A \cap B) / P (A)

Eqs. (2) and (3)을 P(A ∩ B)에 대해 결합하면 아래의 Eq. (4)가 유도된다.

(4)

P (A | B) P (B) = P (B | A) P (A)

Eq. (4) 좌변의 P(B)를 우변으로 이항시키면 Eq. (5)와 같은 베이즈 정리의 기본 형태를 유도할 수 있다.

(5)

P (A | B) = P (A) P (B | A) / P (B)

베이즈 정리를 이산형 표본공간(discrete sample space)으로 확장하게 되면 ${\{A_{i}\}}_{i = 1}^{n}$ 을 표본공간에 대한 분할이라고 할 때, i에 대하여 Eq. (6)과 같은 일반적인 베이즈 정리의 형태가 유도된다.

(6)

P (A_{i} | B) = \frac{P (B | A_{i}) P (A_{i})}{\sum_{i = 1}^{n} P (B | A_{i}) P (A_{i})}

여기서 P(A_i)는 사전분포, P(B | A_i)는 우도함수, P(A_i | B)는 사후분포를 의미한다. Eq. (6)의 분모는 전확률법칙(law of total probability)에 의해 계산되며, 정규화인자(normalization factor) 혹은 확률변수의 주변분포(marginal distribution)라고 한다. 정규화인자는 사후분포의 확률분포 개념을 만족시키기 위한 역할을 한다. 정규화인자는 계산하기 어려운 경우가 대부분이고, 이를 해결하기 위한 방법으로 공액사전분포(conjugate prior distribution)을 이용하거나 컴퓨터 계산에 기반한 Markov Chain Monte Carlo simulation (MCMC)를 이용한다(Gelman et al., 2013). 공액사전분포는 계산의 편리성을 위해 사전분포와 사후분포의 분포형이 동일하도록 설정한 경우의 사전분포이며, MCMC는 Markov Chain 모형과 Monte Carlo 모의를 결합한 알고리즘으로써 수학적인 유도를 거치지 않더라도 사후분포를 추정할 수 있는 방법이다.

사상(event)에 대한 베이즈 정리는 확률변수 및 분포함수에 대한 베이즈 정리로 확장될 수 있다. 확장된 베이즈 정리는 사전분포와 우도함수를 결합하여 사후분포를 유도하는데 이용된다. 이를 연속형 베이즈 정리라고도 하며, 확률밀도함수로 나타낸 베이즈 정리는 다음 식과 같다.

(7)

π (θ | x_{1}, x_{2}, \dots, x_{n}) = \frac{f (x_{1} | θ) \dots f (x_{n} | θ) π (θ)}{\int_{θ} f (x_{1} | θ) \dots f (x_{n} | θ) π (θ) d θ}

여기서 $θ$ 는 모수이며, $x_{i}$ 는 $θ$ 와 관련된 새로운 정보(자료)이다. $π (θ | x_{1}, x_{2}, \dots, x_{n})$ 은 사후분포, $π (θ)$ 는 $θ$ 의 사전분포이며, Eq. (7) 우변의 분모는 정규화 상수이고, 우변의 분자 중 $f (x_{1} | θ) \dots f (x_{n} | θ)$ 는 발생할 수 있는 모든 가능성을 고려한 우도함수이다.

연속형 베이즈 정리는 이산형 베이즈 정리로 변환될 수 있다. 연속형 베이즈 정리는 확률밀도함수를 대상으로, 이산형 베이즈 정리는 확률질량함수를 대상으로 적용된다. 연속형 확률분포를 이산형으로 변환하는 경우, 확률변수 또한 연속형( $θ$ )에서 이산형( $θ_{i}$ )으로 변환된다. 이때 이산형 모수를 단위구간으로 분할하게 되는데 단위구간의 길이 $∆ θ$ 에 따라 연속형 베이즈 정리와의 차이가 발생하기도 하고 거의 차이가 없을 수도 있다. 즉, $∆ θ$ 가 적정 수준으로 설정되어 연속형 확률과 이산형 확률의 차이가 허용 가능한 범위일 경우에는 변환에 문제가 없을 것으로 판단할 수 있다(Ang and Tang, 2007). 이산형 베이즈 정리는 다음 식과 같다.

(8)

π' (θ_{i}) ∆ θ = \frac{L (θ_{i}) π (θ_{i}) ∆ θ}{\sum_{i = 1}^{n} L (θ_{i}) π (θ_{i}) ∆ θ}

여기서 $π^{'} (θ_{i})$ 는 이산화된 모수 $θ_{i}$ 의 사후확률을 의미하며, $L (θ_{i})$ 와 $π (θ_{i})$ 는 각각 동일한 모수에 대한 우도함수와 사전확률을 의미한다. Eq. (8)의 분모는 연속형과 마찬가지로 정규화인자 즉 상수이고, 따라서 Eq. (8)은 Eq. (9)와 같이 매우 간단한 형태로 정리될 수 있다. Eq. (9)를 통해 사후분포는 사전분포와 우도함수의 곱에 비례함을 알 수 있다.

(9)

π' (θ) = k L (θ) π (θ)

3.3 베이지안 통계학의 특징

베이지안 통계학의 가장 큰 특징은 확률변수에 대한 사전적인 정보를 고려할 수 있다는 점이다(Cornfield, 1967). 사용자의 과거 경험과 주관적 판단, 확률변수와 관련된 추가적인 자료를 통계적 분석에 이용하는 것이 가능하다(Ang and Tang, 2007). Ang and Tang (2007)에서는 콘크리트의 결함 크기에 대한 사전분포를 유도함에 있어 과거의 경험으로부터 얻은 통상적으로 발생하는 결함의 크기에 대한 정보를 이용하였다. 또한, 베이지안 통계학은 최우 원리(principle of likelihood)에 근거한다. 최우 원리란, “세상에 일어나는 일은 일어날 확률이 가장 크기 때문에 일어난 것”이라는 개념이다(Berry, 1987). 최우 원리에 의해 사전확률과 우도확률의 곱, 즉 사후확률은 사건이 발생할 확률이 가장 큰 쪽으로 귀결된다.

둘째로, 추가적인 정보가 부족하거나 주관적인 판단이 어려운 경우에는 사전분포를 임의의 확률분포로 적당히 가정하는 것이 가능하다(Tang et al., 2016). 이를 “불확실성의 법칙(law of insufficiency)” 혹은 “이유 불충분의 원리(principle of indifference)”라고 한다. 베이지안 통계학에서는 이렇게 “확률변수에 대한 어떠한 조건이나 정보가 없으면 우선 가정한다.”, “직감 혹은 상식으로부터 가정한다.”와 같은 접근이 허용된다. 아무런 정보가 없을 경우, 모든 확률변수에 동등한 가능성을 부여하는 균일분포를 이용하기도 한다. 이러한 점들 덕분에 베이지안 통계학은 응용 범위가 상당히 넓다.

베이지안 갱신 개념도 베이지안 통계학의 장점 중 하나이다. Puga et al. (2015)은 베이지안 통계학의 특징을 “Today’s predictions are tomorrow’s priors.”라고 표현하였다. 이는 과거의 결과를 새로운 자료의 분석 대상으로 이용한다는 것, 즉 이전의 자료로부터 산출된 사후확률을 다음 자료 해석을 위한 사전확률로 이용한다는 개념이다. 이를 “축차적 갱신(sequential update)”이라고도 표현하는데, 고려할 수 있는 정보를 축차적으로(차례대로) 이용하는 특성을 말한다. 따라서 베이지안 갱신을 지속적으로 적용하다보면 최신 정보에 의해 결론이 달라질 수 있게 된다. 그렇지만 베이즈 정리는 곱셈법칙에 근거하기 때문에 이전에 사용한 정보는 온전히 사후확률에 반영된다.

4. 수자원 분야의 베이지안 기법 적용 사례

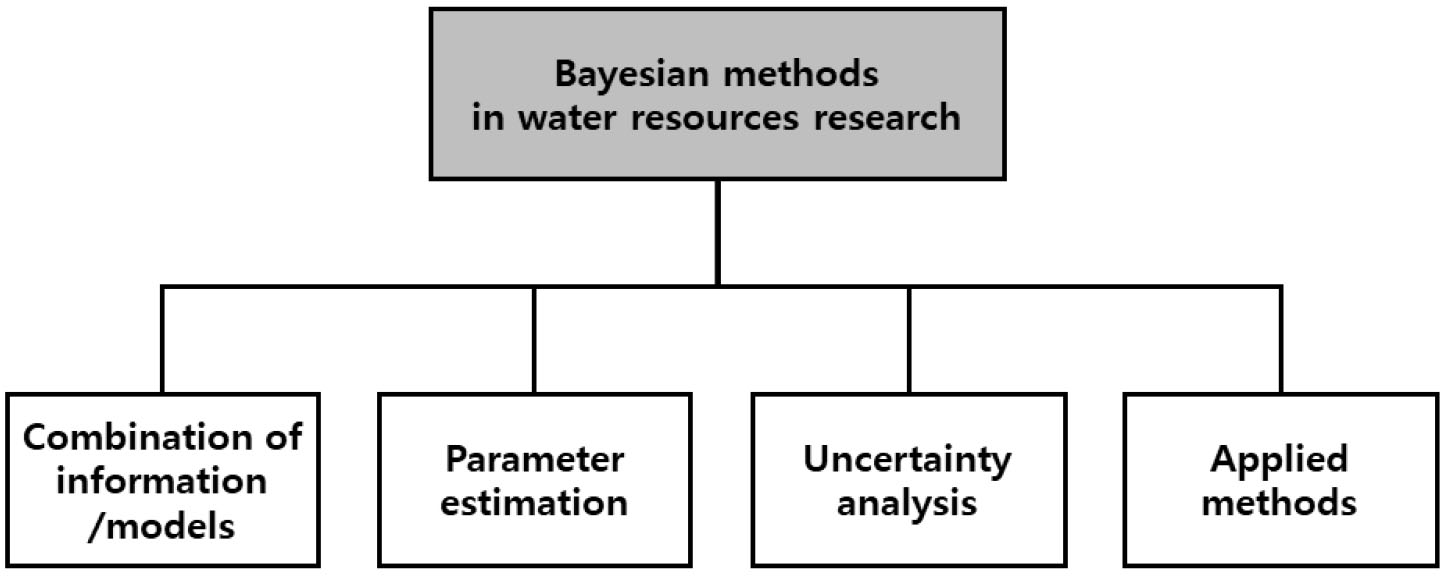
베이지안 기법이 수자원 분야에 적용된 사례는 다양하다(Fig. 2). 정보 혹은 모형을 결합하여 더욱 정확한 확률론적 추론을 한다거나(Raftery et al., 2005; Han and Coulibaly, 2017; Ji et al., 2019), 강우-유출모형 혹은 빈도해석에 이용되는 확률분포의 매개변수 추정에 적용되기도 하고(Ouarda and El-Adlouni, 2011; Viglione et al., 2013; Lima et al., 2018), 예측 및 추정에 대한 불확실성을 정량화하는 용도로 쓰이기도 하였다(Kuczera et al., 2006; Thyer et al., 2009; Tajiki et al., 2020). 또한, 베이지안 기법을 응용한 계층적 베이지안 모형, 베이지안 회귀모형, 베이지안 네트워크 모형, 베이지안 신경망 모형 등이 제시되었다. 이외에도 의사결정, 최적 모형의 선정, 자료의 변동점 탐색, 댐의 최적 운영, 앙상블 유량 예측 등과 같은 문제에 베이지안 기법이 이용되기도 하였다(Kim and Palmer, 1997; Kwon et al., 2008; Stedinger and Kim, 2010; Khan and Coulibaly, 2010; Shenton et al., 2014).

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540101/images/kwra_54_01_01_F2.jpg

Fig. 2

Types of applying the Bayesian method in the water resources field

4.1 정보의 결합

첫 번째 유형은 확률변수와 관련된 여러 정보를 결합하여 자료 분석의 불확실성을 줄이기 위한 목적으로 베이지안 기법을 이용한 사례이다. 대표적으로 Viglione et al. (2013)은 베이지안 기법을 통해 유량 자료를 시공간적으로 확장하여 유량 빈도해석을 수행하였다. Fig. 3과 같은 베이지안 framework를 오스트리아 북부지방의 Kamp river를 대상으로 적용하였다. 시간적 확장에 해당하는 과거 홍수 정보는 우도함수로, 공간적 확장에 해당하는 주위 관측지점들의 정보는 사전분포에 반영하였다. 전문가의 판단도 사전분포의 부분적 정보로 이용하였다. 다음 식은 해당 연구에서 이용한 베이즈 정리이다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540101/images/kwra_54_01_01_F3.jpg

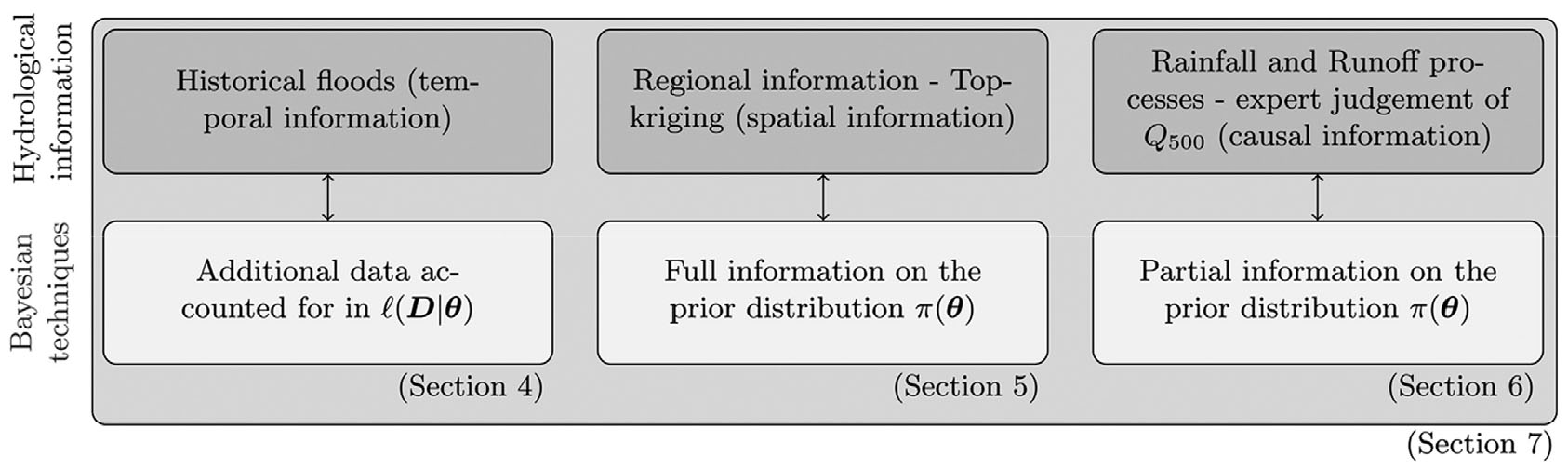
Fig. 3.

Bayesian framework for flood frequency analysis with the spatiotemporal expansion of data (Viglione et al., 2013)

(10)

p (θ | D) \propto [l_{s} (D | θ) l_{H} (D | θ)] [π_{s} (θ) π_{c} (θ)]

여기서 $θ$ 는 유량빈도해석에 이용된 GEV 분포의 매개변수를 의미하며, D는 관측된 유량을 의미한다. 사전분포 $π_{s} (θ) π_{c} (θ)$ 는 40년 이상의 자료를 보유한 주변 관측소들의 연최대유량을 top-kriging하여 얻은 사전정보 $π_{s} (θ)$ 와 재현기간별 확률강우량을 강우-유출해석모형의 입력자료로 이용하여 얻은 재현기간별 유량에 대한 확률분포인 $π_{c} (θ)$ 을 결합한 형태이다. 우도함수 $l_{s} (D | θ) l_{H} (D | θ)$ 은 관측 유량에 대한 우도함수인 $l_{s} (D | θ)$ 와 400년 이전부터 기록된 연최대유량 추정치 중 비정상적으로 큰 값들을 반영한 우도함수인 $l_{H} (D | θ)$ 를 결합한 형태이다.

자료의 시간적 확장에 베이지안 기법을 적용한 사례(Kuczera, 1999; O’Connell et al., 2002; Reis Jr. and Stedinger, 2005)와 분석의 대상이 되는 대상지점 주변 지역의 자료를 추가적인 정보로 이용한 공간적 확장 사례도 있다(Vicens et al., 1975a; Kuczera, 1982; Lee and Kim, 2008; Micevski and Kuczera, 2009). 이외에도 정보를 결합하는 다양한 형태의 연구가 수행되었다. Seo and Smith (1991)는 정확도가 낮은 레이더 강우자료와 공간밀도가 성근 우량계 관측치의 단점을 보완하고자 새로운 자료가 들어올 때마다 매개변수가 갱신되는 강우추정식을 이용하여 미계측 지점의 강우량을 추정하였다. Coles and Tawn (1996)은 극치강우자료의 확충을 위해 전문가의 지식에 기반한 분위 추정치를 사전분포에 반영하여 빈도해석을 수행하였다. Kim and Palmer (1997)은 저수지의 최적 운영에 계절 및 월별 유량 예측정보를 추가적인 정보로 이용하는 Bayesian Stochastic Dynamic Programming (BSDP)를 적용하였다.

4.2 모형의 결합: 앙상블 개념

베이지안 기법은 여러 모형을 결합하는 앙상블 개념으로 이용되기도 한다. 여러 모형의 모의치 혹은 예측치를 베이지안 기법을 통해 결합하여 예측 품질을 향상시키는 방법이다. 베이지안 앙상블 개념은 Krzysztofowicz (1999)에 의해 처음 제시되었으며, 주로 기상인자, 유량, 수위의 예측에 적용되었다(Raftery et al., 2005; Duan et al., 2007). 베이지안 앙상블 예측은 최적의 예측치를 제공함과 동시에 앙상블 예측치에 대한 사후분포로부터 예측의 불확실성 평가를 가능케 한다(Han and Coulibaly, 2017). 또한, 각각의 모형에 대한 불확실성도 확인할 수 있어 모형간의 비교도 가능하다(Duan et al., 2007). 베이지안 앙상블 예측 개념은 수위와 유량의 예측에도 적용되었다(Krysztofowicz, 1999; Maranzano and Krzysztofowicz, 2004).

베이지안 앙상블 기법의 적용 사례로는 Raftery et al. (2005)이 대표적이다. Raftery et al. (2005)은 Bayesian Model Averaging (BMA) 기법을 이용하여 미국의 Pacific Northwest 지역을 대상으로 5개 모형의 해수면 온도 예측치를 결합하였다. BMA는 여러 모형에서 생성된 각각의 예측치에 가중치를 부여하여 앙상블 가중평균치를 제공하는 방법인데, 가중치는 각 앙상블 멤버로부터 기대되는 예측의 정도인 사후확률을 통해 결정된다(Eq. (11)). 좋은 예측성능을 보이는 예측치일수록 더 큰 값이 부여되고, 그렇지 않은 예측치에는 작은 값이 부여된다(Hoeting et al., 1999).

(11)

p (y) = \sum_{k = 1}^{K} p (y | M_{k}) p (M_{k} | y^{T})

여기서 $p (y | M_{k})$ 는 모형 M_k에 대한 확률변수 y의 분포를 의미하며, Fig. 4에서 여러 얇은 선 그래프들은 각 모형의 $p (y | M_{k})$ 을 의미한다. $p (M_{k} | y^{T})$ 는 학습자료 y^T에 모형 M_k가 어느 정도 적합한지를 나타내는 사후분포이며, 각 모형의 가중치 역할을 한다. 사후확률 $p (M_{k} | y^{T})$ 을 계산하는 과정에는 베이즈 정리 기반의 최대가능도 탐색 기법인 EM (Expectation-Maximization) 알고리즘이 이용된다. $p (y)$ 는 베이지안 앙상블 가중평균 확률분포를 의미하며, Fig. 4의 굵은 실선이다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540101/images/kwra_54_01_01_F4.jpg

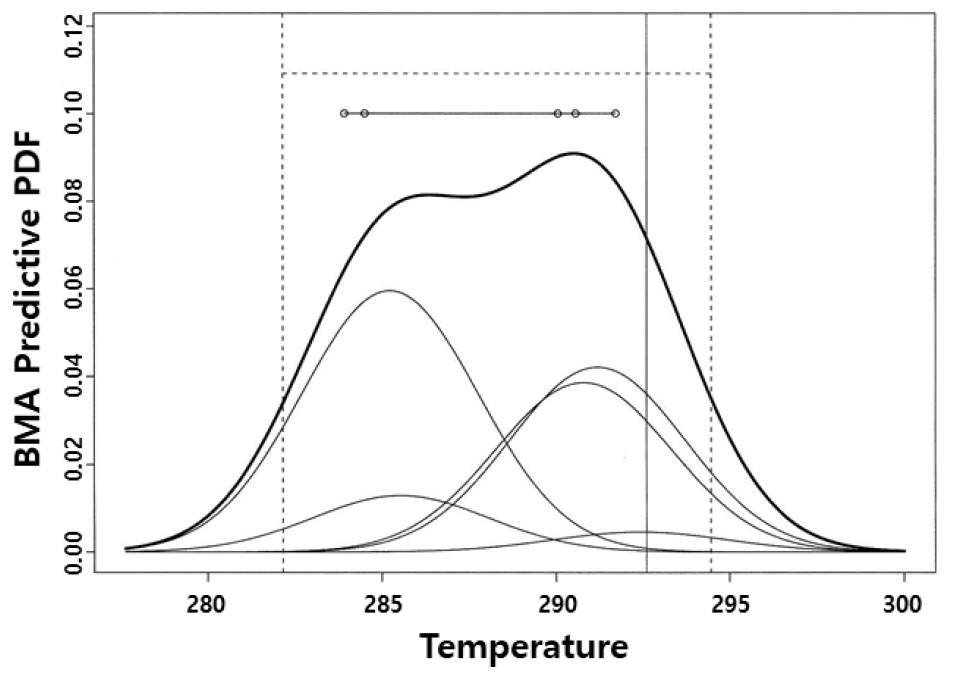
Fig. 4

Derivation of the posteriori distribution with the BMA for weather forecasting (Raftery et al., 2005)

4.3 통계적 추론: 매개변수 추정

베이지안 기법은 매개변수 추정시 최적화 기법이 가지는 한계를 극복할 수 있는 하나의 대안이 될 수 있다. 기존의 최적화 기법은 과적합(overfitting) 문제와 함께 매개변수 추정에 대한 정확도를 정량화할 수 없다는 한계를 가진다(Yang et al., 2007). 이러한 문제는 베이지안 기법 적용 결과인 사후분포를 통해 해결될 수 있다. 사후분포의 대푯값으로부터 매개변수 추정치를 결정할 수 있고, 불확실성은 사후분포의 분산으로 정량화된다. 더 나아가 매개변수 추정 범위를 사전분포에 반영할 수 있기 때문에 타당한 추정이 가능하다.

베이지안 MCMC는 매개변수 추정시 사후분포의 유도에 이용되는 계산 기법이다(Smith and Marshall, 2008). MCMC는 Markov Chain 모형과 Monte Carlo 모의를 결합한 알고리즘이다. Markov Chain은 현재 시점의 추정이 바로 이전 시점의 추정치에만 영향을 받는 시계열 모형이며, Monte Carlo 모의는 무작위 추출 기법으로써 갱신된 현재 시점의 사후분포로부터 확률변수를 임의 추출하는 과정을 반복함으로써 매개변수의 사후분포를 유도하는 데 이용된다. MCMC의 계산 알고리즘으로는 Metropolis-Hastings Sampling, Gibbs Sampling이 가장 많이 쓰이고 있다(Kavetski et al., 2006).

베이지안 기법을 이용한 매개변수 추정은 주로 강우-유출해석에 이용되는 수문모형과 빈도해석에 이용되는 확률분포에 적용되었다(Thiemann et al., 2001; Ouarda and El-Adlouni, 2011; Wellen et al., 2014). 기본적으로 베이지안 기법을 이용한 매개변수 추정 과정은 매개변수의 특성을 고려한 사전분포의 결정, 관측치에 근거한 우도함수의 결정, MCMC를 이용한 사후분포 유도 및 매개변수 추정치 결정 순으로 진행된다. Engeland and Gottschalk (2002)는 NOrthern hemisphere climate-Processes land-surface EXperiment (NOPEX) 지역 내 미계측 유역을 대상으로 유량을 모의하는 ECOlogical Model for Applied Geophysics (ECOMAG) 모형의 매개변수 추정에 베이지안 기법을 적용하였다. 사전분포는 9개의 매개변수 각각에 대해 적절한 범위의 균일분포로 결정하였으며, 우도함수로는 관측치와 모의치의 차이, 분산의 비율 등을 고려한 세 가지 형태를 이용하였다. 다음 식은 해당 연구에서 이용한 베이즈 정리이다.

(12)

P (θ | Y) = \frac{L (Y | θ) P (θ)}{C}

여기서 $θ$ 는 ECOMAG 모형의 매개변수이며, C는 정규화 상수이다. $P (θ)$ 는 사전분포, $L (Y | θ)$ 는 모형의 매개변수 $θ$ 와 관측치 Y의 관계를 나타내는 우도함수이다. 사후분포 $P (θ | Y)$ 는 MCMC를 거쳐 유도된다.

빈도해석에 이용되는 확률분포의 매개변수 추정도 유사한 과정을 거치게 된다. Lee and Kim (2008)는 저유량의 빈도해석에 이용되는 2모수 Weibull 분포의 매개변수를 베이지안 기법을 통해 추정하였다. 사전분포로는 임의의 형태로 결정한 무정보적 사전분포와 관측지점 주변의 자료들을 이용한 정보적 사전분포 두 가지를 이용하였다. 다음 Eq. (13)은 해당 연구에서 이용한 베이즈 정리이며, Eq. (14)는 우도함수이다.

(13)

π (α, β | D) = \frac{L (D | α, β) π (α, β)}{\int_{0}^{\infty} \int_{0}^{\infty} L (D | α, β) π (α, β) d α d β}

(14)

L (D | α, β) = {(\frac{α}{β})}^{n} \prod_{i = 1}^{n} {(\frac{x_{i}}{β})}^{α - 1} \exp [- \sum_{i = 1}^{n} {(\frac{x_{i}}{β})}^{α}]

여기서 $α$ 는 형상매개변수, $β$ 는 규모매개변수이며, D는 관측된 저유량 x_i의 집합을 의미한다. 사전분포인 $π (α, β)$ 는 두 매개변수가 서로 독립이라면 $π (α, β) = π (α) π (β)$ 을 만족하게 되고, $π (α)$ 와 $π (β)$ 는 각각 결정된다. 우도함수 $L (D | α, β)$ 는 매개변수가 $α$ 와 $β$ 인 경우에 유도되는 Weibull 분포의 관측유량 x_i에 대한 확률을 모두 곱하는 형태이다(Eq. (14)). 이러한 형태의 우도함수는 확률분포의 매개변수 추정을 시도한 유사한 연구들에서 찾아볼 수 있다(Reis Jr. and Stedinger, 2005; Kaheil et al., 2006).

4.4 불확실성 정량화

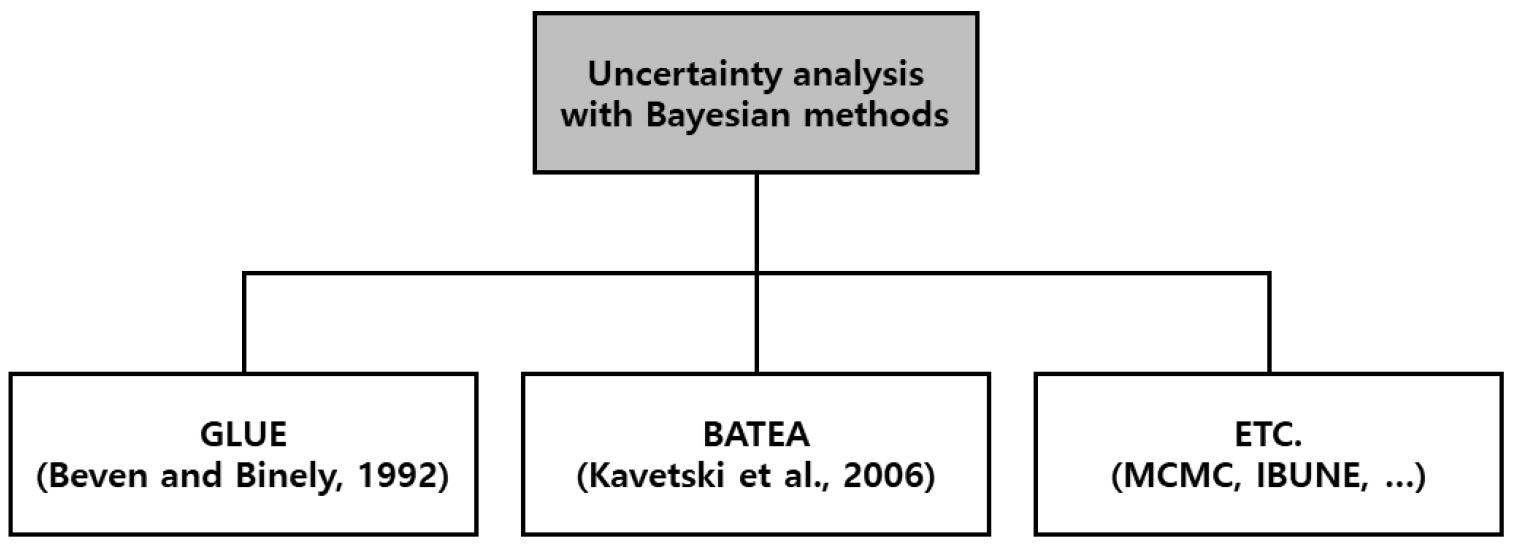
베이지안 통계학에서는 모형의 매개변수 추정 결과는 항상 불확실성을 포함하고 있으며, 불확실성은 사후분포의 분산으로 정량화된다고 본다(Krzysztofowicz, 1999). 베이지안 갱신 개념을 이용하는 Generalized Likelihood Uncertainty Estimation (GLUE), 수문모형을 구성하는 인자들에 대한 불확실성을 확인할 수 있는 BAyesain Total Error Analysis (BATEA), BATEA와 BMA를 결합한 Integrated Bayesian Uncertainty Estimator (IBUNE) 등 여러 방법이 활용된 바 있다(Beven and Binely, 1992; Kuczera et al., 2006; Ajami et al., 2007). Fig. 5는 불확실성 분석에 적용된 베이지안 기법들이다.

GLUE는 Beven and Binely (1992)가 제시한 베이지안 갱신 기반의 불확실성 정량화 방법이다. GLUE는 모형의 구조 및 매개변수는 자료 혹은 정보가 추가됨에 따라 달라질 수 있다는 개념을 기반으로 한다. 추가되는 자료의 특성을 반영한 우도함수를 연속적으로 적용하고, 그 결과인 사후분포를 통해 모의에 대한 불확실성을 평가하는 방법이다(Kuczera and Parent, 1998; Vrugt et al., 2009). Freer et al. (1996)은 독일 Ringelbach 유역의 유량 모의에 대한 불확실성 변화를 분석하는 데 GLUE를 적용하였다. 매년별 자료를 우도함수로 이용하여 사후분포를 갱신하였다. Eq. (15)는 GLUE의 근간이 되는 베이즈 정리이다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540101/images/kwra_54_01_01_F5.jpg

Fig. 5

Bayesian methods used for uncertainty analysis

(15)

L (θ_{i} | Y) = L (Y | θ_{i}) L_{0} (θ_{i}) / C

여기서 $L_{0} (θ_{i})$ 는 매개변수에 대한 사전분포로써 이전 연도의 사후분포인 $L (θ_{i - 1} | Y)$ 와 같다. $L (Y | θ_{i})$ 는 매개변수 $θ_{i}$ 인 모형의 모의치와 관측치 Y의 관계를 나타내는 우도함수이며, 우도함수가 사전분포에 반영됨으로써 사후분포 $L (θ_{i} | Y)$ 가 유도된다.

BATEA는 Kavetski et al. (2006)에 의해 제시된 입력, 시스템, 출력을 고려한 모형의 불확실성 정량화 방법이다. 샘플링 혹은 관측오차에 의해 수문모형의 입력(주로 강수자료)과 출력(주로 유량자료)이 모두 불확실성을 가질 수 있다는 개념을 기반으로 한다(Kuczera et al., 2006; Thyer et al., 2009). 사전분포는 입력과 출력의 불확실성에 관한 것이며, 우도함수는 관측치를 기반으로 결정된다. 사후분포가 갱신되면서 입력과 출력의 불확실성이 정량화된다. Eq. (16)은 BATEA에서 이용되는 베이즈 정리를 나타낸 것이고, Eq. (17)은 사전분포이다.

(16)

p (θ, ϕ, β_{x}, β_{y} | \tilde{X}, \tilde{Y}) = \frac{p (\tilde{Y} | θ, \tilde{X}, ϕ, β_{x}, β_{y}) p (θ, ϕ, β_{x}, β_{y})}{p (\tilde{Y} | \tilde{X})}

(17)

p (θ, ϕ, β_{x}, β_{y}) = p (θ) p (ϕ | β_{x}) p (β_{x}) p (β_{y})

여기서 $\tilde{X}$ 와 $\tilde{Y}$ 는 각각 불확실성을 포함하는 입력자료와 출력자료이고, $ϕ$ 는 무작위 변수로써 입력자료에 더해짐으로써 고려된다. $θ$ 는 모형의 매개변수, $β_{x}$ 와 $β_{y}$ 는 각각 입력과 출력에 대한 오차모형의 매개변수이다. 우도함수 $p (\tilde{Y} | θ, \tilde{X}, ϕ, β_{x}, β_{y})$ 는 여러 매개변수들과 입력자료가 결정된 경우의 출력값에 대한 함수이다. 사전분포 $p (θ, ϕ, β_{x}, β_{y})$ 는 각 매개변수에 대한 사전분포의 결합으로 이루어진다. 사후분포 $p (θ, ϕ, β_{x}, β_{y} | \tilde{X}, \tilde{Y})$ 를 통해 각 매개변수의 불확실성이 정량화된다.

4.5 응용기법 및 기타 적용 사례

베이지안 기법을 응용한 다양한 기법들이 있다. 그 중 하나가 계층적 베이지안 모형(Hierarchical Bayeisan Model, HBM)이다. 계층적 베이지안 모형은 주어진 문제를 여러 계층으로 나누어 베이지안 기법을 적용하는 방법으로 수문모형 및 확률분포의 매개변수를 추정하는데 이용된 바 있다(Marshall et al., 2007; Najafi and Moradkhani, 2014). 확률분포의 매개변수 추정을 예로 들면, 기본적인 베이지안 추론에서는 매개변수의 사전분포를 균일분포나 비모수 모형으로 가정하는 반면 계층적 베이지안 모형에서는 매개변수의 사전분포를 초모수(hyper-parameter)를 가지는 또다른 확률분포로 설정한다. 즉, 사전분포에 대한 상위의 사전분포가 있는 형태이다. Kwon et al. (2008)은 Montana 지역의 유량자료를 대상으로 시간의 흐름에 따라 확률분포의 매개변수가 변화하는 비정상 빈도해석을 수행하는데 계층적 베이지안 모형을 이용하였다. 연최대치유량 자료에 적합한 Gumbel 분포의 매개변수는 기후인자들을 독립변수로하는 회귀식에서의 종속변수로 설정하였다. 이때 회귀식의 계수들은 각각 또다른 초모수를 가지는 정규분포를 따르고, 베이지안 MCMC를 이용하여 Gumbel 분포의 매개변수를 최종적으로 추정하였다. 다음 식은 해당 연구에서 적용한 계층모형을 나타낸 것이다.

(18)

Z (t) ~ G u m b e l (μ (t), σ) μ (t) = β_{0} + β_{1} X_{1} (t) + \dots + β_{k} X_{k} (t) β_{i} ~ N (η_{i}, σ_{i}) p (η_{i}) = N (0, σ_{σ_{i}}) p (σ_{i}) = \frac{1}{π γ [1 + {(\frac{σ_{i}}{γ})}^{2}]}

여기서 $μ (t)$ 가 최종적으로 결정되어야 하는 Gumbel 분포의 매개변수이고, X_i는 고려된 기후인자들이다. $μ (t)$ 는 X_i에 대한 회귀식으로 결정되고, 회귀식의 계수 $β_{i}$ 는 초모수 $η_{i}$ 와 $σ_{i}$ 에 의해 결정된 정규분포를 따른다. 그리고 두 초모수에 대한 사전분포는 각각 정규분포와 half-Cauchy distribution으로 가정하였다. MCMC를 통해 유도되는 사후분포는 곧 $μ (t)$ 에 대한 확률분포를 의미한다.

또 다른 응용기법으로 베이지안 네트워크 모형(Bayesian Network Model, BNM)이 있다. 베이지안 네트워크는 여러 변수들간의 다양한 종속관계를 보여주는 비순환적 관계도이다(Chan et al., 2012; Shenton et al., 2014). 변수들을 node로, 변수들간의 관계를 link로 표시하며, node간의 연관성을 정량화하는데 원인과 결과의 조건부확률을 기반으로 한 베이즈 정리를 이용한다. 지하수량, 유사량, 지형학적 변화의 평가에도 적용되었으며(Mount and Stott, 2008; Fienen et al., 2013; Liedloff et al., 2013), 가뭄예측(Shin et al., 2016; Madadgar and Moradkhani, 2013), 상수도 관망의 운영(Dawsey et al., 2007; Perelman and Ostfeld, 2010) 등에도 적용되었다. Smith (2006)에서는 결과(effect)를 유발한 원인(cause)들의 영향을 정량화하는데 Eq. (19)와 같은 베이즈 정리를 이용하였다. 네트워크를 구성하는 모든 link에 대해 사후확률이 다음 식을 통해 계산된다.

(19)

P (c a u s e | e f f e c t) = \frac{P (c a u s e) P (e f f e c t | c a u s e)}{P (e f f e c t)}

최근에는 기계학습과 베이지안 기법을 결합한 베이지안 신경망(Bayesian Neural Network, BNN) 모형이 등장하였다. BNN은 기존의 ANN 모형과 동일한 framework이며, 학습 과정도 유사하다. 다만, BNN에서는 학습을 통해 layer간의 관계를 나타내는 신경망 매개변수(연결가중치, 편의)를 결정하는 데에 베이지안 기법을 이용한다(Khan and Koulibaly, 2010). 확정적인 하나의 매개변수를 제공하는 것이 아니라 매개변수의 사후분포로부터 확률론적 추정치와 그에 대한 불확실성을 제공하는 것이다(Zhang et al., 2011; Zhang and Zhao, 2012). 사전분포는 학습 이전의 신경망 매개변수에 대한 사전정보를 통해 결정되며, 우도함수는 자료와 목적함수를 기반으로 결정된다. Khan and Koulibaly (2010)는 BNN을 유출량의 모의에 적용하였다. 캐나다의 Saguenay-Lac-Saint-Jean 유역에 적용한 결과, ANN, 강우-유출모형(HBV-96 모형)보다 BNN이 더 적절한 모의치를 제공하였음을 확인하였다. Eq. (20)은 BNN의 근간이 되는 베이즈 정리를 나타낸 것이다.

(20)

p (w | D) = \frac{p (D | w) p (w)}{p (D)}

여기서 $w$ 는 가중치를 의미하며 D는 관측치이다. 가중치에 대한 사전분포 $p (w)$ 는 임의로 가정되며, 자료가 추가되면서 사후분포 $p (w | D)$ 로 갱신된다.

5. 결 론

본 연구에서는 베이지안 기법의 발전 과정 및 수자원 분야에 적용된 사례를 소개하였다. 먼저, 베이지안 통계학의 탄생에서부터 현재에 이르기까지의 발전 과정과 이에 기여한 베이지안 통계학자들의 업적 등을 정리하였다. 다음으로 베이지안 기법의 근간이 되는 베이즈 정리를 유도하고, 베이즈 정리의 세 요소인 사전분포, 우도함수, 사후분포의 역할에 대해 설명하였다. 또한, 베이지안 통계학이 가지는 고유한 특징과 장점에 대해 정리하였다. 마지막으로 수자원 분야에 베이지안 기법이 적용된 사례를 여러 범주로 나누어 정리하였다.

베이지안 통계학은 이제 더이상 특이하거나 생소한 개념이 아니다. 오히려 수자원 분야 연구에서 유용한 도구의 역할을 하고 있다. 선험적 정보와 주관성을 사전적 정보로 이용하고, 관측자료 기반의 축차적인 갱신을 토대로 하는 베이지안 통계학 특유의 추론 방식에 대한 효용성은 이미 많은 연구 사례들을 통해 증명되었다. 수문학적 모형의 매개변수 추정과 동시에 불확실성을 제공할 수도 있으며, 수문학적 인과관계에 대한 분석 및 의사결정의 도구로도 활용될 수 있다. 정보화 및 빅데이터의 활용이 더욱 활발해질 가까운 미래에는 베이지안 통계학의 활용도가 더욱 높아질 것으로 전망된다. 수자원 분야에서도 이러한 변화가 도래하게 될 가능성이 매우 크기 때문에 앞으로 베이지안 통계학의 적극적인 활용이 기대되는 바이다.

Acknowledgements

이 성과는 2020 년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2020R1A2C200871411).

References

Ait-El-Fquih, B., Gharamti, M.E., and Hoteit, I. (2016). "A Bayesian consistent dual ensemble Kalman filter for state-parameter estimation in subsurface hydrology." Hydrology and Earth System Sciences, Copernicus, Vol. 20, No. 8, pp. 3289-3307. 10.5194/hess-20-3289-2016

Ajami, N.K., Duan, Q., and Sorooshian, S. (2007). "An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction." Water Resources Research, Wiley, Vol. 43, No. 1, W01403. 10.1029/2005WR004745

Ang, A.H.S., and Tang, W.H. (2007). Probability concepts in engineering planning and design: Emphasis on application to civil and environmental engineering. Wiley, New York, N.Y.

Bates, B.C., and Campbell, E. (2001). "A markov chain monte carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling." Water Resources Research, Wiley, Vol. 37, No. 4, pp. 937-947. 10.1029/2000WR900363

Berger, J.O. (2000). "Bayesian analysis: A look at today and thoughts of tomorrow." Journal of the American Statistical Association, Taylor & Francis, Vol. 95, No. 452, pp. 1269-1276. 10.1080/01621459.2000.10474328

Berry, D.A. (1987). "Interim analysis in clinical trials: The role of the likelihood principle." The American Statistician, Taylor & Francis, Vol. 41, No. 2, pp. 117-122. 10.1080/00031305.1987.10475458

Beven, K., and Binley, A. (1992). "The future of distributed models: Model calibration and uncertainty prediction." Hydrological Processes, Wiley, Vol. 6, No. 3, pp. 279-298. 10.1002/hyp.3360060305

Chan, T.U., Hart, B.T., Kennard, M.J., Pusey, B.J., Shenton, W., Douglas, M.M., Valentine, E., and Patel, S. (2012). "Bayesian network models for environmental flow decision making in the Daly River, Northern Territory, Australia." River Research and Applications, Wiley, Vol. 28, No. 3, pp. 283-301. 10.1002/rra.1456

Coles, S.G., and Powell, E.A. (1996). "Bayesian methods in extreme value modelling: A review and new developments." International Statistical Review, Wiley, Vol. 64, No. 1, pp. 119-136. 10.2307/1403426

Coles, S.G., and Tawn, J.A. (1996). "A Bayesian analysis of extreme rainfall data." Journal of the Royal Statistical Society, Wiley, Vol. 45, No. 4, pp. 463-478. 10.2307/2986068

Cornfield, J. (1967). "Bayes theorem." Review of the International Statistical Institute, Vol. 35, No. 1, pp. 34-49. 10.2307/1401634

Dawsey, W.J., Minsker, B.S., and Amir, E. (2007). "Real time assessment of drinking water systems using a dynamic Bayesian network." Proceedings World Environmental and Water Resources Congress 2007: Restoring Our Natural Habitat, ASCE, Tampa, FL, pp. 1-6. 10.1061/40927(243)507

Di, S., Kondo, D., and Cirne, W. (2014). "Google hostload prediction based on Bayesian model with optimized feature combination." Journal of Parallel and Distributed Computing, Elsevier, Vol. 74, No. 1, pp. 1820-1832. 10.1016/j.jpdc.2013.10.001

Duan, Q., Ajami, N.K., Gao, X., and Sorooshian, S. (2007). "Multi-model ensemble hydrologic prediction using Bayesian model averaging." Advances in Water Resources, Elsevier, Vol. 30, No. 5, pp. 1371-1386. 10.1016/j.advwatres.2006.11.014

Engeland, K., and Gottschalk, L. (2002). "Bayesian estimation of parameters in a regional hydrological model." Hydrology and Earth System Sciences, Copernicus, Vol. 6, No. 5, pp. 883-898. 10.5194/hess-6-883-2002

Evin, G., Kavetski, D., Thyer, M., and Kuczera, G. (2013). "Pitfalls and improvements in the joint inference of heteroscedasticity and autocorrelation in hydrological model calibration." Water Resources Research, Wiley, Vol. 49, No. 7, pp. 4518-4524. 10.1002/wrcr.20284

Fienberg, S.E. (2006). "When did Bayesian inference become "Bayesian"?" Bayesian Analysis, ISBA, Vol. 1, No. 1, pp. 1-40. 10.1214/06-BA101

Fienen, M.N., Masterson, J.P., Plant, N.G., Gutierrez, B.T., and Thieler, E.R. (2013). "Bridging groundwater models and decision support with a Bayesian network." Water Resources Research, Wiley, Vol. 49, No. 10, pp. 6459-6473. 10.1002/wrcr.20496

Freer, J., Beven, K., and Ambroise, B. (1996). "Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach." Water Resources Research, Wiley, Vol. 32, No. 7, pp. 2161-2173. 10.1029/95WR03723

Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A., and Rubin, D.B. (2013). Bayesian data analysis. CRC press, Boca Raton, F.L., U.S. 10.1201/b16018

Han, S., and Coulibaly, P. (2017). "Bayesian flood forecasting methods: A review." Journal of Hydrology, Elsevier, Vol. 551, pp. 340-351. 10.1016/j.jhydrol.2017.06.004

Hoeting, J.A., Madigan, D., Raftery, A.E., and Volinsky, C.T. (1999). "Bayesian model averaging: A tutorial." Statistical Science, IMS, Vol. 14, No. 4, pp. 382-401. 10.1214/ss/1009212519

Insua, D.R., Diez, R.M., and Palomo, J. (2002) "Bayesian methods in Hydrology: A review." Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas, Springer, Vol. 96, No. 3, pp. 461-479.

Ji, L., Zhi, X., Zhu, S., and Fraedrich, K. (2019). "Probabilistic precipitation forecasting over East Asia using Bayesian model averaging." Weather and Forecasting, AMS, Vol. 34, No. 2, pp. 377-392. 10.1175/WAF-D-18-0093.1

Kaheil, Y.H., Gill, M.K., McKee, M., and Bastidas, L. (2006). "A new Bayesian recursive technique for parameter estimation." Water Resources Research, Wiley, Vol. 42, No. 8, W08423. 10.1029/2005WR004529

Kavetski, D., Kuczera, G., and Franks, S.W. (2006). "Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory." Water Resources Research, Wiley, Vol. 42, No. 3, W03407. 10.1029/2005WR004368

Khan, M.S., and Coulibaly, P. (2010). "Assessing hydrologic impact of climate change with uncertainty estimates: Bayesian neural network approach." Journal of Hydrometeorology, AMS, Vol. 11, No. 2, pp. 482-495. 10.1175/2009JHM1160.1

Kim, Y.O., and Palmer, R.N. (1997). "Value of seasonal flow forecasts in Bayesian stochastic programming." Journal of Water Resources Planning and Management, ASCE, Vol. 123, No. 6, p. 335. 10.1061/(ASCE)0733-9496(1997)123:6(327)

Krzysztofowicz, R. (1999). "Bayesian theory of probabilistic forecasting via deterministic hydrologic model." Water Resources Research, Wiley, Vol. 35, No. 9, pp. 2739-2750. 10.1029/1999WR900099

Kuczera, G. (1982). "Combining site-specific and regional information: An empirical Bayes approach." Water Resources Research, Wiley, Vol. 18, No. 2, pp. 306-314. 10.1029/WR018i002p00306

Kuczera, G. (1999). "Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference." Water Resources Research, Wiley, Vol. 35, No. 5, pp. 1551-1557. 10.1029/1999WR900012

Kuczera, G., Kavetski, D., Franks, S., and Thyer, M. (2006). "Towards a Bayesian total error analysis of conceptual rainfall-runoff models: Characterising model error using storm-dependent parameters." Journal of Hydrology, Elsevier, Vol. 331, No. 1-2, pp. 161-177. 10.1016/j.jhydrol.2006.05.010

Kuczera, G., and Parent, E. (1998). "Monte Carlo assessment of parameter uncertainty in conceptual catchment models: the Metropolis algorithm." Journal of Hydrology, Elsevier, Vol. 211, No. 1-4, pp. 69-85. 10.1016/S0022-1694(98)00198-X

Kwon, H.H., Brown, C., and Lall, U. (2008). "Climate informed flood frequency analysis and prediction in Montana using hierarchical Bayesian modeling." Geophysical Research Letters, Wiley, Vol. 35, No. 5, L05404. 10.1029/2007GL032220

Lazar, N.A. (2003). "Bayesian empirical likelihood." Biometrika, Oxford Academic, Vol. 90, No. 2, pp. 319-326. 10.1093/biomet/90.2.319

Lee, J., Lee, K., and Lee, Y. (2014). "History and future of Bayesian statistics." The Korean Journal of Applied Statistics, KJAS, Vol. 27, No. 6, pp. 855-863. 10.5351/KJAS.2014.27.6.855

Lee, K.S., and Kim, S.U. (2008). "Identification of uncertainty in low flow frequency analysis using Bayesian MCMC method." Hydrological Processes: An International Journal, Wiley, Vol. 22, No. 12, pp. 1949-1964. 10.1002/hyp.6778

Liedloff, A.C., Woodward, E.L., Harrington, G.A., and Jackson, S. (2013). "Integrating indigenous ecological and scientific hydro-geological knowledge using a Bayesian network in the context of water resource development." Journal of Hydrology, Elsevier, Vol. 499, pp. 177-187. 10.1016/j.jhydrol.2013.06.051

Lima, C.H., Kwon, H.H., and Kim, Y.T. (2018). "A local-regional scaling-invariant Bayesian GEV model for estimating rainfall IDF curves in a future climate." Journal of Hydrology, Elsevier, Vol. 566, pp. 73-88. 10.1016/j.jhydrol.2018.08.075

Madadgar, S., and Moradkhani, H. (2013). "A Bayesian framework for probabilistic seasonal drought forecasting." Journal of Hydrometeorology, AMS, Vol. 14, No. 6, pp. 1685-1705. 10.1175/JHM-D-13-010.1

Maranzano, C.J., and Krzysztofowicz, R. (2004). "Identification of likelihood and prior dependence structures for hydrologic uncertainty processor." Journal of Hydrology, Elsevier, Vol. 290, No. 1-2, pp. 1-21. 10.1016/j.jhydrol.2003.11.021

Marshall, L., Nott, D., and Sharma, A. (2007). "Towards dynamic catchment modelling: A Bayesian hierarchical mixtures of experts framework." Hydrological Processes: An International Journal, Wiley, Vol. 21, No. 7, pp. 847-861. 10.1002/hyp.6294

McGrayne, S.B. (2011). The theory that would not die: how Bayes' rule cracked the enigma code, hunted down Russian submarines, & emerged triumphant from two centuries of controversy. Yale University Press, New Haven, C.T. U.S.

Micevski, T., and Kuczera, G. (2009). "Combining site and regional flood information using a Bayesian Monte Carlo approach." Water Resources Research, Wiley, Vol. 45, No. 4, W04405. 10.1029/2008WR007173

Mount, N., and Stott, T. (2008). "A discrete Bayesian network to investigate suspended sediment concentrations in an Alpine proglacial zone." Hydrological Processes: An International Journal, Wiley, Vol. 22, No. 18, pp. 3772-3784. 10.1002/hyp.6981

Najafi, M.R., and Moradkhani, H. (2014). "A hierarchical Bayesian approach for the analysis of climate change impact on runoff extremes." Hydrological Processes, Wiley, Vol. 28, No. 26, pp. 6292-6308. 10.1002/hyp.10113

O'Connell, D.R., Ostenaa, D.A., Levish, D.R., and Klinger, R.E. (2002). "Bayesian flood frequency analysis with paleohydrologic bound data." Water Resources Research, Wiley, Vol. 38, No. 5, pp. 16-1-16-13. 10.1029/2000WR000028

Ouarda, T.B.M.J., and El‐Adlouni, S. (2011). "Bayesian nonstationary frequency analysis of hydrological variables." Journal of the American Water Resources Association, Wiley, Vol. 47, No. 3, pp. 496-505. 10.1111/j.1752-1688.2011.00544.x

Perelman, L., and Ostfeld, A. (2010). "Bayesian networks for estimating contaminant source and propagation in a water distribution system using cluster structure." Proceedings of the 12th Annual Conference on Water Distribution Systems Analysis, Tucson, A.Z., U.S., pp. 426-435.

Prochazka, A., Vyšata, O., Vališ, M., Ťupa, O., Schätz, M., and Mařík, V. (2015). "Bayesian classification and analysis of gait disorders using image and depth sensors of Microsoft Kinect." Digital Signal Processing, Elsevier, Vol. 47, pp. 169-177. 10.1016/j.dsp.2015.05.011

Puga, J.L., Krzywinski, M., and Altman, N. (2015). "Points of significance: Bayes' theorem." Nature Methods, Nature Publishing Group, Vol. 12, No. 4, pp. 277-278. 10.1038/nmeth.333526005726

Raftery, A.E., Gneiting, T., Balabdaoui, F., and Polakowski, M. (2005). "Using Bayesian model averaging to calibrate forecast ensembles." Monthly Weather Review, AMS, Vol. 133, No. 5, pp. 1155-1174. 10.1175/MWR2906.1

Reis Jr., D.S., and Stedinger, J.R. (2005). "Bayesian MCMC flood frequency analysis with historical information." Journal of Hydrology, Elsevier, Vol. 313, No. 1, pp. 97-116. 10.1016/j.jhydrol.2005.02.028

Seo, D.J., and Smith, J.A. (1991). "Rainfall estiation using raingages and radar - a Bayesian approach: 1. Derivation of estimators." Stochastic Hydrology and Hydraulics, Springer, Vol. 5, No. 1, pp. 17-29. 10.1007/BF01544175

Shenton, W., Hart, B.T., and Chan, T.U. (2014). "A Bayesian network approach to support environmental flow restoration decisions in the Yarra River, Australia." Stochastic Environmental Research and Risk Assessment, Springer, Vol. 28, No. 1, pp. 57-65. 10.1007/s00477-013-0698-x

Shin, J.Y., Ajmal, M., Yoo, J., and Kim, T.W. (2016). "A Bayesian network-based probabilistic framework for drought forecasting and outlook." Advances in Meteorology, Hindawi, London, UK. 10.1155/2016/9472605

Smith, M. (2006). "Dam risk analysis using Bayesian networks." Proceedings of Geohazard, Engineering Conference International, Lillehammer, Norway.

Smith, T.J., and Marshall, L.A. (2008). "Bayesian methods in hydrologic modeling: A study of recent advancements in Markov chain Monte Carlo techniques." Water Resources Research, Wiley, Vol. 44, No. 12, W00B05. 10.1029/2007WR006705

Stedinger, J.R., and Kim, Y.O. (2010). "Probabilities for ensemble forecasts reflecting climate information." Journal of Hydrology, Elsevier, Vol. 391, No. 1-2, pp. 9-23. 10.1016/j.jhydrol.2010.06.038

Tajiki, M., Schoups, G., Hendricks Franssen, H.J., Najafinejad, A., and Bahremand, A. (2020). "Recursive Bayesian estimation of conceptual rainfall‐runoff model errors in real‐time prediction of streamflow." Water Resources Research, Wiley, Vol. 56, No. 2, WR025237. 10.1029/2019WR025237

Tang, Y., Marshall, L., Sharma, A., and Smith, T. (2016). "Tools for investigating the prior distribution in Bayesian hydrology." Journal of Hydrology, Elsevier, Vol. 538, pp. 551-562. 10.1016/j.jhydrol.2016.04.032

Thiemann, M., Trosset, M., Gupta, H., and Sorooshian, S. (2001). "Bayesian recursive parameter estimation for hydrologic models." Water Resources Research, Wiley, Vol. 37, No. 10, pp. 2521-2535. 10.1029/2000WR900405

Thyer, M., Renard, B., Kavetski, D., Kuczera, G., Franks, S.W., and Srikanthan, S. (2009). "Critical evaluation of parameter consistency and predictive uncertainty in hydrological modeling: A case study using Bayesian total error analysis." Water Resources Research, Wiley, Vol. 45, No. 12, W00B14. 10.1029/2008WR006825

Vicens, G.J., Rodriguez-Iturbe, I., and Schaake Jr, J.C. (1975a). "A Bayesian framework for the use of regional information in hydrology." Water Resources Research, Wiley, Vol. 11, No. 3, pp. 405-414. 10.1029/WR011i003p00405

Vicens, G.J., Rodríguez-Iturbe, I., and Schaake Jr, J.C. (1975b). "Bayesian generation of synthetic streamflows." Water Resources Research, Wiley, Vol. 11, No. 6, pp. 827-838. 10.1029/WR011i006p00827

Viglione, A., Merz, R., Salinas, J.L., and Blöschl, G. (2013). "Flood frequency hydrology: 3. A Bayesian analysis." Water Resources Research, Wiley, Vol. 49, No. 2, pp. 675-692. 10.1029/2011WR010782

Vrugt, J.A., Ter Braak, C.J., Gupta, H.V., and Robinson, B.A. (2009). "Equifinality of formal (DREAM) and informal (GLUE) Bayesian approaches in hydrologic modeling?" Stochastic Environmental Research and Risk Assessment, Springer, Vol. 23, No. 7, pp. 1011-1026. 10.1007/s00477-008-0274-y

Wellen, C., Arhonditsis, G.B., Long, T., and Boyd, D. (2014). "Accommodating environmental thresholds and extreme events in hydrological models: A Bayesian approach." Journal of Great Lakes Research, Elsevier, Vol. 40, pp. 102-116. 10.1016/j.jglr.2014.04.002

Yang, J., Reichert, P., and Abbaspour, K.C. (2007). "Bayesian uncertainty analysis in distributed hydrologic modeling: A case study in the Thur River basin (Switzerland)." Water Resources Research, Wiley, Vol. 43, No. 10, W10401. 10.1029/2006WR005497

Zhang, X., Liang, F., Yu, B., and Zong, Z. (2011). "Explicitly integrating parameter, input, and structure uncertainties into Bayesian neural networks for probabilistic hydrologic forecasting." Journal of Hydrology, Elsevier, Vol. 409, No. 3-4, pp. 696-709. 10.1016/j.jhydrol.2011.09.002

Zhang, X., and Zhao, K. (2012). "Bayesian neural networks for uncertainty analysis of hydrologic modeling: A comparison of two schemes." Water Resources Management, Springer, Vol. 26, No. 8, pp. 2365-2382. 10.1007/s11269-012-0021-5

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Development of the Bayesian method and its application to the water resources field

ABSTRACT

MAIN

(1)

Fig. 1

Bayesian framework

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Fig. 2

Types of applying the Bayesian method in the water resources field

Fig. 3.

Bayesian framework for flood frequency analysis with the spatiotemporal expansion of data (Viglione et al., 2013)

(10)

(11)

Fig. 4

Derivation of the posteriori distribution with the BMA for weather forecasting (Raftery et al., 2005)

(12)

(13)

(14)

Fig. 5

Bayesian methods used for uncertainty analysis

(15)

(16)

(17)

(18)

(19)

(20)

Acknowledgements

References