1. 서 론
2. 이론 고찰 및 분석방법
2.1 일유량의 수문학적 지속성
2.2 일유량의 대푯값
2.3 일 최빈유량을 이용한 유황곡선 작성방법
3. 분석지점 및 이용자료
3.1 분석지점
3.2 이용자료
4. 검토결과와 활용방안
4.1 일유량의 수문학적 지속성 검토결과
4.2 일 최빈유량의 대표성 검토
4.3 일 최빈유량의 내림차순곡선
4.4 일 최빈유량곡선의 활용방법
5. 결 론
1. 서 론
하천에서의 유량관리는 연중 일유량의 변화 즉, 유황(流況)을 안정시켜 홍수조절, 갈수관리, 이수적 이용, 수질 및 생태를 보전하기 위한 것이므로 유황분석은 매우 중요하다. 대표적인 유황분석 방법으로는 유황곡선이 이용되고 있다. 유황곡선은 1880년 Clemens Herschel에 의해 처음으로 도입된 개념으로서(Fennessey and Vogel, 1990) 하천 임의지점에서 특정 유량값 이상인 일유량이 연중 며칠 이상 지속되는가를 파악하기 위한 일유량의 변화곡선이다.
유황곡선은 1년 중 해당 유량 이상이 발생되는 일수에 따라 갈수유량(Q355, 355일), 저수유량(Q275, 275일), 평수유량(Q185, 185일), 풍수유량(Q95, 95일), 홍수유량(Q10, 10일)을 기준유량으로 설정하고, 이들의 회귀곡선을 이용하여 작성한다. 이러한 방법은 개념적으로 쉽게 이해될 수 있으며, 수년(water year)의 주기성이 반영되기 때문에 매우 유용하게 이용되고 있다(Lee et al., 1993). 홍수유량의 지속일수를 1일로 보아 최대유량(Q1, 1일)을 홍수유량으로 판단하는 경우도 있으나 본 연구에서는 유황계수에서 사용한 것과 같이 지속일수 355일에 해당하는 갈수유량과 대비되는 지속일수 10일에 해당하는 유량으로서의 홍수유량에 대한 정의가 필요하다는 점에서 지속일수 10일에 해당하는 유량을 홍수유량(Q10, 10일)으로 정의하였다.
유황곡선을 이용하면 최소유량에서 최대유량에 이르는 일유량의 연중 변화양상뿐만 아니라 일별 ‧ 월별 ‧ 계절별 유량의 변화특성도 파악할 수 있다. 또한, 유황곡선은 상류의 댐 건설로 인한 하류의 유황개선효과 분석, 연간 총 유출량의 변화 등 유량변동 파악, 특정유량의 공급가능기간과 사용가능 수량 산정 등 수력에너지의 개발가능성 판단, 저수시설 없이 취수 가능한 유량의 규모와 변동성 등 저수지 축조 여부 판단, 관개계획의 수립, 비유량법을 이용한 다른 하천과의 유황 비교, 하천기본계획 수립에의 활용 등 매우 다양하게 이용할 수 있다. 현재 실무에서는 10년 정도의 일유량 자료를 이용하여 연중의 유황변화를 분석하고 있다.
Park (1974)은 유역특성인자와 갈수유량 ‧ 홍수유량과의 관계를 분석하였고, Lee (1994)는 지속일수를 기준으로 유황을 구분하였으며, Shin (2000)은 기후변화에 따른 안동댐 유역의 수문응답 변화양상을 수치적으로 모의하여 유황의 변화를 전망하였다. Park (2003)은 유역의 지상학적 인자와 기후학적 인자를 이용하여 자연하천에 대한 무차원 유황곡선을 제안하였다. Jung and Yoon (2003)은 유황곡선을 얻을 수 있는 간략식을 제안하였고, Ahn et al. (2005)은 댐 건설 전후의 유황곡선을 비교하여 댐 건설로 인한 유황의 안정화 방안을 제시하였다. Ha et al. (2012)은 수위-유량관계를 이용하여 섬진강 수계의 유황을 분석하였다.
기존의 유황곡선은 매년의 일유량을 크기순으로 내림차순한 후, 동일 순위별로 분석기간 동안의 일유량을 산술평균하여 가로축은 지속시간(일), 세로축은 대수 일유량(m3/sec)으로 하여 도시한 후, 이를 회귀분석한 식을 이용하고 있다. 그러나 기존의 유황곡선은 다양한 활용성에도 불구하고 다음과 같은 몇 가지 문제점이 있다. 첫째, 개념적 측면에서는 매년의 일유량을 크기순으로 내림차순하여 동일 순위별로 산술평균하기 때문에 큰 유량은 크게, 작은 유량은 작게 지속되려는 성질인 일유량의 수문학적 지속성을 고려하지 않고 있다. 둘째, 작성방법 측면에서는 동일 순위별로 분석기간(년) 동안의 최대유량이나 최소유량을 모두 반영하여 산술평균하기 때문에 일유량의 왜곡이 발생하고 있다. 셋째, 활용성 측면에서는 일유량의 발생순서를 고려하지 않기 때문에 특정유량의 발생시점이나 지속기간을 알 수 없다. 이러한 문제점들로 인해 저수유량(Q275) 이하와 풍수유량(Q95) 이상에서 유황곡선의 기울기가 급변하고, 매년의 유황변동 폭이 커서 이용에 어려움이 따르는 것으로 알려져 있다(Park, 2003).
따라서, 본 연구에서는 이러한 기존 유황곡선의 문제점들을 개선하기 위해 매년의 일유량을 발생일자별로 정렬한 후, 일별로 일 최빈유량을 산정하고, 이들을 5일 단위로 평균하여 나타내는 일 최빈유량곡선법이라는 유황곡선 개선방안을 제시한다.
2. 이론 고찰 및 분석방법
2.1 일유량의 수문학적 지속성
기존의 유황곡선은 일유량이 무작위하게 발생한다는 가정에 의한 것이어서 일유량이 수문학적 지속성이 있다고 판단되면 개선되어야 한다. 수문학적 지속성이란 짧은 기간(시간 또는 일 단위) 동안에 큰 값은 크게 작은 값은 작게 지속되려는 성질을 의미한다. 본 연구에서는 무작위성 검정방법의 하나인 “Anderson Exact 검정”을 이용하여 95% 신뢰구간에서 일유량의 수문학적 지속성 여부를 판단한다. 이 방법에서는 자료 수가 n인 자료계열에서 Eq. (1)과 같은 “1차 계열 상관계수(Lag-One Serial Correlation Coefficient)”를 r로 정의한다(Anderson, 1942).
여기서, n은 유량계열 Q의 자료 수, 는 평균, Co는 0차 계열 공분산(Serial Covariance), C1은 1차 계열 공분산이고, 이면 무작위성 시계열, 이면 지속성이 강한 시계열임을 의미한다. Eq. (1)의 상관계수 값이 Eq. (2)의 범위를 벗어나면 지속성이 있는 계열로 간주한다.
상관계수 값이 어느 정도 이상이어야 상관성이 있는지에 대한 명확한 기준은 없으나 통계학에서는 Table 1과 같이 상관계수가 0.5 이상이면 상관성이 있다고 판단한다(Seong, 2012).
Table 1.
Degrees of correlation coefficient
| Degree | Very Weak | Weak | Moderate | Strong | Very Strong |
| Value | 0.0 (None) ~ 0.2 | 0.2 ~ 0.4 | 0.4 ~ 0.6 | 0.6 ~ 0.8 | 0.8 ~ 1.0 (Perfect) |
2.2 일유량의 대푯값
기존의 유황곡선은 매년의 일유량을 크기순으로 내림차순한 후, 동일 순위별로 산술평균한다. 이때 동일 순위마다 분석기간(년)과 동일한 개수의 일유량 자료계열이 형성되고, 이를 모두 산술평균하기 때문에 최대유량이나 최소유량으로 인한 일유량의 왜곡이 발생한다. 이러한 왜곡을 완화하기 위해서는 최대유량이나 최소유량을 포함하지 않으면서도 해당 순위의 일유량을 적절히 대표할 수 있는 대푯값을 선정할 필요가 있다.
통계학에서 주로 사용되는 자료계열의 대푯값으로는 산술평균(Arithmetic Mean), 중앙값(Median), 절사평균(Trimmed Mean), 최빈값(Mode) 등이 있다. 산술평균은 자료계열의 합을 자료수로 나눈 값으로서 극단값들로 인한 왜곡이 발생한다. 중앙값은 자료계열을 크기 순으로 내림차순했을 때 중앙에 위치하는 값으로서 극단값들의 영향을 받지는 않으나 하나의 중앙값만으로 계산되는 것이 문제이다. 절사평균은 전체 자료계열 중 일정 비율 이내의 자료값만으로 구한 평균값으로서 극단값들을 제외할 수는 있으나 극단값들을 제외하기 위한 적정 비율을 결정하기 어렵다는 점이 문제이다. 최빈값은 자료계열에서 가장 빈번하게 발생되는 자료값으로서 가장 빈번하게 발생하는 자료 값을 선정할 수 있으나 최빈값에 포함되지 않은 자료들이 무시된다는 것이 단점이다. 이처럼 방법마다 장 ‧ 단점이 있으나 최빈값(일 최빈유량)은 자료기간 동안 해당 일자에서 가장 빈번하게 발생하는 유량이며, 상 ‧ 하위의 극단적 유량값들을 제외시킬 수 있다는 점에서 다른 방법들보다는 합리적인 방법이라고 사료된다. 분석기간 동안의 일유량 자료로부터 매년의 일자별 일 최빈유량을 산정하는 방법은 Table 2와 같다.
Table 2.
Daily mode discharge calculation procedure
2.3 일 최빈유량을 이용한 유황곡선 작성방법
앞에서 고찰한 기존 유황곡선 작성방법의 문제점과 대안을 종합해 보면 다음과 같다. 첫째, 개념적 측면에서 매년의 일유량을 크기순으로 내림차순하여 동일 순위별로 정렬하면 일유량의 수문학적 지속성을 고려하지 못하므로 매년의 일유량을 발생일자별로 정렬하는 방식으로 개선하여야 한다. 둘째, 작성방법 측면에서 자료기간 동안의 매년의 일유량을 발생일자별로 정렬하더라도 해당 일자의 모든 유량자료를 산술평균하면 최대유량이나 최소유량 등이 포함되어 일유량이 왜곡될 수 있다. 따라서 발생일자별 산술평균보다는 발생일자별 일 최빈유량을 이용하면 이러한 왜곡을 완화할 수 있다. 일 최빈유량은 자료기간 동안 해당 일자에서 가장 빈번하게 발생되는 유량이고, 최대유량이나 최소유량과 같은 상‧하위의 극단적인 유량값들을 제외시킬 수 있다. 셋째, 활용성 측면에서 특정 크기의 유량이 발생되는 시점이나 지속기간을 파악하기 위해서는 매년의 일유량을 발생일자별로 정렬할 필요가 있다.
본 연구에서는 이러한 시사점들을 종합하여 매년의 일유량을 발생일자별로 정렬한 후, 발생일자별 일 최빈유량을 대푯값으로 하는 일 최빈유량곡선법을 제시하고자 한다. 유황분석 기준유량도 각각의 지속일수에 해당하는 일 최빈유량으로 정의하고자 한다. Table 3에는 기존 유황곡선과 일 최빈유량곡선을 비교하여 제시하였으며, 주요 내용은 다음과 같다. 첫째, 자료기간 동안의 매년의 일유량을 동일한 일자별로 정렬한다. 이때 자료의 일관성을 확보하기 위해 4년마다 한 번씩 발생하는 2월 29일의 일유량 자료는 제외한다. 둘째, Table 2에 제시한 절차에 따라 발생일자별 일 최빈유량을 산정한다. 일 최빈유량을 산정하기 위한 자료계열의 적절한 등급구간의 수는 통계학에서 이용되고 있는 Eq. (3)과 같은 Huntsberger (1961) 공식과 Eq. (4)와 같은 Brooks and Carruthers (1953) 공식을 이용하여 결정한다.
Table 3.
Comparison of conventional flow duration curve and daily mode discharge curve
여기서, k는 등급구간의 수이고, N은 분석기간의 수(년)이다. 본 연구에서의 분석기간은 분석지점에 따라 13 ~ 30년인데 분석기간이 30년이면 Huntsberger 공식으로는 5.9개, Brooks C. and Carruthers 공식으로는 7.4개이고, 분석기간이 13년이면 Huntsberger 공식으로는 4.7개, Brooks C. and Carruthers 공식으로는 5.6개 정도로 구분하는 것이 적절한 것으로 나타나 본 연구에서는 6개 등급구간으로 구분하였다. 특정일자에 복수의 등급구간에서 최빈값이 발생할 경우에는 안정적 유량 확보라는 관점에서 낮은 등급구간의 일 최대유량을 해당 일의 일 최빈유량으로 선정하였다. 셋째, 선정된 일 최빈유량들을 5일 단위로 평균하여 5일 평균 최빈유량을 산정한다. 5일 평균을 채택하는 이유는 매일의 일유량은 변동이 심하여 어느 정도의 평균적 개념이 필요하고, 유황분석 기준유량들이 5일 단위로 구분되며, 1년이 5일씩 73개 구간으로 구분되는 등 기간구분을 위한 최소단위로 5일이 적정하다고 사료되기 때문이다. 넷째, 5일 평균 일 최빈유량을 가로축은 연중 발생일(일), 세로축은 대수 일유량(logQ)으로 하여 그래프로 나타내면 일 최빈유량곡선이 된다. 이러한 일 최빈유량곡선을 이용하면 특정유량의 발생일자뿐만 아니라 지속기간도 손쉽게 파악할 수 있으며, 특정일자의 일 최빈유량이 어떤 유황분석 기준유량보다 얼마나 크고 작은지도 파악할 수 있다.
3. 분석지점 및 이용자료
3.1 분석지점
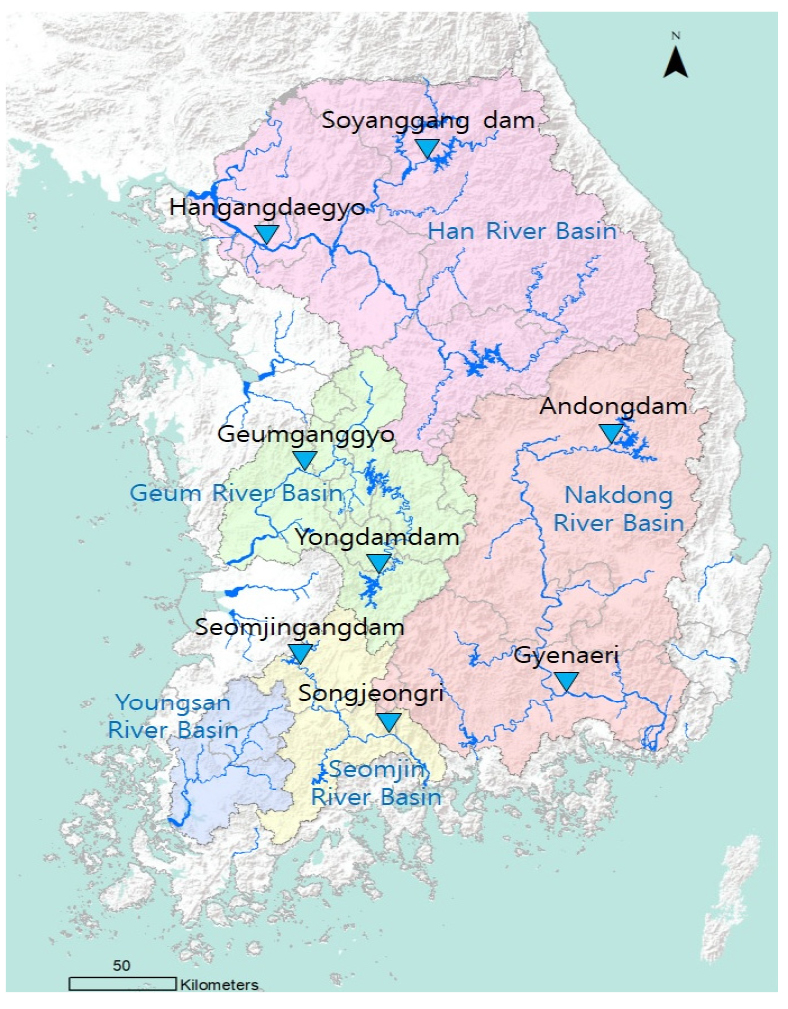
분석지점은 다음과 같은 몇 가지를 고려하여 선정하였다. 첫째, 장기간 지속적으로 일유량을 관측하고 있는 지점, 둘째, 일유량의 연중 변화특성을 잘 파악할 수 있는 지점, 셋째, 분석결과의 일반성을 확보하기 위해 자연상태에 가까운 상류지점과 하천으로의 유입 ‧ 방류 ‧ 저류 ‧ 취수와 같은 물이용이 이루어지고 있는 하류지점 등이다. 이러한 선정관점들을 고려하여 4대강(한강, 낙동강, 금강, 섬진강) 본류의 상류 4개 지점(소양강댐, 안동댐, 용담댐, 섬진강댐)과 하류 4개 지점(한강대교, 계내리, 금강교, 송정리) 등 총 8개 지점을 선정하였다. 상류지점들은 다목적댐이 위치하고 있어 상류유역의 개발이 적고, 인위적인 유입 ‧ 방류 ‧ 저류 ‧ 취수가 적어 비교적 자연상태에 가까운 지점들이다. 하류지점들은 유량이 풍부하고, 하천수 이용량이 많아 하천관리상 중요한 지점들이다. 분석지점의 위치도는 Fig. 1에 나타내었다.
3.2 이용자료
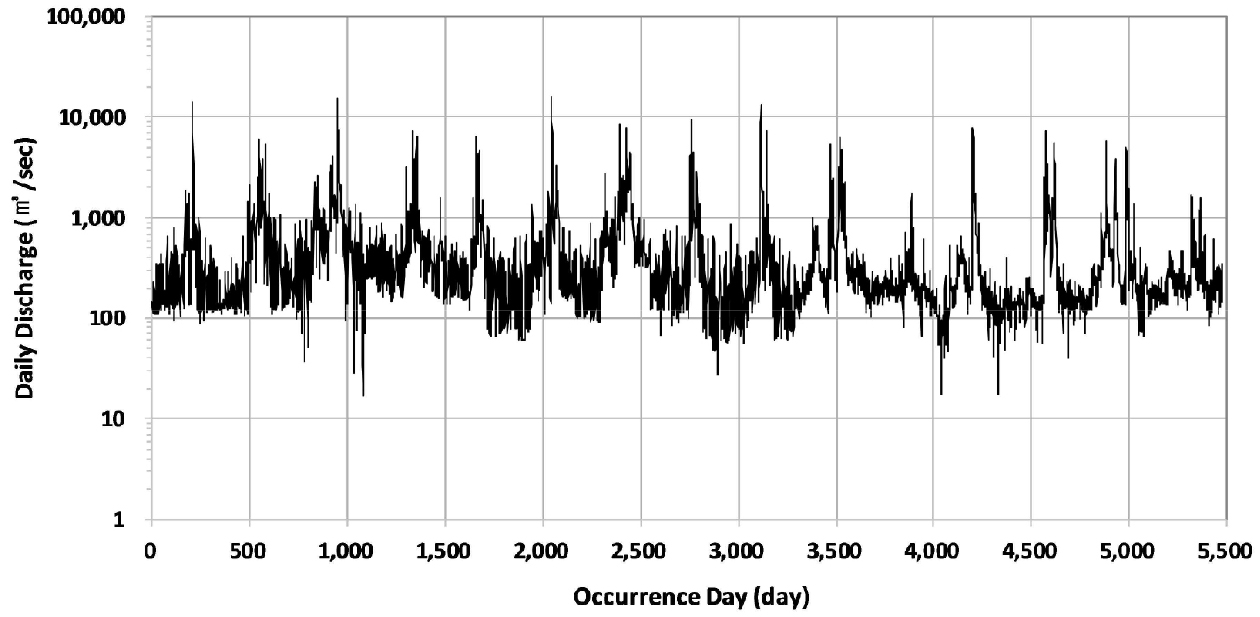
본 연구에서는 분석의 신뢰성을 제고하기 위해 국가수자원관리 종합정보시스템에서 제공하는 장기간의 관측 일유량을 이용하였다. 4개 댐 상류지점의 일유량은 댐수위와 방류량을 이용하여 역산한 일평균 유입량이다. 4개 하류지점 중 섬진강 송정리 지점의 일유량은 수위-유량관계식을 이용하여 산정한 유량이며, 한강대교, 계내리, 금강교 지점의 일유량은 도플러 방식의 초음파 유속계를 이용하여 실시간으로 자동측정한 유량이다. 또한, 하류지점은 비교적 유량이 풍부한 본류 하류라는 점과 결측유량을 보완하여 이용할 경우, 분석결과의 신뢰성에 영향을 미칠 수 있기 때문에 영(0)유량 포함연도와 결측일 포함년도의 모든 일유량 자료를 제외하였다. Table 4에는 분석지점별 개요와 분석자료의 통계적 특성을 제시하였고, Fig. 2에는 한강대교 지점의 분석기간 동안의 일유량 변화 그래프를 사례로 제시하였다.
Table 4.
Overview and statistical characteristics of analysis points
4. 검토결과와 활용방안
4.1 일유량의 수문학적 지속성 검토결과
Eqs. (1) and (2)를 이용하여 분석지점별 일유량의 수문학적 지속성을 검토한 결과, Table 5에서 보는 바와 같이 8개 지점 모두에서 Eq. (1)에 의한 상관계수 값이 Eq. (2)의 범위를 벗어났으며, 그 값도 0.5 이상으로 나타나 일유량의 수문학적 지속성이 높은 것으로 나타났다. 따라서, 현재의 유황곡선 작성방법은 수문학적 지속성을 고려하여 매년의 일유량을 발생일자별로 정렬하는 방식으로 개선되어야 할 것으로 나타났다.
Table 5.
Result of the hydrologic persistence analysis
4.2 일 최빈유량의 대표성 검토
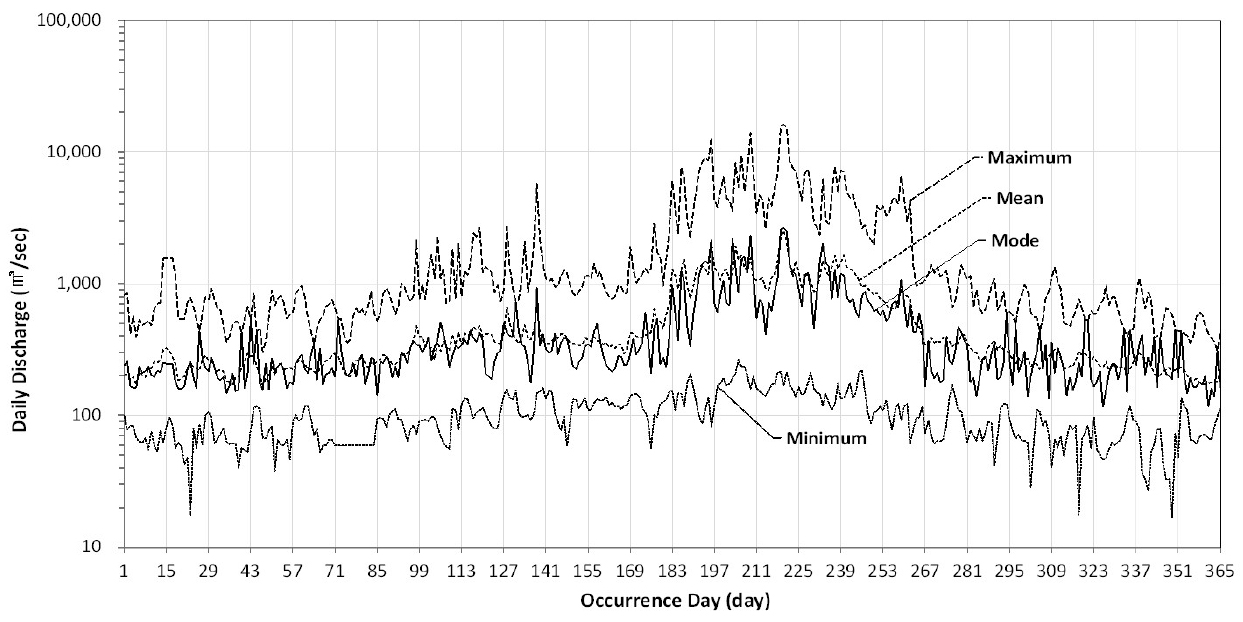
Table 2의 절차에 따라 산정한 분석지점별 일 최빈유량과 일 최대유량, 일 평균유량, 일 최소유량과의 상관성을 검토한 결과, Table 6에서 보는 바와 같이 안동댐 지점이나 섬진강댐 지점 등 일부 지점에서 일 최소유량과 일 최빈유량과의 상관계수가 낮게 나타난 것을 제외하고는 일 최빈유량과 일 평균유량 및 일 최대유량과의 상관계수가 높게 나타나 해당 일자의 일 최빈유량이 해당 일자의 일유량을 대표하는데 무리가 없는 것으로 사료된다. 따라서 본 연구에서는 일 최빈유량을 이용한 유황곡선 작성방법을 제시함으로써 자료기간 동안의 모든 일유량을 산술평균함에 따른 일유량의 왜곡을 완화하고자 한다. Fig. 3에는 한강대교 지점에서의 일 최빈유량과 일 최대유량, 일 평균유량, 일 최소유량의 변화 그래프를 사례로 제시하였다.
Table 6.
Correlation coefficient with daily mode discharge
4.3 일 최빈유량의 내림차순곡선
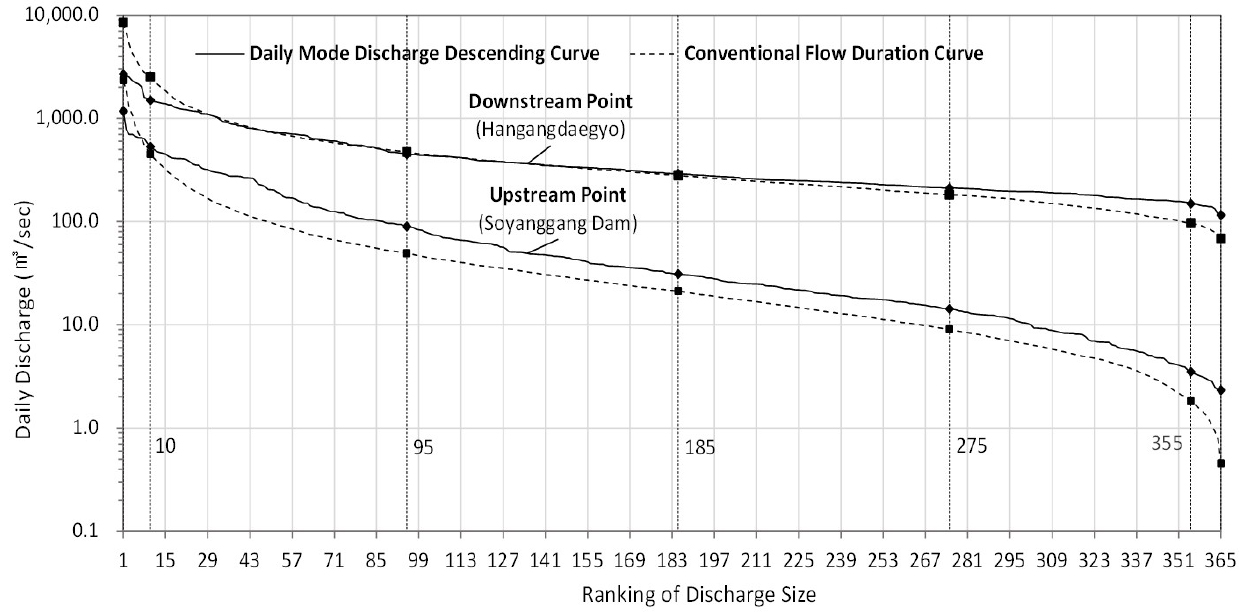
앞에서 고찰한 바와 같이 일 최빈유량을 이용하면 일유량의 산술평균에 따른 왜곡을 완화할 수 있다. Table 2의 절차에 따라 자료기간 동안의 일자별 일 최빈유량을 산정한 후, 이를 내림차순한 곡선과 기존 유황곡선을 비교하였다. 비교결과, Table 7에서 보는 바와 같이 일 최빈유량의 내림차순곡선은 기존 유황곡선보다 전반적으로 풍수유량(Q95) 이상과 저수유량(Q275) 이하에서의 기울기가 완만해져 이들 구간에서 유황곡선의 기울기가 급변하는 문제점이 개선되는 것으로 나타났다. Fig. 4에는 한강 본류 상 ‧ 하류에 위치한 소양강댐 지점과 한강대교 지점에서의 일 최빈유량의 내림차순곡선과 기존의 유황곡선을 비교한 그래프를 사례로 제시하였다.
Table 7.
Relative error between daily mode discharge descending curve and conventional flow duration curve (Unit : m3/sec)
4.4 일 최빈유량곡선의 활용방법
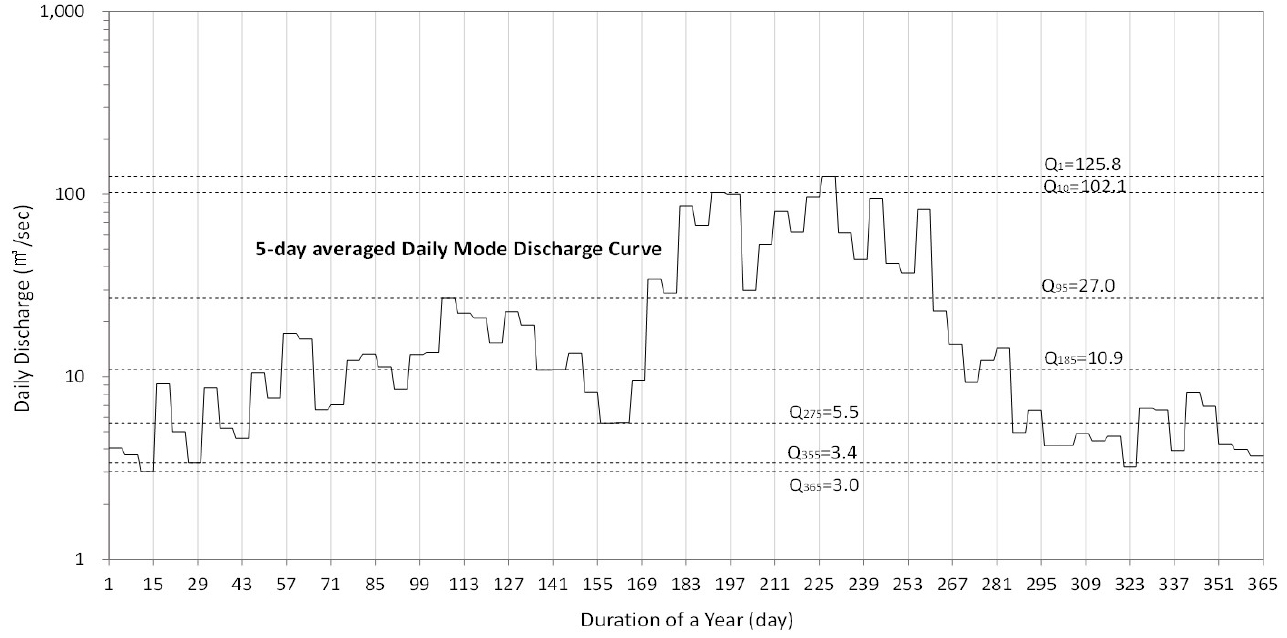
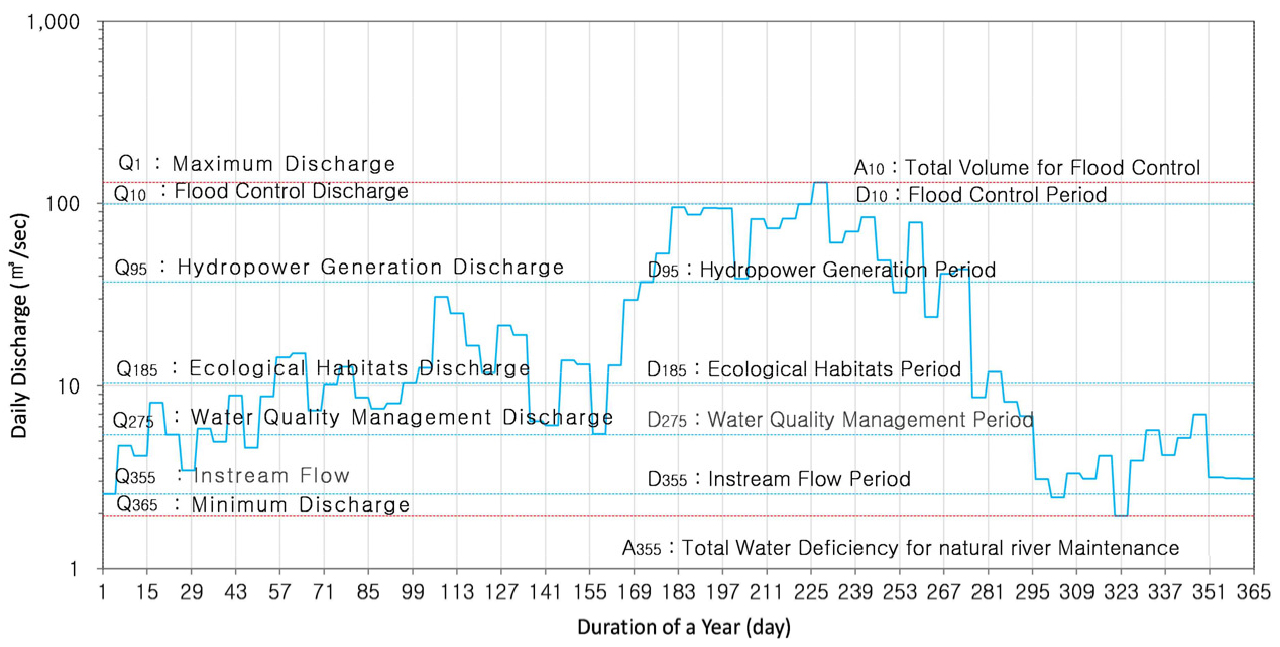
Fig. 5에는 이상의 방법으로 작성한 용담댐 지점에서의 일 최빈유량곡선을 사례로 나타내었다. 일 최빈유량곡선은 Fig. 6의 활용개념도에 나타낸 바와 같이 특정유량의 발생시점이나 연중 지속기간을 손쉽게 파악할 수 있을 뿐만 아니라 유황분석 기준유량별로 다양하게 활용할 수 있다. Vogel and Fennessey (1995)는 유황곡선이 수력발전, 홍수조절, 수질관리, 유사(流沙), 용수 이용 등과 관련이 있음을 제시하였다. 다만, 어떠한 유황분석 기준유량을 어떠한 목적에 활용하는 것이 적절한 것인지에 대해서는 분야별로 지속적인 연구가 이루어지고 있으므로 본 연구에서 논하지 않는다.
갈수유량(Q355)을 하천수 사용허가유량과 허가기간을 판단하기 위한 기준유량으로 이용할 경우, 갈수유량 이상의 유량이 발생하는 기간의 합(D355)은 하천유지유량을 확보할 수 있는 기간이고, 갈수유량 아랫부분의 면적(A355)은 하천유지유량을 확보하기 위해 추가로 필요한 유량의 총량을 의미한다. 저수유량(Q275)을 생물학적 산소요구량(BOD)을 산정하는 기준유량으로 이용할 경우, 저수유량 이상의 유량이 발생하는 기간의 합(D275)은 목표수질관리가 가능한 기간이고, 저수유량 아랫부분의 면적은 목표수질을 달성하기 위해 추가로 확보해야 하는 유량의 총량을 의미한다. 평수유량(Q185)을 하천생태계의 유지 가능성을 판단하는 기준유량으로 이용할 경우, 평수유량 이상의 유량이 발생되는 기간의 합(D185)은 하천생태계를 유지할 수 있는 기간을 의미한다. 풍수유량(Q95)을 수력발전의 가능성을 판단하는 기준유량으로 이용할 경우, 풍수유량 이상의 유량이 발생되는 기간의 합(D95)은 안정적으로 수력발전 할 수 있는 기간을 의미한다. 홍수유량(Q10)을 홍수조절의 필요성 여부를 판단하는 기준유량으로 이용할 경우, 홍수유량 이상의 유량이 발생되는 기간의 합(D10)은 홍수조절이 필요한 기간이 되고, 홍수유량 윗부분의 면적(A10)은 홍수조절이 필요한 유량의 총량을 의미한다.
5. 결 론
기존의 유황곡선은 높은 활용성에도 불구하고 일유량의 크기 순 내림차순 정렬, 동일 순위별 모든 일유량의 산술평균에 따른 일유량의 왜곡, 특정유량의 발생시점 및 지속시간 파악 불가 등의 문제점이 있다. 본 연구에서는 이러한 문제점들을 개선하기 위해 일자별 일 최빈유량을 산정하여 동일 일자별로 정렬한 후, 이를 5일 단위로 평균하여 도시하는 일 최빈유량곡선법을 제안하였고, 4대강(한강, 낙동강, 금강, 섬진강) 본류의 상류 4개 지점과 하류 4개 지점의 장기간 관측 일유량을 이용하여 그 적용 가능성을 검토하였다.
본 연구의 주요 결론은 다음과 같다. 첫째, 8개 지점 모두에서 일유량은 수문학적 지속성을 가지는 것으로 나타났다. 둘째, 일 최빈유량은 최대유량이나 최소유량과 같은 극단적인 유량값의 영향을 배제할 수 있고, 일 평균유량 및 일 최대유량과의 상관성도 높아 일별 유량특성을 대표하는데 무리가 없으며, 산술평균에 따른 일유량의 왜곡 문제도 완화할 수 있다. 셋째, 일 최빈유량의 내림차순곡선은 기존의 유황곡선보다 풍수유량 이상 및 저수유량 이하에서의 기울기가 완만하게 나타나 이들 구간에서 기울기가 급변하는 기존 유황곡선의 문제점을 개선할 수 있다. 넷째, 일 최빈유량곡선법은 일유량의 지속성을 확보할 수 있고, 유황분석 기준유량의 연중 초과 ‧ 미달 여부뿐만 아니라 특정유량의 발생시기와 지속기간도 손쉽게 파악할 수 있어 다양하게 이용할 수 있다.
본 연구에서는 4대강 본류 상 ‧ 하류 8개 지점에 대해서만 분석하였으나 연구결과의 일반성을 확보하고, 지점별 특성을 파악하기 위해서는 보다 많은 지점에 대한 분석이 이루어져야 할 것이다. 또한, 충분한 분석기간 동안 신뢰성 있는 일유량 자료를 안정적으로 확보하기 위해서는 결측유량의 원인별로 합리적인 보완방안이 마련되어야 한다. 아울러 유황분석 기준유량에 대한 하천관리상의 목적을 설정 ‧ 활용하기 위해서는 어떠한 유황분석 기준유량을 어떠한 관리목적에 활용하는 것이 적절한 것인지에 대한 지속적 연구와 논의가 이루어져야 할 것이다.