Numerical analysis of geomorphic changes in rivers due to dam pulse discharge of Yeongju Dam

Tae Hyo Baek; Chang-Lae Jang; Kyung Su Lee

doi:10.3741/JKWRA.2023.56.12.871

Preview

Research Article

Journal of Korea Water Resources Association. 31 December 2023. 871-881
https://doi.org/10.3741/JKWRA.2023.56.12.871

Numerical analysis of geomorphic changes in rivers due to dam pulse discharge of Yeongju Dam

댐 펄스방류로 인한 하천의 지형변화 수치모의 분석(영주댐 중심으로)

Tae Hyo Baek^a

Chang-Lae Jang^b

Kyung Su Lee^c^*

백 태효^a

장 창래^b

이 경수^c^*

^aPh.D Candidate, Department of Civil Engineering, Korea National University of Transportation, Chungju, Korea

^bProfessor, Department of Civil Engineering, Korea National University of Transportation, Chungju, Korea

^cResearch Officer, National Disaster Management Instiute, Ministry of the Interior and Safety, Ulsan, Korea

^a한국교통대학교 토목공학과 박사과정

^b국립한국교통대학교 건설환경도시교통공학부 사회기반공학전공 교수

^c행정안전부 국립재난안전연구원 시설연구사

^{*Corresponding Author}

ABSTRACT

This study investigates the geomorphic changes and Bed Relief Index of the river downstream of the Yeongju Dam by Nays2DH, a two-dimensional numerical model, in order to grasp the dynamics of the downstream river while applying various flow patterns such as pulse discharge. It shows that the geomorphic and the bed elevations changes are the largest under the condition of the normalized pulse discharge. The total change in the riverbed is 29.88 m for uniform flow, 27.46 m for normalized hydrograph, 29.63 m for pulse flow and 31.87 m for pulse flow with normalized hydrograph which result in the largest variation in scour and deposition. The Bed Relief Index (BRI) increases with time under conditions of uniform flow, pulse flow and pulse flow with normalized hydrograph. However, BRI increased rapidly until 30 hrs after the peak flow (14 hrs), but decreased from 56 hrs under the condition of normalized hydrograph. Therefore, the condition of normalized hydrograph gives greater dynamics than the condition of a single flood or constant flow, and the dynamics increase downstream than upstream, resulting in an effect on improving the environment of the river downstream of the dam.

Keywords

Yeongju Dam

River downstream of dam

Geomorphic Changes

Pluse Discharge

Discharge Normalization

국본 연구에서는 영주댐 하류 하천을 대상으로 2차원 수치모형인 Nays2DH를 적용하여 펄스방류 등 다양한 유량 조건에서 하류 하천의 역동성을 파악하기 위해 하도의 지형변화 특성 및 하상기복지수를 분석하였다. 수치모의에 적용되는 유량패턴은 등류 흐름, 정규화된 단일홍수, 펄스방류, 그리고 정규화된 펄스방류 등 4개의 유형이다. 수치모의 결과, 정규화를 적용한 펄스방류 조건일 때 하상고 및 하도의 변화가 가장 큰 것으로 나타났다. 총 하상 변화량은 등류 흐름 조건일 때 29.88 m, 정규화된 단일 홍수 조건일 때 27.46 m, 펄스 방류일 때 29.63 m 그리고 정규화된 펄스 방류일 때 31.87 m로이며, 이 조건에서 세굴과 퇴적의 변동 폭이 가장 크게 나타났다. 하상기복지수(BRI)를 분석한 결과, 등류 조건, 펄스방류, 그리고 정규화된 펄스방류 조건은 시간이 지날수록 BRI가 증가한다. 그러나, 정규화된 단일홍수에서는 첨두유량(14 hrs) 이후 30 hrs 까지 BRI가 급격하게 증가하지만, 그 이후부터는 증가 폭이 점점 감소하고, 56 hrs부터는 감소하였다. 수치모의가 끝날 때(72 hrs) BRI는 등류일 때 2.95, 정규화된 단일홍수일 때 3.31, 펄스방류일 때 3.34, 정규화된 펄스방류일 때 3.78이다. 따라서, 정규화된 펄스방류가 단일홍수나 등류보다 더 큰 역동성을 줄 수 있고, 하류로 갈수록 역동성이 커지면서 댐 하류하천의 환경개선에 효과를 가져올 수 있을 것으로 기대한다.

키워드

영주댐

댐 하류 하천

지형변화

펄스방류

유량정규화

MAIN

1. 서 론
2. 수치모형의 특징
3. 수치모형의 적용성 검토
3.1 펄스방류의 적용
3.2 수치모의 조건
3.3 수치모의 검증
4. 수치모의 결과
4.1 유량패턴에 따른 지형변화 분석
4.2 하상기복지수 분석
5. 결 론

1. 서 론

최근 기후변화로 인하여 홍수기에 집중호우가 발생하지만, 강수량이 감소하고 가뭄이 지속되고 있어 댐 운영을 통한 수자원 관리에 많은 어려움이 있다. 댐은 하천 종방향의 연속성을 교란하고, 유사이송과 흐름에 대한 연속성을 차단한다. 그리고 댐 상류에서는 하상고 상승으로 하상경사가 감소한다. 이는 저수지에 물이 유입될 때 이송능력을 현격하게 감소시킨다. 특히 댐 하류의 하천환경은 홍수의 규모, 유사의 공급, 하천 지류의 유량과 유사량에 의해 영향을 받는다(Williams and Wolman, 1984; Jang and Woo, 2009). 유사량의 감소는 저수지 저류량, 댐 운영, 댐의 위치에 따라 매우 다양하게 변한다(Brandt, 2000; Pitlick and Wilcock, 2001). Williams and Wolman (1984)은 미국 중부와 남서부의 21개 저수지에서 첨두홍수가 90%까지 감소했음을 확인하였고, Page et al. (2005)은 오스트레일라아 Murrumbidgee 강의 만재유량(bankfull discharge) 기간 및 빈도에 대하여 변화된 흐름을 분석한 결과 댐 건설 후 첨두홍수가 크게 감소했고 재현기간이 1.25년과 2년인 만제유량이 29~50% 감소하는 것을 확인하였다. 이렇게 댐 건설은 홍수의 크기와 빈도가 감소되고, 댐 상류에서부터 유사공급이 차단되어 하류 하천변화에 많은 영향을 준다. 특히 유량이 감소되면서 유사가 퇴적되어 육역화가 초래되고, 저수로가 분열하게 된다(Jang and Shimizu, 2010). 또한 댐에서 방류된 유량은 유사이송 에너지에 비해 소류사 농도가 매우 낮은 상태가 된다. 이러한 댐 하류역의 유사가 결핍된 유량(sediment starvation flow)은 하도의 세굴력을 증가시켜 하상세굴, 강턱침식 에너지를 소비하며, 연쇄적으로 하상저하를 유발하여 하상재료는 굵어진다. 이러한 과정은 평형상태에 도달하여 하상재료가 이동할 수 없거나 암반에 이르기까지 지속된다. 따라서 새로운 유사 공급이 없으면, 결국에는 여울과 소와 같은 중요 생물서식처가 소실되고, 하천구조물의 교각세굴, 해안선 후퇴와 같은 지형적 변화를 유발한다(Kondolf, 1997).

한국대댐회에 의하면 우리나라의 경우 전국 17,681개의 댐·저수지 중에서 1945년 이전에 건설되어 70년 이상 경과된 댐·저수지는 56.5%(9,558개소)이며, 50년이 경과된 댐·저수지는 87.9%(15,218개소)를 차지하여 노후화로 인한 저수지 퇴사에 따른 댐의 기능저하, 하류하천 환경과 생태계 미치는 영향은 점차 누적되어 가속화 되고 있다. 합천댐의 경우 댐 건설 이후 30년 동안 중앙입경(d50)은 1.0 mm에서 5.7 mm로 증가하며, 댐 하류 5 km까지는 장갑화현상(d50=2.16~44 mm)이 나타났다. 하상경사는 1/1,063에서 1/1,176으로 감소하였고 하상저하는 하류 20 km까지 평균 2.6 m 저하되었다. 수로 폭 또한 321 m에서 댐 건설 이후 172 m로 53% 감소했다(Shin and Julien, 2011). 이렇게 물리적으로 교란된 하천이 회복되는 데에는 긴 구간과 시간이 필요하다. 왜냐하면 세굴 및 지류에 의해 유입되는 유사량이 댐 건설 전의 유사량과 평형을 이루어야 하기 때문이다(Galay, 1983; Williams and Wolman, 1984).

댐에 의하여 유사가 차단된 하천에서 가장 일반적인 하류하천 복원 방법은 유사를 하천에 공급하는 것이다(Bunte, 2004). 최근 우리나라에서도 댐 하류하천의 환경을 개선하기 위하여 유사공급 방안을 계획하고 있다. 그중에서 댐·보·저수지에서 방류형식의 변화를 준 증가방류가 있다. 그러나, 증가방류는 하도에 미치는 영향이 작아, 하천의 역동적인 효과를 기대하기에는 어려움이 있기 때문에(Baek, 2020), 최근에는 동일한 유량으로 진동, 파동과 같은 파장 주기패턴을 적용한 펄스방류(flow pluses)가 시행되고 있다. 보 펄스 운영은 평소보다 많은 유량과 유사량을 방류하여 하류 유속을 증가시키고 수체 상하층간 혼합 유도 및 안정적인 유사공급을 통해 하천환경 개선을 도모하는 보 운영 방법으로 호주에서 제시되었다(NWC, 2009).

현재까지 댐하류 하천의 하상변화, 식생면적의 변화 등을 분석한 연구가 주를 이루고 있으나 펄스 방류에 대한 영향을 고려한 연구는 거의 없다. Jang and Woo (2009)는 대청댐 증가방류에 의한 댐 하류 하천의 물리적 특성을 수리학적으로 분석하였다. 댐 건설 직후 하상이 저하되고 저수로폭이 증가하지만, 일정 기간 이후부터는 큰 변화 없이 안정적으로 유지되었다. 그러나 하상토 입경은 증가하며, 표층의 조립화, 장갑층의 발달 등 장갑화 현상이 발생되는 것으로 나타났다. Shin and Julien (2011)에 의하면 펄스방류가 일반적인 정류 흐름보다 유사이송율이 21%높은 것으로 나타났다. Kang et al. (2016)은 영주댐 하류하천에서 유사공급에 의한 하도의 지형변화를 분석하였다. 시간이 지날수록 공급된 유사는 하류로 이동하며 하상고는 저하되고, 유속이 감소되는 하류지점에 퇴적된다. 시간이 증가하면서 하상고의 변화가 증가하고 하상의 역동성을 나타내는 하상기복지수가 증가하였으며, 특히 유량이 증가함에 따라 하상기복지수는 증가하였다. 따라서, 댐 하류 하천에서 토사공급에 의한 하도변화에 효과를 증가시키기 위해서는 댐에서 방류되는 유량을 증가시켜 하도의 역동성을 증가시켜야 한다고 제안하였다. 우리나라에서도 2015년 6월과 2016년 8월에 낙동강에서 녹조를 줄이기 위해 펄스방류를 실시하였지만, 녹조 저감효과 이외에 하도에 미치는 영향 및 효과는 분석하지는 않았다. 펄스방류는 단순히 유량을 증가하여 방류시키는 증가방류에 펄스패턴을 적용한 방식으로 하류하천의 하도 변화와 역동적인 효과를 예상할 수 있다.

본 연구에서는 2차원 수치모형인 Nays2DH를 이용하여 영주댐 하류 하천을 대상으로 펄스방류 등 다양한 유량패턴에 따른 하도의 지형변화를 예측하고 하천의 역동성 등 펄스방류의 효과를 분석하였다. 또한, 하상기복지수 분석을 통해 댐 하류 하천의 인위적인 교란을 저감하고, 하도의 역동성을 증가시키기 위한 하류 하천 관리방안을 제시하고자 하였다.

2. 수치모형의 특징

본 연구에서 적용된 Nays2DH 모형에서 지배방정식은 일반좌표계의 2차원 천수방정식을 적용하여 유속 및 수면의 변화를 나타내는 방식이다. 모형에 적용되는 지배방정식은 다음과 같다.

연속방정식

(1)

\frac{\partial}{\partial t} (\frac{h}{J}) + \frac{\partial}{\partial ξ} (\frac{h u^{ξ}}{J}) + \frac{\partial}{\partial η} (\frac{h u^{η}}{J}) = 0

운동량방정식

(2a)

\frac{\partial u^{ξ}}{\partial t} + u^{ξ} \frac{\partial u^{ξ}}{\partial ξ} + u^{η} \frac{\partial u^{ξ}}{\partial η} + α_{1} u^{ξ} u^{ξ} + α_{2} u^{ξ} u^{η} + α_{3} u^{η} u^{η} = - g [(ξ_{x}^{2} + ξ_{y}^{2}) \frac{\partial H}{\partial ξ} + (ξ_{x} η_{x} + ξ_{y} η_{y}) \frac{\partial H}{\partial η}] - C_{f} \frac{u^{ξ}}{h J} \sqrt{{(η_{y} u^{ξ} - ξ_{y} u^{η})}^{2} + {(- η_{x} u^{ξ} + ξ_{x} u^{η})}^{2}} + D^{ξ}

(2b)

\frac{\partial u^{η}}{\partial t} + u^{ξ} \frac{\partial u^{η}}{\partial ξ} + u^{η} \frac{\partial u^{η}}{\partial η} + α_{4} u^{ξ} u^{ξ} + α_{5} u^{ξ} u^{η} + α_{6} u^{η} u^{η} = - g [(η_{x} ξ_{x} + η_{y} ξ_{y}) \frac{\partial H}{\partial ξ} + (η_{x}^{2} + η_{y}^{2}) \frac{\partial H}{\partial η}] - C_{f} \frac{u^{η}}{h J} \sqrt{{(η_{y} u^{ξ} - ξ_{y} u^{η})}^{2} + {(- η_{x} u^{ξ} + ξ_{x} u^{η})}^{2}} + D^{η}

여기서, 𝜉, 𝜂는 일반좌표계의 공간좌표 성분이다. $u^{ξ}$ 와 $u^{η}$ 는 𝜉, 𝜂 방향의 유속(m/s), $J$ 는 Jacobian, $H$ 는 수위(m), $z_{b}$ 는 하상고(m), $C_{f}$ 는 하상전단응력계수이다. 운동량방정식에서 각 항의 매개변수 $α_{1} ~ α_{6}$ 는 다음과 같다.

(3a)

α_{1} = ξ_{x} \frac{\partial^{2} x}{\partial ξ^{2}} + ξ_{y} \frac{\partial^{2} y}{\partial ξ^{2}}, α_{2} = 2 (ξ_{x} \frac{\partial^{2} x}{\partial ξ \partial η} + ξ_{y} \frac{\partial^{2} y}{\partial ξ \partial η}), α_{3} = ξ_{x} \frac{\partial^{2} x}{\partial η^{2}} + ξ_{y} \frac{\partial^{2} y}{\partial η^{2}}

(3b)

α_{4} = η_{x} \frac{\partial^{2} x}{\partial ξ^{2}} + η_{y} \frac{\partial^{2} y}{\partial ξ^{2}}, α_{5} = 2 (η_{x} \frac{\partial^{2} x}{\partial ξ \partial η} + η_{y} \frac{\partial^{2} y}{\partial ξ \partial η}), α_{6} = η_{x} \frac{\partial^{2} x}{\partial η^{2}} + η_{y} \frac{\partial^{2} y}{\partial η^{2}}

운동량방정식의 확산항은 다음과 같다.

(4a)

D^{ξ} ≃ \frac{\partial}{\partial ξ} (ν_{t} ξ_{r}^{2} \frac{\partial u^{ξ}}{\partial ξ}) + \frac{\partial}{\partial η} (ν_{t} η_{r}^{2} \frac{\partial u^{ξ}}{\partial η})

(4b)

D^{η} ≃ \frac{\partial}{\partial ξ} (ν_{r} ξ_{r}^{2} \frac{\partial u^{η}}{\partial ξ}) + \frac{\partial}{\partial η} (ν_{t} η_{r}^{2} \frac{\partial u^{η}}{\partial η})

여기서, 와동점성계수 $ν_{t}$ 는 $k - ε$ 모형을 이용하여 해석하였다. 일반 좌표계에서 2차원 유사의 연속 방정식은 다음과 같다.

(5)

\frac{\partial}{\partial t} (\frac{z_{b}}{J}) + \frac{1}{1 - λ} [\frac{\partial}{\partial ξ} (\frac{q_{b}^{ξ}}{J}) + \frac{\partial}{\partial η} (\frac{q_{b}^{η}}{J})] = 0

여기서, $z_{b}$ 는 하상고(m), 𝜆는 하상재료의 공극률, $q_{b}^{ξ}$ 및 $q_{b}^{η}$ 는 각각 𝜉 와 𝜂 방향에서 단위 폭당 소류사량(m³/s/m)이다. 하상에서 소류사량은 Ashida and Michiue (1972)의 공식으로 계산하였다.

(6)

q_{b} = 17 τ_{*}^{3 / 2} (1 - \frac{τ_{* c}}{τ_{*}}) (1 - \frac{u_{* c}}{u_{*}}) \sqrt{S_{g} g d^{3}}

여기서 $q_{b}$ 는 소류사량(m³/s/m), $τ_{* c}$ 는 무차원 한계 소류력, $S_{g}$ 는 수중에서 하상재료의 비중, $g$ 는 중력가속도(m/s²), $d$ 는 소류사의 평균입경(mm), $u_{* c}$ 는 한계 마찰속도(m/s)이다.

하천에서 주 흐름 방향에 대한 횡단방향으로의 소류사 이송률을 계산하기 위하여, 원심력에 의한 이차류 및 횡방향 경사를 고려하였다. 𝜉 및 𝜂 방향에서 유사량은 Watanabe et al. (2001)이 제시한 방법을 사용하였으며, 다음과 같이 계산된다.

(7a)

q_{b}^{ξ} = q_{b} [\frac{u_{b}^{ξ}}{V_{b}} - γ (\frac{\partial z_{b}}{\partial ξ} + c o s θ \frac{\partial z_{b}}{\partial η})]

(7b)

q_{b}^{η} = q_{b} [\frac{u_{b}^{η}}{V_{b}} - γ (\frac{\partial z_{b}}{\partial η} + \cos θ \frac{\partial z_{b}}{\partial ξ})]

여기서 $u_{b}^{ξ}$ 및 $u_{b}^{η}$ 는 𝜉 및 𝜂 방향으로 하상부근에서 유속(m/s), $V_{b}$ 는 하상부근에서 유속(m/s), 𝜃는 𝜉 와 𝜂의 교차 각(°), 유사이송 보정계수 $γ = \sqrt{τ_{* c} / μ_{s} μ_{k} τ_{*}}$ 이며, 여기서 $μ_{s}$ 는 Coulomb의 정적 마찰계수(=1.0), $μ_{k}$ 는 Coulomb의 동적 마찰계수(=0.45)이다. 유선이 곡선형태로 굽어질 때, 원심력의 변화로 인한 이차류가 발생하며, 유선의 수직 방향에서 하상부근유속( $u_{b}$ )은 다음과 같다.

(8)

u_{b}^{n} = u_{b}^{s} N_{*} \frac{h}{r_{*}}

여기서, $r_{*}$ 는 유선의 곡률 반경(m), $N_{*}$ 는 이차류 강도 계수이다. $N_{*}$ 는 Engelund (1974)에 의한 제시된 7.0을 사용하였으며, 이는 만곡부에서 횡방향 경사가 완만한 상태에서 얻은 것으로써, 횡방향 경사가 급한 경우에 중력효과가 고려되어야 한다.

3. 수치모형의 적용성 검토

3.1 펄스방류의 적용

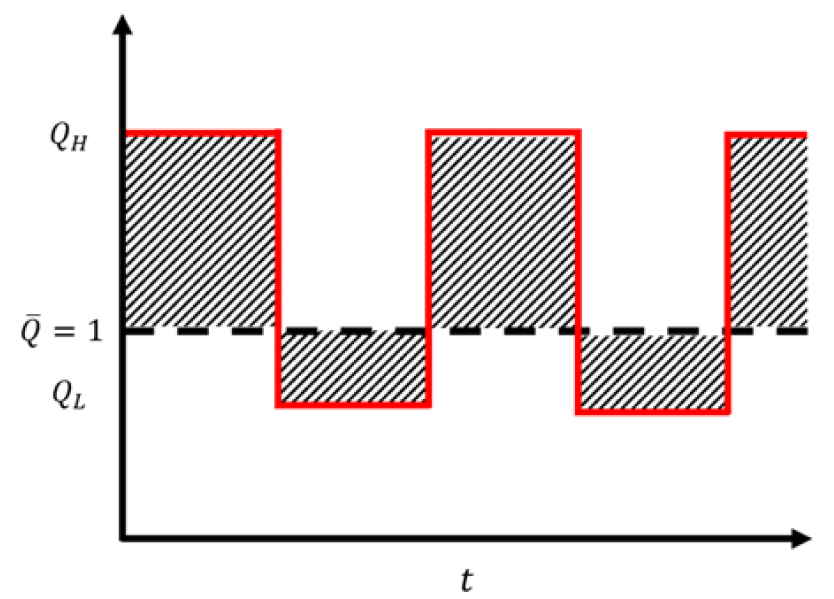
펄스방류는 진동, 파동과 같은 패턴의 수문곡선으로 유량을 방류하는 것을 말한다(Shin and Julien, 2011). 펄스방류는 지속시간 중에 첨두 펄스방류량( $Q_{H}$ ), 최소 펄스방류량( $Q_{L}$ ), 첨두유량의 지속시간 주기( $n$ -1)으로 구성된다. 평균 방류량은 다음과 같다.

(9)

\bar{Q} = Q_{L} (r + n - 1) / n

여기서, $\bar{Q}$ 는 평균 방류량(m³/s), $Q_{L}$ 는 최소 펄스방류량(m³/s), $r$ 은 토출비, $n$ 는 펄스주기이다. 토출비는 다음으로 정의한다.

(10)

r = Q_{H} / Q_{L}

여기서, $Q_{H}$ 는 최고 펄스방류량(m³/s), $Q_{L}$ 는 최소 펄스방류량(m³/s)이다. 펄스흐름이 없이 지속기간( $T$ )에 걸쳐 일정한 유량 $Q$ 가 흐를 경우, 이송된 유사량(부피)은 다음과 같다.

(11)

\bar{\forall_{s}} = a {\bar{Q}}^{b} T

Fig. 1은 펄스패턴의 유량 모식도이다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F1.jpg

Fig. 1.

Flow rate diagram of pulse

3.2 수치모의 조건

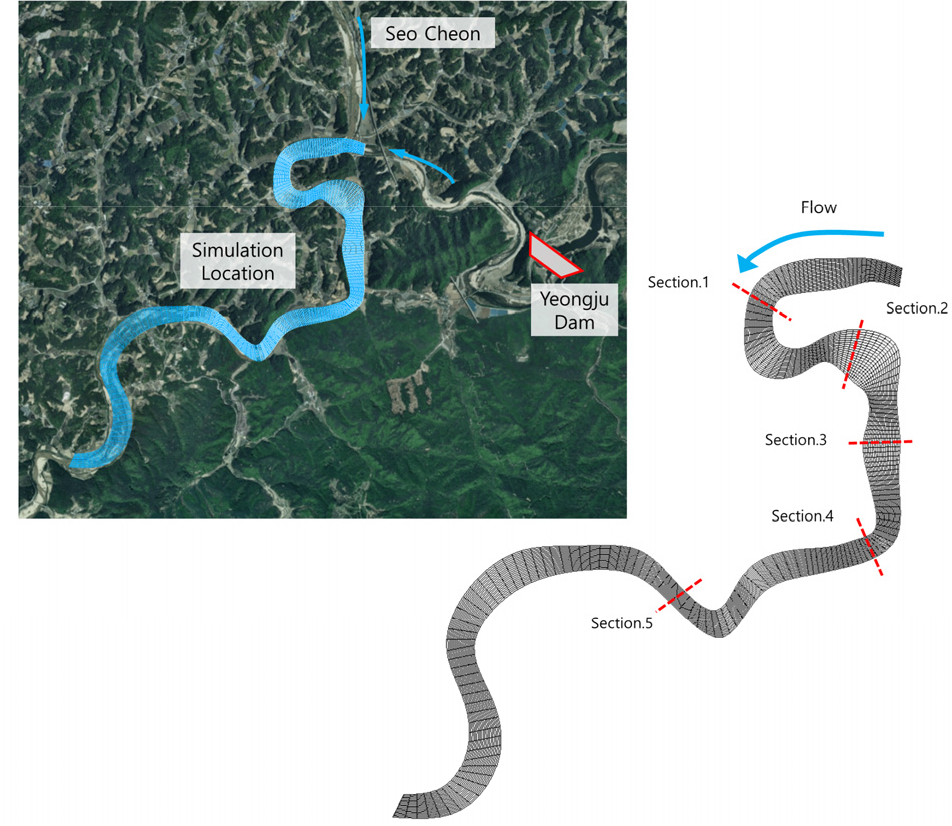
본 연구의 수치모의 대상지역은 영주댐 하류 하천이며, 경상북도 영주시 문수면 수도리를 포함하여 서천 합류부 하류 지점이다. 영주댐은 2016년 12월에 준공하였으며, 댐의 길이 400 m, 높이 55.5 m로 콘크리트 표면 착수벽형 석괴댐이다. 영주댐의 유역면적은 500 km², 총 저수용량은 181.1×106 m³, 유효저수용량은 160.4×106 m³이다. 내성천의 유로연장 은 108.20 km, 유역면적 1,814.71 km²인 하천이다. 영주댐이 준공된 이후 댐 하류하천에서는 유사이송과 유량이 감소하여 하천 육역화가 진행되어 하천환경 및 생태적으로 문제가 발생하고 있다(Lee and Kim, 2021). 이에 본 연구에서는 영주댐의 방류량과 패턴의 변화에 따른 댐 하류하천에서 사주의 발달과 지형변화 과정을 모의하여 개선 방안을 제시하고자 한다.

연구범위는 영주댐 하류 내성천에서 서천이 합류하는 지점부터 하류로 8.402 km (No.16.693~25.549)이며, 하상경사는 0.0014 이다. 하상토의 평균입경은 1.05 mm이며, Manning의 조도계수는 하천의 수위 등 수리량 변화 및 하상변화 정도에 영향을 미치기 때문에 중요한 요소이다. 정확도가 높은 조도계수를 얻기 위해서는 하상재료조사 등 현장조사를 통해 적합한 조도계수를 구하는 것이 원칙이다(KWRA, 2009). 따라서, MOLIT (2012)에서 내성천 하류권부터 영주댐 직상류까지 현장조사를 통해 하상재료 구성물질 및 하상상태를 고려하여 제시한 0.031을 적용하였다.

수치모의 시간은 강우시간을 고려하여 72 hrs로 설정하였다. 수치모의 계산 시간 간격은 0.01 sec로 설정하였다. 계산 격자 설정은 흐름방향으로 평균 71 m, 흐름의 횡방향으로 평균 9.6 m로 하였으며, 격자의 종방향과 횡방향의 비는 7.30:1 이다.

본 수치모의에 적용되는 유량을 산출하기 위해 내성천에 위치한 석탑교 수위표(No. 19.044)에서 관측한 2010년부터 2018년까지의 시단위 유량자료를 사용해 해당 유역에 해당되는 유량의 정규화(Normalizing)을 실시하였다. 석탑교 수위표에서 2010년부터 2018년까지 관측한 홍수량의 편차가 크기 때문에 정규화를 하여 모든 자료가 같은 정도의 스케일로 반영될 수 있도록 특성값을 조정하였다. 여기서 유량 정규화는 다음과 같이 실시하였다. 1) 연도별 최대첨두유량을 가지는 홍수의 수문곡선을 추출한다. 2) 각 홍수의 첨두유량으로 수문곡선 값을 나누어 최대값이 ‘1’이 되도록 한다. 3) 첨두유량이 ‘1’이된 각 수문곡선 그래프를 ‘1’값을 기준으로 중첩시킨다. 4) 중첩된 수문곡선을 시간별 평균한다. 5) 시간별 평균된 수문곡선에 적용하고자 하는 첨두유량을 곱하여 정규화된 수문곡선을 구축한다 (Baek, 2020).

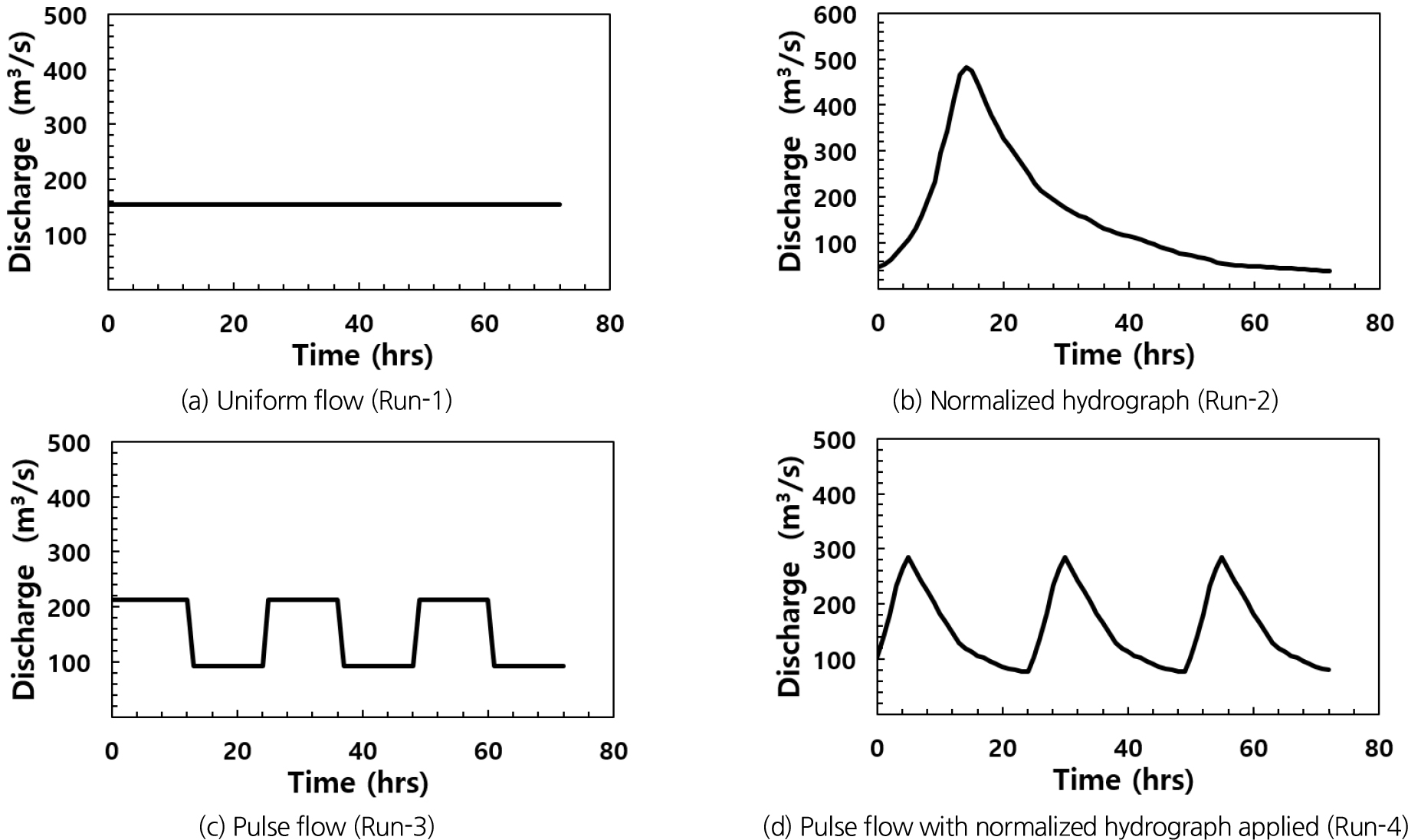
수치모의에 적용되는 유량의 형태는 4개의 유형이며, 첫 번째는 등류(Run-1), 두 번째는 정규화된 단일홍수(Run-2), 세 번째는 펄스방류(Run-3), 네 번째는 정규화된 펄스방류(Run-4)이다. 수치모의 시간은 72 hrs로 동일하게 적용하였다.

등류(Run-1)의 지속유량은 정규화된 단일홍수(Run-2)에서 시간별 유량값을 평균한 값으로 153.6 m³/s 이다. 정규화된 단일홍수(Run-2)는 내성천 석탑교 수위표에서 2012년 09월 17일 21시에 발생한 첨두유량(483.0 m³/s)을 정규화된 수문곡선에 곱하여 적용하였다. 펄스방류(Run-3)은 한 주기에 등류(Run-1) 적용값인 153.6 m³/s가 평균이 되도록 최대 펄스유량이 213.0 m³/s이고, 최소 펄스유량은 92.7 m³/s으로 적용해서 세 번의 주기로 설정하였다. 정규화된 펄스방류(Run-4)는 정규화된 수문곡선에 펄스패턴을 적용하였다. Fig. 2는 본 수치모의에 적용되는 유량곡선이며, 수치모의를 위한 유량 조건은 Table 1에서 제시되었다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F2.jpg

Fig. 2.

Discharge hydrograph for numerical modeling conditions

Table 1.

Flow conditions for numerical simulations

Cases	Time (hrs)	$Q_{\max}$ (m³/s)	$Q_{\min}$ (m³/s)	Note
Run-1	72	153.6	153.6	Uniform flow / Fig. 2(a)
Run-2	72	483.0	80.6	Normalized hydrograph / Fig. 2(b)
Run-3	72	213.0	92.7	Pulse flow / Fig. 2(c)
Run-4	72	285.2	100.6	Pulse flow with normalized hydrograph applied / Fig. 2(d)

MOLIT (2012)는 영주댐 홍수조절방식을 일정량 조절방식으로 재현기간 200년 빈도로 홍수량(2,600 m³/s)에 대한 첨두방류량(713 m³/s)을 60 hrs 동안 방류하는 세부 운영방식을 제시하고 있다. 그러나 본 연구에서는 댐 운영의 용이성을 고려하여 펄스 방류의 주기(1 cycle)을 24 hrs으로 설정하고, 이를 3회 반복되도록 72 hrs로 설정하였다(Figs. 2(c) and 2(d)).

3.3 수치모의 검증

2차원 수치모형의 부정류에 대한 적용성을 검토하기 위하여 석탑교 수위표 관측값, Nays2DH 모형 수치모의 결과와 신뢰성을 높이기 위해 실무에서 사용되고 있는 1차원 모형인 HEC-RAS의 수치모의 결과와 비교하였다. 석탑교 수위표 관측값과 수치모의 결과값을 비교하기 위해 석탑교 수위표(모의구간 하류로부터 2.351 km지점)를 중심으로 8.856 km 구간의 지형을 구축하였으며, 관측값의 홍수위는 2011년 05월 10일 11시부터 2011년 05월 15일 03시까지 관측결과이다.

관측값과 수치모의 결과를 비교 검증하기 위한 지표로 AER (Average Error Rate), MAE (Mean Absolute Error), NSE (Nash-Sutcliffe Efficiency)와 RMSE (Root Mean Square Error)를 활용하였다. AER은 평균 오차율이고, MAE는 평균절대오차를 나타내며 관측값과 수치모의 결과값의 절대값 오차를 평균한 값이다. NSE는 Nash-Sucliffe 효율로 수치모의 결과의 정확성을 검증하는 지표이며, 지표값이 ‘1’에 가까울수록 관측값과 수치모의 결과값이 일치하는 것을 의미한다(Gupta and Kling, 2011). RMSE는 평균제곱근오차로 오차의 제곱을 산술 평균값의 제곱근으로 불일치도를 나타내는 지표이며, 지표값이 ‘0’에 가까울수록 일치하는 것을 의미한다(Chai and Draxler, 2014). AER, MAE, NSE, RMSE의 산정식은 각각 Eqs.(12a)~(12d)와 같다.

(12a)

A E R = |\frac{H_{o} - H_{m}}{H_{m}}| \times 100

(12b)

M E A = \frac{\sum |H_{o} - H_{m}|}{n}

(12c)

N S E = 1 - \frac{\sum {(H_{o} - H_{m})}^{2}}{\sum {(H_{o} - \bar{H})}^{2}}

(12d)

R M S E = \sqrt{\frac{\sum (H_{o} - H_{m})^{2}}{n}}

여기서, $H_{o}$ 는 관측값, $H_{m}$ 는 수치모의 결과값, $\bar{H}$ 는 관측값의 평균이다.

3.3.1 관측값과 Nays2DH 수치모의 결과 비교

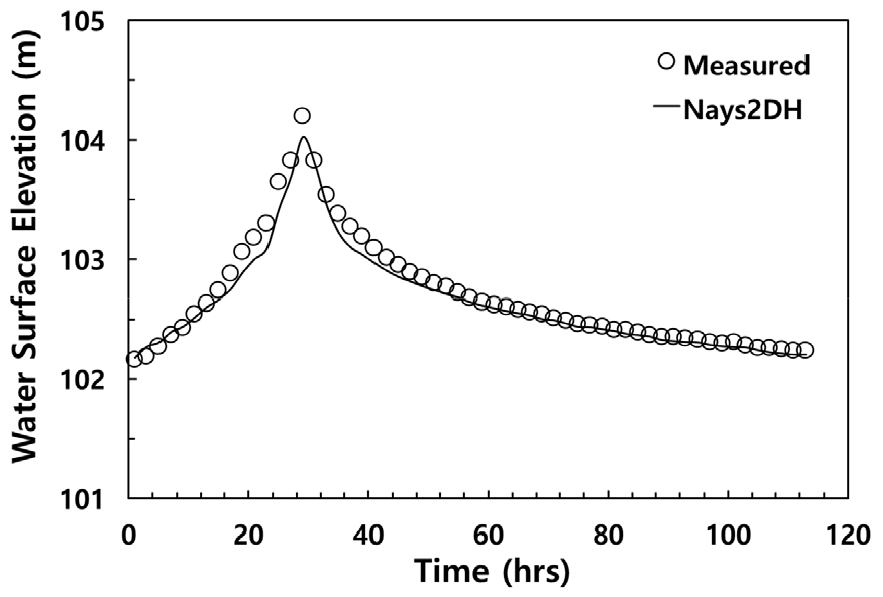
대상구간의 시간대별 수위 관측값과 Nays2DH 의 수위 모의결과를 비교하였다. 수위 관측값은 내성천 석탑교의 수위표 자료를 사용하였다. AER은 0.055%, MAE는 0.059 m, NSE는 0.967, RMSE는 0.060 m로 계산되었다. NSE 값이 1에 근접하고, RMSE도 0에 근접하는 것을 확인하였다(Table 2). Fig. 3는 석탑교 수위표에서 수위에 대한 관측값과 계산값이 잘 일치함을 보여주고 있다.

Table 2.

Mean verification index (Observed value-Nays2DH)

	AER (%)	MAE (m)	NSE	RMSE (m)
Mean	0.055	0.056	0.967	0.060

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F3.jpg

Fig. 3.

Result of unsteady simulation (Observed value - Nays2DH)

3.3.2 Nays2DH와 HEC-RAS 수치모의 결과 비교

1차원 모형인 HEC-RAS와 2차원 모형인 Nays2DH의 종방향 평균 수위를 비교하였다. Fig. 4은 1차원 수치모형 HEC- RAS와 2차원 수치모형 Nays2DH의 수위에 대한 모의결과를 나타낸다. AER은 0.058%, MAE는 0.067 m, NSE는 0.999, RMSE는 0.095 m로 계산되었다(Table 3). NSE 값이 1에 근접하는 것을 볼 수 있으며, RMSE도 0에 근접하여 수치모의 결과가 잘 일치하는 것을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F4.jpg

Fig. 4.

Result of unsteady simulation (HEC-RAS - Nays2DH)

Table 3.

Mean verification index (HEC-RAS-Nays2DH)

	AER (%)	MAE (m)	NSE	RMSE (m)
Mean	0.055	0.056	0.967	0.060

Kang et al. (2016)은 영주댐을 중심으로 ‘댐 하류하천에서 유사공급에 의한 하도의 지형변화 수치모의 분석’를 수행하였다. Nays2DH 모형의 유사공급에 의한 하상 및 지형변동 수치모의 적용성을 검토하기 위하여 Cui et al. (2003)의 실내실험 결과를 이용하였다. Cui et al. (2003)은 유사가 하도에 불연속적인 더미(맥동) 형식으로 공급되었을 때, 이송과 확산 과정을 거치면서, 하류로 이동하는 현상을 실내실험을 통하여 파악하였다. 수치모의 결과는 실내실험에서 보여준 토사더미의 이송과 확산과정을 잘 모의하였고, 실내실험에서 제시된 결과와 잘 일치하였다. 더욱이 실험 초기에 토사더미 상류에서는 수면이 불연속적으로 튀는 도수(hydraulic jump)가 발생하지만, 토사더미 하류에서는 완만하게 감소하는 수면형이 발생하는 현상까지도 파악할 수 있었다. 따라서 본 연구에서 내성천에서 하상변동에 대한 수치모형의 적용성 검토 내용은 Kang et al. (2016)에서 자세히 기술되어있다.

4. 수치모의 결과

수치모의 결과 분석은 모의구간에서 특정 지점을 선정하여 모의별 비교분석을 하였다. 분석 지점은 수치모의 시 다양한 지형에서의 하천 지형변화를 분석하기 위해 만곡부 지점 Section 1, Section 2, Section 4와 만곡부 이후 직선하도 지점 Section 3, Section 5로 선정하였다(Fig. 5).

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F5.jpg

Fig. 5.

Analysis point

4.1 유량패턴에 따른 지형변화 분석

Fig. 6는 수치모의 조건에 따른 횡단면의 평균 하상변동량을 종방향을 보여주고 있다. 이 그림에서, 유량조건에 따른 주요 분석지점(Section)과 모의구간에서의 종방향 하상변동량에 대한 특성을 비교할 수 있다. 첫 번째로 Run-1(등류)과 Run-2(단일홍수)를 비교하면 총 하상변동량이 각각 29.88 m, 27.46 m로 전체적으로 변동량과 퇴적 및 침식의 범위는 Run-1(등류)에서 큰 것을 확인할 수 있다. 두 번째로 Run-3(펄스방류)와 Run-4(정규화된 펄스방류)를 비교하면, 총 하상변동량이 각각 29.63 m, 31.87 m로 Run-4(정규화된 펄스방류)가 큰 것을 볼 수 있다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F6.jpg

Fig. 6.

Elevation change in longitudinal section by simulation

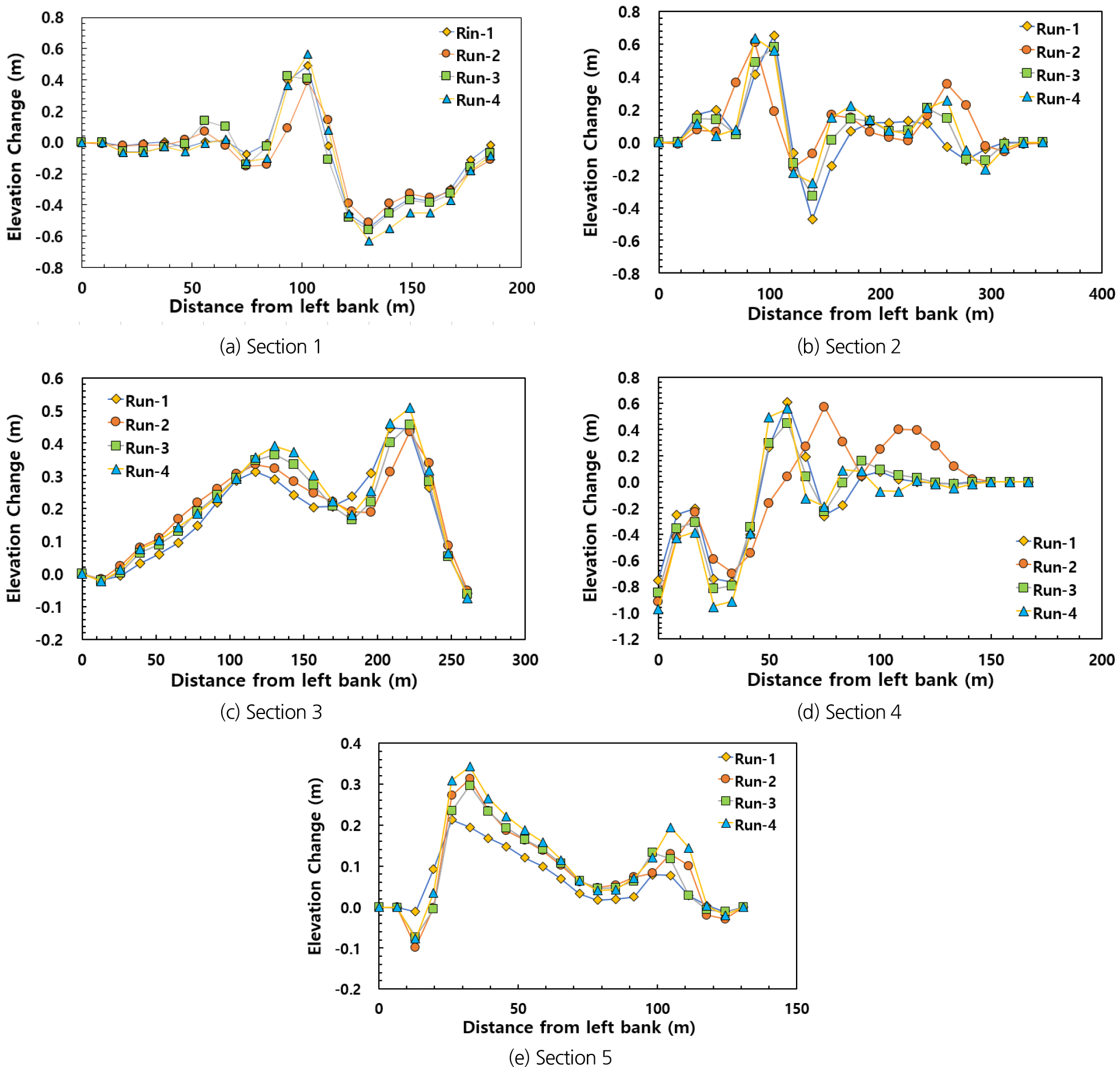
Fig. 7은 분석지점별 수치모의 조건에 대한 횡단면 하상변동량을 보여주고 있다. Section 1은 모의구간 상류지점이기 때문에 수치모의 조건에 따른 하상 지형변화 패턴이 비슷하게 나타났다(Fig. 7(a)). 여기서 Run-4가 최대 퇴적 높이 0.56 m, 최대 침식 깊이 -0.63 m로 변화폭이 가장 컸다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F7.jpg

Fig. 7.

Comparative analysis by simulation

Section 2의 경우에는 Run-1 조건에서 최대 퇴적 높이 0.65 m, 최대 침식 깊이가 -0.47 m로 변화폭(1.12 m)이 가장 큰 것으로 나타났다. 최대 퇴적 높이는 Run-4가 2.53 m로 가장 높게 나타났으며, 최대 침식 깊이는 Run-1이 -0.86 m로 가장 크게 나타났다(Fig. 7(b)). Section. 3은 직선구간으로 지형변화 패턴이 일정하며 주로 퇴적이 진행되었다. 최대 퇴적높이는 4.57 m로 Run-4 이 가장 크며, Run-1이 3.93 m로 가장 작았다(Fig. 7(c)).

Section. 4에서는 우안에서 Run-2 조건일 때의 퇴적량이 두드러지게 많은 것을 보여준다. 이러한 이유는 직선하도 구간이 끝나고 하도가 좌측으로 만곡되면서 첨두유량일때 만곡부 내측인 우안에 쌓인 유사가 유량이 작아지면서 하류로 쓸려 내려가지 못한 것으로 판단된다. 이때, 최대 퇴적 높이는 2.72 m이었다. 동일한 지점에서 Run-1과 Run-3에서는 퇴적량이 미미했으며, Run-4의 경우에는 -0.95 m로 침식되는 것으로 나타났다(Fig. 7(d)).

Section 5에서는 Run-1이 퇴적높이가 1.41 m로 가장 작았으며, Run-4의 퇴적높이가 최대 0.34 m로 가장 높았다. 특히, 우안으로부터 120 m 지점에서는 Run-1을 제외한 다른 모의조건에서는 세굴이 되었다. 이것은 유량 패턴 변화의 영향이 하류로 길게 이어진다는 것을 보여준다(Fig. 7(e)).

Table 4는 구간별 퇴적량과 침식량의 절대값을 더한 절대변동량을 비교한 결과이다. Section 1, 3에서는 Run-1, Run-2, Run-3, Run-4 순으로 Run-4에서 절대변화량이 가장 크지만, Section 4, 5에서는 Run-2의 절대변동량이 Run-1과 Run-3보다 큰 것을 확인하였다.

Table 4.

Total change by section (m)

Case	Section 1	Section 2	Section 3	Section 4	Section 5
Run-1	3.68	2.90	3.93	4.78	1.41
Run-2	3.70	2.80	4.20	6.28	2.11
Run-3	4.34	2.87	4.20	4.85	1.97
Run-4	4.65	3.23	4.57	5.81	2.41

4.2 하상기복지수 분석

유량패턴 변화에 따른 하상고의 변화를 정량적으로 파악하기 위해 각 단면의 하상기복지수(Bed Relief Index, BRI)를 분석 하였다. BRI는 횡단면의 하상고 자료를 이용하여 평균 하상고에 대한 각 단면의 표준편차를 나타내며, 다음 식으로 정의된다(Hoey and Sutherland, 1991; Jang, 2013).

(13)

B R I = \frac{(\sum_{i = 1}^{n - 1} {[(z_{i}^{2} + z_{i + 1}^{2}) / 2]}^{0.5} [x_{i + 1} - x_{i}])}{(x_{n} - x_{1})}

여기서, $x_{i + 1} - x_{i}$ 는 $i$ 과 $i + 1$ 사이의 종방향 거리이며, $x_{n} - x_{1}$ 는 하도 전체 길이이다. $z_{i}$ 는 $x_{i}$ 지점에서 하상고이다. BRI가 큰 것은 하상의 변화가 큰 것을 의미한다. Fig. 8은 모의구간에서 유량 패턴 변화에 의한 BRI를 분석한 결과이다. Run-1, Run-3, Run-4 조건의 경우 시간이 지남에 따라 BRI가 증가하였다. 특히, 정규화된 단일홍수(Run-2)의 경우에는 첨두유량(14 hrs) 이후 30 hrs 까지 BRI가 3.07로 급격하게 증가하면서 55 hrs에는 BRI가 최대 3.42로 가장 크게 나타났다. 그러나, 56 hrs부터는 BRI가 감소하여 수치모의가 끝날 때(72 hrs) BRI가 3.31로 펄스방류(Run-3) 조건과 비슷한 결과(3.34)를 보여주었다. 수치모의가 끝날 때 Run-1과 Run-4의 경우 BRI는 각각 2.95, 3.78로 나타났다. 따라서, 등류(Run-1)의 경우가 BRI가 가장 작게 나타났으며, 정규화된 펄스방류(Run-4)의 경우에는 일정하게 증가하면서 최종시간(72hr)에는 BRI가 가장 큰 것으로 나타났다. 따라서, 본 연구에서 확인하고자 하는 정규화된 펄스방류(Run-4) 조건이 하상고의 변화가 가장 크게 나타났다. 즉, 정규화된 펄스방류 조건일 때 시간이 지날수록 단일홍수와 등류보다 댐 하류하천에 역동적인 효과를 줄 수 있고, 역동성이 커지면서 환경개선에 효과를 가져올 수 있을 것이다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-12/N0200561204/images/kwra_56_12_04_F8.jpg

Fig. 8.

Bed Relief Index (BRI) due to flow change

5. 결 론

본 연구에서는 영주댐 하류 하천을 대상으로 2차원 수치모형인 Nays2DH를 적용하여 펄스방류 등 다양한 유량패턴을 적용하면서 하류 하천의 역동성을 파악하기 위해 하도의 지형변화 특성을 분석하였다. 또한, 댐 하류 하천의 인위적인 교란을 저감하고 하도의 역동성을 증가시키기 위한 하류 하천 관리방안을 제시하기 위해 하상기복지수 분석을 실시하였으며, 그 결과를 요약하면 다음과 같다.

1) 2차원 수치모형인 Nays2DH의 적용성 검토를 위해 영주댐 하류 석탑교 수위표의 수위 관측값과 1차원 수치모형인 HEC-RAS의 결과와 비교하고, HEC-RAS의 종방향 평균수위 모의결과와 Nays2DH의 모의결과를 비교하였으며, Nays2DH 모의결과가 잘 일치하는 것을 확인할 수 있었다.

2) 같은 총 유량을 등류로 적용하였을 때(Run-1)와 유량정규화를 적용하였을 때(Run-2)의 수치모의 결과를 비교하면 모의구간 상류에서는 등류 일 때의 하상고의 변화가 소폭 증가하였으나, 하류에서는 유량정규화를 적용하였을 때 침식과 퇴적에 의해 변화가 증가하면서 하상고 변화량 또한 증가하였다.

3) 댐 운영 시 방류패턴의 변화로 댐 하류 하천에 역동적인 효과 분석을 위해 등류(Run-1), 펄스방류(Run-3), 정규화된 펄스방류(Run-4)로 비교하였다. 정규화를 적용한 펄스방류 조건일 때 하상고의 변동량과 변동 폭이 가장 큰 것으로 나타났다. 모의조건별 총 하상변화량은 Run-1은 29.88 m, Run-2는 27.46 m, Run-3은 29.63m 그리고 Run-4에서 31.87 m로 Run-4에서 가장 컸으며, Run-4에서 세굴과 퇴적의 변동폭이 가장 크게 나타났다.

4) 상류와 하류구간의 하상변화의 차이 정도를 파악하기 위하여 BRI를 분석한 결과, Run-1, Run-3, Run-4 조건의 경우 시간이 지남에 따라 BRI가 일정하게 증가하였다. 그러나, Run-2의 경우 첨두유량(14 hrs) 이후 30 hrs 까지 BRI가 급격하게 증하지만 점점 증가폭이 감소하면서 56 hrs부터는 감소하였다. 수치모의가 끝날 때(72 hrs) BRI는 Run-1에서는 2.95, Run-2에서는 3.31, Run-3에서는 3.34, Run-4에서는 3.78이다. 따라서, 정규화된 펄스방류(Run-4) 조건이 하상고의 변화가 가장 크게 나타났다. 즉, 정규화된 펄스방류 조건일 때 시간이 지날수록 단일홍수와 등류보다 댐 하류하천에 역동적인 효과를 줄 수 있고, 역동성이 커지면서 환경개선에 효과를 가져올 수 있다.

Acknowledgements

본 결과물은 환경부의 재원으로 한국환경산업기술원의 가뭄대응관리 혁신기술개발사업의 지원을 받아 연구되었습니다(2022003610004).

Conflicts of Interest

The authors declare no conflict of interest.

References

Ashida, K., and Michiue, M. (1972). "Study on hydraulic resistance and bed-load transport rate in alluvial streams." Transactions, Japan Society of Civil Engineering, JSCE, Vol. 1972, No. 206, pp. 59-64.

Baek, T.H. (2020). Numerical analysis of effect of flow pluses on geomorphic changes downstream of dam. Master Thesis, Korea National University of Transportation.

Brandt, S.A. (2000). "Classification of geomorphological effects downstream of dams." Catena, Vol. 40, No. 4, pp. 375-401. 10.1016/S0341-8162(00)00093-X

Bunte, K. (2004). Gravel mitigation and augmentation below hydroelectric dams: A geomorphological perspective. Report to the Stream Systems Technology Center, USDA, Forest Service, Rocky Mountain Research Station, Fort Collins, CO, U.S.

Chai, T., and Draxler, R.R. (2014). "Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature." Geoscientific Model Development, Vol. 7, No. 3, pp. 1247-1250. 10.5194/gmd-7-1247-2014

Cui, Y., Parker, G., Lisle, T.E., Gott, J., Hansler-Ball, M.E., Pizzuto, J.E., Allmendinger, N., and Reed, J.M. (2003). "Sediment pulses in mountain rivers: 1. experiments." Water Resources Research, Vol. 39, No. 9. 1239. doi: 10.1029/2002WR001803. 10.1029/2002WR001803

Engelund, F. (1974). "Bed Characteristics in alluvial channel bends." Journal of the Hydraulics Division, ASCE, Vol. 100, No. 11, pp. 1631-1648. 10.1061/JYCEAJ.0004109

Galay, V.J. (1983). "Causes of river bed degradation." Water Resouroes Research, Vol. 19, No. 5, pp. 1057-1090. 10.1029/WR019i005p01057

Gupta, H.V., and Kling, H. (2011). "On typical range, sensitivity, and normalization of Mean Squared Error and Nash-Sutcliffe Efficiency type metrics." Water Resources Research, Vol. 47, No. 10, W10601. doi: 10.1029/2011WR010962. 10.1029/2011WR010962

Hoey, T.B., and Sutherland, A.J. (1991). "Channel morphology and bedload pulses in braided rivers: A laboratory study." Earth Surface Processes and Landforms, Vol. 16, pp. 447-462. 10.1002/esp.3290160506

Jang, C.-L. (2013). "Experimental analysis of the morphological changes of the vegetated channels." Journal of Korea Water Resources Association, KWRA, Vol. 46, No. 9, pp. 909-919. 10.3741/JKWRA.2013.46.9.909

Jang, C-L., and Shimizu, Y. (2010). "Numerical simulation of sand bars downstream of Andong Dam." Journal of Civil and Environmental Engineering Research, KSCE, Vol. 30, No. 4B, pp. 379-388.

Jang, C-L., and Woo, H.S. (2009). "Analysis of bed material changes by flushing flow from Daecheong Dam." Journal of Korea Water Resources Association, KWRA, Vol. 42, No. 10, pp. 845-855. 10.3741/JKWRA.2009.42.10.845

Kang, K.-H., Jang, C.-L., Lee, G.H., and Jung, K. (2016). "Numerica zl analysis of the morphological changes by sediment supply at the downstream channel of Youngju Dam." Journal of Korea Water Resources Association, KWRA, Vol. 49, No. 8, pp. 693-705. doi: 10.3741/JKWRA.2016.49.8.693 10.3741/JKWRA.2016.49.8.693

Kondolf, G.M. (1997). "Hungry water: Effects of dams and gravel mining on river channels." Environmental Management, Vol. 21, No. 4, pp. 533-552.

Korea Water Resources Association (KWRA) (2009). River design standard commentary.

Lee, T.H., and Kim, S.H. (2021). "Analysis of changes in cross section and flow rate due to vegetation establishment in Naeseong Stream." Journal of Korea Water Resources Association, KWRA, Vol. 54, No. 3, pp. 203-215. 10.3741/JKWRA.2021.54.3.203

Ministry of Landm Infrastructure and Transport (MOLIT) (2012). Basic river plan for the midstream area of Naeseongcheon Stream.

National Water Commission (NWC) (2009). Pulsed flows: A riview of environmental costs and benefits and best practice. Canberra, Australia.

Page, K., Read, A., Frazier, P., and Mount, N. (2005). "The effect of altered flow regime on the frequency and duration of bankfull discharge: Murrumbidgee River, Australia." River Research and Applications, Vol. 21, No. 5, pp. 567-578. 10.1002/rra.828

Pitlick, J., and Wilcock, P. (2001). "Relations between streamflow, sediment transport, and aquatic habitat in regulated rivers." Geomorphic Processes and Riverine Habitat, Vol. 4, pp. 185-198.

Shin, Y.H., and Julien, P.Y. (2011). "Effect of flow pulses on degradation downstream of Hapcheon Dam, South Korea." Journal of Hydraulic Engineering, ASCE, Vol. 137, No. 1, pp. 100-111. 10.1061/(ASCE)HY.1943-7900.0000287

Watanabe, A., Fukuoka, S., Yasutake, Y., and Kawaguchi, H. (2001). "Method for arranging vegetation griffons at bends for control of bed variation." Collection of Papers on River Engineering, Vol. 7, pp. 285-290.

Williams, G.P., and Wolman, M.G. (1984). Downstream effects of dams on Alluvial Rivers. United States Geological Survey Professional Paper, 1286, U.S. Government Printing Office Washington, D.C., U.S. 10.3133/pp1286

Journal of Korea Water Resources AssociationISSN:2799-8746(Print) 2799-8754(Online)한국수자원학회

Preview

Numerical analysis of geomorphic changes in rivers due to dam pulse discharge of Yeongju Dam

ABSTRACT

MAIN

(1)

(2a)

(2b)

(3a)

(3b)

(4a)

(4b)

(5)

(6)

(7a)

(7b)

(8)

(9)

(10)

(11)

Fig. 1.

Flow rate diagram of pulse

Fig. 2.

Discharge hydrograph for numerical modeling conditions

Table 1.

Flow conditions for numerical simulations

(12a)

(12b)

(12c)

(12d)

Table 2.

Mean verification index (Observed value-Nays2DH)

Fig. 3.

Result of unsteady simulation (Observed value - Nays2DH)

Fig. 4.

Result of unsteady simulation (HEC-RAS - Nays2DH)

Table 3.

Mean verification index (HEC-RAS-Nays2DH)

Fig. 5.

Analysis point

Fig. 6.

Elevation change in longitudinal section by simulation

Fig. 7.

Comparative analysis by simulation

Table 4.

Total change by section (m)

(13)

Fig. 8.

Bed Relief Index (BRI) due to flow change

Acknowledgements

Conflicts of Interest

References