Application of sequence to sequence learning based LSTM model (LSTM-s2s) for forecasting dam inflow

Heechan Han; Changhyun Choi; Jaewon Jung; Hung Soo Kim

doi:10.3741/JKWRA.2021.54.3.157

Preview

Research Article

Journal of Korea Water Resources Association. 31 March 2021. 157-166
https://doi.org/10.3741/JKWRA.2021.54.3.157

Application of sequence to sequence learning based LSTM model (LSTM-s2s) for forecasting dam inflow

Sequence to Sequence based LSTM (LSTM-s2s)모형을 이용한 댐유입량 예측에 대한 연구

Heechan Han^a

Changhyun Choi^b

Jaewon Jung^c

Hung Soo Kim^d

한 희찬^a

최 창현^b

정 재원^c

김 형수^d

^aPh.D Candidate, Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, USA

^bAssistant manager, Risk Management Office, KB Claims Survey and Adjusting, Seoul, Korea

^cSenior Researcher, Institute of Water Resources System, Inha University, Incheon, Korea

^dProfessor, Department of Civil Engineering, Inha University, Incheon, Korea

^a콜로라도 주립 대학교 토목환경공학과 박사과정

^bKB손해사정 위험관리실 대리

^c인하대학교 수자원시스템연구소 선임연구원

^d인하대학교 사회인프라공학과 교수

^{*Corresponding Author}

ABSTRACT

Forecasting dam inflow based on high reliability is required for efficient dam operation. In this study, deep learning technique, which is one of the data-driven methods and has been used in many fields of research, was manipulated to predict the dam inflow. The Long Short-Term Memory deep learning with Sequence-to-Sequence model (LSTM-s2s), which provides high performance in predicting time-series data, was applied for forecasting inflow of Soyang River dam. Various statistical metrics or evaluation indicators, including correlation coefficient (CC), Nash-Sutcliffe efficiency coefficient (NSE), percent bias (PBIAS), and error in peak value (PE), were used to evaluate the predictive performance of the model. The result of this study presented that the LSTM-s2s model showed high accuracy in the prediction of dam inflow and also provided good performance for runoff event based runoff prediction. It was found that the deep learning based approach could be used for efficient dam operation for water resource management during wet and dry seasons.

Keywords

Dam inflow forecasting

Deep learning

LSTM with Sequence-to-Sequence learning

효율적인 댐 운영을 위해서는 높은 신뢰도를 기반으로 하는 유입량 예측이 요구된다. 본 연구에서는 최근 다양한 분야에서 사용되고 있는 데이터 기반의 예측 방법 중 하나인 딥러닝을 댐 유입량 예측에 활용하였다. 그 중 시계열 자료 예측에 높은 성능을 보이는 Sequence-to-Sequence 구조 기반의 Long Short-Term Memory 딥러닝 모형(LSTM-s2s)을 이용하여 소양강 댐의 유입량을 예측하였다. 모형의 예측 성능을 평가하기 위해 상관계수, Nash–Sutcliffe 효율계수, 평균편차비율, 그리고 첨두값 오차를 이용하였다. 그 결과, LSTM-s2s 모형은 댐 유입량 예측에 대한 높은 정확도를 보였으며, 단일 유량 수문곡선 기반의 예측 성능에서도 높은 신뢰도를 보였다. 이를 통해 홍수기와 이수기에 수자원 관리를 위한 효율적인 댐 운영에 딥러닝 모형의 적용 가능성을 확인할 수 있었다.

키워드

댐 유입량 예측

딥러닝

LSTM with Sequence-to-Sequence learning

MAIN

1. 서 론
2. 자료 및 연구방법
2.1 대상지역 및 자료 수집
2.2 LSTM-s2s 모형
2.3 입력자료 구축
2.4 평가 지표
3. 모형 적용 및 분석
3.1 유입량 예측을 위한 LSTM-s2s 모형의 최적화
3.2 LSTM-s2s 모형을 활용한 댐 유입량 예측
4. 요약 및 결론

1. 서 론

정확한 유량 예측은 홍수 방지, 가뭄 완화, 저수지 운영, 생태계 보존 등의 수자원 관리에 매우 중요하다(Zhang et al., 2012; Chen et al., 2016; Blöschl et al., 2019; Palmer and Ruhi, 2019). 현재 국내에는 수자원 관리를 위해 21개의 다목적댐과 14개의 용수댐, 약 17,000개 이상의 농업용 저수지를 포함한 많은 댐이 건설되어 운영되고 있으며, 댐 상류로부터의 유입량과 현재 저수량을 고려하여 하류의 방류량을 결정하는 것은 안전하고 효율적인 댐의 운영을 위해 필수적이다(Mok et al., 2020). 이를 위해서는 상류로부터 들어오는 유입량에 대한 보다 정확한 예측이 요구된다.

일반적으로 유량 예측을 위해 물리적 모형(Physically based models)과 경험적 모형(Empirical models) 등의 다양한 수문 모형을 이용하는데, 연구 초창기에는 수문 시스템을 단순화한 물리적 모형을 이용한 연구들이 주를 이루었다(Bicknell et al., 1996; Kim et al., 2007; Neitsch et al., 2011; Kang et al., 2013; Devia et al., 2015; Noh et al., 2016). 그러나 물리적 모형은 복잡한 수문 시스템을 단순화하는 과정에서 기상학적, 지형학적, 지질학적 다양한 변수를 모두 고려하기가 어려운 한계가 있으며, 이러한 불확실성으로 인해 계산과정을 거치는 동안 오차가 누적되는 단점이 있다(Jung et al., 2018).

데이터 기반의 경험적 모형은 통계적 관점에서 입력-출력 관계를 추정하는 모형으로 연구 초기에는 autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA)와 같은 선형 모형을 통해 유량을 예측하였지만, 현실의 비선형적인 요소들을 선형 모형으로 해석하기 어려운 부분들이 있어 유연성이 떨어지는 모습을 보였다(Montanari et al., 1997; Kim, 2010). 머신러닝(Machine learning)의 발전과 함께 이러한 문제를 해결해 줄 수 있는 비선형 모형이 유량 예측에 사용되었는데, artificial neural network (ANN), support vector machine (SVM), random forest (RF), extreme gradient boosting (XGBoost), adaptive neuro fuzzy inference system (ANFIS) 등 다양한 모형들을 통한 시도들이 있었다(Riad et al., 2004; Abrahart et al., 2004; Ghumman et al., 2011; Granata et al., 2016; Mosavi et al., 2018; Yan et al., 2018; Bae et al., 2019). 최근에는 머신러닝 기법 중 인간 두뇌 신경망 구조를 모방한 인공신경망에 바탕을 둔 딥러닝(Deep learning) 기반의 모형들이 기존 머신러닝 기반의 모형보다 높은 성능의 결과를 제공한다는 연구들이 등장하고 있으며(Chen et al., 2013; Shoaib et al., 2016; Assem et al., 2017; Park et al., 2018; Choi et al., 2020; Kim et al., 2020; Lee et al., 2020), 기존의 recurrent neural networks (RNN) 모형에 long short-term memory (LSTM)을 도입하면 예측 성능이 향상된다는 연구결과들이 보고되고 있다(Tian et al., 2018; Lee et al., 2018; Kratzert et al., 2018; Hu et al., 2018; Mok et al., 2020). Fan et al. (2020)은 LSTM 모형을 이용하여 강우-유출 모의를 수행하였고, 모의 성능을 확인하기 위해 대표적인 머신러닝 기법인 ANN과 Soil and Water Assessment Tool (SWAT)모형의 결과와 비교 및 분석하였다. 비교결과 LSTM 모형이 다른 모형에 비해 강우-유출 모의에 대한 높은 적용 가능성을 확인 할 수 있었다. 또한 Feng et al. (2020)은 유량 예측을 위해 LSTM 모형과 data-integration 기법을 함께 사용하였다. 또한 ANN 및 Sacramento Soil Moisture Accounting Model (SAC-SMA)모형과의 비교 및 분석을 수행하여 딥러닝 기법의 우수성을 확인하였다.

딥러닝 기반의 유량 예측모형을 통해 예측 정확도가 향상되었지만, 예측모형에 시계열 요소 간의 시간적 종속성은 여전히 고려되지 못하는 한계가 있다. 시간적 종속성은 서로 다른 시간 빈도에서 시계열 데이터의 변동 관련성을 반영하기 때문에, 시간적 종속성을 활용한다면 모형의 정확도는 향상될 여지가 있다. Cho et al. (2014a)와 Sutskever et al. (2014)는 LSTM에 시간적 종속성을 고려할 수 있는 Sequence-to-Sequence 구조를 이용한 모형(LSTM-s2s 모형)의 학습을 통해 향상된 언어번역 결과를 제시하였는데, 이러한 새로운 방법을 통해 연구자들은 언어번역 뿐만 아니라 음성인식, 게임, 데이터 분석, 지능형 시스템 및 기타 여러 분야에서 상당한 성능 개선을 이루었다. 그러나 지금까지 수문분야에서 LSTM-s2s 모형을 사용한 해외 연구는 매우 미비할 뿐만 아니라 국내의 연구 사례는 없다(Xu et al., 2019; Xiang et al., 2020). LSTM-s2s 모형을 이용한 해외의 수문분야 연구로는 Xiang et al. (2020)이 hourly 기반의 강우-유출 예측 모형을 개발하기 위해 LSTM-s2s 모형을 이용하여 최대 24시간 이후의 유량 예측을 수행하였다. 이 연구에서는 모형의 입력자료로 관측 강우, 유량, 그리고 증발산량 자료를 이용하였고, 다양한 평가 지표를 통해 LSTM-s2s 모형의 우수한 성능을 제시하였을뿐만 아니라 다른 모형들의 유량 예측 결과 비교를 통해 강우-유출 예측에 대한 LSTM-s2s 모형의 적용 가능성을 확인하였다.

대부분의 이전 연구들은 주로 시계열 요소 간 시간적 종속성을 고려하지 못하는 머신러닝과 LSTM 모형만을 사용하였다. 따라서 본 논문에서는 기존 연구들에서 사용한 모형에 비해 예측 성능이 우수할 것으로 판단되는 LSTM-s2s 모형을 강우-유출 모의에 활용하여 시간적 종속성을 고려한 LSTM-s2s 모형의 적용성을 검토하고자 한다. 이를 위해 국내의 대표적인 다목적댐인 소양감댐 유역을 대상으로 댐 유입량 예측을 위해 LSTM-s2s 모형을 활용한 유량예측 도구를 개발하였다. 2장에서는 연구 자료 및 방법에 대해 소개하고, 3장에서는 LSTM-s2s 모형의 구축 방법과 예측 성능을 검토하고, 4장에서는 연구결과에 대한 고찰을 제시하였다.

2. 자료 및 연구방법

2.1 대상지역 및 자료 수집

본 연구에서는 북한강의 상류에 위치한 소양강댐 유역을 대상지역으로 선정하였다. 소양강은 강원 중부지역을 지나 북한강에 합류하는 하천이며, 소양강의 총 유로연장은 166.2 km로 한강수계를 형성하는 남한강의 최대지류이다. 소양강댐은 북한강 유역의 유일한 다목적댐으로 춘천 북동쪽에 위치하고 있다(Bae et al., 2019). 소양강댐 유역의 유역면적은 2,694 km²이며, 유역평균표고 650 m, 유역평균경사가 46%이고 유역면적의 90% 이상이 산림으로 이루어져 있다(Han et al., 2017). 소양강댐 유역 인근 강우관측소로는 다음 Fig. 1에 제시된 것과 같이 인제, 홍천, 춘천 3개의 관측소가 위치한다.

본 연구에서 사용한 LSTM-s2s 모형의 입력 및 검증 자료는 국가수자원관리종합정보시스템(Water Resources Management Information System, WAMIS)에서 제공하는 2013년부터 2019년까지의 소양강댐에서 관측된 일 유입 유량과 지상강우관측 지점인 인제, 홍천 그리고 춘천에서 관측된 일 강우량 자료를 사용하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-03/N0200540302/images/kwra_54_03_02_F1.jpg

Fig. 1.

Study area of this study; Soyang River dam watershed

2.2 LSTM-s2s 모형

LSTM 모형은 시계열 데이터 처리를 위한 알고리즘인 RNN 모형을 기반으로 하고 있으며, RNN을 이용하여 장기간 데이터를 분석할 때 발생하는 gradient vanishing과 gradient exploding 문제를 해결하기 위해 Hochreiter and Schmidhuber (1997)에 의해 제안되었다. 수문 분야에서 LSTM 모형은 유량, 강우, 하천수위, 그리고 토양수분 등 다양한 수문학적 요소들의 분석과 예측을 위해 널리 사용되고 있다(Adeyemi et al., 2018; Hu et al., 2018; Zhang et al., 2018; Fan et al., 2020; Xiang et al., 2020).

LSTM 모형은 데이터의 특징에 따라 수많은 블록으로 구성되어 있으며, 각 블록은 세 개의 비선형 게이트인 입력(Input gate; i_t), 망각(Forget gate; f_t), 그리고 출력 게이트(Output gate; O_t)를 포함하고 있다. 모형에 입력된 입력 데이터는 게이트들을 통해 데이터가 포함하고 있는 정보를 얼마나 제거하고 유지할지 결정하게 된다. 망각게이트(f_t)에서는 이전 셀에서 들어온 데이터 정보를 얼마나 제거 및 유지할지 결정하는 역할을 한다. 입력게이트(i_t)에서는 새로운 데이터 정보 중 어떤 정보를 저장할지 결정하는 역할을 한다. 마지막으로, 출력게이트(O_t)에서는 셀에 저장된 정보 중 출력할 최종 결과물을 결정한다. 이러한 과정을 기반으로 LSTM 모형은 Eqs. (1) ~ (6)의 과정을 통해 구동된다.

(1)

f_{t} = σ (W_{f} ∙ [h_{t - 1}, x_{t}] + b_{f})

(2)

i_{t} = σ (W_{i} ∙ [h_{t - 1}, x_{t}] + b_{i})

(3)

O_{t} = σ (W_{o} ∙ [h_{t - 1}, x_{t}] + b_{o})

(4)

{\tilde{C}}_{t} = \tanh (W_{c} ∙ [h_{t - 1}, x_{t}] + b_{c})

(5)

C_{t} = f_{t} ∙ C_{t - 1} + i_{t} ∙ \tilde{C_{t}}

(6)

h_{t} = O_{t} ∙ \tanh (C_{t})

여기서, $σ$ = 활성화함수, $h_{t - 1}$ = 전 단계 출력값, W_f, W_i, W_o = 게이트 가중치, x_t = 입력값, b_c, b_f, b_i, b_o = 편향값, $\tilde{C_{t}}$ = 활성화함수를 통해 생성된 새로운 셀(cell) 상태, $C_{t - 1}$ = 이전 단계의 셀(cell) 상태, W_c = 셀 상태의 가중치, $h_{t}$ = 셀에서의 출력값이고 tanh = 활성화함수이다.

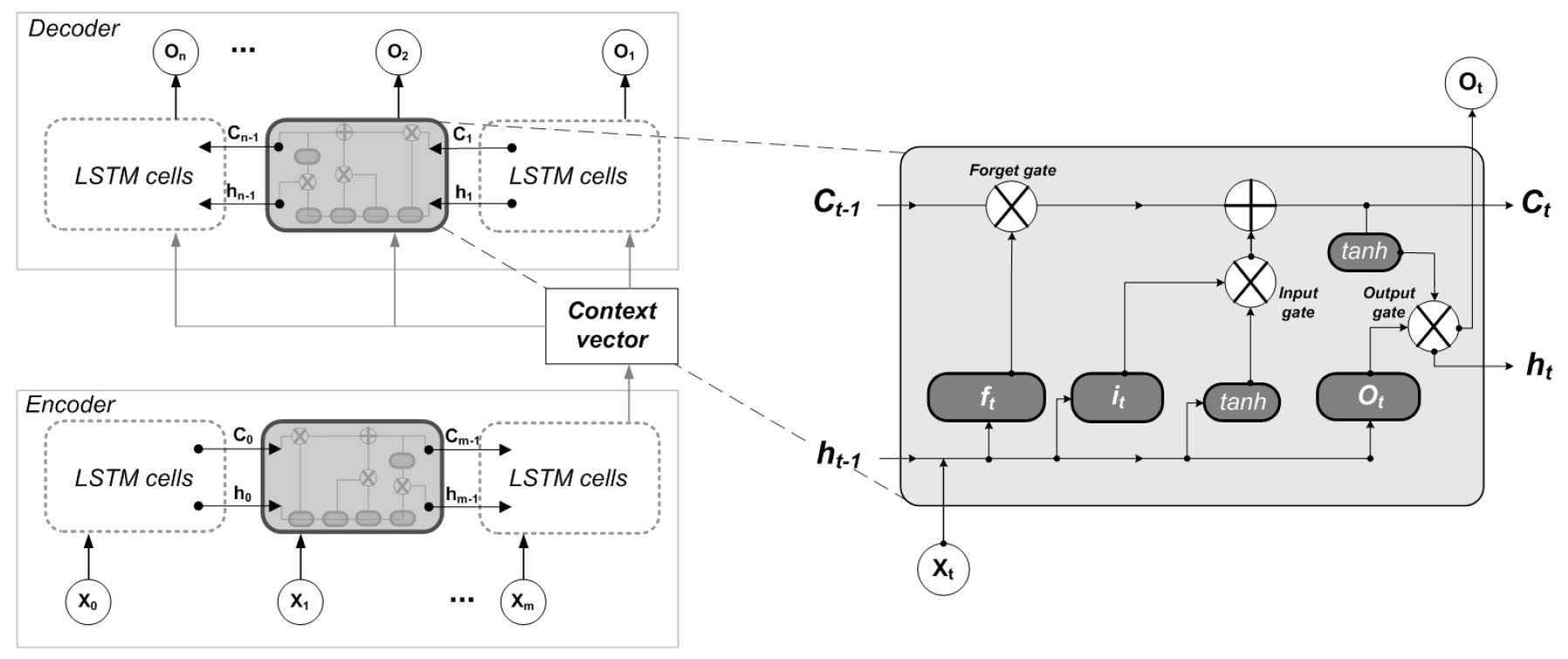
댐 유입량 예측을 위해 본 연구에서는 LSTM 기반의 LSTM-s2s 모형을 적용하였다. LSTM-s2s 모형은 Encoder-Decoder 모형이라고도 알려져 있으며 Cho et al. (2014b)에 의해 제안되었다. LSTM-s2s 모형은 출력값과 입력 자료 사이에 시간차가 존재할 경우 적용성이 높으며, 주로 언어번역, 이미지 인식과 같은 연속성을 기반으로 하는 자료의 분석을 위해 다양한 분야에서 사용되고 있다. 일반적으로 강우와 예측하고자 하는 유량의 경우, 두 변수 사이의 시간차가 분명하게 존재하기 때문에 본 연구에서는 기존의 LSTM 모형에서 발전된 LSTM-s2s 모형을 댐 유입량 예측에 적용하였다. LSTM-s2s 모형에 대한 추가적인 자세한 설명은 Cho et al. (2014a)와 Cho et al. (2014b)에서 확인 할 수 있다. Fig. 2는 LSTM 셀과 LSTM-s2s 모형의 개념도를 나타내고 있다(Xiang et al., 2020).

LSTM-s2s 모형은 기본적으로 LSTM 모형의 개념을 기반으로 하지만 LSTM-s2s 모형의 가장 큰 장점은 서로 다른 길이와 시간차를 가진 입력 자료와 출력값을 이용한다는 것이다. 본 연구에서 강우-유량 관계를 모의하기 위해 LSTM-s2s 모형에서 x_t는 관측 강우 자료를, context vector는 x_t로부터 필요한 정보를 수집하여 Decoder part의 초기 hidden state 역할을 한다. 그리고 O_t는 예측된 유량 값을 의미한다. 여기서, 입력 자료와 출력값의 시간적 길이를 나타내는 m과 n 값은 모형의 적용 목적에 따라 다르게 설정할 수 있다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-03/N0200540302/images/kwra_54_03_02_F2.jpg

Fig. 2.

Conceptual diagram of LSTM cells and LSTM-s2s model

2.3 입력자료 구축

본 연구에서는 LSTM-s2s 모형을 활용하여 소양강 댐의 일유입량을 예측하기 위해 과거에 관측된 일유입량과 주변 강우 관측소에서 관측된 일강우량 자료를 모형의 입력 자료로 사용하였다. 수집된 자료를 모형에 적용하기 전에 자료의 시간적 연속성을 강화시키기 위한 결측값의 보정이 필요하다. 특히, 자료의 시간적 연속성을 이용하는 LSTM 기반의 모형의 경우, 자료의 결측값을 보완하는 것은 필수적이다. 본 연구에서 사용한 유량 및 강우량의 관측이 이루어지지 않은 경우, 그 값을 전후 1일 관측자료의 평균치로 보정하였다. 유량 예측을 위한 식은 다음과 같다.

(7)

f l o w_{t + n} = f (f l o w_{t, \dots, t - m}, r a i n f a l l_{i, t, \dots, t - m}), i = 1, 2, 3

여기서, n은 예측 시간, m은 입력 자료의 선행 시간, 그리고 i는 강우 관측소 개수이다. Gholami et al. (2015)에 따르면 일반적으로 총 데이터의 70 - 80%는 모형의 학습에, 그리고 20 - 30%는 검증 및 평가에 사용된다. 따라서, 본 연구에서는 2013년 1월 1일부터 2017년 12월 31일까지의 관측 유입량 및 강우량 자료를 이용하여 모형을 학습한 후, 2018년 1월 1일부터 2019년 12월 31일까지의 댐 유입량을 예측 및 평가하였다. 또한 모형의 구축을 위해 m = 6, n = 1값을 이용하였다.

2.4 평가 지표

본 연구에서는 모델의 예측력을 평가하기 위한 평가 지표로는 상관계수(CC), Nash-Sutcliffe 효율계수(NSE), 평균편차비율(PBIAS), 그리고 첨두값 오차(PE)를 사용하였으며, 각각에 대한 지표들을 Eqs. (8) ~ (11)에 나타내었다.

(8)

C C = \frac{\sum_{} (O_{t} - {\bar{O}}_{t}) (M_{t} - M_{t})}{\sqrt{\sum_{} {(O_{t} - O_{t})}^{2}} \sqrt{\sum_{} {(M_{t} - M_{t})}^{2}}}

(9)

N S E = 1 - \frac{\sum_{} {(O_{t} - M_{t})}^{2}}{\sum_{} {(O_{t} - O_{t})}^{2}}

(10)

P B I A S = \frac{\sum_{} (O_{t} - M_{t})}{\sum_{} O_{t}} \times 100

(11)

P E (%) = \frac{P e a k_{M} - P e a k_{O}}{P e a k_{O}} \times 100

여기서, O_t은 관측값, M_t은 예측값을 나타내고, $O_{t}$ , $M_{t}$ 은 관측값, 예측값의 평균, 그리고 Peak_O와 Peak_M은 유량 수문곡선의 첨두 유량값을 나타낸다.

상관계수(CC)는 관측값과 예측값 간의 상관관계의 정도를 구체적인 수치로 나타내어주는 지표이며, -1에서 1의 범위의 값을 가진다. 상관계수는 1에 가까울수록 예측값이 관측값과 양의 상관관계가 강함을 의미하고, -1에 가까울수록 음의 상관관계가 강함을 의미한다. NSE는 관측값 간의 차이에 대비하여 관측값과 모의값의 차이를 비교하여 정규화한 무차원의 통계지표이다(Jeong et al., 2018). NSE는 -∞ ~ 1 사이의 범위를 가지며 1에 가까울수록 좋은 값을 의미한다(Wilcox et al., 1990; Legates and McCabe, 1999; Bang and Kim, 2018). PBIAS는 관측값과 예측값의 총량을 비교하는 기초적인 통계지표이며, PBIAS는 값이 0에 가까울수록 예측 성능이 우수함을 의미한다(Jeong et al., 2018; Kim et al., 2018). PE는 유량의 첨두값 차이를 나타내는 지표로 수문곡선 기반의 평가에서 활용될 수 있다.

3. 모형 적용 및 분석

3.1 유입량 예측을 위한 LSTM-s2s 모형의 최적화

머신러닝, 딥러닝과 같은 데이터 기반의 모형은 모형의 특성과 사용 목적에 맞는 적절한 입력 자료의 종류와 시간적 특성, 모형의 hyperparameter를 선택하는 것이 중요하다. 모형 예측 결과의 성능은 입력 자료의 특성과 모형의 hyperparameter를 이용한 학습 성능을 기반으로 하기 때문에 모형 학습 전 최적의 입력 자료와 매개변수 선정 과정이 필요하다. 또한, 일반적으로 hyperparameter의 값이 클수록 자료의 복잡성을 학습하는데 유리하지만, 과적합(overfitting) 문제가 발생할 수 있기 때문에 모형 학습을 위한 적절한 매개변수 값을 설정하는 것이 매우 중요하다.

본 연구에서는 모형을 학습하는데 사용되는 입력 자료인 강우의 시간 길이(sequence length)를 결정하기 위해 2시간부터 10시간 범위에 대한 입력 자료를 평가하였다. 또한, LSTM-s2s 모형의 최적화를 위해 모형의 3가지 hyperparameters인 layers 개수, batch size, 그리고 epoch size를 각각 변화시켜 모형의 예측 성능을 확인하였다. 각 hyperparameter는 서로 복합적으로 작용하기 때문에 본 연구에서는 hyperparameter의 조합에 따른 결과의 평균값을 평가에 이용하였다. 예를 들어, 2hours-sequence length의 경우, 나머지 3가지 hyperparameters의 조합에 따른 모의 결과의 평균치를 이용하였다. 성능 평가를 위해서는 CC, NSE 그리고 PBIAS를 이용하였다. Fig. 3은 각 hyperparameter에 따른 모형의 성능을 나타내고 있다.

모형의 최적화 과정을 통해 결정된 각 매개변수는 sequence length는 6시간, layer 개수는 64개, batch size와 epoch size는 각각 96, 250개로 설정되었고, 결정된 매개변수를 기반으로 모형의 학습을 수행하였다. 각 매개변수에 대한 3가지 평가 지표의 값은 CC는 0.75, NSE는 0.45, 그리고 PBIAS는 22%로 나타나 각 매개변수를 이용하여 유입량 예측에 대한 모형의 적용 가능성을 확인할 수 있었다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-03/N0200540302/images/kwra_54_03_02_F3.jpg

Fig. 3.

Optimization results of different parameters. Each plot shows model performances using three evaluation metrics. (a) ‒ (d) indicate evaluation results for different four hyperparameters, including sequence length, number of layers, batch size, and epoch size

3.2 LSTM-s2s 모형을 활용한 댐 유입량 예측

3.2.1 예측 유입량의 비교 분석

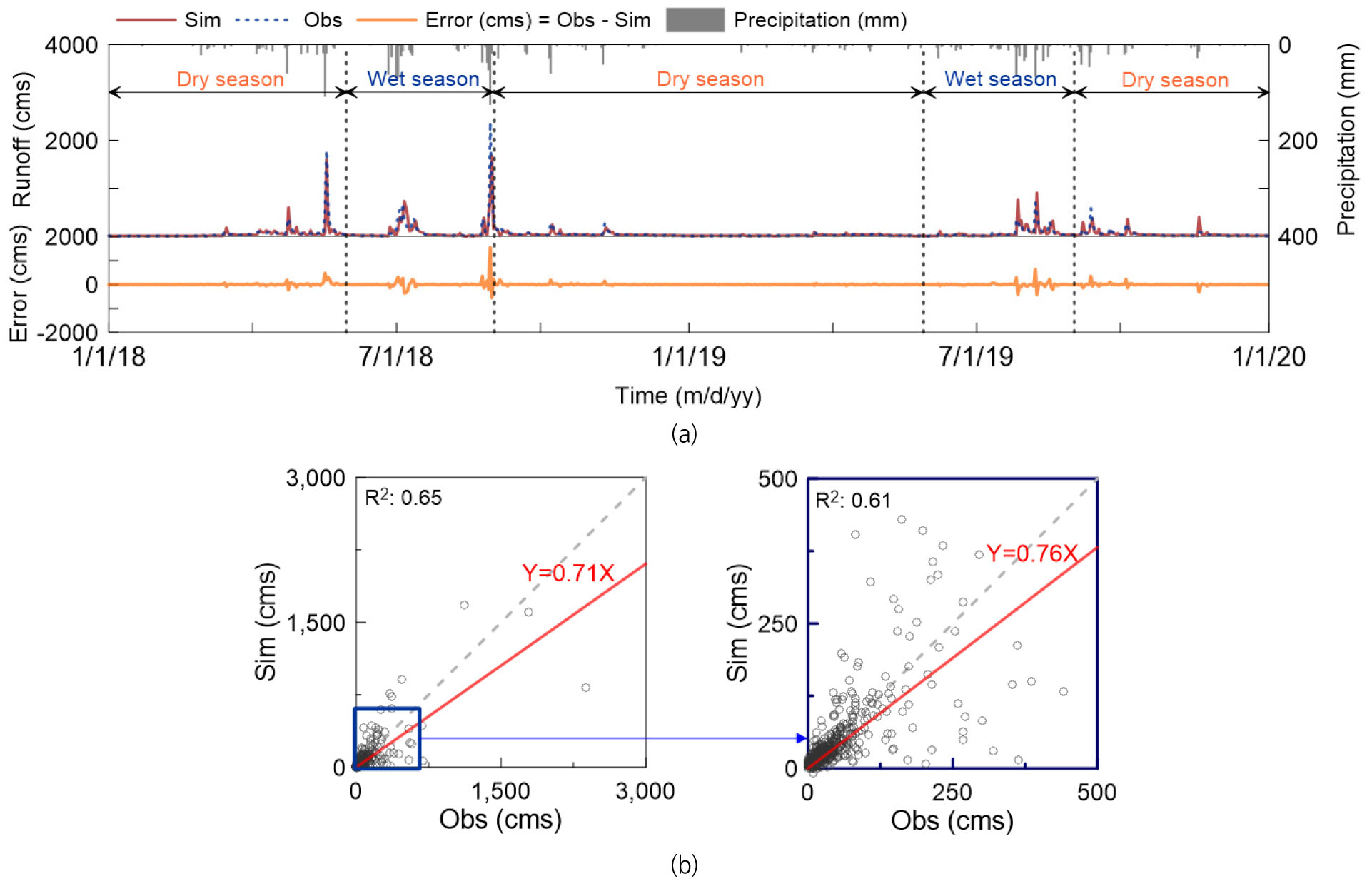
본 연구에서는 학습된 LSTM-s2s 모형을 적용하여 2018년부터 2019년까지 댐의 일 유입량을 예측하였다. 이를 위해 모형의 입력값으로는 2018년 1월-2019년 12월 사이에 관측된 일강우량과 댐의 일유입량을 이용하였다. Fig. 4는 예측기간 동안의 관측 유입량과 학습된 LSTM-s2s 모형을 이용한 예측 유입량의 시계열 자료와 분포도를 나타내고 있다. Fig. 4(a)에서 볼 수 있듯이, 예측된 유입량은 관측 유입량의 값과 변동성을 유사하게 모의하는 것으로 나타났다. Fig. 4(b)에서 전체 유입량에 대한 예측값의 R²값은 0.65로, 저유량의 경우는 0.61로 분석되었고, 최대 오차값은 1,550 cms로 나타났다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-03/N0200540302/images/kwra_54_03_02_F4.jpg

Fig. 4.

Comparison of observed and predicted inflow with lead time of 1 day from LSTM-s2s model, (a) time-series of observed and predicted inflows and (b) scatter plots of two inflows. Blue rectangle represents a scatter plot for inflows ranged between 0 ‒ 500 cms

관측 유입량 대비 예측값에 대한 정확도를 평가하기 위해 본 연구에서는 3가지 지수를 이용하였는데, 그 값은 CC가 0.78, NSE가 0.46, 그리고 PBIAS는 26.5%로 나타났다. 이는 LSTM-s2s 모형으로부터 예측된 유입량은 관측 유입량의 전반적인 경향성을 매우 비슷하게 반영하였고, 전체 유입량은 관측 대비 약 26.5%의 차이를 보이는 결과를 알 수 있었다. Table 1은 홍수기(6월 - 9월)와 이수기(10월 - 5월)에 대한 평가 결과를 나타내고 있다. 홍수기 보다 이수기 시즌에 대한 모형의 예측 성능이 보다 높게 나타났는데, 그 차이는 NSE에서 크게 나타난 반면에, CC와 PBIAS 결과는 두 시즌 모두 비교적 높은 성능의 결과를 보이고 있다. Xiang et al. (2020), Moriasi et al. (2007)에 따르면, NSE > 0.5에 대한 평가 결과는 해당 모형을 이용한 수문학적 분석 성능이 높음을 의미한다. 따라서, 이러한 결과는 LSTM-s2s 모형을 이용하여 홍수기보다 이수기에 대한 유입량 예측에 더 효율적인 것을 보여주고 있다.

Table 1.

Evaluation results for wet and dry seasons

Seasons	CC	NSE	PBIAS (%)
Wet season	0.71	0.28	29.51
Dry season	0.90	0.76	22.43

3.2.2 단일 수문곡선 기반의 유입량 예측 평가

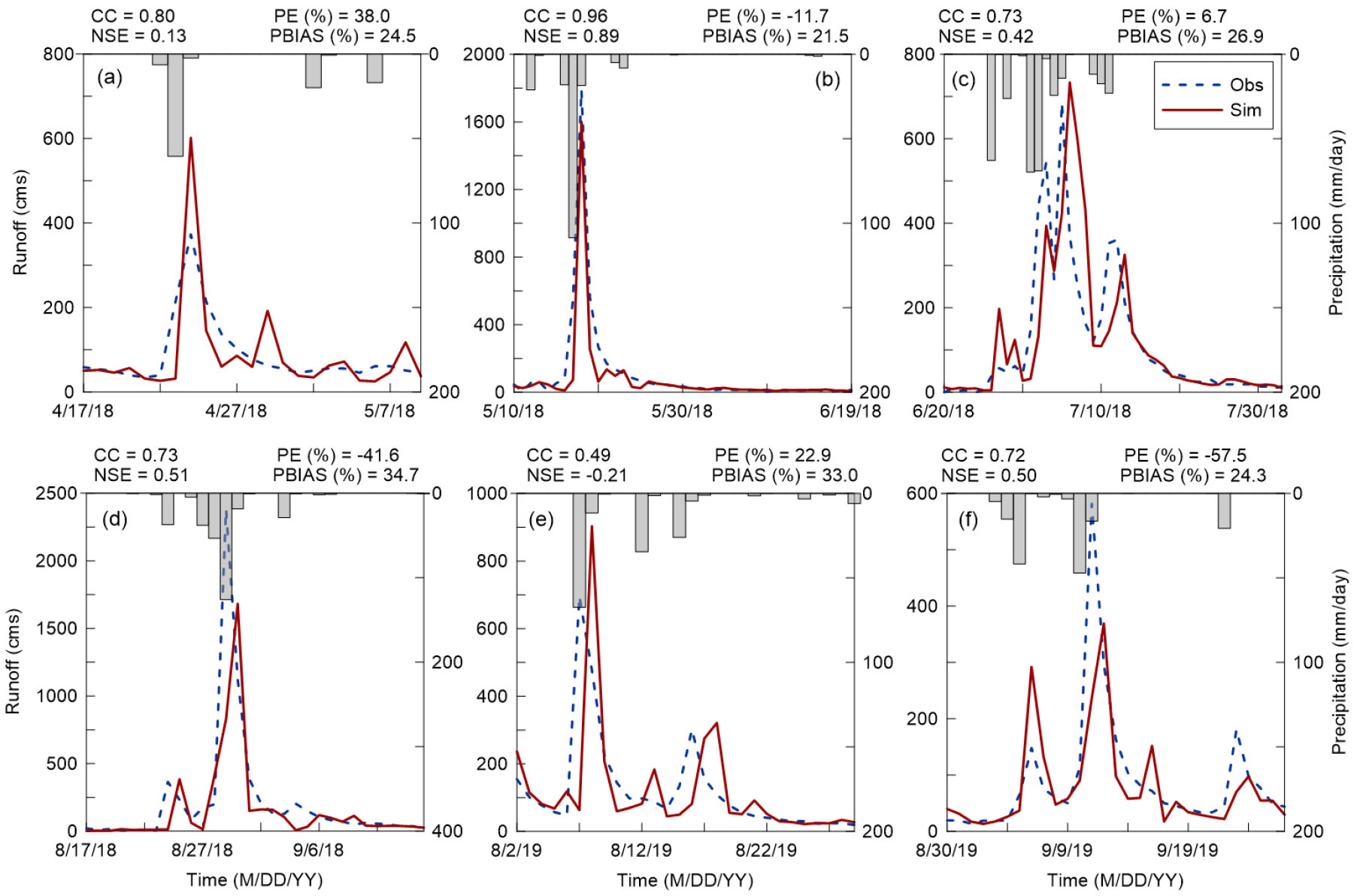
댐 유입량의 양과 첨두 유량값은 댐 운영과정에서 매우 중요한 요소이다. 특히, 효율적인 홍수 및 수자원 관리를 위해서는 보다 정확한 예측이 요구되는 바이다. 본 연구에서는 LSTM-s2s 모형을 이용한 유입량 예측 결과를 각 수문곡선에 대해 평가 하였다. 전체 유입량 곡선에서 수문곡선 분리를 위해서 곡선의 기울기 변화를 기반으로 수문곡선을 분리하였다. 기울기의 변화에 따라 각 수문곡선의 시작 및 종료 지점을 결정한 후, 첨두 유량을 결정하였다. 여기서 첨두 유량값이 전체 유입량의 평균 이상인 경우, 수문곡선으로 결정하였고, 예측기간 동안 총 19개의 수문곡선으로 구분되었다. Fig. 5는 19개의 수문곡선 중에서 유입량의 값이 상대적으로 큰 6개의 수문곡선에 대한 관측 및 예측 유입량을 나타내고 있다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-03/N0200540302/images/kwra_54_03_02_F5.jpg

Fig. 5.

Observed and predicted hydrographs from LSTM-s2s model at the validation stage in 6 runoff events

그림에서 볼 수 있듯이, 6개 유량 수문곡선에 대한 LSTM-s2s 모형의 모의 성능은 비교적 높은 것을 확인할 수 있었다. 특히, 유량의 양과 변동성을 전반적으로 잘 모의할 뿐만 아니라 첨두 유량이 발생한 시간을 잘 예측하는 결과를 보였다. 하지만, 첨두 유량값에 대한 모의 성능을 나타내는 PE (%)값은 최대 57%로 나타나 첨두 유량값에 대한 성능은 다소 낮은 것을 확인 할 수 있었다. 6개의 수문곡선 중에서 일 유입량이 1000 cms를 넘는 경우는 2개(b, d)로 나타났고, 이 수문곡선들에 대한 CC는 0.73, 0.96, NSE는 0.51, 0.89로 나타나 LSTM-s2s 모형의 높은 예측력을 확인할 수 있었다. 다만, 첨두 유량값에 대한 오차가 -11%, -41%로 산정되었는데, 이는 모형이 관측 대비 다소 과소 추정하는 결과를 나타내고 있다. 첨두 유량에 대한 예측 결과 6개의 수문곡선 중 3개의 수문곡선이 관측 대비 약 22% 과대 추정하였고, 나머지 3개 수문곡선은 약 36% 과소 추정하는 것으로 나타났다.

효율적인 댐 운영을 위해서는 2개 이상의 크고 작은 수문곡선으로 구성된 복합 수문 곡선에 대한 높은 모의 성능이 필요하다. 6개의 수문곡선 중에서, c, d, e, f의 경우는 2개 이상의 유량 수문곡선으로 구성된 복합 수문곡선의 특성을 보이는데, LSTM-s2s 모형은 이러한 수문곡선의 유량의 부피와 시간적 변동성을 비교적 잘 모의하는 것으로 나타난 반면에, 첨두 유량값에 대한 모의 결과는 다소 낮은 것을 확인 할 수 있었다.

4. 요약 및 결론

본 연구에서는 소양강댐의 유입량을 예측하기 위해 시계열 자료 예측에 높은 성능을 보이는 LSTM-s2s 모형을 적용하였다. 댐의 유입량 예측을 위해서 2013년부터 2019년까지의 소양강댐에서 관측된 유입량과 지상강우관측 지점인 인제, 홍천 그리고 춘천에서 관측된 강우량 자료를 사용하였으며, 도출된 결과를 요약하면 다음과 같다.

1) LSTM-s2s 모형으로부터 예측된 댐 유입량은 관측 유입량의 전체적인 특성과 비슷한 결과를 보였다. 예측된 유입량과 관측 유입량을 비교하였을 때, 전반적으로 유입량의 변동성을 잘 모의하였을 뿐만 아니라 총 유입량에 대한 모의 결과의 높은 예측 성능을 확인할 수 있었다. 다만, 최대 유입량이 관측된 시점에 대해서는 예측 성능이 다른 시점에 비해 다소 떨어진 것을 확인할 수 있었는데, 이는 입력변수의 종류와 모형의 최적화를 통해 해결할 수 있을 것이라 판단된다.

2) 예측기간 동안 발생 된유량 수문곡선은 총 19개로 LSTM-s2s 모형은 유량의 부피와 첨두 유량, 변동성과 같은 수문곡선 특성을 관측값과 비슷하게 모의하는 결과를 보였다. 19개 유량 수문곡선에 대한 평균 CC는 0.69, PBIAS는 24%, 그리고 PE는 37%로 나타났다. 또한 LSTM-s2s 모형은 복합 수문곡선으로 이루어진 유량에 대한 모의 성능이 높은 것으로 나타났다.

3) 홍수예방 및 수자원 관리를 위한 활용도가 높은 댐의 효율적인 운영을 위해서는 홍수기와 이수기에 대한 높은 예측 정확도가 요구된다. 본 연구에서 제시한 LSTM-s2s 모형의 댐 유입량 예측 성능은 홍수기보다는 이수기에 대해 보다 높은 결과를 보였지만, 홍수기의 유입량 역시 시간적 변동성 및 전반적인 예측 성능을 확인 할 수 있었다. 이러한 결과는 LSTM-s2s 모형이 효율적인 댐 운영을 위한 복잡한 물리적 과정을 기반으로 하는 수문모형의 대안이 될 수 있는 점을 의미한다.

LSTM-s2s 모형은 댐 유입량 예측에 전반적으로 높은 성능을 제공하는 것으로 나타났다. 본 연구에서는 댐 유입량 예측을 위해 주변 관측 지점의 강우와 댐의 과거 유입량 자료를 입력 자료로 활용하였지만, 유입량과 관련된 다양한 인자들을 모형의 추가 입력 자료로 활용한다면 보다 높은 예측 결과를 얻을 수 있을 것이라 판단된다.

Acknowledgements

이 논문은 2017년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2017R1A2B3005695).

References

Abrahart, R., Kneale, P.E., and See, L.M. (2004). Neural networks for hydrological modeling. CRC Press, London, UK. 10.1201/9780203024119

Adeyemi, O., Grove, I., Peets, S., Domun, Y., and Norton, T. (2018). "Dynamic neural network modelling of soil moisture content for predictive irrigation scheduling." Sensors, Vol. 18, No. 10, pp. 3408-3429. 10.3390/s1810340830314346PMC6210977

Assem, H., Ghariba, S., Makrai, G., Johnston, P., Gill, L., and Pilla, F. (2017). "Urban water flow and water level prediction based on deep learning." Joint European conference on machine learning and knowledge discovery in databases. Springer, Skopje, Macedonia, Vol. 3, pp. 317-329. 10.1007/978-3-319-71273-4_26

Bae, Y., Kim, J., Wang, W., Yoo, Y., Jung, J., and Kim, H.S. (2019). "Monthly inflow forecasting of Soyang River dam using VARMA and machine learning models." Journal of Climate Research, Vol. 14, No. 3, pp. 183-198. (in Korean) 10.14383/cri.2019.14.3.183

Bang, Y., and Kim, S. (2018). "Development of initial design-width formulas for small streams: Case study in Western Gangwon province." Journal of the Korean Society of Hazard Mitigation, Vol. 18, No. 6, pp. 357-367. (in Korean) 10.9798/KOSHAM.2018.18.6.357

Bicknell, B.R., Imhoff, J.C., Kittle Jr, J.L., Donigian Jr, A.S., and Johanson, R.C. (1996). Hydrological simulation program-FORTRAN. User's manual for release 11. EPA, U.S.

Blöschl, G., Hall, J., Viglione, A., Perdigão. R.A., Parajka, J., Merz, B., Lun, D., Arheimer, B., Aronica, G.T., Bilibashi, A., Boháč, M., Bonacci, O., Borga, M., Čanjevac, I., Castellarin, A., Chirico, G.B., Claps, P., Frolova, N., Ganora, D., Gorbachova, L., Gül, A., Hannaford, J., Harrigan, S., Kireeva, M., Kiss, A., Kjeldsen, T.R., Kohnová, S., Koskela, J.J., Ledvinka, O., Macdonald, N., Mavrova-Guirguinova, M., Mediero, L., Merz, R., Molnar, P., Montanari, A., Murphy, C., Osuch, M., Ovcharuk, V., Radevski, I., Salinas, J.L., Sauquet, E., Šraj, M., Szolgay, J., Volpi, E., Wilson, D., Zaimi, K., and Živković, N. (2019). "Changing climate both increases and decreases European river floods." Nature, Vol. 573, No. 7772, pp. 108-111. 10.1038/s41586-019-1495-631462777

Chen, L., Singh, V.P., Lu, W., Zhang, J., Zhou, J., and Guo, S. (2016). "Streamflow forecast uncertainty evolution and its effect on real-time reservoir operation." Journal of Hydrology, Vol. 540, pp. 712-726. 10.1016/j.jhydrol.2016.06.015

Chen, P.A., Chang, L.C., and Chang, F.J. (2013). "Reinforced recurrent neural networks for multi-step-ahead flood forecasts." Journal of Hydrology, Vol. 497, pp. 71-79. 10.1016/j.jhydrol.2013.05.038

Cho, K., Van Merriënboer, B., Bahdanau, D., and Bengio, Y. (2014a). "On the properties of neural machine translation: Encoder-decoder approaches." arXiv preprint, arXiv:1409.1259v2 [cs.CL]. 10.3115/v1/W14-4012

Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., and Bengio, Y. (2014b). "Learning phrase representations using RNN encoder-decoder for statistical machine translation." arXiv preprint, arXiv:1406.1078v3 [cs.CL]. 10.3115/v1/D14-1179

Choi, C., Kim, J., Han, H., Han, D., and Kim, H.S. (2020). "Development of water level prediction models using machine learning in wetlands: A case study of Upo Wetland in South Korea." Water, Vol. 12, No. 1, pp. 93-110. 10.3390/w12010093

Devia, G.K., Ganasri, B.P., and Dwarakish, G.S. (2015). "A review on hydrological models." Aquatic Procedia, Vol. 4, pp. 1001-1007. 10.1016/j.aqpro.2015.02.126

Fan, H., Jiang, M., Xu, L., Zhu, H., Cheng, J., and Jiang, J. (2020). "Comparison of long short term memory networks and the hydrological model in runoff simulation." Water, Vol. 12, No. 1, pp. 175-189. 10.3390/w12010175

Feng, D., Fang, K., and Shen, C. (2020). "Enhancing streamflow forecast and extracting insights using long‐short term memory networks with data integration at continental scales." Water Resources Research, Vol. 56, No. 9, e2019WR026793. 10.1029/2019WR026793

Gholami, V.C.K.W., Chau, K.W., Fadaee, F., Torkaman, J., and Ghaffari, A. (2015). "Modeling of groundwater level fluctuations using dendrochronology in alluvial aquifers." Journal of Hydrology, Vol. 529, pp. 1060-1069. 10.1016/j.jhydrol.2015.09.028

Ghumman, A.R., Ghazaw, Y.M., Sohail, A.R., and Watanabe, K. (2011). "Runoff forecasting by artificial neural network and conventional model." Alexandria Engineering Journal, Vol. 50, No. 4, pp. 345-350. 10.1016/j.aej.2012.01.005

Granata, F., Gargano, R., and De Marinis, G. (2016). "Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA's storm water management model." Water, Vol. 8, No. 3, pp. 69-81. 10.3390/w8030069

Han, J., Lee, D., Kang, B., Chung, S., Jang, W., Lim, K., and Kim, J. (2017). "Potential impacts of future extreme storm events on streamflow and sediment in Soyang-dam watershed." Journal of Korean Society on Water Environment, Vol. 33, No. 2, pp. 160-169. (in Korean)

Hu, C., Wu, Q., Li, H., Jian, S., Li, N., and Lou, Z. (2018). "Deep learning with a long short-term memory networks approach for rainfall-runoff simulation." Water, Vol. 10, No. 11, pp. 1543-1558. 10.3390/w10111543

Jeong, E., Cho, H., and Koo, B. (2018). "Analysis of the impact of droughts on river flows in an agricultural watershed using a semi-distributed watershed model STREAM." Journal of the Korean Society for Marine Environment & Energy, Vol. 21, No. 4, pp. 398-410. (in Korean) 10.7846/JKOSMEE.2018.21.4.398

Jung, S.H., Lee, D.E., and Lee, K.S. (2018). "Prediction of river water level using deep-learning open library." Journal of the Korean Society of Hazard Mitigation, Vol. 18, No. 1, pp. 1-11. (in Korean) 10.9798/KOSHAM.2018.18.1.1

Kang, N.R., Noh, H.S., Lee, J.S., Lim, S.H., and Kim, H.S. (2013). "Runoff simulation of an urban drainage system using radar rainfall data." Journal of Wetlands Research, Vol. 15, No. 3, pp. 413-422. (in Korean) 10.17663/JWR.2013.15.3.413

Kim, B.K., Kim, S.D., Lee, E.T., and Kim, H.S. (2007). "Methodology for estimating ranges of SWAT model parameters: Application to Imha Lake inflow and suspended sediments." Journal of the Korean Society of Civil Engineers, Vol. 27, No. 6B, pp. 661-668. (in Korean)

Kim, D., Kim, J., Kwak, J., Necesito, I.V., Kim, J., and Kim, H.S. (2020). "Development of water level prediction models using deep neural network in mountain wetlands." Journal of Wetlands Research, Vol. 22, No. 2, pp. 106-112. (in Korean)

Kim, K.S. (2010). A study on the real time forecasting for monthly inflow Daecheong dam using hydrologic time series analyses. Master Thesis, Seokyeong University, pp. 32-54. (in Korean)

Kim, Y., Seo, S., and Kim, Y. (2018). "Development of a hybrid regionalization model for estimation of hydrological model parameters for ungauged watersheds." Journal of Korea Water Resources Association, Vol. 51, No. 8, pp. 677-686. (in Korean)

Kratzert, F., Klotz, D., Brenner, C., Schulz, K., and Herrnegger, M. (2018). "Rainfall-runoff modelling using long short-term memory (LSTM) networks." Hydrology and Earth System Sciences, Vol. 22, No. 11, pp. 6005-6022. 10.5194/hess-22-6005-2018

Lee, G., Jung, S., and Lee, D. (2018). "Comparison of physics-based and data-driven models for streamflow simulation of the Mekong River." Journal of Korea Water Resources Association, Vol. 51, No. 6, pp. 503-514.

Lee, K., Choi, C., Shin, D.H., and Kim, H.S. (2020). "Prediction of heavy rain damage using deep learning." Water, Vol. 12, No. 7, pp. 1942-1959. 10.3390/w12071942

Legates, D.R., and McCabe, G.J. (1999). "Evaluating the use of "goodness-of-fit" measures in hydrologic and hydroclimatic model validation." Water Resources Research, Vol. 35, No. 1, pp. 233-241. 10.1029/1998WR900018

Mok, J.Y., Choi, J.H., and Moon, Y.I. (2020). "Prediction of multipurpose dam inflow using deep learning." Journal of Korea Water Resources Association, Vol. 53, No. 2, pp. 97-105. (in Korean)

Montanari, A., Rosso, R., and Taqqu, M.S. (1997). "Fractionally differenced ARIMA models applied to hydrologic time series: Identification, estimation, and simulation." Water Resources Research, Vol. 33, No. 5, pp. 1035-1044. 10.1029/97WR00043

Moriasi, D.N., Arnold, J.G., Van Liew, M.W., Bingner, R.L., Harmel, R. D., and Veith, T.L. (2007). "Model evaluation guidelines for systematic quantification of accuracy in watershed simulations." Transactions of the ASABE, Vol. 50, No. 3, pp. 885-900. 10.13031/2013.23153

Mosavi, A., Ozturk, P., and Chau, K.W. (2018). "Flood prediction using machine learning models: Literature review." Water, Vol. 10, No. 11, p. 1536. 10.3390/w10111536

Neitsch, S.L., Arnold, J.G., Kiniry, J.R., and Williams, J.R. (2011). Soil and water assessment tool theoretical documentation version 2009. Texas Water Resources Institute, Temple, TX.

Noh, H., Lee, J., Kang, N., Lee, D., Kim, H. S., and Kim, S. (2016). "Long-term simulation of daily streamflow using radar rainfall and the SWAT model: A case study of the Gamcheon basin of the Nakdong River, Korea." Advances in Meteorology, Vol. 2016, pp. 431-442. 10.1155/2016/2485251

Palmer, M., and Ruhi, A. (2019). "Linkages between flow regime, biota, and ecosystem processes: Implications for river restoration." Science, Vol. 365, No. 6459, eaaw2087. 10.1126/science.aaw208731604208

Park, M.K., Yoon, Y.S., Lee, H.H., and Kim, J.H. (2018). "Application of recurrent neural network for inflow prediction into multi-purpose dam basin." Journal of Korea Water Resources Association, Vol. 51, No. 12, pp. 1217-1227. (in Korean)

Riad, S., Mania, J., Bouchaou, L., and Najjar, Y. (2004). "Predicting catchment flow in a semi‐arid region via an artificial neural network technique." Hydrological Processes, Vol. 18, No. 13, pp. 2387-2393. 10.1002/hyp.1469

Shoaib, M., Shamseldin, A.Y., Melville, B.W., and Khan, M.M. (2016). "A comparison between wavelet based static and dynamic neural network approaches for runoff prediction." Journal of Hydrology, Vol. 535, pp. 211-225. 10.1016/j.jhydrol.2016.01.076

Sutskever, I., Vinyals, O., and Le, Q.V. (2014). "Sequence to sequence learning with neural networks." arXiv preprint, arXiv:1409. 3215v3 [cs.CL].

Tian, Y., Xu, Y.P., Yang, Z., Wang, G., and Zhu, Q. (2018). "Integration of a parsimonious hydrological model with recurrent neural networks for improved streamflow forecasting." Water, Vol. 10, No. 11, pp. 1655. 10.3390/w10111655

Wilcox, B.P., Rawls, W.J., Brakensiek, D.L., and Ross Wight, J. (1990). "Predicting runoff from rangeland catchments: A comparison of two models." Water Resources Research, Vol. 26, No. 10, pp. 2401-2410. 10.1029/WR026i010p02401

Xiang, Z., Yan, J., and Demir, I. (2020). "A rainfall-runoff model with LSTM-based sequence‐to‐sequence learning." Water Resources Research, Vol. 56, No. 1, e2019WR025326. 10.1029/2019WR025326

Xu, J., Luo, W., and Huang, Y. (2019). "Dadu River runoff forecasting via Seq2Seq." Proceedings of the 2019 International Conference on Artificial Intelligence and Computer Science, Wuhan, China, pp. 494-498. 10.1145/3349341.3349457

Yan, J., Jin, J., Chen, F., Yu, G., Yin, H., and Wang, W. (2018). "Urban flash flood forecast using support vector machine and numerical simulation." Journal of Hydroinformatics, Vol. 20, No. 1, pp. 221-231. 10.2166/hydro.2017.175

Zhang, J., Zhu, Y., Zhang, X., Ye, M., and Yang, J. (2018). "Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas." Journal of Hydrology, Vol. 561, pp. 918-929. 10.1016/j.jhydrol.2018.04.065

Zhang, Q., Xiao, M., Singh, V.P., and Li, J. (2012). "Regionalization and spatial changing properties of droughts across the Pearl River basin, China." Journal of Hydrology, Vol. 472, pp. 355-366. 10.1016/j.jhydrol.2012.09.054

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Application of sequence to sequence learning based LSTM model (LSTM-s2s) for forecasting dam inflow

ABSTRACT

MAIN

Fig. 1.

Study area of this study; Soyang River dam watershed

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 2.

Conceptual diagram of LSTM cells and LSTM-s2s model

(7)

(8)

(9)

(10)

(11)

Fig. 3.

Optimization results of different parameters. Each plot shows model performances using three evaluation metrics. (a) ‒ (d) indicate evaluation results for different four hyperparameters, including sequence length, number of layers, batch size, and epoch size

Fig. 4.

Comparison of observed and predicted inflow with lead time of 1 day from LSTM-s2s model, (a) time-series of observed and predicted inflows and (b) scatter plots of two inflows. Blue rectangle represents a scatter plot for inflows ranged between 0 ‒ 500 cms

Table 1.

Evaluation results for wet and dry seasons

Fig. 5.

Observed and predicted hydrographs from LSTM-s2s model at the validation stage in 6 runoff events

Acknowledgements

References