1. 서 론
기존의 물 사용량 측정은 검침원이 일일이 개별 수용가의 수도계량기를 확인하는 방식으로 수행되었다. 이러한 인력 검침방식은 비용 효율성, 검침관리의 어려움, 사생활 침해 문제를 야기할 뿐만 아니라 낮은 측정 빈도로 인해 해당 데이터의 물 수요관리에 활용을 어렵게 하였다. 이에 최근에는 실시간 원격으로 다양한 수리 및 수질변수를 측정하는 스마트미터(Smart meter)가 대두되고 있다.
국외(미국, 이스라엘, 캐나다, 유럽 등)에서는 스마트미터를 적용한 물 수요관리가 이루어지고 있으며(Joo et al., 2012b), 우리나라도 스마트워터시티 사업 추진을 통해 물 공급의 전 과정에 대해서 ICT (Information and Communication Technology)를 접목하여 수량 및 수질을 실시간으로 관리하고 정보를 제공하고 있다. K-water에서는 2014년 파주시의 일부 지역에 대해서 스마트워터시티 시범사업을 진행하였고, 2016년에는 파주시 전 지역으로 확대 추진되었다(Kim, 2015). 해당 사업을 통해서, 수질의 개선과 수돗물의 직접 음용률이 1%에서 36.3%로 개선되었으며, 파주시를 시작으로 송산그린시티 및 부산에코델타시티 등에서는 건설 단계에서부터 스마트워터시티를 적용하였다. 2017년에는 환경부, 세종시 그리고 K-water가 총사업비 120억 원을 투입한 최초의 스마트워터시티 구축 국가사업에 착수하였다. 해당 기반시설에는 원격 누수감지센터 1,300대, 스마트수도미터 926대, 실시간 수질계측기 8기 등의 설치를 목표로 하고 지난 2020년 시범사업이 완료되었다. 환경부에서는 총 사업이 약 1조 4천억 원의 규모로 2022년까지 스마트상수도 구축사업을 전국으로 확대할 예정이다.
스마트미터는 계측 주기가 짧고 계측 밀도가 높아 각 수용가별 사용량이 초분 단위로 측정되어 SCADA (Supervisory Control and Data Acquisition) 관제시스템에 송신된다. 물 공급자는 이 데이터를 이용하여 개별 수용가의 수요관리 정보를 제공할 수도 있고, 구역별로 합하여 전체 상수도관망의 운영 및 관리에 활용할 수도 있다. 스마트미터 데이터를 보다 효율적으로 활용하기 위해서는 각 목적에 적합한 분석기법을 적용하여 데이터에 담긴 유의미한 정보를 효과적으로 추출하는 것이 중요하다.
스마트미터가 도입된 이후, 스마트미터 데이터를 상수도관망 운영 및 관리에 활용한 연구가 국내․외에서 활발히 수행되었다. 국외에서는 다양한 기계학습법(Machine Learning)을 적용하여 사용자의 물 수요량을 예측하였다(Pesantez et al., 2020; Xenochristou et al. 2021). 또한, 개별 가구 규모에서 스마트미터 데이터를 이용하여 사용자의 물 사용 패턴을 분석하는 연구가 수행되었다(Cominola et al., 2019; Nguyen et al., 2015). 국내에서는 인천시에 설치된 스마트미터에서 측정된 일별 및 계절별 물 사용량 자료를 추세분석하여 1인 1일 용수 사용량을 산출하였으며(Joo et al., 2012a) 선형회귀분석 방법을 적용하여 주거용수의 요일별 및 월별 사용 모형을 개발하였다(Kim, 2012). 또한, 기계학습법을 이용하여 미터기 오류의 판별, 물 사용량 예측, 용도별(가정용, 상업용) 물 사용 예측에 관한 연구를 수행하였다(Choi and Kim, 2018).
이처럼 스마트미터 데이터와 관련된 다양한 연구들이 수행되었으나, 가구별 물 사용량이 갖는 높은 공간 해상도 특성을 분석하여 스마트미터 데이터를 분류한 연구는 미비하였다. 국외에서는 최근 최종 물 사용(예: 샤워기, 싱크대 등) 분류에 관한 연구를 수행한 바 있다(Gourmelon et al., 2021). 하지만 해당 연구는 실제 데이터가 아닌 사용자 물 수요량 시뮬레이션 모형으로 생성한 가공 데이터(Synthetic data)를 이용하였으며, 스마트미터로부터 실제 측정된 물 수요 데이터의 특성을 분석하여 비슷한 물 사용 패턴을 갖는 가구를 분류하는 기법을 제안한 연구는 아직 미비하다. 가구별 물 사용 패턴을 실시간으로 분석하고 분류할 수 있다면 물 공급 시스템의 운영관리기술을 향상시킬 수 있고 수요자의 비정상적인 수요 패턴(누수 등)을 신속하게 파악하여 물 손실 비용을 절감할 수 있다.
기존의 물 사용 분류는 스마트미터의 배터리 및 통신 문제로 인해 결측 및 오측 데이터가 발생하게 될 경우, 어디서부터 온 데이터인지 알 수가 없다. 즉, 스마트미터 데이터가 가구별로 분류되어 들어오지 않는 경우 이러한 데이터들은 특정 가구의 데이터로 반영되지 않고 폐기된다. 만일 각 가구별 물 사용량을 분석하여 가구별 수요 패턴을 파악한 후, 가구별로 라벨링 되어 들어오지 않은 데이터를 적절한 가구로 분류해준다면 데이터의 손실을 막고, 더욱 정확한 물 사용 분석이 가능할 것이다. 따라서 본 연구에서는 대표적인 비지도 기계학습법(Unsupervised Machine Learning) 중 하나인 K-means 기법을 적용하여 가구별 물 수요 패턴을 분류하였다. K-means 기법은 군집과 데이터 사이의 유클리드 거리(Euclidian distance)를 계산하여 주어진 데이터를 군집화하는 알고리즘으로 현재까지도 다양한 분야에서 데이터를 분류하는데 활발히 쓰이고 있다(Wu et al., 2021).
본 연구에서는 Buchberger and Wells (1996)의 연구에서 수집된 미국 오하이오 주 밀포드 데이터를 이용하여 (1) 가구수요량 스마트미터 데이터의 특성 및 활용법을 소개하고 (2) 데이터 특성을 이용한 가구별 물 사용량 분류 방법론을 제시한다. 해당 데이터는 밀포드의 한 거주 지역에서 1997년 4월 1일부터 10월 31일까지 21개 가구의 초단위 유입관 유량을 측정한 값이다. 원 스마트미터 데이터는 분석의 임의성을 최소화하기 위해서 일정 시간동안 지속된 일정 규모의 물 사용량을 갖는 사각형 형태의 펄스로의 변환 과정을 거친다. 펄스는 2가지의 형태로 나뉘며, 각 펄스의 강도와 지속시간 통계값은 가구별 월별 물 사용 특성을 나타낸다. 마지막으로, K-means 알고리즘을 이용하여 각 가구별 월별 데이터를 유사한 물 사용 패턴끼리 분류한다.
다음 절에서는 연구에 사용된 단어들과 데이터의 정의 및 연구에 적용된 방법론을 설명한다.
2. 데이터 및 방법론
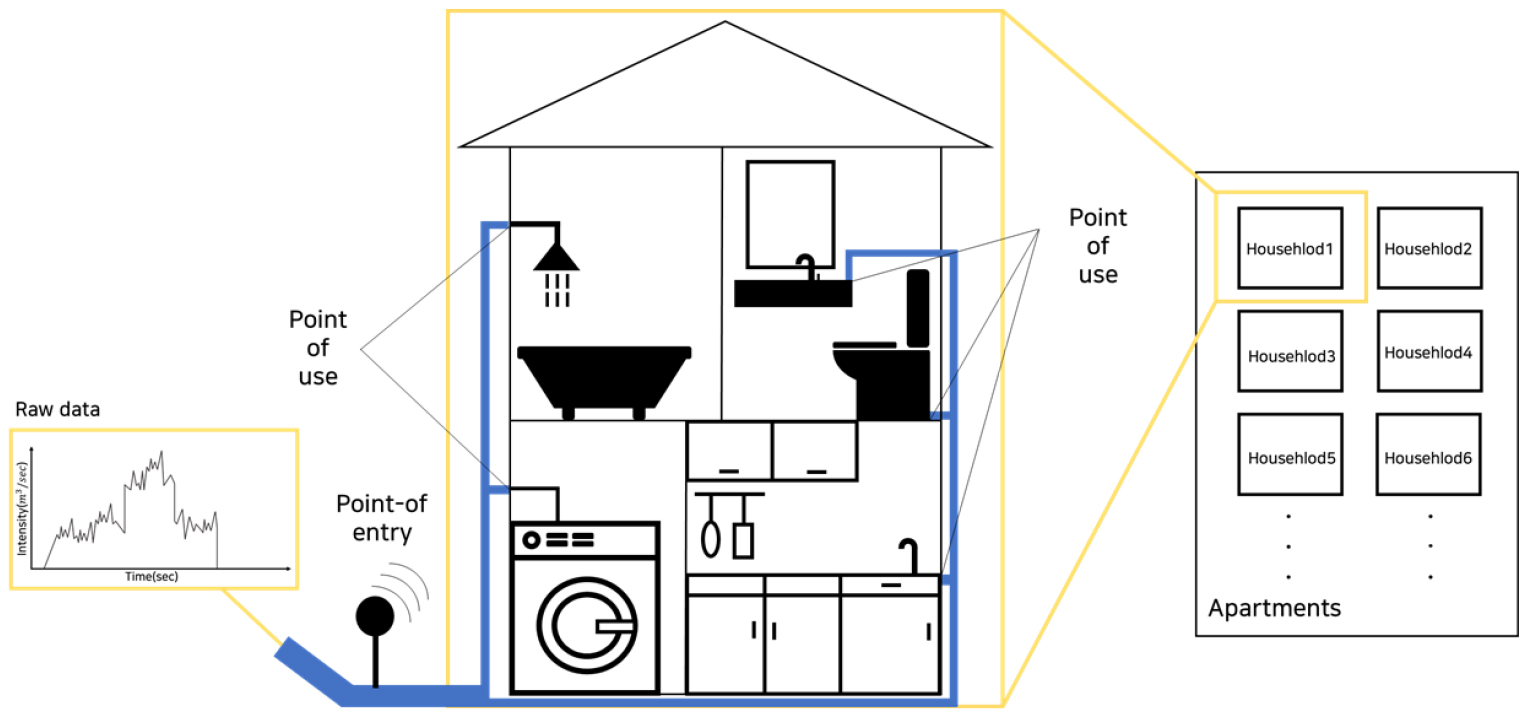
아래의 Fig. 1은 가구 내의 물의 유입, 진입점 및 사용점을 나타낸다. 배관을 통해서 가정용 용수가 들어오게 되고, 용수는 가구 내 물이 사용되는 지점에 따라서 배관을 통해 다시 나누어진다.
2.1 용어 정의
2.1.1 진입점과 사용점
진입점은 가구의 유입관에 스마트미터가 설치된 지점으로, 가구 내의 누수가 없는 경우 진입점에서의 유량은 총 가구 수요량과 동일하다. 사용점은 가구 내에서 물 사용이 발생하는 (예: 샤워기, 세면대, 싱크대, 세탁기, 변기 등) 지점을 말한다(Fig. 1). 따라서 각 사용점에서의 물 사용량을 합하면 총 가구 수요량과 같다. 즉, n은 사용점의 개수, q는 진입점으로 들어오는 물의 유입량, i는 각 사용점, quse,i는 i번째 사용점의 물 사용량, MEi는 i번째 사용점의 계측 오차(measurement error)라고 하여 Eq. (1)로 표현할 수 있다.
단일 가구 내에는 복수의 사용점이 존재하기 때문에 각기 다른 물 사용 장치(unit)의 동시 물 사용에 의해서 사용량 중첩이 발생하게 된다. 본 논문에서는 이를 동시 물 사용이라고 지칭하며, 진입점에서 수집된 데이터는 동시 물 사용 발생을 포함하고 있다.
2.1.2 원데이터(Raw data)
원데이터란 가공되지 않은 본래의 데이터를 의미한다. 스마트미터의 원데이터는 계측 오차, 사용량 자체가 가지는 변동 때문에 Fig. 1과 같이 추계학적인 특성을 가지며, 그 정도는 계측 시간 단위 및 가구 내 물 사용 장치의 종류 등에 따라 다르다. 펄스 분석의 임의성을 최소화하기 위해서는 원데이터를 평탄화하는 과정(smoothing)이 필요하다. 평탄화된 물 사용 데이터는 보다 더 뚜렷한 사각형의 펄스 형태를 가진다.
2.1.3 펄스(Pulse)
펄스는 일정 시간동안 지속된 일정 규모의 물 사용량이 도시하는 사각형 차트를 말한다. 가로축은 시간(단위: sec), 세로축은 물 사용량(물 사용 강도, 단위: m3/sec)인 그래프에 스마트미터 측정값을 시계열로 그리면, 데이터가 갖는 고해상도의 특성 및 사용량 발생 즉시 목표 사용량에 도달하는 성질 때문에 해당 그래프는 펄스 형태를 보인다. 예를 들어, 세면대의 수도꼭지를 트는 순간 사용량은 수직 상승하며 목표 사용량에 수렴하여 그 값이 지속된다. 사용을 중단하기 위해 잠그는 순간 사용량 값은 다시 0으로 떨어진다. 각 펄스의 면적은 물 사용 지속시간(duration)과 물 사용 강도(intensity)의 곱, 즉 해당 펄스에 사용된 전체 물의 용적(volume)을 의미한다. 따라서, 개별 물 사용 펄스는 지속 시간과 물 사용 강도, 2가지에 의해서 특징 지어질 수 있으며 사용점 종류에 따라 상이한 형태의 펄스가 구성된다. 예를 들어, 세면대 수도꼭지는 보통 짧은 지속 시간과 작은 물 사용 강도를 갖는 펄스가 나타나며, 세탁기 사용에 의한 물 사용 펄스는 상대적으로 지속 시간이 길며 사용 강도가 크다.
2.1.4 복합 직사각형 펄스(Strings Of Random Blocks, SORB)
복합 직사각형 펄스는 특정 지속 시간에 대해 2개 이상의 단일 직사각형 펄스가 중첩된 펄스, 즉 2개 이상의 사용점에서 물 사용이 발생하는 펄스로 정의한다. 진입점에서 얻어진 스마트미터 데이터는 보통 동시 물 사용이 발생하며 복합 직사각형 펄스는 원데이터의 불균일한 형태를 매끄럽게 바꾸어주는 과정(smoothing)을 통해서 얻을 수 있다. 본 연구의 최종 목적은 단일 직사각형 펄스를 수집하여 그에 해당하는 데이터 셋을 활용하여 가구별 물 사용량에 대한 분석을 실행하는 것이다. 따라서 복합 직사각형 펄스를 단일 직사각형 펄스로 분리하는 과정이 필요하며 본 연구에서는 Smart Meter dAta Pulse Separation (SMAPS) 룰을 적용하여 분리한다. SMAPS 방법론은 다음 절에서 자세히 설명한다.
2.1.5 단일 직사각형 펄스(Single Equivalent Rectangular Pulse, SERP)
단일 직사각형 펄스는 특정 지속 시간에 대해 한 개의 사용점에서 물 사용이 발생하는 펄스로 정의한다. 즉, 하나의 사용점에서 얻어진 스마트미터 데이터를 의미하며, 복합 직사각형 펄스에 SMAPS 룰을 적용하여 얻어진다. 단일 직사각형 펄스는 개별 사용점으로 완전히 분리된 펄스이기 때문에 이에 해당하는 데이터 셋을 활용하여 가구 내 물 사용 분석에 용이하게 사용할 수 있다. 본 논문에서 사용되는 SORB과 SERP의 개념 및 정의는 Buchberger and Wells (1996)와 University of Cincinnati의 Steven Buchberger 교수가 수행한 USEPA 연구(Buchberger et al. 2003)에서 제시된 것이다.
2.2 펄스 변환 과정
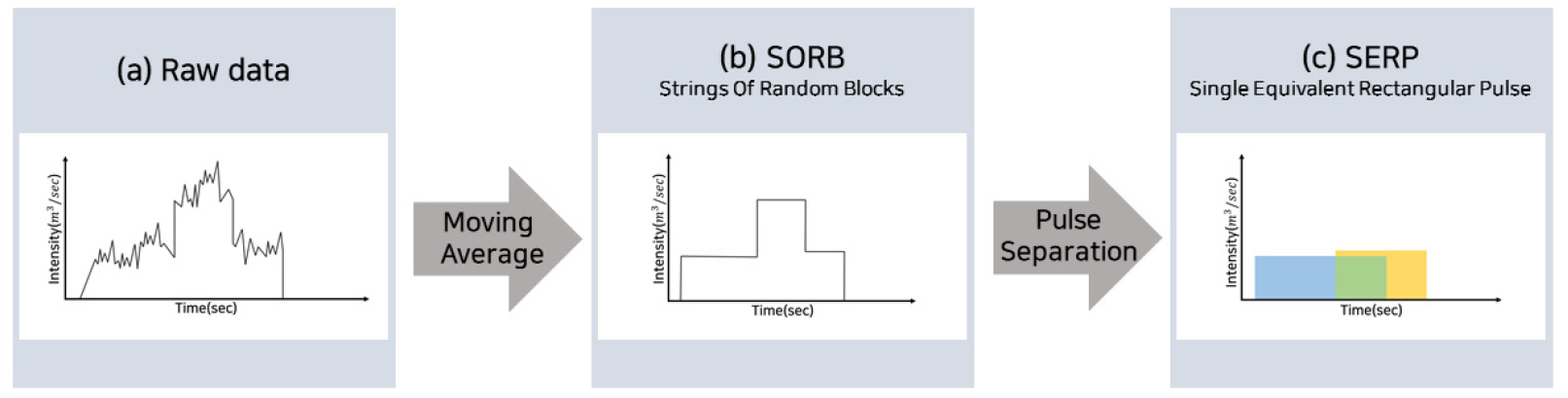
진입점에서 계측되는 원데이터는 계략적인 펄스의 형태를 띠고 있지만, 계측오차 및 자연적인 미소 변동에 의한 노이즈를 포함하고 있다(Fig. 2(a)). 따라서 가구 내 각 사용점에서의 물 사용량을 나타내는 단일 직사각형 펄스로 분리하기 위해서는 원데이터의 평활화(smoothing) 작업이 필요하다. 본 연구에서는 이동 평균법을 이용하여 원데이터를 복합 직사각형 펄스로 변환(Fig. 2(b))하였다. 복합 직사각형 펄스를 도출한 후, 이를 본 연구에서 개발한 SMAPS 룰을 적용하여 단일 직사각형 펄스, 즉 개별 사용점 펄스(Fig. 2(c))로 분리한다. 원데이터로부터의 펄스들이 단일 직사각형으로 구분되는 개수에 따라 최종 수요량의 분류가 달라질 수 있다. Fig. 2는 위에서 상기한 전체 펄스 변환 과정의 모식도이다.
2.2.1 이동평균법
이동평균법은 시계열 데이터를 대상으로 일정기간별 평균을 계산하여 시계열 데이터를 평활하게 만들어주는 것을 말한다. 평균 물 사용 강도를 , 선택한 시간 간격을 T, 시작 시간을 Ts, 종료 시간을 Te, 해당 시간의 물 사용 강도를 I(t)라고 하면 평균 물 사용 강도는 Eq. (2)와 같이 표현할 수 있다.
이때, 이동평균의 평활화(smoothing) 정도는 평균 계산을 위해 고려하는 시간 간격 T에 따라 달라진다. 따라서 스마트미터기 계측 시간 간격과 사용자가 원하는 평활화 정도에 따른 결정이 필요하다. 본 연구에서 사용된 원데이터는 1초의 시간 간격으로 물 수요량이 측정되었으며 5개의 데이터. 즉, T=4를 이용하여 이동평균법을 적용해서 원데이터를 복합 직사각형 펄스로 변환하였다.
2.2.2 적용 데이터 셋
본 연구에서는 Buchberger and Wells (1996)의 연구에서 수집된 미국 오하이오 주 밀포드 데이터 그대로를 연구에 적용하여 사용하였다. 데이터 셋은 진입점과 사용점의 데이터 셋으로 분류할 수 있다. 진입점과 사용점의 데이터 셋의 범례는 공통적으로 월, 일, 펄스 번호, 시간, 지속시간, 유량 그리고 부피를 포함한다. 데이터 셋의 구성은 아래의 Table 1과 같다. 해당 데이터 셋은 데이터 전처리(데이터 평활화 및 SMAPS 룰 적용)를 통해 얻어졌다.
펄스 번호는 X월(X는 1 ~ 12까지의 값을 가질 수 있으며 본 연구에서는 4,5,6,7,8,9,10가 사용됨)에 해당하는 한 달 동안 펄스가 계측된 횟수, 즉 물 사용 발생 횟수를 의미한다. 펄스 번호는 1 이상의 자연수가 될 수 있다. 시작 시간은 자정부터 오전 12시를 해당 펄스가 시작된 시간까지의 시간을 초로 나타낸다(0부터 86400까지의 값을 가짐). 지속 시간은 각 펄스가 시작되어 종료될 때까지 시간을 말한다. 물 사용 강도는 각 펄스 번호에 해당하는 물 사용 강도를 나타낸다. 마지막으로 부피는 각 펄스 번호에 해당하는 물 사용의 부피를 말한다.
다음 절에 기술된 펄스 변환 과정을 통해서 진입점의 데이터 셋으로부터 사용점의 데이터 셋을 얻을 수 있다.
Table 1.
Pulse data through raw data pulse transformation process
2.2.3 Smart Meter dAta Pulse Separation (SMAPS) 룰
용어 정의에서 복합 직사각형 펄스를 특정 지속 시간에 대해 2개 이상의 단일 직사각형 펄스가 중첩된 펄스로 정의했다. 따라서 복합 직사각형 펄스를 각각의 개별 단일 직사각형 펄스로 분리하는 과정이 필요하며, 분리 과정에서 SMAPS 룰이 적용된다. SMAPS 룰은 2개의 세부 룰로 나눌 수 있다.
각 데이터의 복합 직사각형 펄스 번호를 N-1, N, N+1, 펄스의 시작 시간을 T, 펄스의 지속 시간을 D, 펄스의 유량을 I라고 하고 이로부터 분리된 2개의 단일 직사각형 펄스의 지속시간을 , 펄스의 유량을 라고 한다. DN은 펄스 번호 N의 지속 시간, TN은 펄스 번호 N의 시작 시간, IN은 펄스 번호 N의 유량을 의미한다. 아래 첨자 N의 경우, N-1, N+1 등의 값을 가질 수 있으며 N은 2 이상의 모든 자연수의 값을 가질 수 있다. 동시 물 사용의 발생은 Eq. (3)을 만족한다.
즉, 특정 펄스의 시작 시간과 지속 시간을 더했을 때, 그 다음 펄스의 시작 시간과 같아야 한다는 것을 의미하며 해당 시작 시간을 기준으로 펄스의 물 사용 강도가 변화한다. 또한, 복합 직사각형 펄스에서 단일 직사각형 펄스로의 변환 과정에서는 부피는 보존된다.
SMAPS 룰은 3개의 진입점 데이터를 포함하는 복합 직사각형 펄스를 2개의 사용점 데이터를 포함하는 2개의 단일 직사각형 펄스로 분리하는 것을 기본으로 한다. 3개의 진입점 데이터를 기준으로 SMAPS 룰에서는 N번째 펄스에서 2개의 사용점의 동시 물 사용, 즉, 펄스의 중첩이 발생한다. 이때, 룰 1과 룰 2를 나누는 기준은 N-1번째 펄스와 N+1번째의 펄스가 동일한 사용점을 나타내는가 다른 사용점을 나타내는가이다. 아래에서 개별 SMAPS 룰을 설명한다.
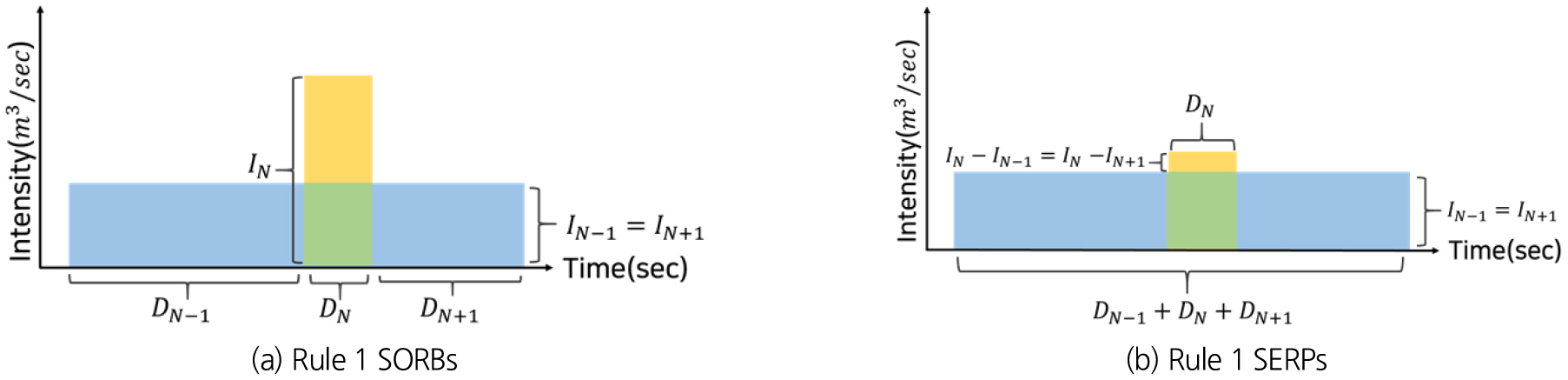
(1) 룰 1 : 이고 인 경우
룰 1은 N-1번째 펄스와 N+1번째 펄스가 동일한 사용점을 의미한다. 즉, 복합 직사각형 펄스(SORBs)의 시작 시간부터 종료 시간까지 이어지는 가로로 긴 단일 직사각형 펄스와 N번째 펄스에 해당하는 물 사용 강도에서 N-1번째 또는 N+1번째의 물 사용 강도에 해당하는 값을 뺀 물 사용 강도와 N번째 펄스의 지속 시간을 갖는 단일 직사각형 펄스(SERPs)로 분리된다는 것을 의미한다(Fig. 3). 따라서 최종적으로 분리된 2개의 단일 직사각형 펄스의 지속 시간과 물 사용 강도는 Eqs. (4a) and (4b)로 나타낼 수 있다.
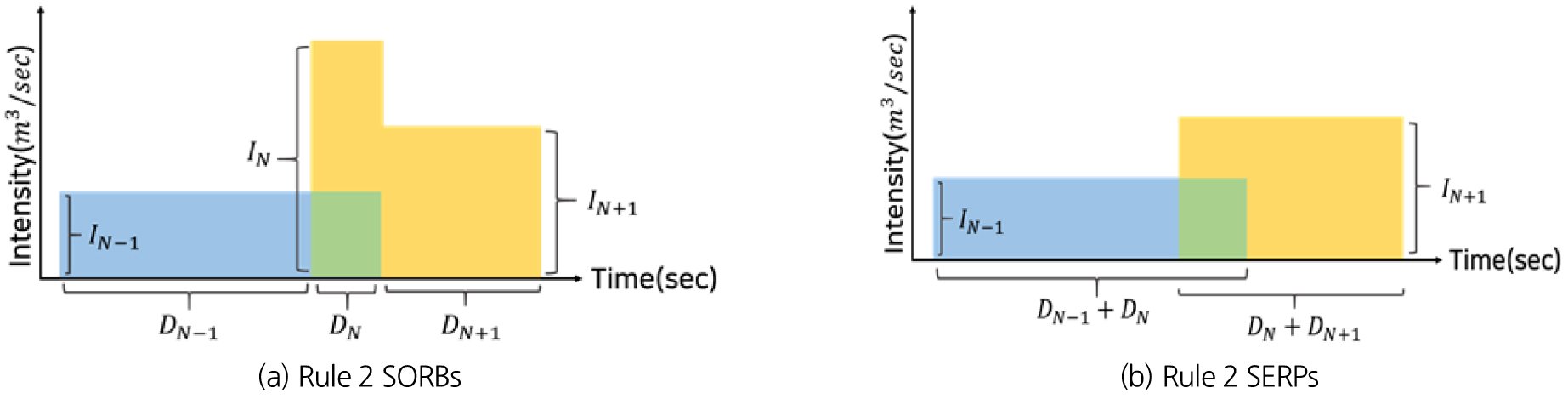
(2) 룰 2 : 이고 경우
룰 2는 N-1번째 펄스와 N+1번째 펄스가 다른 사용점을 의미한다. 즉, N번째 펄스를 기준으로 2개의 개별 사용점으로 분리되는 것을 의미한다. 룰 2를 통해서 분리되는 2개의 단일 직사각형 펄스는 N-1번째 펄스의 시작 시간으로부터 N번째 펄스의 종료 시간까지를 지속 시간, N-1번째 펄스의 물 사용 강도를 새로운 단일 직사각형 펄스의 물 사용 강도로 가지는 것과 N번째 펄스의 시작 시간으로부터 N+1번째 펄스의 종료 시간까지를 지속 시간, N+1번째 펄스의 물 사용 강도를 새로운 단일 직사각형 펄스의 물 사용 강도로 가지는 펄스로 분리된다(Fig. 4). 따라서 최종적으로 분리된 2개의 단일 직사각형 펄스의 지속 시간과 물 사용 강도는 Eqs. (5a) and (5b)로 나타낼 수 있다.
2.3 K-means
K-means는 비지도학습의 한 종류로써, 주어진 데이터들을 특정한 그룹에 속하는 군집(클러스터)으로 분할하는 기계학습법이다. K-means는 군집의 수와 개체(오브젝트)를 포함하는 집합을 입력값으로 사용하고, 출력값으로 각 개체가 속하는 군집을 얻는다. K-means는 각 집합별 중심점과 집합 내 개체간 거리의 제곱합을 비용함수로 정하고, 이 함숫값을 최소로 하는 집합을 찾는 것을 목표로 한다. 따라서 비용함수를 점차 최소화하는 방향으로 각 데이터들을 분할한 집합 내 개체들을 업데이트하면서 군집화를 수행한다.
비용함수는 Eq. (6)을 이용하여 나타낼 수 있으며, i개의 데이터를 갖는다고 가정했을 때, 식에서 는 i번째 데이터의 x좌표, 는 가 할당된 군집의 번호, 는 k번째 군집의 중심, 는 가 할당된 군집의 중심을 의미한다.
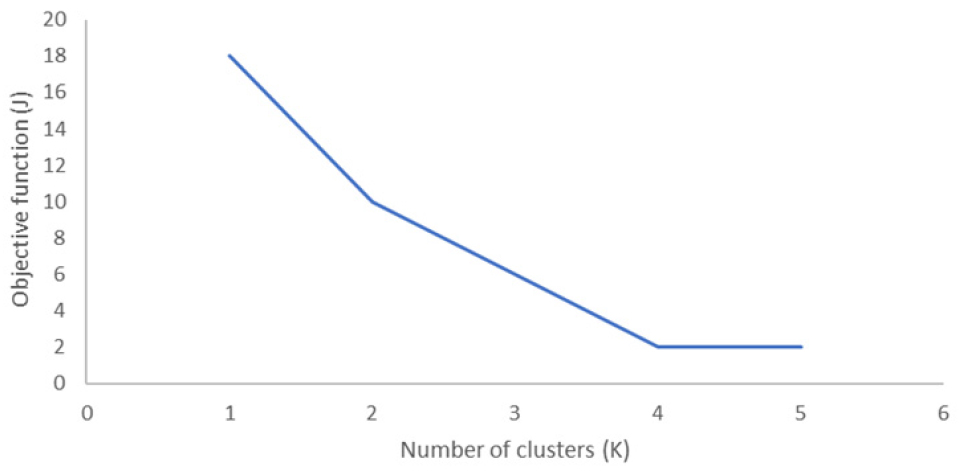
군집화를 하는데에 있어서 가장 먼저 결정해야 하는 것은 군집의 개수이다. 군집의 수는 입력받은 개체의 개수와 같거나 작은 수의 그룹으로 나눈다. 군집의 수를 결정하는 방법은 다양하며 그 중 간단한 방법 중 한 가지는 Elbow method이다. Elbow method는 군집의 개수(K)를 점차 늘려가며 그에 따른 비용함수의 그래프를 그리고 임계점(tipping point)에 도달하는 K를 군집의 수로 결정한다. Fig. 5는 Elbow method로 군집의 개수를 결정하는 하나의 예시를 보여준다. x축을 군집의 개수 (K), y축을 비용함수(J)라고 할 때, K를 1에서부터 점차 늘려가면서 해당 군집의 개수에 대한 비용함수를 계산한다. 각 K에 대한 비용함수를 그래프로 나타내면 K=4를 기점으로 비용함수가 일정한 값을 가지는 것을 확인할 수 있다. 이때, K=4인 지점을 임계점(tipping point)이라고 하며 해당 값을 군집의 수로 결정한다. 본 연구에서는 21개의 가구의 진입점 데이터를 기반으로 Elbow method를 적용하여 군집의 수를 구했다.
3. 연구 결과
본 연구는 오하이오 주 밀포드 21개 가구에서 총 7개월 동안 측정(1997년 4월에서 10월)된 단일 직사각형 펄스 데이터의 통계 특성값을 활용하여 가구별 분류(clustering)를 수행하였다. 가구별 스마트미터 데이터를 분류하기 위해서는 비지도학습법 중 하나인 K-means 알고리즘을 적용하였다. 즉, 각 데이터가 어느 가구의 데이터인지 라벨링을 제공하지 않고 동일한 가구의 데이터가 동일한 그룹으로 분류되는지 확인하였다.
3.1 사용점 데이터 셋의 변환
본 연구의 목적은 21개 가구의 사용점 데이터 셋을 기반으로 K-means 클러스터링을 통한 가구별 분류이기 때문에 기존의 데이터 셋을 적용하여 21개 가구의 일별 데이터에 대한 분류를 진행할 경우, 데이터의 양이 방대하여 어려울 것으로 예상되었다. 따라서 각 가구별 일별 지속 시간 및 물 사용 강도 데이터의 월별 통계 값을 계산하여 분류에 활용하였다. 총 5가지의 변수: (1) 지속 시간의 월평균 및 (2) 표준편차, (3) 물 사용 강도의 월평균 및 (4) 표준편차, (5) 지속 시간과 물 사용 강도의 상관계수 값을 K-means에 적용하였다.
Table 2는 21개의 가구 중에서 첫 번째 가구의 앞서 언급한 5개의 변수를 월별(4월에서 10월까지)로 계산하여 정리한 표이다. 21개의 가구 중, 대부분의 가구들은 해당 기간(1997년 4월 ~ 10월) 동안의 데이터가 존재했지만 6번째 가구의 경우는 4,6,7월의 데이터가, 9번째 가구의 경우, 4월의 데이터가 존재하지 않았다. 이처럼 데이터가 존재하지 않는 가구의 경우는 데이터가 존재하지 않는 해당 달의 데이터만 비워두고 계산을 진행하였다. 지속시간은 소수점 아래 첫째 자리까지의 결과를 나타내었으며, 물 사용 강도는 소수점 아래 셋째 자리까지의 계산 결과를 나타내었다.
Table 2.
Monthly values of 5 variables in household 1
본 연구에서는 데이터의 정규화 작업을 통해 모든 데이터들이 0과 1 사이의 값을 가지도록 한다. 먼저 각 가구별 데이터 셋을 합친 후, 정규화를 위해 각 변수별 최솟값과 최댓값을 구한다(Table 3). 최대-최소 정규화는 Eq. (7)을 따른다.
Table 3.
Maximum and minimum values of variables
| (T) (sec) | (I) (L/sec) | (T) (sec) | (I) (L/sec) | Correlation coefficient | |
| Minimum no. | 18.1 | 0.050 | 25.4 | 0.039 | -0.022 |
| Maximum no. | 137.5 | 0.130 | 226.3 | 0.094 | 0.820 |
정규화된 값을 바탕으로 K-means 알고리즘 적용하여 가구별 물 사용량을 분류하며 Elbow method를 적용하여 군집의 수를 결정한다.
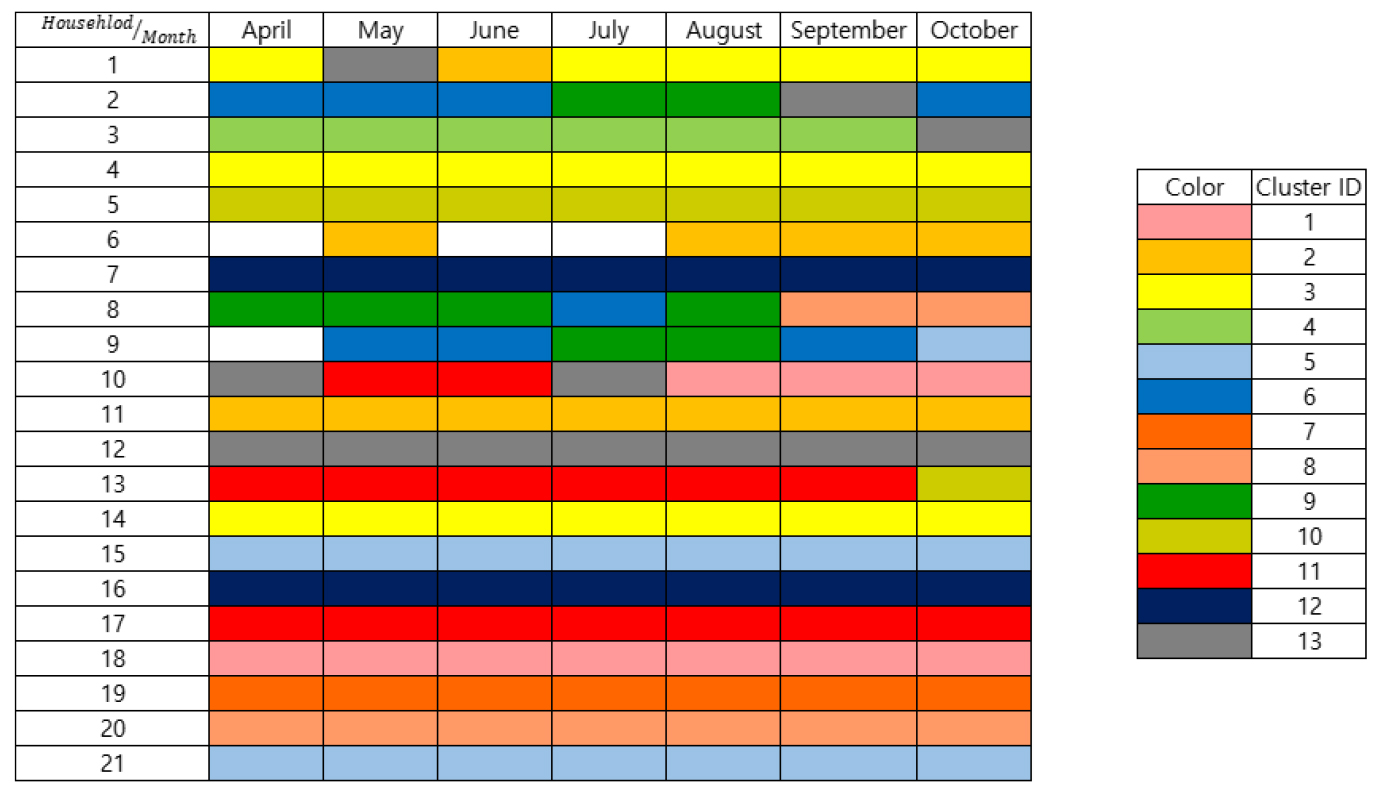
Fig. 6의 군집화 결과를 살펴보면 총 13개의 군집으로 기존의 21개의 가구보다는 적은 수로 분류가 된 것을 볼 수 있다. 또한, 특정한 가구의 경우는 같은 군집에 배치되는 것을 볼 수 있다. 예를 들어, 17번 가구의 경우 4월부터 10월까지의 모든 데이터가 11번 군집에 속하는 것을 확인할 수 있다. 몇몇 가구의 경우는 단일 가구의 월별 데이터가 여러 개의 군집으로 나뉘어져서 분류된 것을 볼 수도 있다. 여러 가구의 월별 데이터들이 한 개의 군집을 구성하는 경우, 일반적으로 2 ~ 3개의 가구가 하나의 군집을 구성한다. 예를 들어, 13번 군집의 경우는 한 개의 군집 안에 5개의 가구가 속하는 것을 볼 수 있다. 즉, 한 개의 가구 내에서도 월마다 다른 거동을 보여 다른 가구와 같은 군집으로 분류되는 가구가 있는가 하면 월별 거동이 거의 균일한 거동을 보여 같은 군집으로 분류(예를 들어, 가구 4번, 7번)된 것을 확인할 수 있었다. 각 경우에 대해서 아래에서 자세한 논의를 수행한다.
1개의 가구가 1개의 군집을 구성하는 경우에 속하는 군집 ID는 4, 7이다. ID 4는 3번 가구의 4월에서 9월까지의 데이터를 포함하고 있었으며 해당 데이터의 평균 물 사용 강도, 지속 시간의 표준편차, 상관계수가 해당 특징들의 범위 내에서 중간값을 가지는 것을 볼 수 있었다. 3번 가구의 10월 데이터는 3번 가구의 4월에서 9월까지의 데이터가 가지는 값들과 다른 값들을 보였고, 해당 값이 ID 13으로 분류된 가구들의 월별 데이터들과 비슷한 값을 보였다. 따라서 3번 가구의 10월 데이터를 제외한 나머지 월별 데이터들은 같은 군집으로 분류되었다고 볼 수 있다. ID 7은 19번 가구의 4월에서 10월까지의 전체 데이터가 포함되어 있으며, 특징적인 것은 평균 지속 시간과 지속 시간과 물 사용 강도의 상관계수가 최댓값 및 그에 가까운 값들로 구성되어 있었다는 것이다.
2개의 가구가 하나의 군집을 구성하는 경우의 군집 ID는 1, 8, 10, 12이다. ID 1, 8, 10의 경우는 2개의 가구 데이터가 해당 군집을 구성하는 비율이 균일하지 않고, 한 가구의 데이터 비율이 훨씬 높고 다른 가구의 데이터 비율이 낮았다. 특히, 데이터의 비율이 낮은 8번, 10번, 13번 가구의 경우 8, 9, 10월과 같이 늦여름과 가을의 데이터가 데이터의 비율이 높은 가구로 분류되는 것을 볼 수 있었다. ID 12의 경우는 7번과 16번 가구의 4월에서 10월까지의 전체 데이터가 같은 군집으로 분류되는 것을 볼 수 있었다. Fig. 6에서 7번과 16번 가구의 그래프 범위 및 분포가 비슷한 양상을 띠는 것을 확인할 수 있었다.
3개의 가구가 하나의 군집을 구성하는 경우의 군집 ID는 2, 3, 5, 6, 9, 11이다. 이 경우는 대체로 3개의 가구 데이터 중에서 1개 가구의 데이터 비는 매우 낮고 2개 가구의 데이터 비가 비슷하게 군집을 구성하는 양상을 보였다. ID가 3인 경우 1, 4, 14번 가구의 데이터가 포함되어 있는데 해당 가구들의 데이터 구성비가 거의 비슷한 것을 볼 수 있었다. 같은 군집을 구성하는 가구들이 해당 가구의 전체 월별 데이터를 포함하는 경우, 위의 지속 시간과 물 사용 강도의 그래프가 비슷한 형태와 범위를 갖는 것을 확인할 수 있었다.
5개의 가구가 하나의 군집을 구성하는 경우의 ID는 13이다. 13번 클러스터는 1, 2, 3, 10, 12번 가구의 데이터가 포함되어 있었고, 12번 가구의 모든 데이터가 포함되어 있고 1, 2, 3, 10번 가구의 데이터는 1 ~ 2개만 포함하고 있다. 해당 가구에 속하는 1, 2, 3, 10번 군집의 월별 데이터는 4, 5, 7, 8, 9, 10월 데이터로 겹치지 않는 것을 볼 수 있었다.
일반적으로, 최대-최소 정규화된 가구별 월별 데이터에 대해서 해당 데이터들이 유사한 값을 가지는 경우, 같은 ID를 가지는 군집으로 분류된다는 결과를 확인할 수 있었다. 한 가구 내에서 월별 데이터들이 뚜렷한 차이를 가지는 경우, 다른 가구의 데이터 중에서 해당 월 데이터와 비슷한 값을 가지는 가구와 함께 같은 군집으로 분류된다는 것을 확인할 수 있었다.
군집화 결과에서 흥미로운 것은, 3개 이상의 가구가 한 개의 군집을 구성하는 경우 한 가구 내에서 일부의 데이터들이 특정 군집으로 분류될 때, 분류되는 각 가구별 군집 내의 월이 대부분 겹치지 않는다는 것이었다. 예를 들어서, 2번 군집으로 분류되는 가구는 1, 6, 11번 가구인데 전체 데이터가 한 개의 군집으로 포함되는 11번 가구를 제외하고 6번과 11번 가구의 월별 데이터 중 2번 군집으로 분류되는 월별 데이터는 1번 가구는 6월, 6번 가구는 5, 8, 9, 10월로 월이 겹치지 않는 것을 볼 수 있었다.
4. 결 론
본 연구는 1997년 4월부터 10월까지 오하이오 주 밀포드의 21개 가구에 스마트미터를 설치하여 얻은 스마트미터 데이터의 활용방안을 제시하였다. 먼저 가구 수요량 스마트미터 데이터의 특성 및 활용법을 설명하고 K-means를 적용한 가구별 분류를 진행하였다. 스마트미터로부터 얻어진 스마트미터 데이터 셋은 크게 진입점과 사용점 데이터 셋으로 분류된다. 진입점 데이터 셋의 물 사용 패턴을 나타내는 것은 복합 직사각형 펄스이며, 사용점 데이터 셋은 단일 직사각형 펄스 형태를 보인다. 복합 직사각형 펄스로부터 단일 직사각형 펄스를 분리해내기 위해서 SMAPS 룰이 적용된다. 본 연구에서 진행한 K-means를 이용한 가구별 분류를 위해서 사용점 데이터 셋을 이용했다. 또한, 사용점 데이터 셋 중에서도 물 사용 강도와 지속 시간이라는 2가지의 특징을 선택하여 가구별 분류에 사용하였다. 일별 데이터를 K-means에 적용하기에는 데이터의 양이 방대하다는 문제점이 발생하였고 일별 데이터를 평균을 내어 월별 데이터로 변환하였다. 최종적으로 각 가구별 지속 시간의 평균 및 표준편차, 물 사용 강도의 평균 및 표준편차, 물 사용 강도와 지속 시간의 상관계수에 대한 4월부터 10월까지의 월별 데이터를 K-means에 적용할 변수로 선택하였다. 군집화 결과, 21개의 가구는 총 13개의 군집으로 분류되었다. 하나의 군집을 이루는 가구는 1개부터 5개의 가구로 나타났다. 또한, 하나의 군집을 구성하는 가구들의 개수에 따른 특징을 비교해보았고, 3개 이상 가구의 데이터들이 하나의 군집을 구성하는 경우, 월이 겹치지 않는 흥미로운 결과를 얻을 수 있었다.
본 연구는 스마트미터 데이터의 다양한 활용방안 중 한가지로써 비지도 기계학습법의 한 가지인 K-means를 활용한 가구별 분류를 진행하여 가구들을 분류해 보았다는데서 의의를 갖는다고 할 수 있다. 총 21개의 가구에 대한 데이터가 13개의 군집으로 분류되었고, 가구가 다르더라도 물 수요패턴에 따라서 동일한 군집으로 분류되는 결과를 통해서 물 수요패턴 분석의 중요성을 알 수 있었다.
본 연구는 해외의 데이터를 사용하여 분석을 진행해보았기 때문에 결과를 분석하는 과정에서 우리나라의 사용패턴과는 차이가 존재할 것이다. 우리나라의 스마트미터 데이터를 활용하여 분석을 진행하고 결과를 비교해보는 것도 흥미로운 연구가 될 수 있다. 각 가구별로 수요량 패턴에 분명한 차이가 있으므로, 국내에서의 가구별 물 수요를 분류해본다면 가구별 수요량 패턴을 통해 각 가구별 물 사용의 효율적인 방안을 찾는데 활용될 수 있을 것이다.
따라서 본 연구와 관련하여 향후에 진행할 수 있는 몇 가지 연구들이 있다. 본 연구에서는 복합 직사각형 펄스를 단일 직사각형 펄스로 변환하는 2가지의 SMAPS 룰을 제안하였다. 하지만 진입점 데이터 셋을 분석해본다면 2가지보다 더욱 많은 SMAPS 룰을 발견할 수 있을 것이다. 또한, 스마트미터 데이터의 가구별 분류에 다양한 방법론을 적용할 수도 있을 것이다. 본 연구에서는 가구별 군집화를 위해 K-means 알고리즘을 적용하였지만 그 외 다양한 기계학습법을 적용하여 결과를 비교분석하여 가구별 물 사용량 분류에 최적화된 방법론을 제안할 수 있다. 또한, K-means 알고리즘의 적용성을 검토하는 것 역시 흥미로운 주제이다. 본 연구에서는 5가지 변수를 사용하여 가구별 물 수요량을 분류하였지만 그 외 다른 정보(예: 부피 등)를 활용하여 결과를 분석할 수 있다. 더 나아가, 가구별 물 수요량이 아닌 사용점 데이터에 초점을 맞춘 결과 분석이 가능하다. 이는 가구별 물 수요량이 발생하였을 때 어느 사용점에서 측정된 것인지 파악하는데 도움을 줄 것이다.