1. 서 론

최근 기후변화로 인한 가뭄과 홍수 등의 이상 기후와 물 공급의 지역적 불균형으로 물 부족 현상의 발생 빈도가 증가하고 있다. 이에 따라 수자원의 안정적인 공급과 체계적인 관리의 중요성이 대두되고 있다(Yoon et al., 2016). 지하수는 생활용수, 공업용수, 농업용수 등 여러 용도로 활용할 수 있는 중요한 수자원으로, 이러한 문제에 대한 대안이 될 수 있다. 그러나 지하수의 무분별한 개발은 지하수 자원의 고갈, 오염 확산, 지반 침하, 해수 침투 등의 문제를 유발하여 인문 활동 및 생태계에 부정적인 영향을 미칠 수 있다(Choi, 2003; Lee et al., 2007). 지하수는 지하에 존재하기 때문에 관리가 어렵고, 오염되었을 경우 정화에 많은 시간과 비용이 소요된다. 따라서 지하수 자원의 최적 개발과 오염원 관리는 매우 중요한 문제이다(Kim, 2003).

지하수 모델은 복잡한 지하 세계인 실대수층의 상황을 단순화시켜 재현한 것으로, 지하수 자원의 최적 관리나 오염 지하수의 정화 등의 문제를 해결하는 데 매우 유용하다. 지하수 수치 모델은 편미분방정식을 기반으로 하며, 1800년대 후반부터 지하수 유동 및 용질 이동 연구에 사용되고 있다(Hahn and Hahn, 1999; Lee et al., 1999). 그중 미국지질조사소(U. S. Geological Survey, USGS)에 의해 고안된 MODFLOW (Modular Three-Dimensional Finite Difference Flow Model; McDonald and Harbaugh, 1988)는 3차원 유한차분법을 이용한 지하수 유동 모델로 전 세계적으로 널리 사용되고 있으며(Hahn, 1998; Kim, 2018), Visual MODFLOW, GMS 등의 상용 소프트웨어로 제공되고 있다(Jeong et al., 2016). 이러한 상용 소프트웨어는 그래픽 사용자 인터페이스(Graphical User Interface, GUI)로 모델을 만들 때, 일련의 버튼만 누르면 된다는 장점을 가지고 있다. 하지만 만든 모델을 쉽게 재생산, 복제, 또는 독립적으로 검증할 수 없으며, 모델링 오류 발생 시 수정하기 어렵다는 단점이 있다(Bakker, 2014). 이에 따라 스크립팅(Scripting) 형태의 MODFLOW 기반 파이썬(Python) 패키지인 FloPy가 개발되었다.

FloPy는 MODFLOW 모델을 개발, 실행 및 후처리하기 위한 파이썬 패키지(Bakker, 2014; Bakker et al., 2016)로 기존의 그래픽 사용자 인터페이스에서 구현되지 않은 패키지를 포함하여 모든 MODFLOW 기능을 지원하는 유연성으로 MODFLOW 구현을 용이하게 한다(Daoud et al., 2022). 하지만 FloPy를 실행하기 위해 FloPy 외에도 판다스(Pandas)와 넘파이(NumPy) 같은 파이썬 패키지가 필요하며, FloPy 설치 후에는 MODFLOW 및 MODFLOW 관련 파일을 추가로 설치해야 한다는 번거로움이 있다.

따라서 본 연구에서는 스크립트 작성에 이상적이고 무료 오픈 소스 프로그래밍 언어(Bakker, 2014)인 파이썬을 이용하여 MODFLOW 기반 모델이 아닌 독자적인 스크립팅 형태의 유한차분법 기반 정류 상태 지하수 유동 모델을 구축하였다. 이후, 제주도 유역에 적용하여 수두 분포를 파악하고, 관측 수두 및 MODFLOW로 계산된 수두와 비교하여 모델의 타당성을 검토하였다.

2. 연구방법

2.1 지하수 유동 방정식

일정한 밀도를 가지는 다공성 매질을 통해 흐르는 3차원 지하수 유동은 Eq. (1)과 같이 편미분 방정식으로 나타낼 수 있다.

여기서 Kxx,Kyy,Kzz는 x,y,z 방향에서의 수리전도도, h는 수두, W는 지하수의 유입 또는 유출량, Ss는 비저류계수, t는 시간이다. 시간의 흐름에 영향을 받지 않는 정류 상태일 경우, 오른쪽 항이 0이 되며, Eq. (2)로 표현할 수 있다.

편미분 방정식의 해석학적인 해는 구하기 매우 어렵다. 따라서 비교적 그 원리를 이해하기 쉽고, 현장에 적용하기 유용한 유한차분법(Craig and Rabideau, 2006; Park, 2007)을 이용한 수치해석으로 근삿값을 얻는다. 즉, 유한차분법으로 차분화하여 수두를 계산할 수 있다. 유한차분형식의 지하수 유동 방정식은 연속방정식을 이용하여 Eq. (3)으로 표현할 수 있다.

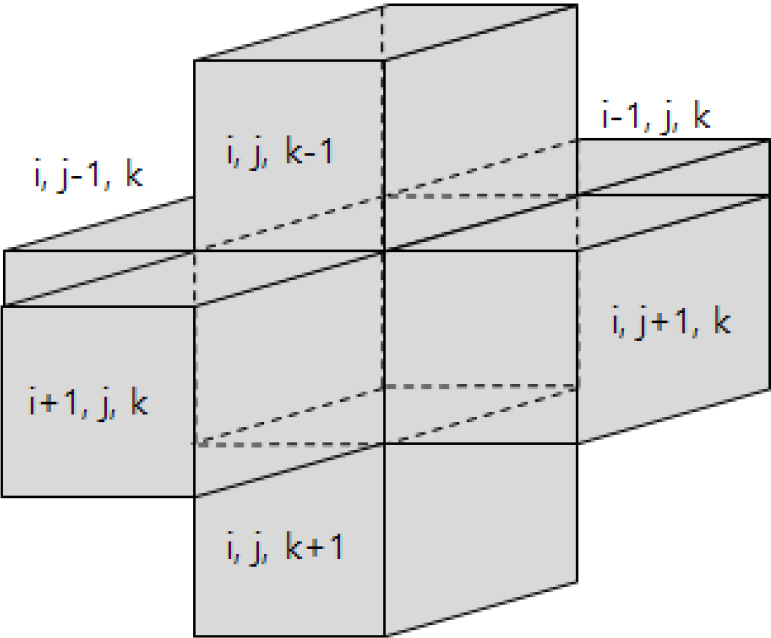
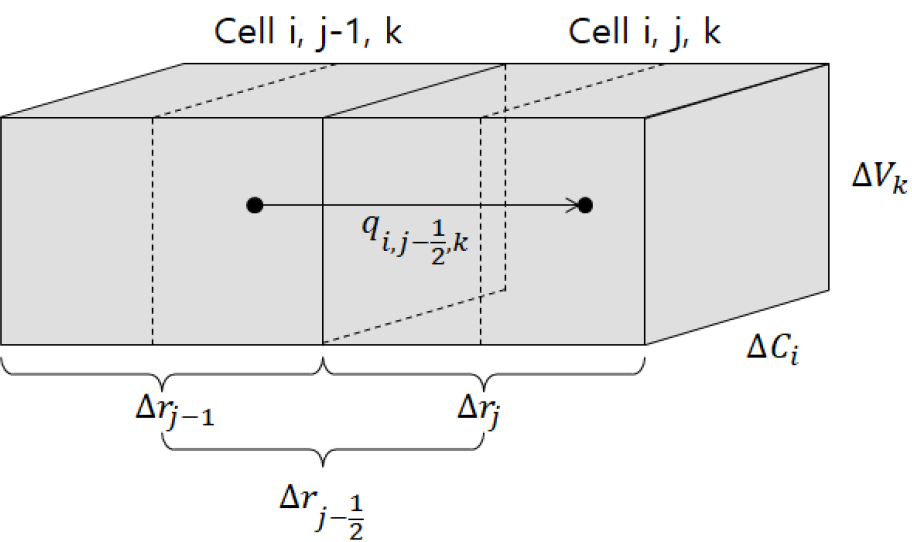
여기서 Qi는 지하수 유동량이다. Fig. 1은 (i, j, k) 셀 주위에 소재한 6개의 셀의 위치를 나타낸 그림이다. (i, j-1, k) 셀에서 (i, j, k) 셀로 유동하는 지하수의 유동량은 Darcy의 법칙을 이용하여 Eq. (4)로 나타낼 수 있으며, Fig. 2로 표현할 수 있다.

Fig. 1.

(i, j, k) cell and six adjacent cells

Fig. 2.

Groundwater flow from (i, j-1, k) cell to (i, j, k) cell

여기서 hi,j,k은 (i, j, k) 절점의 수두, hi,j-1,k는 (i, j-1, k) 절점의 수두, qi,j-12,k는 (i, j, k) 셀과 인접한 (i, j-1, k) 셀 사이의 지하수 유동량, KRi,j-12,k는 (i, j, k) 셀과 그 인접 (i, j-1, k) 셀 사이의 수리전도도로, 조화평균으로 구한 값, △Ci△Vk는 단면적, △rj-12는 절점 (i, j, k)와 인접 절점 (i, j-1, k) 사이의 거리이다. 격자망이 설정되면 단면적과 해당 셀의 수리전도도, 인접 격자 사이의 간격은 일정한 값을 가진다. 따라서 단면적과 수리전도도, 격자 사이의 간격을 곱한 값은 상수가 된다. 이를 전도계수(CRi,j-12,k)라 하고, Eq. (5)로 나타낼 수 있다.

Eq. (5)을 Eq. (4)에 대입하여 나타내면 Eq. (6)과 같다. 즉, (i, j, k) 셀로 유입·유출되는 지하수의 유동량은 인접 셀의 수두와 (i, j, k) 셀의 수두 사이의 차와 전도계수로 구할 수 있다.

이외 배수, 함양, 우물에서 지하수의 양수 등과 같이 대수층의 외부작용으로 인해 (i, j, k) 셀로 유동되는 유동량은 상기 식에다 간단히 이에 해당하는 외부작용항을 추가하면 되고, Eq. (7)로 나타낼 수 있다.

여기서 Pi,j,k은 수두에 따라 유동량이 변하는 상수, Qi,j,k는 수두와 독립적인 유동항이다. 외부작용으로 인한 유동량은 (i, j, k) 셀의 수두에 따라 변할 수도 있고, 수두와 전혀 연관성이 없는 독립일 수도 있다. 배수의 경우, 수두에 따라 영향을 받으며, 함양과 양수는 수두에 상관없이 독립적이다. 수두를 포함하고 있는 모든 항은 왼쪽에 배열하고, 수두와 관련 없는, 즉 독립적인 모든 항은 오른쪽에 배열하면 Eq. (8)과 같다.

유한차분 격자망의 격자마다 Eq. (8)과 같은 유한차분 방정식이 한 개씩 만들어지며, 따라서 전체 격자망의 개수와 같은 숫자의 유한차분 방정식이 있게 된다. 이 식들을 연립으로 풀어야 하며, 연립방정식을 행렬식으로 표현하면 Eq. (9)와 같다.

여기서 [A]는 수두관련 상수 행렬, {h}는 수두 벡터, {q}는 상수항 벡터이다. 본 연구에서는 이러한 원리를 기반으로 파이썬을 이용하여 정류 상태 유한차분 지하수 유동 모델을 구축하고, FDM 파이썬 모델(FDM Python Model)로 명명하였다.

2.2 FDM 파이썬 모델

모델 구축에 사용된 파이썬 패키지는 판다스, 넘파이, 사이파이(SciPy)이다. 판다스는 표 형태의 자료를 다루기 위한 패키지, 넘파이는 행렬연산 등 수치해석과 관련된 기능을 구현할 때 가장 기본이 되는 패키지, 사이파이는 미분 방정식 계산 등에 사용되는 패키지이다. 고도, 초기수두 등 csv 형태의 입력 자료를 읽고, 계산된 수두를 저장하기 위해 판다스, 셀의 두께, 배수되는 양 등 행렬연산을 위해 넘파이, 수두 계산 시 시간 단축을 위한 희소행렬 생성과 행렬식 계산을 위해 사이파이를 사용하였다.

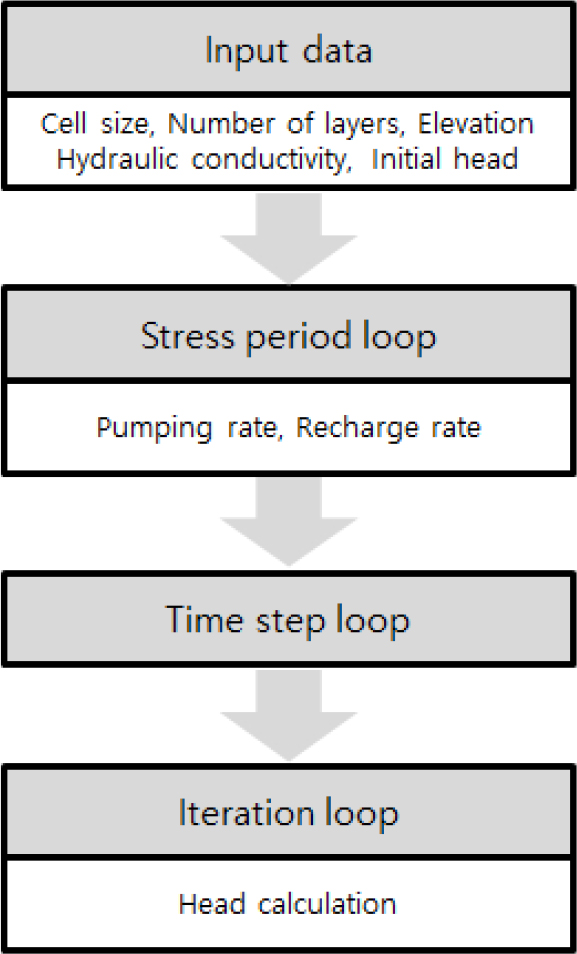
MODFLOW와 비슷하게 입력 자료를 읽는 단계, 스트레스 기간 루프(Stress period loop), 시간 단계 루프(Time step loop), 반복 루프(Iteration loop)로 구성하였다(Fig. 3). 스트레스 기간 루프를 실행하기 전 단위격자의 크기, 대수층의 개수, 고도, 수리전도도, 초기수두 등 입력 자료를 읽는다. 스트레스 기간 루프에서는 양수량, 함양량, 배수되는 양 등 대수층의 외부 작용과 관련된 자료를 읽거나 계산한다. 스트레스 기간 동안 양수량, 함양량, 배수되는 양은 변하지 않는다. 스트레스 기간은 여러 시간 단계로 구성될 수 있으며, 각 시간 단계 말에 수두가 계산된다. 반복 루프에서는 행렬식을 이용하여 수두를 계산하며, 반복연산법 중 지하수 문제에 가장 널리 이용되고 있는 Successive Over Relaxation (SOR)을 사용하였다. 이전 반복으로 계산된 수두와 현재 계산된 수두의 차가 허용한계(Tolerance)에 가까워질 때까지 반복하여 수두를 계산한다. 즉, 수두가 수렴할 때까지 반복한 후, 수렴된 수두를 결과 수두로 출력한다.

Fig. 3.

Flowchart of FDM Python Model

3. 적용 및 분석

3.1 개념모델 설정

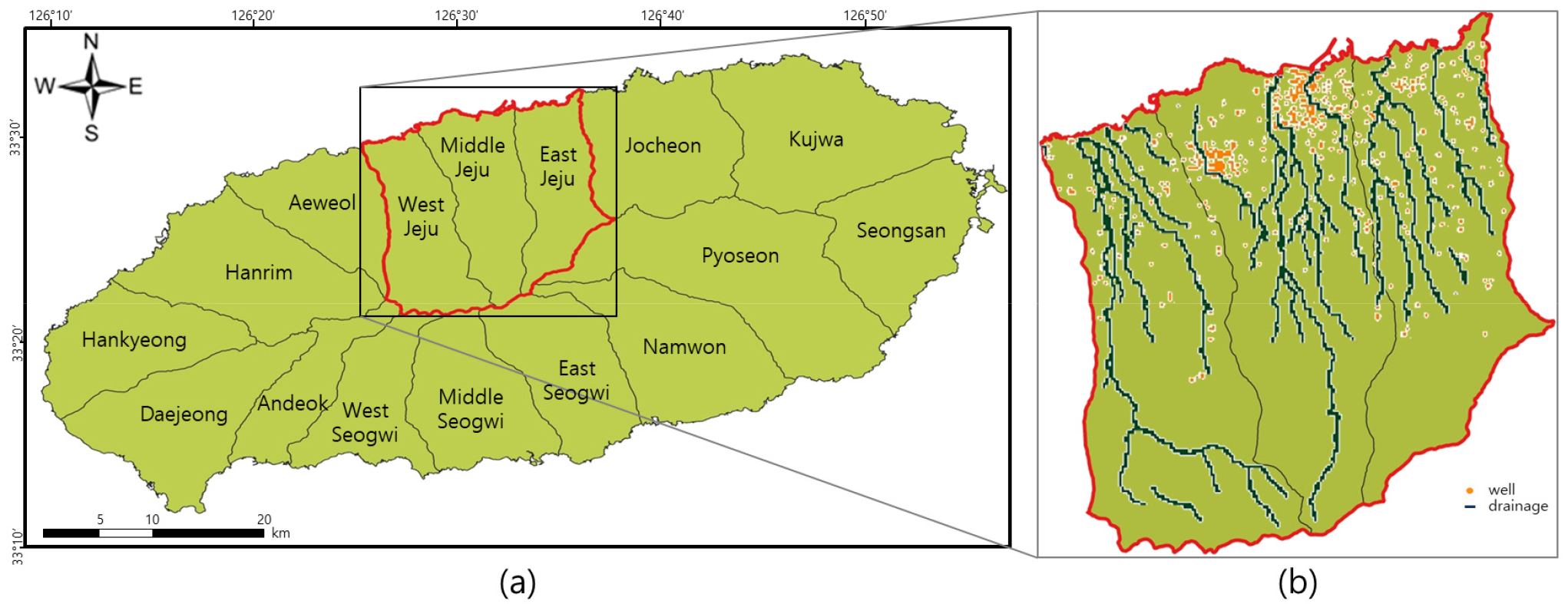
개념모델은 지하수계의 공간적 형태 및 지하수계에서 발생하는 복잡한 흐름 특성을 단순하게 표현하는 것으로 모델링할 때 기초적이면서 가장 중요한 단계이다. 모델링 연구 대상 유역은 제주도의 중제주, 동제주, 서제주로 설정하였다(Fig. 4). 모델 영역의 면적은 약 250 km²로, 유역면적 및 모사에 따르는 전산코드 수행시간을 고려하여 전체 격자 크기는 202 행 × 192 열, 단위격자 크기는 100 m × 100 m로 설정하였다.

Fig. 4.

Maps showing (a) the study area in Jeju Island and (b) the location wells (yellow dot) and drainage (blue line)

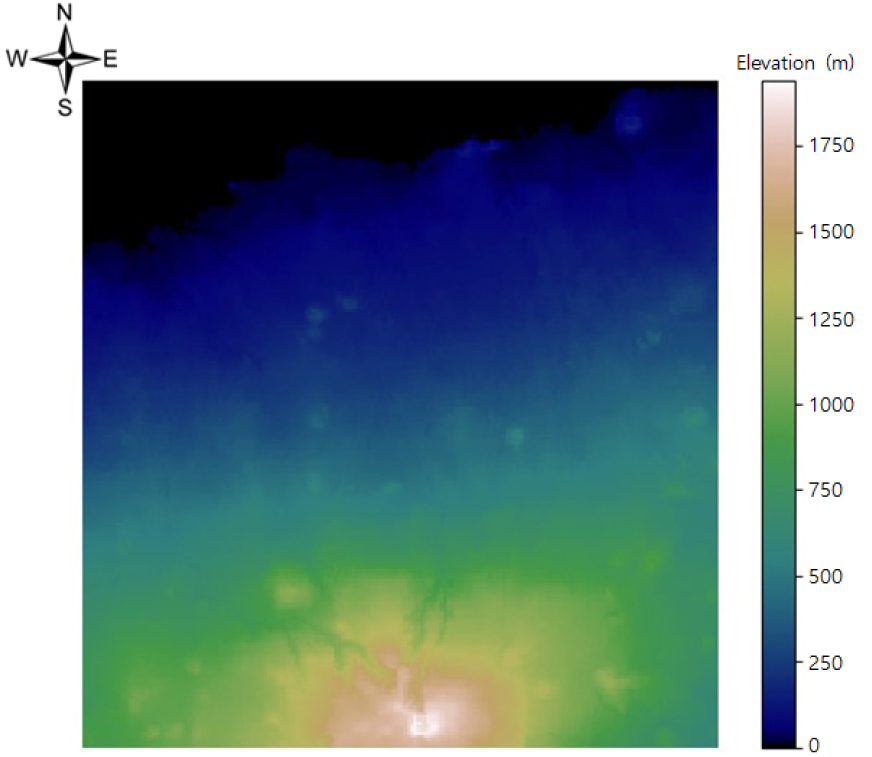
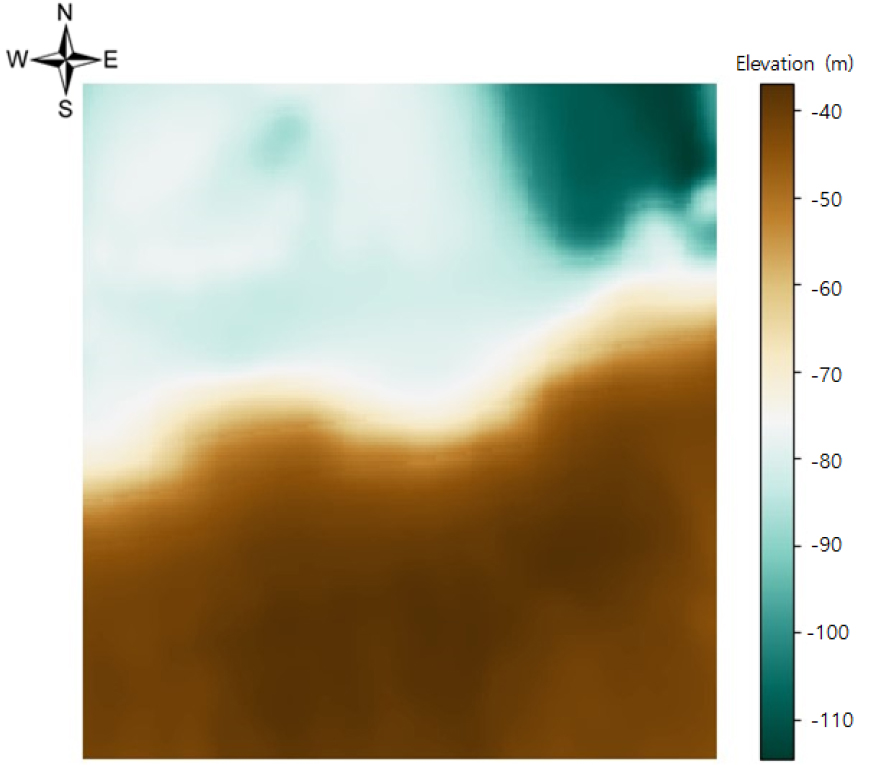
제주도의 지질구조는 불투수층 또는 저투수층으로 알려진 U층 위에 응회암층, 퇴적암층, 현무암층으로 이루어져 있으므로(KIGAM, 2008), 하나의 자유면대수층으로 가정하였다. 이에 따라 모델의 상부는 수치표고모델(Digital Elevation Model, DEM)에 의한 지표면으로 설정하고(Fig. 5), 최하부는 U층의 분포를 따르도록 설정하였다(Fig. 6). 개념모델 설정에 사용된 자료의 목록과 제공 기관을 표로 정리하였다(Table 1). 수치표고모델은 국토정보플랫폼에서 제공하는 국토지리정보원 출처의 1:5,000 수치지형도(388개 도엽)에서 수집한 고도 자료를 이용하여 불규칙삼각망분석(Triangulated Irregular Network, TIN)을 수행한 후 연구지역과 같이 100 m × 100 m 단위격자 크기로 구축하였다. U층의 분포는 한국지질자원연구원 보고서(KIGAM, 2008)의 U층 자료에 크리깅(Co-Kriging) 기법을 적용하여 보간하고 모델링 영역으로 추출하였다.

Fig. 5.

Digital Elevation Model (DEM) data of study area

Fig. 6.

U-Formation layer depth

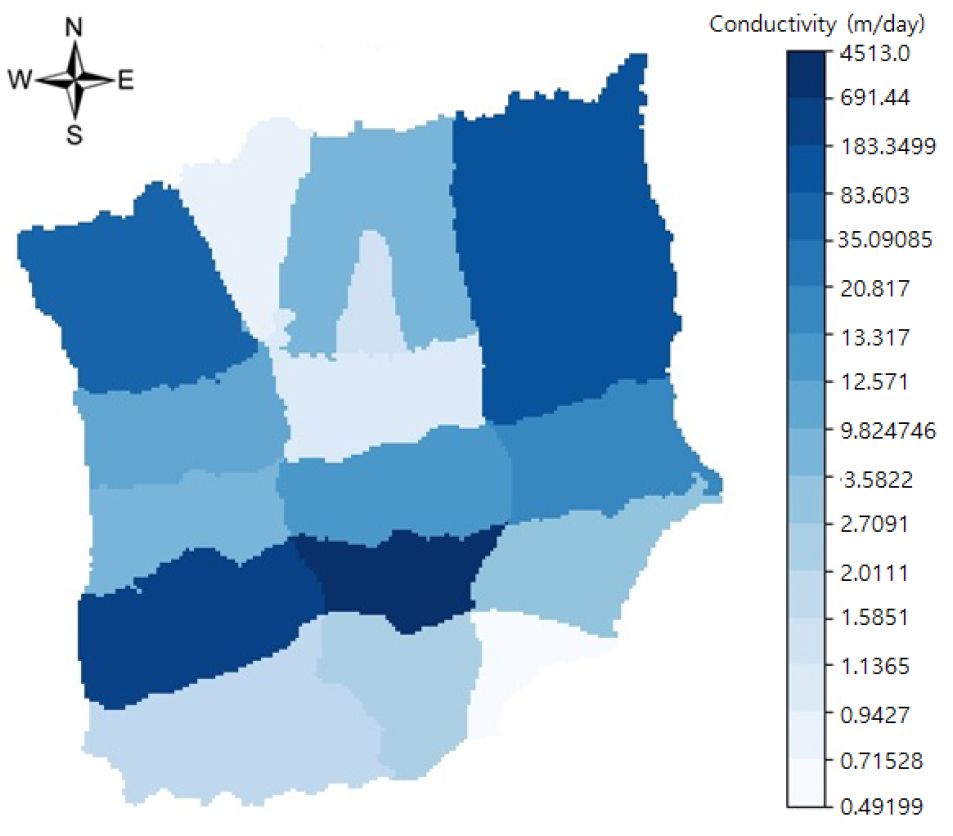
대상 유역의 북쪽 경계는 해수면과 접하고 있어 유입 및 유출량에 관계없이 수두를 유지하는 일정수두경계로 설정하였다. 수리전도도는 지하수영향조사 보고서에 수록된 이용관정의 수리전도도를 각각 평균하여 적용하였다(Fig. 7).

Fig. 7.

Distribution of hydraulic conductivity

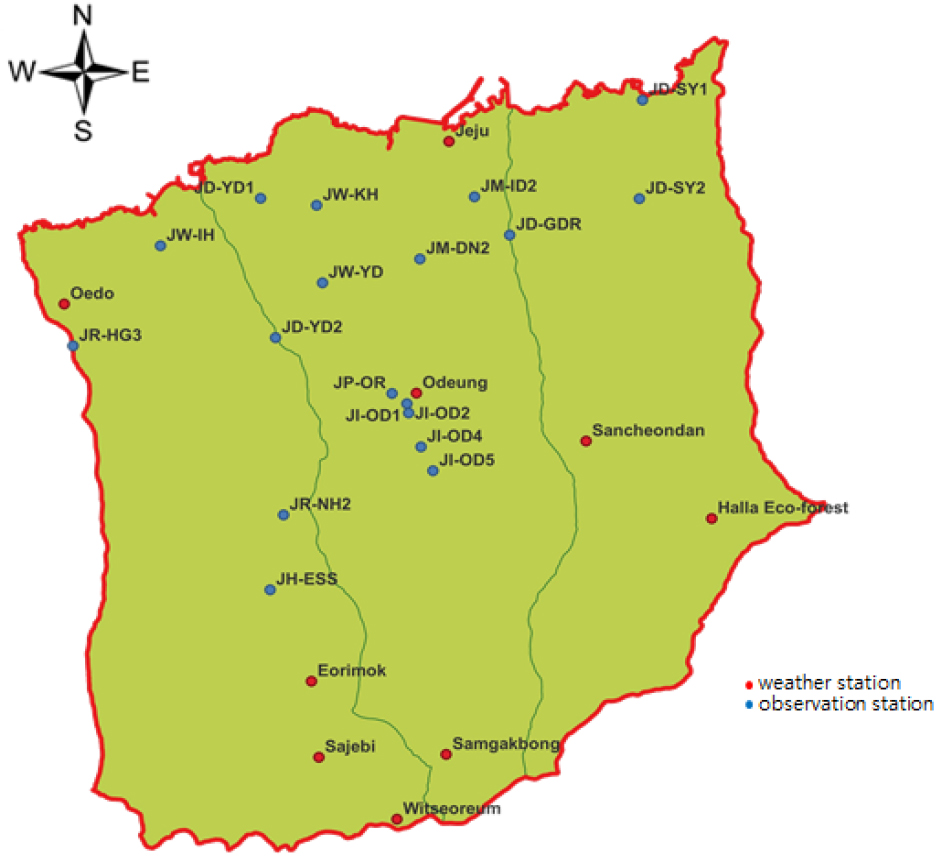
지하수위, 이용량, 강수량 등은 제주도에서 운영 중인 기상 및 지하수 관측소의 관측 자료를 이용하였다. 제주도의 하천은 대부분 우기에만 흐름이 생기는 건천이므로 하천에서 지하수계로 물의 공급은 없고 오직 지하수계에서 하천으로 배출만 일어나는 것으로 가정하여 배수 경계로 설정하였다. 용천수도 하천과 동일한 기작으로 발생하는 것으로 가정하였다(Fig. 4(b)). 모델링 영역 내 존재하는 제주도 용천수 관정(152공), 수치지형도의 하천경계 자료의 DEM으로부터 위치와 고도 값을 추출하였다. 배수 전도계수(Cd)는 제주도 지하 매질의 일반적인 투수 특성을 고려하여 배수가 원활하게 이루어지는 것을 가정하여 큰 값(100 m²/d)을 일괄적용하고 보정을 통해 지역적으로 조정하였다. Eq. (10)과 같이 대수층에서 배수되는 양(Qd)은 대수층의 수두(h)와 배수 고도(d) 차이에 비례한다. 계산 수두가 배수 고도보다 작으면 배수가 되지 않는다.

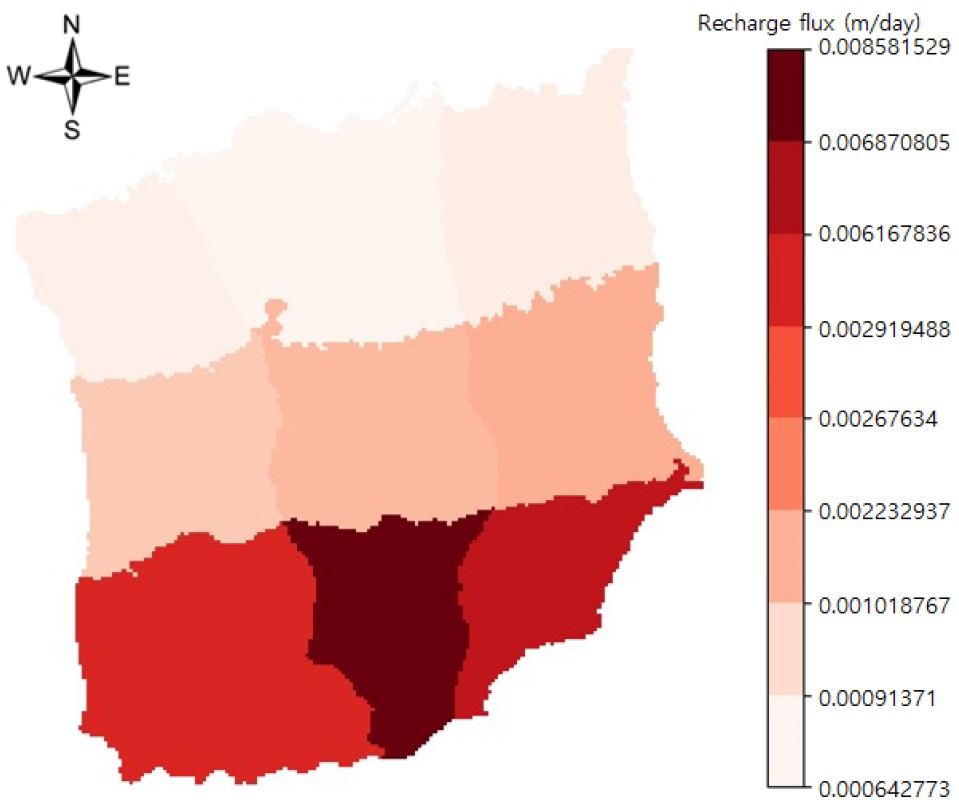
양수에 의한 지하수 분포 변화를 반영하기 위해 제주도 지하수 이용량 측정관정 570개소의 지하수 이용량 측정값을 사용하였다(Fig. 4(b)). 선 수행된 연구(Park et al., 2014)에서 제주도의 수계별 고도별 분포형 함양량이 계산된 바 있으며, 이를 인용하여 함양률을 산출하고 제주도 기상 관측소(총 9개소, Fig. 8)의 월별 10년(2011~2020년) 평균 강수량을 반영하여 함양량을 생성하였다(Fig. 9).

Fig. 8.

Map showing the location weather stations (red dot) and observation stations (blue dot)

Fig. 9.

Distribution of recharge flux

3.2 모사 결과

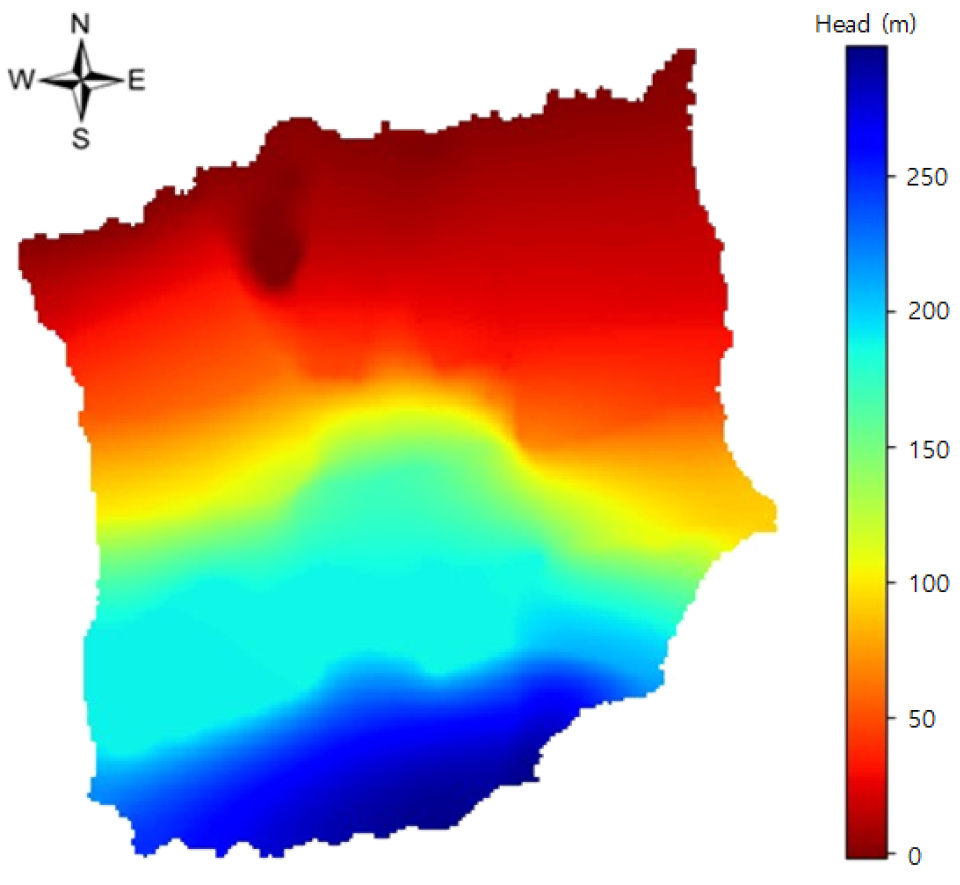
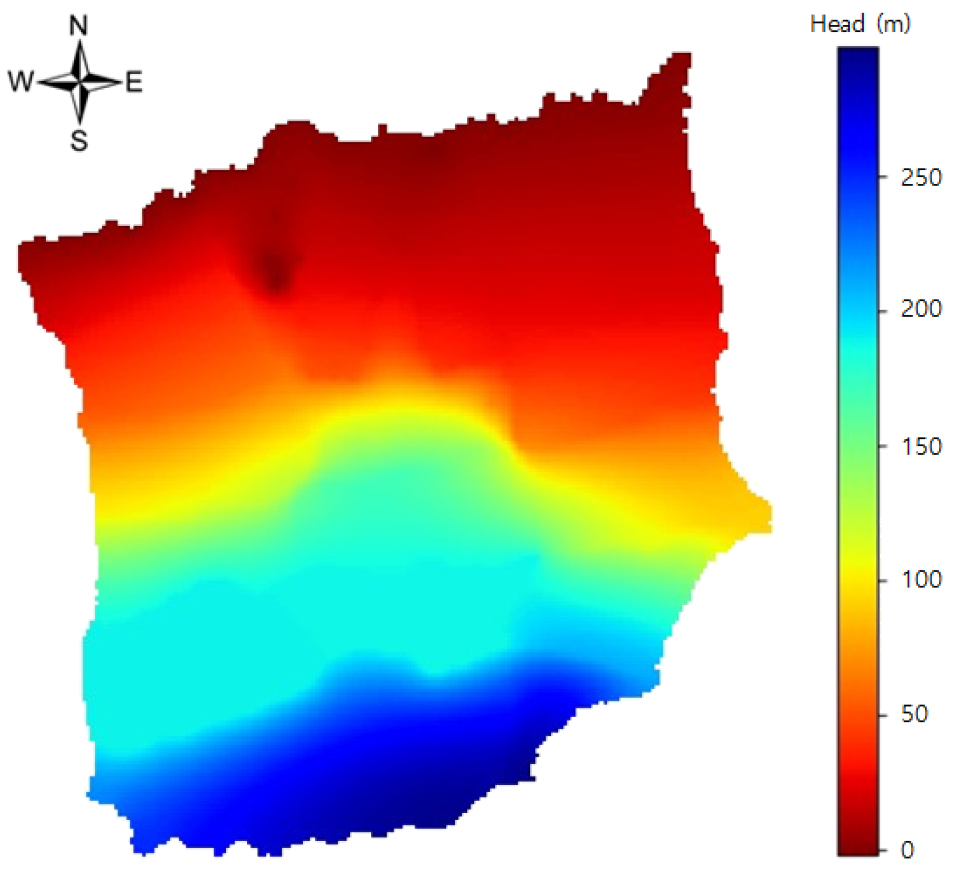
연구 지역의 지하수 해석을 위하여 MODFLOW와 본 연구에서 개발한 FDM 파이썬 모델을 이용하였으며, 모델의 타당성은 관측 수두와 비교하여 검토하였다. MODFLOW로 계산된 수두의 최솟값은 -20.36 m, 평균값은 110.59 m, 최댓값은 295.62 m이며, 그 분포는 Fig. 10과 같다. FDM 파이썬 모델로 계산된 수두의 최솟값은 -4.90 m, 평균값은 111.37 m, 최댓값은 295.93 m이며, 그 분포는 Fig. 11와 같다. 관측 수두는 제주도 지하수위 관측망 자료에서 지하수 관측소(총 18개소, Fig. 8) 수두의 월별 평균값과 10년(2011~2020년) 평균값을 사용하였다(Table 2). 지하수 관측소 위치에 해당하는 MODFLOW와 FDM 파이썬 모델의 수두값은 Table 3과 같다.

Fig. 10.

Groundwater heads under steady-state condition from MODFLOW

Fig. 11.

Groundwater heads under steady-state condition from FDM Python Model

관측 수두와 계산된 수두의 결정계수(R2)를 계산하여 표로 나타내었다(Table 4). FDM 파이썬 모델로 계산된 수두와 관측 수두가 MODFLOW로 계산된 수두보다 유사한 것을 확인할 수 있다. 특히 관측 수두의 10년 평균값과 MOD FLOW의 결정계수는 0.9427, FDM Python 모델의 결정계수는 0.9429이다. 본 유역에 대한 지하수 유동 해석에 있어 정류 상태에 따른 MODFLOW와 FDM 파이썬 모델의 계산된 수두의 결정계수는 0.9997이다.

4. 결 론

본 연구에서는 오픈 소스 프로그래밍 언어인 파이썬을 이용하여 스크립팅 형태의 유한차분법 기반 정류 상태 지하수 유동 모델을 구축하고, FDM 파이썬 모델로 명명하였다. FDM 파이썬 모델에 대한 현장 적용성을 검토하기 위해 제주도의 중제주, 동제주, 서제주 유역을 대상으로 지하수 흐름 모사를 수행하였다. 모델의 타당성은 관측 수두 및 MODFLOW로 계산된 수두와 비교하여 검토하였다.

MODFLOW 기반 모델이 아닌 독자적인 스크립팅 형태의 지하수 유동 모델의 구축으로 모델을 쉽게 재생산, 복제 또는 독립적으로 검증할 수 있으며, 모델링 오류 발생 시 수정이 가능하게 하였다. 또한, 원리를 이해하기 쉽고, 현장에 적용하기 용이한 유한차분법을 이용하여 지하수 유동 방정식을 간단한 행렬식으로 나타내고, 행렬식을 통해 수두를 계산하였다. 파이썬 패키지 중 판다스, 넘파이, 사이파이를 사용하여 모델을 구축하였으며, MODFLOW와 비슷하게 입력 자료를 읽는 단계, 스트레스 기간 루프, 시간 단계 루프, 반복 루프로 구성하였다.

모델링 연구 대상 유역을 하나의 자유면 대수층으로 가정하여 상부는 수치표고모델에 의한 지표면, 하부는 U층의 분포를 따르도록 하였다. 해수면과 접하고 있는 북쪽은 일정수두경계, 하천과 용천수는 배수 경계, 함양량과 양수량 등을 경계 조건으로 설정하였다. 수리전도도는 지하수영향조사 보고서에 수록된 이용 관정의 수리전도도를 각각 평균하여 적용하였다. 이러한 개념모델을 바탕으로 MODFLOW 및 FDM 파이썬 모델을 이용하여 정류 상태 모사를 수행하였다.

모사 결과를 10년 평균 관측 수두와 비교 시 FDM 파이썬 모델로 계산된 수두와의 결정계수는 0.9429, MODFLOW로 계산된 수두와의 결정계수는 0.9427로 FDM 파이썬 모델로 계산된 수두가 좀 더 높은 유사성을 보였다. 또한, MODFLOW와 FDM 파이썬 모델로 계산된 수두의 결정계수는 0.9997이다.

FDM 파이썬 모델로 계산된 수두가 관측 수두 및 MOD FLOW로 계산된 수두와 높은 유사성을 보이며, 이를 통해 기존 MODFLOW 기반의 상용 소프트웨어나 파이썬 패키지가 아닌 독자적인 정류 상태 지하수 유동 모델로 활용할 수 있을 것으로 보인다. 추후 시간의 흐름을 고려한 부정류 상태 모델을 구축하고, 웹 기반 시스템에서 구현하여 지하수 자원의 최적 개발과 오염원 관리에 도움이 될 것으로 기대된다.