Evaluation of extreme rainfall estimation obtained from NSRP model based on the objective function with statistical third moment

Hemie Cho; Yong-Tak Kim; Jae-Ung Yu; Hyun-Han Kwon

doi:10.3741/JKWRA.2022.55.7.545

Preview

Research Article

Journal of Korea Water Resources Association. 31 July 2022. 545-556
https://doi.org/10.3741/JKWRA.2022.55.7.545

Evaluation of extreme rainfall estimation obtained from NSRP model based on the objective function with statistical third moment

통계적 3차 모멘트 기반의 목적함수를 이용한 NSRP 모형의 극치강우 재현능력 평가

Hemie Cho^a

Yong-Tak Kim^b

Jae-Ung Yu^c

Hyun-Han Kwon^d^*

조 혜미^a

김 용탁^b

유 재웅^c

권 현한^d^*

^aMaster Student, Department of Civil and Environmental Engineering, Sejong University, Seoul, Korea

^bPost-doctoral Associate, Department of Civil and Environmental Engineering, Hong Kong University of Science and Technology, Hong Kong

^cPh.D Student, Department of Civil and Environmental Engineering, Sejong University, Seoul, Korea

^dProfessor, Department of Civil & Environmental Engineering, Sejong University, Seoul, Korea

^a세종대학교 건설환경공학과 석사과정

^b홍콩과기대 건설환경공학과 박사후연구원

^c세종대학교 건설환경공학과 박사과정

^d세종대학교 건설환경공학과 교수

^{*Corresponding Author}

ABSTRACT

It is recommended to use long-term hydrometeorological data for more than the service life of the hydraulic structures and water resource planning. For the purpose of expanding rainfall data, stochastic simulation models, such as Modified Bartlett-Lewis Rectangular Pulse (BLRP) and Neyman-Scott Rectangular Pulse (NSRP) models, have been widely used. The optimal parameters of the model can be estimated by repeatedly comparing the statistical moments defined through a combination of parameters of the probability distribution in the optimization context. However, parameter estimation using relatively small observed rainfall statistics corresponds to an ill-posed problem, leading to an increase in uncertainty in the parameter estimation process. In addition, as shown in previous studies, extreme values are underestimated because objective functions are typically defined by the first and second statistical moments (i.e., mean and variance). In this regard, this study estimated the parameters of the NSRP model using the objective function with the third moment and compared it with the existing approach based on the first and second moments in terms of estimation of extreme rainfall. It was found that the first and second moments did not show a significant difference depending on whether or not the skewness was considered in the objective function. However, the proposed model showed significantly improved performance in terms of estimation of design rainfalls.

Keywords

NSRP

Extreme rainfall

Objective function

Stochastic precipitation model

Poisson process

수공구조물 설계 및 수자원 계획에서는 목표연도 이상의 수문기상자료를 활용하는 것이 추천된다. 강우 자료의 확장을 위해 추계학적 강수 모의 모형을 활용하는데, Bartlett-Lewis Rectangular Pulse Modified Model (BLRPM)과 Neyman-Scott Rectangular Pulse Model(NSRPM)이 대표적이다. 이 모형들은 확률분포의 매개변수 조합을 통해 추정되는 통계적 모멘트와 관측값의 통계적 모멘트를 반복 비교하여 최적 매개변수를 추정한다. 그러나 상대적으로 적은 관측값을 이용하여 매개변수를 추정하는 것은 부적절하게 정의된 문제(ill-posed problem)에 해당하며, 최적화 과정에서 매개변수 추정이 어려울 뿐만 아니라, 매개변수의 변동성도 매우 크다. 또한, 일부 연구에서 드러나듯이, 모형 매개변수 추정과정에서 다양한 목적함수를 활용해도 2차 모멘트에 국한되어 있어, 극치 강수량 재현에는 한계가 있다. 따라서 본 연구는 3차 모멘트를 포함한 목적함수를 활용하여 NSRPM 매개변수를 추정하고, 기존 2차 모멘트를 이용한 매개변수 접근방법과 극치강수량 재현 측면에서 비교를 수행하였다. 그 결과, 목적함수의 왜곡도 포함 여부에 따라 1, 2차 모멘트는 큰 차이를 나타내지 않았지만, 극치강우 재현 측면에서는 왜곡도를 포함한 경우가 포함하지 않은 경우보다 개선된 결과를 나타냈다.

키워드

NSRP 모형

극치강우

목적함수

추계학적 강수모형

포아송 과정

MAIN

1. 서 론
2. 분석자료
3. 연구방법
3.1 추계학적 강우 생성 모형과 포아송 클러스터 강우 생성 모형
3.2 BLRP 모형과 NSRP 모형
4. 연구결과
5. 결 론

1. 서 론

수공구조물 설계 및 수자원 계획에서는 목표연도 이상의 수문기상자료를 활용하는 것이 추천된다. 예를 들어, 댐의 용수공급계획을 수립하는 경우 운영 기간을 넘어서는 자료를 이용하는 것이 댐의 용수공급계획 측면에서 신뢰성을 기할 수 있다. 기후변화 등으로 인해 강수의 변동성이 커지고 있으며, 이러한 시공간적인 변동성을 충분하게 고려할 만큼의 장기간 수문기상자료를 연속적으로 확보하는 것은 여전히 어려운 현실이다. 특히 우리나라의 경우, 강우 관측 초기 일 단위 이하(sub-daily)의 자료가 상대적으로 부족하기 때문에, 시간 단위 강수 자료는 분석 시 어려움이 있다. 이런 경우, 추계학적으로 강우를 모의하는 방안을 고려할 수 있으나, 일단위 이하의 강우자료는 변동성이 매우 크기 때문에 일강수량 모의에 비해 통계치를 복원하는 것이 쉽지 않다. 특히 시간 단위 강수량의 모의와 이를 통해 얻을 수 있는 다양한 지속시간(3, 6, 9, 12, 24시간 등)에 대한 강수량의 통계적 특성 또한 재현해야하므로 최적화 측면에서도 어려움이 따른다.

강우 자료를 확장하기 위한 목적으로 추계학적 강수 모의 모형을 활용하는데, 대표적으로 Modified Bartlett-Lewis Rectangular Pulse (MBLRP) 모형과 Neyman-Scott Rectangular Pulse (NSRP) 모형으로 구분된다. 추계학적 강수 모형으로 강우 모의 시, 관측강수량의 통계적 모멘트를 재현할 수 있도록 모형 매개변수를 최적화하는 과정이 필수적으로 요구된다. 우리나라와 같이 강우 변동성이 큰 경우, 매개변수의 민감도가 커서 매개변수를 추정하는 데 어려움이 있다(Verhoest et al., 1997).

기본적으로 모형 매개변수들의 조합을 통해 추정되는 통계적 모멘트와 관측값의 통계적 모멘트를 반복적으로 비교하면서 최적 매개변수를 추정하게 된다. 그러나 상대적으로 적은 관측값을 이용하여 매개변수를 추정하는 것은 부적절하게 정의된 문제(ill-posed problem)에 해당되며, 최적화 과정에서 매개변수 추정이 어려울 뿐만 아니라, 매개변수의 변동성도 매우 크다. 또한, 모형 매개변수 추정과정에서 다양한 목적함수가 활용되고 있으나, 고려되는 통계적 모멘트가 평균 및 분산 등 2차 모멘트에 제한되어 있어, 극치 강수량에 대한 재현성은 상대적으로 부족한 편이다. 일부 연구에서도 이러한 점이 드러났는데, 왜곡도(skewness)의 과소 추정으로 인해 극치 강수량을 추출했을 때 시간단위 강수량에서 특히 과소 추정이 크게 나타났다.

국내에서 Rectangular Pulse 모형을 이용한 시간 강우 모의 연구가 활발하게 진행되지만, 연구 대상의 기간이 강우가 집중되는 여름철에 국한되어 있는 경우가 많아 극치강수량이 과소 추정되는 문제가 존재한다. Kim et al. (2000)은 7월에 대해서만 4년의 시간단위 강우자료를 활용하여 NSRP 모형을 구축하고 강우 재현 능력을 평가하였다. 모의 발생한 다차원 강우자료가 비교적 실제자료의 일차원 강우모형을 잘 재현해내는 결과를 보였지만, 상당히 짧은 자료 연한으로 인해 자료 확장 시에도 재현력에 대한 신뢰를 유지할 수 있을지 우려된다. Kim et al. (2013)은 7월에 대해서 20년 이상의 시간단위 강우자료를 활용하여 BLRP 모형을 지역화하는 연구를 수행하였지만, 확률강우량 산정에 중요한 요소로 작용하는 극한강우 분포의 왜도를 고려하지 못하는 모형 특성으로 인하여 모형 기반 확률홍수량 산정값이 관측치 기반 산정값 대비 약 20~45% 작게 과소산정되었다. Lee and Kim (2016)은 6~9월에 대하여 39년간의 시간단위 강수량자료를 활용하여 NSRP 모형의 매개변수를 Bayesian 추론을 통해 추정하였다. 마코프 체인 몬테카를로(Markov chain Monte Carlo, MCMC) 알고리즘을 이용해 NSRP 모형의 매개변수의 사후 평균값들을 이용하여 누적강우의 2차 성질인 평균과 분산값을 잘 추정했지만, 2차 모멘트에 제한되었다는 한계가 있다. 따라서 홍수기만을 대상으로 하여 왜곡도가 과소 추정됨에 따라 극치 강수량이 과소 추정되는 것을 방지하는 것을 목표로 본 연구를 수행하였다. 홍수기에 제한되지 않고 열두 달 전체에 대하여 40년 이상의 기간을 대상으로 3차 모멘트까지 고려한 강우모의시계열을 생성하고, 이를 유역 단위로 확장 가능한 다지점 NSRP 모형으로 발전시켰다. 즉, 3차 모멘트인 왜곡도가 극치 강우를 재현하는 데 도움이 될 것으로 판단하여, 목적함수에 왜곡도를 포함하여 NSRP 모형의 매개변수를 추정하고, 기존 2차 모멘트를 이용한 매개변수 접근방법과 극치 강수량 재현 측면에서 비교를 수행하였다. 단일지점 NSRP 모형으로 극치 강수량 재현을 수행하고, 극치 강수량 재현을 유역 단위로 확대하기 위해 단일지점 NSRP 모형을 다지점 NSRP 모형으로 발전시켰다. 단일지점에 적용하는 NSRP 모형에 지점 간의 상관성을 복원하기 위해 순위상관계수(rank correlation)를 고려하였고, 관측값과 모의값에 대하여 공간 상관성을 비교하여 다지점 NSRP 모형의 모의 강우시계열 생성 능력을 평가하였다.

2. 분석자료

일단위 이하(sub-daily)의 강우시계열을 활용하는 NSRP 모형의 특성상, 본 연구에서는 시단위 강우자료를 사용하였다. 기상청 산하 종관기상관측소(automated synoptic observing system, ASOS) 102개소 중 40년 이상의 장기 기록을 보유한 관측소 56개를 선별하여 활용하였다. 선정한 56개 관측소의 1973년부터 2020년까지 48년의 자료를 기반으로 하여, 3차 모멘트인 왜곡도를 목적함수에 포함한 여부에 따라 NSRP 모형의 극치강우 재현 능력을 비교하였다. Fig. 1은 선별한 ASOS 관측소 56개소(청색)를 보여준다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F1.jpg

Fig. 1.

ASOS Weather stations over South Korea

3. 연구방법

3.1 추계학적 강우 생성 모형과 포아송 클러스터 강우 생성 모형

강우 자료의 한계를 개선하기 위한 목적으로 활용하는 추계학적 강수모의 모형으로는 포아송 클러스터(Poisson cluster) 계열의 강우 생성 모형을 주로 활용하는데, 특히 일 단위 이하 시간 규모의 강우시계열 생성을 위해 국내외에서 널리 활용한다(Kim, 2018). 포아송 클러스터 강우 생성 모형은 가상의 강우자료를 생성하여 제공함으로써 수자원 계획 시 강우 자료 부족으로 인한 샘플링 오차를 개선하는 데 도움을 준다. 포아송 클러스터 강우생성모형은 강우의 발생과정과 강우장의 강우 세포들이 분포되는 과정을 포아송 분포를 따르는 확률과정을 통하여 강우의 군집특성을 모의하는 모형이다. 추계학적 강우모의에서 중요한 점은 과거 강수 자료의 통계적 특성(평균, 분산, 자기상관계수, 왜곡도 등)을 다각적으로 재현하는 것이다(Boughton and Droop, 2003; So et al., 2015; Kim et al., 2016). 포아송 클러스터 강우 모형을 통해 생성된 가상의 강우량 자료가 다른 기후를 나타내는 여러 지역에서 관측 강우의 평균, 분산, 자기상관계수, 무강우확률 등 주요 통계치를 잘 재현해냄을 선행 연구에서 확인할 수 있다(Cowpertwait et al., 1996; Verhoest et al., 1997). 포아송 클러스터 강우생성모형은 지점 모형으로 5~6개의 비교적 적은 매개변수들로 시간 단위의 강우 시계열을 모의하는 장점이 있다. 강우모의를 위한 구형 펄스(Rectangular Pulse) 모형을 일반화하는 과정에 따라 포아송 클러스터 강우생성모형은 Bartlett-Lewis Rectangular Pulse (BLRP) 모형과 Neyman-Scott Rectangular Pulse (NSRP) 모형으로 구분된다.

3.2 BLRP 모형과 NSRP 모형

BLRP 모형과 NSRP 모형 모두 포아송 클러스터 모형으로, 두 모형의 차이점은 매개변수 추정을 위한 통계치에 3차 모멘트와 무강우 비율을 포함한 여부이며, 사실상 강우 생성 원리가 비슷하므로 교차 사용 역시 가능하다. 다만, NSRP 모형의 매개변수가 5개, BLRP 모형의 매개변수가 6개로, NSRP 모형의 매개변수가 1개 적어 매개변수 추정에 용이하며, 고차모멘트를 고려할 수 있다는 측면에서 극치강수량 추정에 상대적으로 장점을 가지고 있다(Cowpertwait et al., 1996). 이러한 점을 고려하여 본 연구에서는 NSRP 모형을 채택하여 연구를 진행하였다.

NSRP 모형은 점과정(point process)을 따르는 강우 생성 모형으로, 강우의 발생, 강우 셀(rain cell)의 강우강도 및 지속시간의 분포로 표현된다. Table 1에 제시한 NSRP 모형의 5개 매개변수는 강우의 물리적 특성을 고려하여 적용된 확률분포형 매개변수를 나타낸다. 최적화를 위해 설정한 매개변수의 범위 역시 Table 1에 제시하였다. NSRP 모형의 매개변수 최적화를 위한 통계적 모멘트는 Eqs. (1)~(4c)와 같이 나타낼 수 있다(Rodriguez-Iturbe et al., 1987). 여기서 지속기간 h시간 동안의 강우량 평균은 $E [R_{i}^{(h)}]$ , 강우량의 분산은 $V a r [R_{i}^{(h)}]$ , 강우량의 지체시간(lag time) $l = 1$ 에 따른 공분산은 $C o v [R_{i + 1}^{(h)}, R_{i}^{(h)}]$ 이다. $S k e w [R_{i}^{(h)}]$ 는 h시간 동안의 강우량의 왜곡도를 의미한 다. 본 연구에서는 통계치로 활용할 1시간 평균, 1시간 분산, 24시간 분산, 24시간 자기상관계수, 1시간 왜도 및 24시간 왜도를 산정하기 위하여 지속기간 h를 1 또는 24로 설정하였다. 매개변수의 범위를 정확하게 설정하는 것은 현실적으로 어려울 뿐만 아니라, 최적화 과정에서 제시된 매개변수 범위에서 최적의 조합을 찾는 방식이라 매개변수의 범위를 수정하게 되면 추정되는 매개변수 집합이 달라질 수 있다. 이러한 특징은 통계적 모형의 매개변수 추정 시 필요한 우도함수(likelihood)를 정의하는 것이 어렵기 때문이며, 최적화를 통한 매개변수 추정에서 적은 관측치(통계치) 정보로 인해 나타나는 문제라고 할 수 있다. 따라서, 매개변수 추정에 대한 어려움과 함께 매개변수의 변동성도 클 수 밖에 없다. NSRP 모형은 5개의 확률분포형으로 이루어져 다음 과정을 순차적으로 진행함으로써 구축할 수 있다.

Table 1.

Parameters of NSRP model and their ranges for optimization

Parameters	Variables	Minimum	Maximum
$λ$	Mean waiting time between storm origins	0.001	0.02
$β$	Mean waiting time for raincell followed by the storm origins	0.02	0.5
$ν$	Mean number of raincells for the storm	0.1	100
$η$	Mean duration of raincells	0.01	60
$ξ$	Mean rate of raincells	0.01	4

1) 강우사상의 시작점(storm origin)을 선정하기 위해 매개변수 $λ$ 를 가지는 지수분포를 구한다.

2) 선정된 강우 시작점에 대하여 매개변수 $ν$ 를 사용한 기하함수로 각 강우 군집의 강우세포(raincell) 수를 정한다.

3) 강우세포 수가 정해지면 매개변수 $β$ 를 사용한 지수분포로 각 강우세포의 위치를 결정한다.

4) 강우세포의 위치가 정해지면 매개변수 $η$ 를 사용한 지수분포로 강우세포의 지속기간을 정한다.

5) 강우세포의 지속기간이 정해지면 매개변수 $ξ$ 를 사용한 지수분포로 강우세포의 강우강도를 정한다.

6) 정해진 강우세포의 지속기간에 대한 강우강도를 중첩한다.

(1)

E [R_{i}^{(h)}] = λ ν h / (η ξ)

(2)

V a r [R_{i}^{(h)}] = λ / η^{3} (η h - 1 + e^{- η h}) (4 ν / η^{2} + (ν^{2} β^{2} / (ξ^{2} β (β^{2} - η^{2})))) - λ (β h - 1 + e^{- β h}) (ν^{2} / (ξ^{2} β (β^{2} - η^{2})))

(3)

C o v [R_{i + 1}^{(h)}, R_{i}^{(h)}] = λ / η^{3} {(1 - e^{- η h})}^{2} (e^{- η (l - 1) h}) (2 ν / ξ^{2} + 0.5 (ν^{2} β^{2})) / (ξ^{2} (β^{2} - η^{2})) - λ {(1 - e^{- β h})}^{2} (e^{- β (l - 1) h}) ν^{2} / (2 ξ^{2} β (β^{2} - η^{2}))

(4a)

S k e w [R_{i}^{(h)}] = 36 λ ν ξ^{- 3} (η h - 2 + η h e^{- η h} + 2 e^{- η h}) / η^{4} + 6 λ ξ^{- 3} ν^{2} F / (2 η^{4} β {(β^{2} - η^{2})}^{2}) + λ ξ^{- 3} ν^{3} G / (2 η^{4} β (η^{2} - β^{2}) (η - β) (2 β + η) (β + 2 η))

(4b)

F = - 2 η^{3} β^{2} e^{- η h} - 2 η^{3} β^{2} e^{- β h} + η^{2} β^{3} e^{- 2 η h} + 2 η^{4} β e^{- η h} + 2 η^{4} β e^{- β h} + 2 η^{3} β^{2} e^{- (η + β) h} - 2 η^{4} β e^{- (η + β) h} - 8 η^{3} β^{3 h} + 11 η^{2} β^{3} - 2 η^{4} β + 2 η^{3} β^{2} + 4 η β^{5 h} + 4 η^{5} β h - 7 β^{5} - 4 η^{5} + 8 β^{5} e^{- η h} - β^{5} e^{- 2 η h} - 2 h η^{3} β^{3} e^{- η h} - 12 η^{2} β^{3} e^{- η h} + 2 h η β^{5} e^{- η h} + 4 η^{5} e^{- β h}

(4c)

G = 12 η^{5} β e^{- β h} + 9 η^{4} β^{2} + 12 η β^{5} e^{- η h} + 9 η^{2} β^{4} + 12 η^{3} β^{3} e^{- (η + β) h} - η^{2} β^{4} e^{- 2 η h} - 12 η^{3} β^{3} e^{- β h} - 9 η^{5} β - 9 η β^{5} - 3 η β^{5} e^{- 2 η h} - η^{4} β^{2} e^{- 2 β h} - 12 η^{3} β^{3} e^{- η h} + 6 η^{5} β^{2} h - 10 β^{4} η^{3} h + 6 β^{5} η^{2} h - 10 β^{3} η^{4} h + 4 β^{6} η h - 8 β^{2} η^{4} e^{- β h} + 4 β η^{6} h + 12 β^{3} η^{3} - 8 β^{4} η^{2} e^{- η h} - 6 η^{6} - 6 β^{6} - 2 η^{6} e^{- 2 β h} - 2 β^{6} e^{- 2 η h} + 8 η^{6} e^{- β h} + 8 β^{6} e^{- η h} - 3 β η^{5} e^{- 2 β}

지점별 매개변수 추정이 모형 적용보다 선행되어야 하며, 본 연구는 강수 모의 자료의 계절적 특성을 고려하기 위하여 월별로 매개변수를 추정하였다. 모의 강우시계열과 관측시계열의 통계적 유사성을 통해 매개변수를 결정하였으며, Eq. (5)의 목적함수(OF)를 최소로 하는 매개변수의 집합을 도출하였다. 즉, 관측 강우시계열과 모의 강우시계열의 통계치의 오차 합이 최소가 되는 조합을 찾는 과정이다. 목적함수 최소화를 위하여 MATLAB의 최적화 툴박스인 fmincon을 사용하였다. 많은 양의 자료를 최적화하는 문제에 사용되는 fmincon은 비선형 다변수 함수에서 제약조건을 고려하여 최솟값을 계산하는 함수로, 계산방법은 Active-set을 이용하였다(Yu et al., 2021).

(5)

O F = \sum_{k = 1}^{n} w_{k} {(1 - \frac{M_{k} (\vec{θ})}{m_{k}})}^{2}

여기서, M_k는 매개변수의 집합 $\vec{θ} (λ, β, ν, η, ξ)$ 로부터 생성된 가상의 모의 강우시계열에서 추정된 통계값(평균, 분산, 자기상관계수 등)을 의미한다. m_k는 관측 통계값(평균, 분산, 자기상관계수 등)을 나타내는 상수항이고 w_k는 통계값에 적용하는 가중치를 나타낸다. 첨자 k는 강수의 통계값 종류이며, n은 매개변수 추정을 위해 사용한 통계값의 전체 수를 의미한다. 가중치 w_k는 기존 논문들에서 제시한 값을 기준으로 최적의 결과를 도출하기 위해 매뉴얼하게 수정하여 적용하였다.

4. 연구결과

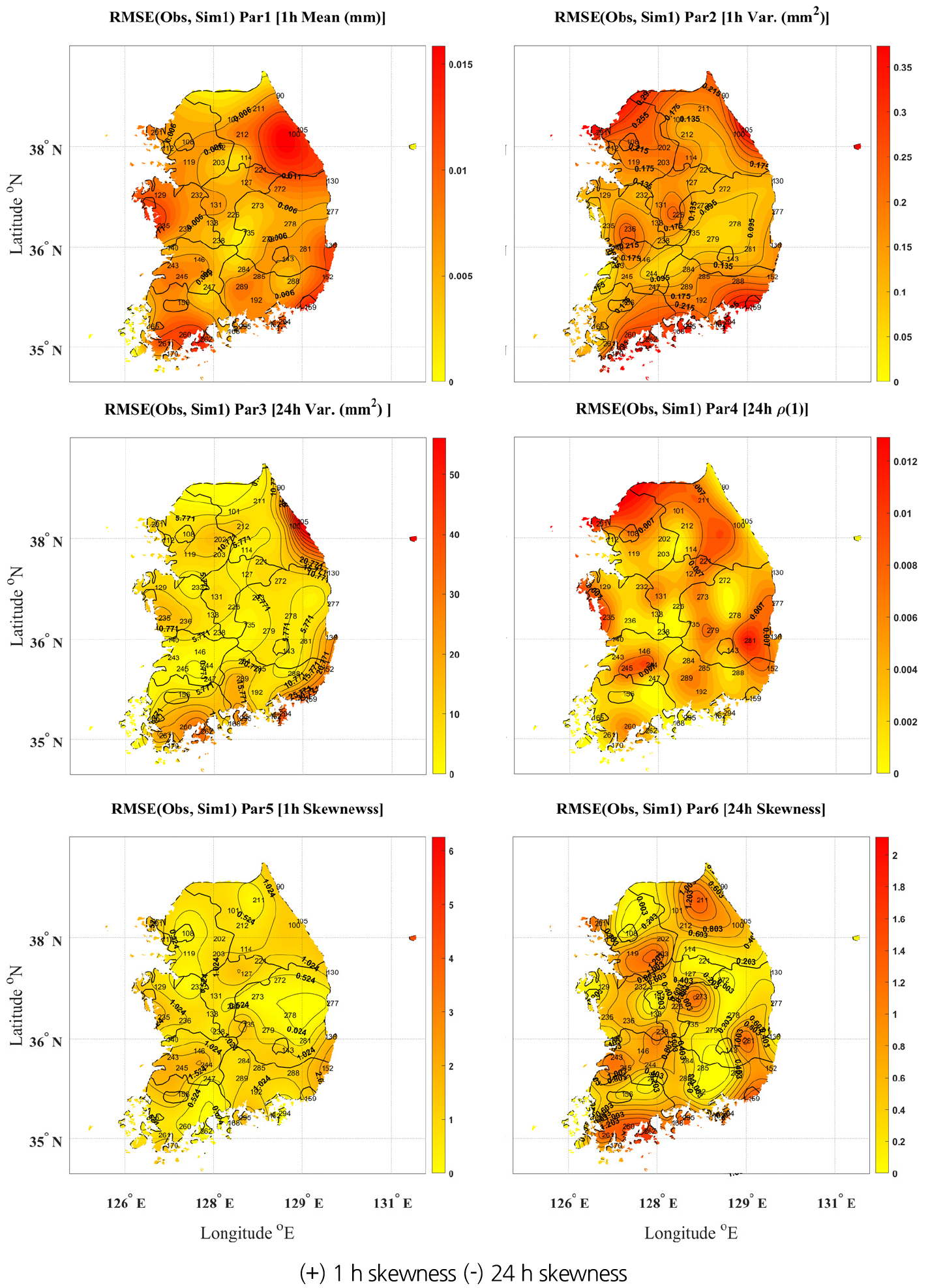
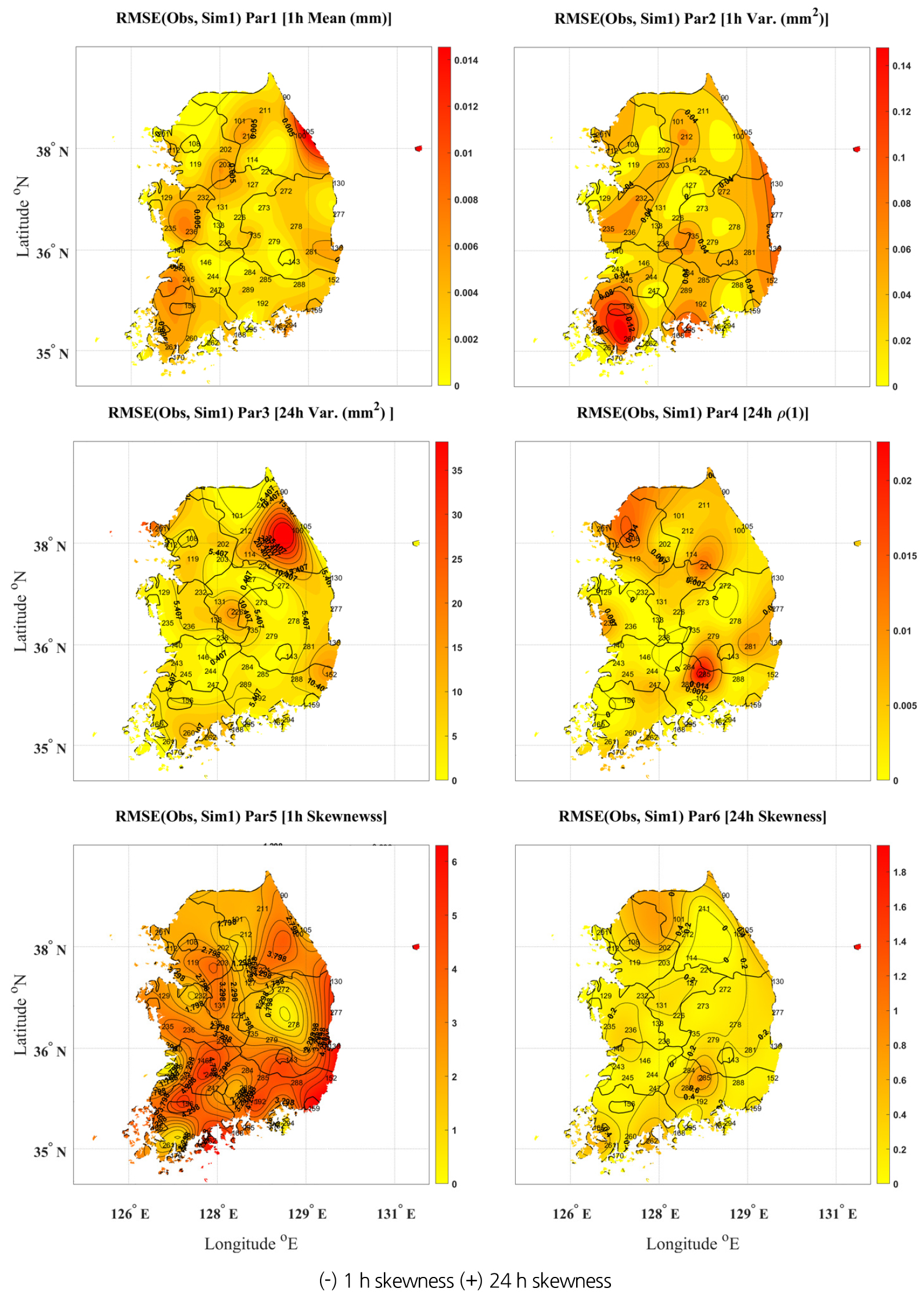
Figs. 2~4는 매개변수 추정에 활용하는 목적함수 종류에 따라 다른 모의 결과를 공간적으로 비교한 것으로, 모의값과 관측값의 오차인 RMSE 값을 도식화하여 황색에서 적색의 범위 중 황색에 가까울수록 오차가 적고 적색에 가까울수록 오차가 커짐을 의미한다. 1차, 2차 모멘트는 공통적으로 목적함수에 포함하였고, 3차 모멘트 포함에만 차이를 주어 Fig. 2는 1시간 왜곡도만 목적함수에 포함한 경우, Fig. 3은 24시간 왜곡도만 포함한 경우이고 Fig. 4는 1시간, 24시간 왜곡도를 모두 목적함수에 포함한 경우를 나타내었다. Figs. 2~4에서 (+), (-)는 특정 목적함수의 포함 여부를 나타내며, Par1~Par6은 차례대로 1시간 평균, 1시간 분산, 24시간 분산, 24시간 자기상관계수, 1시간 왜곡도 및 24시간 왜곡도를 의미한다. 1시간 또는 1시간과 24시간을 동시에 포함하는 경우, 24시간 왜곡도만을 고려한 경우에 비해 1시간 평균값 추정에 불리하였다. 반면 24시간 왜곡도만을 포함하는 경우, 1시간 왜곡도 추정 시 오차가 다소 커지는 것을 확인할 수 있다. 전반적으로 1시간과 24시간 왜곡도를 모두 포함하는 경우가 통계치를 복원하는데 유리한 것으로 분석되었다. 왜곡도를 포함하는 경우 왜곡도를 복원하는데 매우 효과적이었지만, 평균과 분산 등 다른 통계치 추정에 있어서 일부 오차가 커지는 경향을 확인할 수 있었다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F2.jpg

Fig. 2.

Spatial distribution of six different rainfall statistics obtained from an objective function with the inclusion of the 1-hour skewness

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F3.jpg

Fig. 3.

As in Fig. 2, but for the inclusion of 24-hour skewness

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F4.jpg

Fig. 4.

As in Fig. 2, but for the inclusion of both 1-hour skewness and 24-hour skewness

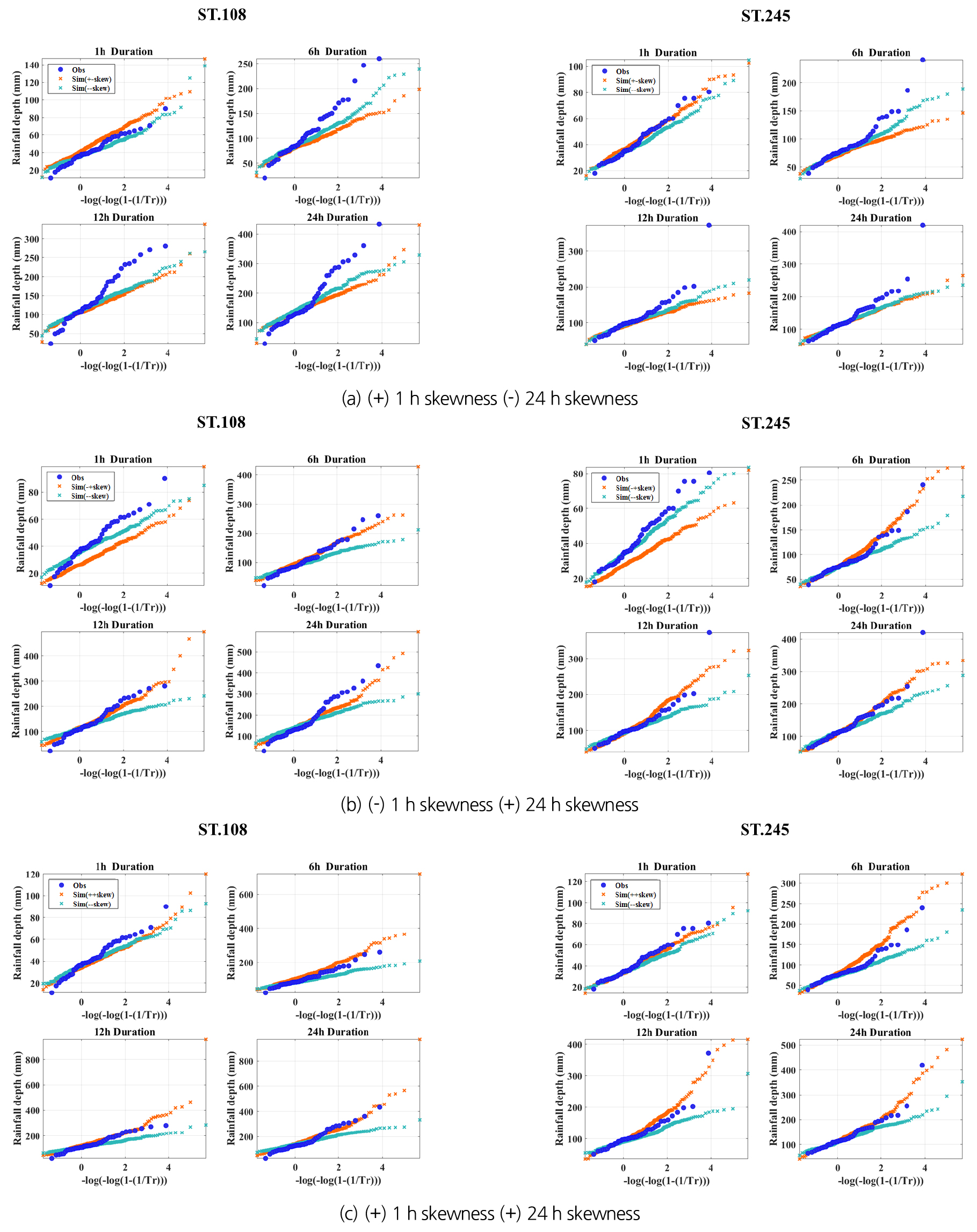
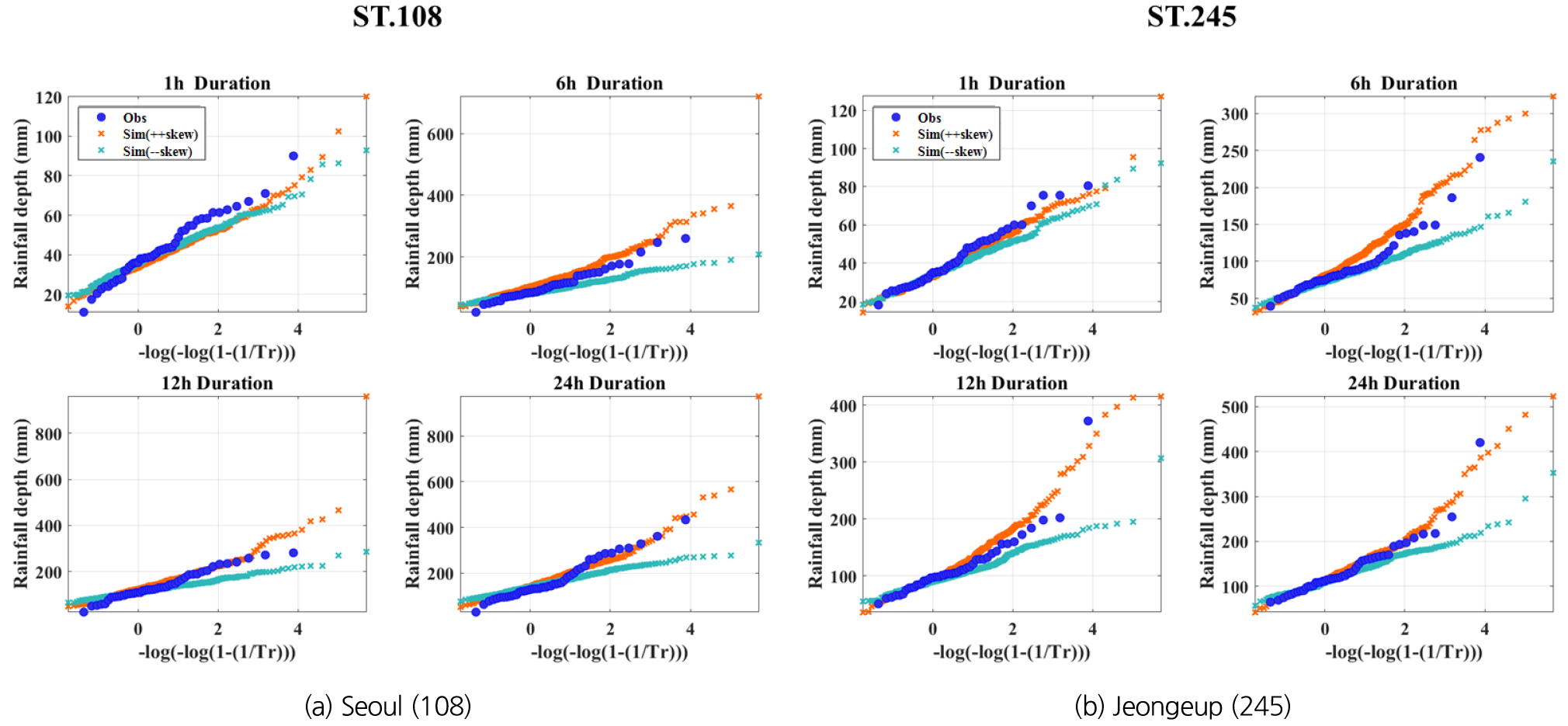
Fig. 5는 왜곡도 고려에 따른 극치값 재현 특성을 검토하기 위하여, 서울(108)과 정읍(245) 관측지점을 대상으로 Gumbel 확률지(probability plot)를 통해 비교한 그림이다. “Obs”는 관측값을 의미하며 Fig. 5(a)의 “Sim(+-skew)”은 1시간 왜곡도를 목적함수에 포함한 경우이고 Fig. 5(b)의 “Sim(-+skew)”은 24시간 왜곡도만을 목적함수에 포함한 경우, Fig. 5(c)의 “Sim(++skew)”은 1시간, 24시간 왜곡도를 모두 목적함수에 포함한 경우, “Sim(--skew)” 모의값은 왜곡도를 목적함수에서 제외한 경우이다. 모의 결과를 보면, (a)는 지속시간 1시간에 대한 극치값을 잘 추정하지만, 지속시간이 길어질수록 현저히 관측값과 차이가 나는 것을 확인할 수 있다. (b)는 지속시간 1시간에 대한 극치값을 다소 과소 추정하지만, 지속시간이 길어질수록 관측값과 유사한 분포 특성을 보여주고 있다. 앞서 언급된 통계치 및 극치 강수량의 분포 특성에 대한 재현 결과에서 오차가 일부 증가하더라도, 극치값 추정 목적에 부합하는 조건으로는 (c)와 같이 1시간 왜곡도와 24시간 왜곡도를 모두 목적함수에 포함하는 방법이 적합하다고 판단하였다.

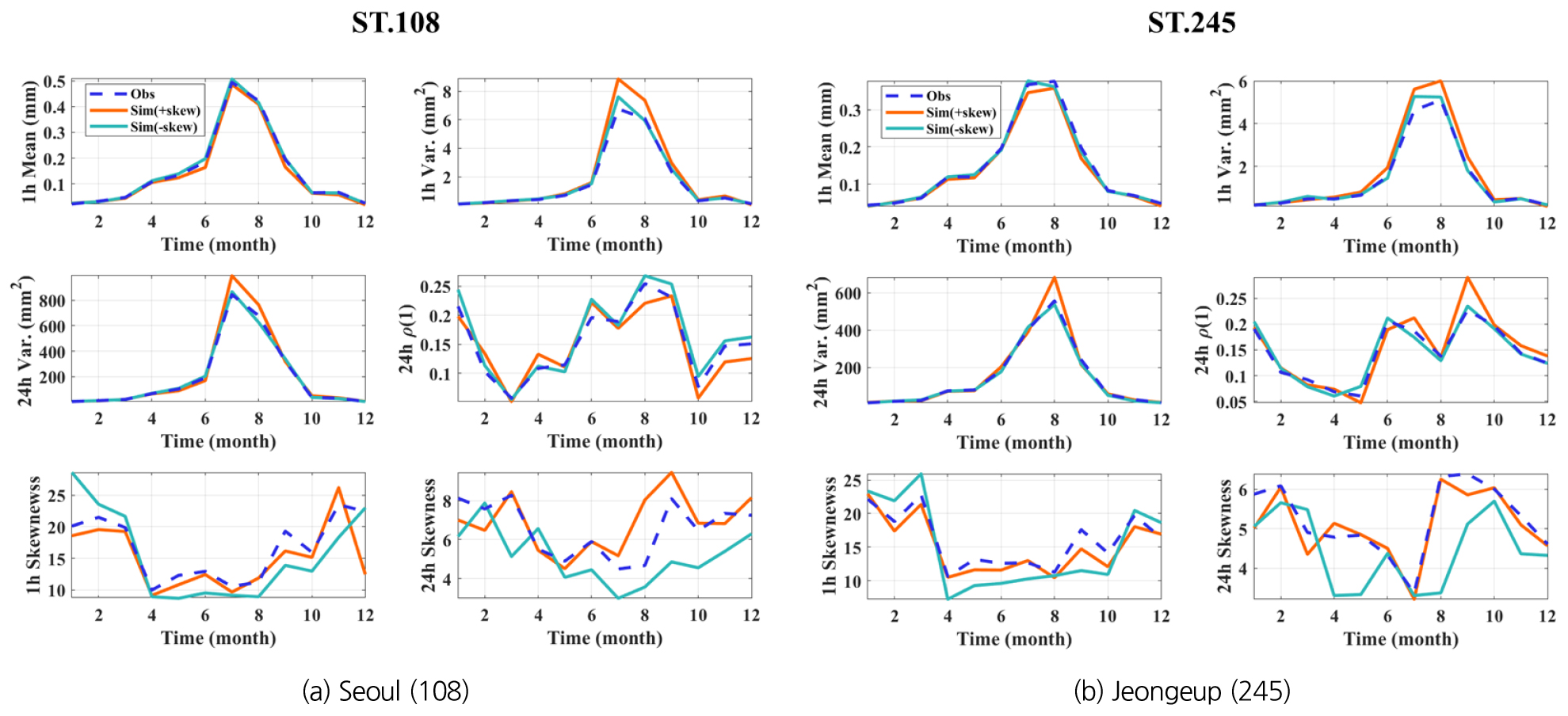
본 연구에서 제시한 방법론을 토대로 300년의 강수량을 모의하여 관측값과 비교한 결과를 대표 지점(서울과 정읍)에 대하여 Fig. 6에 나타내었다. Obs 및 Sim(+skew), Sim(-skew)은 관측시계열 및 모의시계열로부터 추출한 통계량의 평균을 의미한다. 각 지점이 독립적이라는 가정 아래에 모의한 1차 모의 시계열을 대상으로 추정한 통계치다. “Obs”는 관측값, “Sim(+skew)” 모의값은 1시간 왜곡도와 24시간 왜곡도를 모두 목적함수에 포함한 경우이고, “Sim(-skew)” 모의값은 두 왜곡도 값을 모두 목적함수에서 제외한 경우이다. 제시한 결과에서 볼 수 있듯이, Sim(+skew)와 Sim(-skew)를 비교하면 상대적으로 Sim(+skew)가 관측값 복원에 유리한 것을 확인할 수 있다.

매개변수 추정에 대한 오차는 Table 2에 나타내었다. 관측값과 두 모의값의 오차값과 오차율로, 앞서 언급하였듯이 1차, 2차 모멘트는 Sim1이 Sim2에 비해 다소 오차가 큰 편이지만, 극치값 재현 측면에서 3차 모멘트의 오차가 작아 유리함을 알 수 있다. Fig. 7은 모의 자료에서 추출한 연최대강수량을 관측값과 확률지를 통해 비교한 결과다. 확률지는 Gumbel 확률지를 활용하였으며, 1시간 지속시간에 대한 모의 결과는 극치값이 과소 추정되지만, 24시간으로 지속시간이 커질수록 추정 결과가 개선되는 양상을 보여주고 있다. Fig. 5와 비교하면, 여러 지속시간에 대한 극치강우 재현능력이 두 왜곡도값을 모두 목적함수에 포함했을 때 더 뛰어남을 확인할 수 있다.

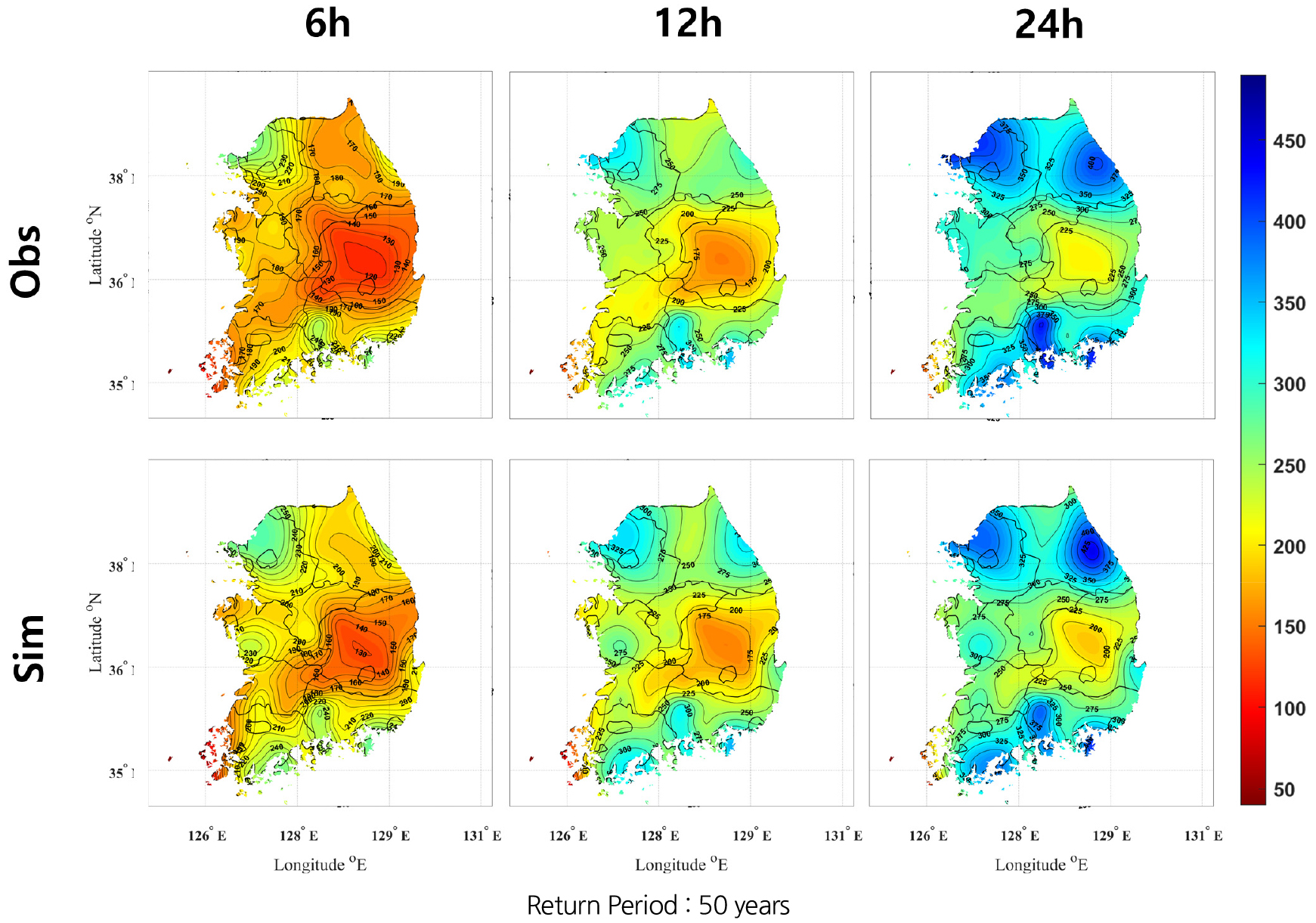
두 왜곡도값을 모두 목적함수에 포함한 NSRP 모형을 통해 생성한 모의강우자료에 대하여 빈도 분석한 결과 역시 관측값을 잘 재현하는 것을 확인할 수 있었다. Fig. 8은 관측값과 모의값에 대하여 50년 빈도의 강우를 지속시간별로 도시한 것으로, 우리나라의 자료연한을 고려할 때 모형의 검증 목적에서는 50년 빈도의 확률강우량 비교가 합리적이라고 판단하여 제시하였다. 확률강수량의 공간적인 변동성을 효과적으로 재현하고 있는 것을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F5.jpg

Fig. 5.

Comparison of Gumbel probability plots with the inclusion of skewness in the objective function - Seoul (108) and Jeongeup (245)

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F6.jpg

Fig. 6.

Comparison of rainfall statistics obtained from NSRP model - Seoul (108) and Jeongeup (245)

Table 2.

Comparison of rainfall statistics over different object functions

Station No.		First Moment (Mean)				Second Moment (Variance)				Third Moment (Skewness)
		1 hr Mean (mm)		1 hr Var. (mm²)		24 hr Var. (mm²)		24 hr Autocorr.		1 hr Skew.		24 hr Skew.
108	Sim1	0.1410	5.66%	1.9630	22.8%	210.87	9.19%	0.1486	3.33%	15.112	9.18%	6.8609	4.67%
	Obs	0.1495		1.5984		193.11		0.1537		16.640		6.5549
			1.76%		5.58%		0.37%		6.94%		6.21%		21.31%
	Sim2	0.1521		1.6876		193.83		0.1644		15.606		5.1581
245	Sim1	0.1365	5.28%	1.6153	18.8%	148.74	6.04%	0.1527	5.27%	15.053	5.83%	5.0776	3.04%
	Obs	0.1441		1.3596		140.27		0.1450		15.986		5.2366
			0.72%		4.68%		2.76%		0.16%		6.25%		15.0%
	Sim2	0.1431		1.4232		136.40		0.1453		14.986		4.4507

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F7.jpg

Fig. 7.

Comparison of Gumbel probability plots for Seoul (108) and Jeongeup (245) stations

https://static.apub.kr/journalsite/sites/kwra/2022-055-07/N0200550706/images/kwra_55_07_06_F8.jpg

Fig. 8.

Comparison of design rainfalls between simulated and observed annual maximum series for a 1 in 50-year events with different durations

5. 결 론

수자원 설계, 계획 및 수문 현상 모의 연구에 필요한 강우 자료의 관측 연한 문제를 해결하기 위해 확률론적 강우생성모형에 대한 연구가 활발하며, 시간강우량 모의에는 일반적으로 포아송 클러스터 강우생성모형을 활용한다. 비교적 적은 수의 매개변수로 강수시계열을 모의 생성할 수 있는 장점이 있다.

본 연구에서 적용한 포아송 클러스터 강우생성모형은 NSRP 모형으로, 일반적으로 목적함수로 활용하는 1, 2차 모멘트뿐만 아니라 3차 모멘트까지 사용하여 매개변수 추정과 극치강수량 추정에 정확도를 높여 모의강수시계열을 생성하였다. 본 연구를 통해 얻은 연구 결과를 요약하면 다음과 같다.

1) NSRP 모형의 목적함수의 평균, 분산, 자기상관계수 만을 포함하는 경우 강우의 통계적 특성을 전반적으로 재현하는 것으로 평가되었다. 왜곡도의 경우에도 전반적인 경향성은 복원 가능하였지만, 강수가 집중되는 여름의 왜곡도 추정에 한계가 있었으며, 이로 인해 설계강수량의 과소 추정 문제가 크게 나타났다.

2) NSRP 모형의 매개변수 추정 시 왜곡도를 목적함수에 추가하는 경우 일반적인 강우의 통계적 특성을 효과적으로 재현하면서 왜곡도 재현에도 유리한 것을 확인할 수 있었으며, 설계강수량 추정 시에도 기존 매개변수 추정 방법에 비해 과소 추정 문제를 개선할 수 있었다.

3) 매개변수 추정 시 왜곡도를 목적함수에 추가하게 되면 분산의 복원 측면에서 그렇지 않은 경우에 비해 강수가 집중되는 여름 동안에 다소 과대 추정되는 문제를 확인할 수 있었다. 이는 왜곡도를 복원하면서 발생하는 문제로 판단된다. 이러한 문제는 Eq. (5)에서 제시된 목적함수의 분산 및 왜곡도에 적용되는 가중치 w를 조정하면서 개선이 가능할 것으로 판단되며, 향후 가중치에 대한 추정도 최적화 관점에서 연구가 필요할 것으로 판단된다.

매개변수 최적화 특성상 매개변수의 범위에 따라 추정되는 매개변수 사이의 상호작용으로 매개변수가 변동하게 된다. 이러한 문제를 개선하기 위하여 고려되는 통계치에 대한 가중치에 변화를 주거나 범위 조정과 더불어, 유역 내 여러 지점 간의 상관성을 고려한 다지점 NSRP 모형 개발 연구를 추가 진행할 예정이다. 또한, 추계학적 강우모의 모형은 기후변화로 인한 자료의 비정상성을 고려하지 못한다는 단점이 있으므로, 은닉 마코프 모형(hidden Markov model, HMM)을 이용하여 기후변동성을 고려한 비정상성 강우모의를 통해 연구를 확장할 수 있을 것으로 보인다.

Acknowledgements

본 결과물은 환경부의 재원으로 한국환경산업기술원의 수생태계 건강성 확보 기술개발사업의 지원을 받아 연구되었습니다(과제번호:2021003030004).

Conflicts of Interest

The authors declare no conflict of interest.

References

Boughton, W., and Droop, O. (2003). "Continuous simulation for design flood estimation - a review." Environmental Modelling & Software, Vol. 18, No. 4, pp. 309-318. 10.1016/S1364-8152(03)00004-5

Cowpertwait, P.S.P., O'Connell, P.E., Metcalfe, A.V., and Mawdsley, J.A. (1996). "Stochastic point process modelling of rainfall. I. Single-site fitting and validation." Journal of Hydrology, Vol. 175, No. 1, pp. 17-46. 10.1016/S0022-1694(96)80004-7

Kim, D., Kwon, H.H., Lee, S.O., and Kim, S. (2016). "Regionalization of the Modified Bartlett-Lewis rectangular pulse stochastic rainfall model across the Korean Peninsula." Journal of Hydro-Environment Research, Vol. 11, pp. 123-137. 10.1016/j.jher.2014.10.004

Kim, D., Shin, J.Y., Lee, S.O., and Kim, T.W. (2013). "The application of the poisson cluster rainfall generation model to the flood analysis." Journal of Korea Water Resources Association, Vol. 46, No. 5, pp. 439-447. 10.3741/JKWRA.2013.46.5.439

Kim, J. (2018). A development of multisite hourly rainfall simulation model using bayesian poisson cluster rainfall generators. Ph. D. Dissertation, Jeonbuk National University. pp. 7-20.

Kim, S.D., Yoo, C.S., Kim, J.H., and Yoon, Y.N. (2000). "A study of temporal characteristics from multi-dimensional precipitation model." Journal of Korea Water Resources Association, Vol. 33, No. 6, pp. 783-791.

Lee, J., and Kim, Y. (2016). "A spatial analysis of Neyman-Scott rectangular pulses model using an approximate likelihood function." Journal of the Korean Data and Information Science Society, Vol. 27, No. 5, pp. 1119-1131. 10.7465/jkdi.2016.27.5.1119

Rodriguez-Iturbe, I., Cox, D.R., and Isham, V. (1987). "Some models for rainfall based on stochastic point processes." Proceedings of the Royal Society of London. A. Mathematical, Physical and Engineering Sciences, Vol. 410, No. 1839, pp. 269-288. 10.1098/rspa.1987.0039

So, B.J., Kwon, H.H., Kim, D., and Lee, S.O. (2015). "Modeling of daily rainfall sequence and extremes based on a semiparametric Pareto tail approach at multiple locations." Journal of Hydrology, Vol. 529, pp. 1442-1450. 10.1016/j.jhydrol.2015.08.037

Verhoest, N., Troch, P.A., and De Troch, F.P. (1997). "On the applicability of Bartlett-Lewis rectangular pulses models in the modeling of design storms at a point." Journal of Hydrology, Vol. 202, No. 1-4. pp. 108-120. 10.1016/S0022-1694(97)00060-7

Yu, J.U., Park, M.H., Kim, J.G., and Kwon, H.H. (2021). "Evaluation of conceptual rainfall-runoff models for different flow regimes and development of ensemble model." Journal of Korea Water Resources Association, Vol. 54, No. 2, pp. 105-119. 10.3741/JKWRA.2021.54.2.105

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Evaluation of extreme rainfall estimation obtained from NSRP model based on the objective function with statistical third moment

ABSTRACT

MAIN

Fig. 1.

ASOS Weather stations over South Korea

Table 1.

Parameters of NSRP model and their ranges for optimization

(1)

(2)

(3)

(4a)

(4b)

(4c)

(5)

Fig. 2.

Spatial distribution of six different rainfall statistics obtained from an objective function with the inclusion of the 1-hour skewness

Fig. 3.

As in Fig. 2, but for the inclusion of 24-hour skewness

Fig. 4.

As in Fig. 2, but for the inclusion of both 1-hour skewness and 24-hour skewness

Fig. 5.

Comparison of Gumbel probability plots with the inclusion of skewness in the objective function - Seoul (108) and Jeongeup (245)

Fig. 6.

Comparison of rainfall statistics obtained from NSRP model - Seoul (108) and Jeongeup (245)

Table 2.

Comparison of rainfall statistics over different object functions

Fig. 7.

Comparison of Gumbel probability plots for Seoul (108) and Jeongeup (245) stations

Fig. 8.

Comparison of design rainfalls between simulated and observed annual maximum series for a 1 in 50-year events with different durations

Acknowledgements

Conflicts of Interest

References