1. 서 론
2. 연구 방법
2.1 연구 대상
2.2 구조방정식모형
2.3 PLS-SEM
2.4 연구 가설 및 연구 모형
3. 연구 결과
3.1 반영적 측정모형 평가 결과
3.2 구조모형 평가 결과
4. 결 론
1. 서 론
최근 세계 곳곳에서는 대형 규모의 산불이 빈번히 발생하고 있으며 이로 인한 피해가 막대하다. 2019년 호주에서는 9월 이후 약 3만 건 이상의 산불이 발생하여 약 1,900만 ha에 달하는 산림이 소실되었고, 33명의 인명피해와 만여 채의 시설물 피해가 발생했으며, 산불 발생으로 인한 연기는 주변 국가인 뉴질랜드 뿐 아니라 남아메리카 대륙의 대기질에도 영향을 미쳤다(NIFoS, 2020). 2020년 미국 서부에서는 9월부터 극심한 폭염과 강풍의 영향으로 100건 이상의 대형 산불이 발생하여 약 331만 ha가 소실되었고 피해액은 3조원 이상으로 추정된다(GACC, 2020).
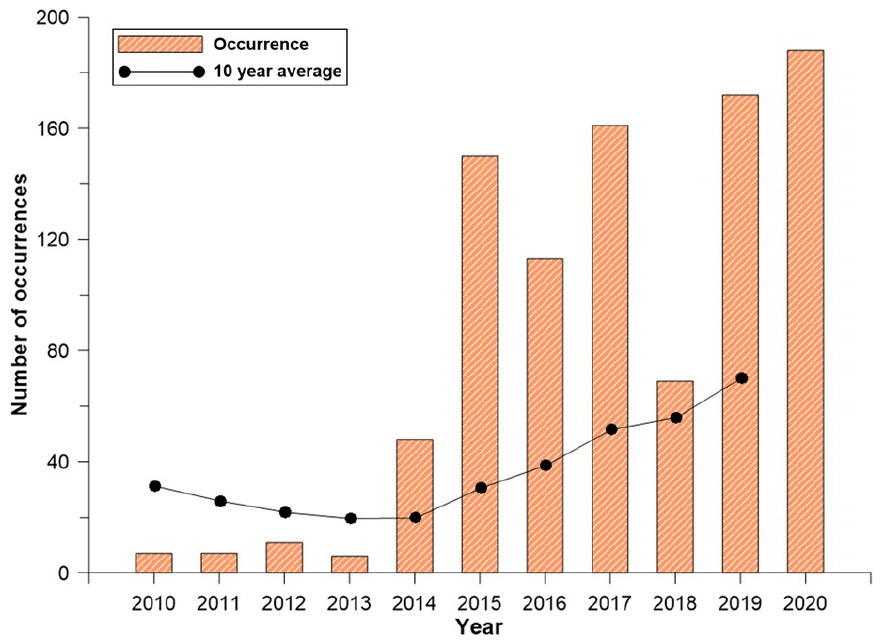
우리나라 또한 산불이 빈번하게 발생하고 있으며, 지난 10년 간(2010-2019) 평균적으로 매해 440건의 산불이 발생하였고 이로 인한 피해면적은 약 857 ha이다(KFS, 2020). 2019년에는 총 653건의 산불이 발생하여 최근 10년 평균 대비 약 47% 증가하였으며, 산불 피해면적은 전년 대비 약 73%가 증가하였다. 2020년의 경우, 12월 2일을 기준으로 총 579건의 산불이 발생하여 10년 평균을 상회하는 수치를 보였다(Kim, 2020).
2010년부터 2019년까지의 10년간 원인별 산불 발생 현황을 살펴보면, 우리나라의 산불은 주로 등산객들의 실수로 인한 입산자 실화와 소각 과정에서 발생한 소각 산불이 각각 34%와 30%를 차지하며, 나머지 또한 대부분 인위적인 요인으로 인해 발생한다(KFS, 2020). 하지만, 산불의 발화, 연소 그리고 확산은 기온, 습도, 풍속 등 산불의 연소 환경을 구성하는 기상인자들과 높은 상관관계를 보인다(Cunningham and Martell, 1973). 또한 기후변화로 인해 건조일수가 증가하고 강수량이 감소하면서 가뭄 발생이 증가하는 것은 산불의 범위와 강도 및 빈도에 영향을 미치는 것으로 나타났다(Littell et al., 2016; KFS, 2020). 뿐만 아니라, 산불로 인해 대기 중으로 이산화탄소와 에어로졸이 다량 배출되는데, 이산화탄소와 에어로졸은 기후변화를 초래하는 주요인으로 다시 산불 위험을 증가시키므로 기후변화-가뭄-산불의 악순환으로 이어지게 된다(Clark et al., 1996).
산불 위험이 증가함에 따라 국내·외에서는 산불과 기상인자, 그리고 기후변화의 연관성을 분석하는 연구들이 다수 진행되었다. Lee (2009)는 1996년부터 2006년까지의 산불 피해면적과 기상요인의 연관성을 분석하였는데 강수, 습도, 풍속 등의 기상인자는 산불과 관련이 있지만 평균기온은 크게 연관이 없는 것을 확인하였다. Sung et al. (2010)은 습도 및 강수일수 등의 인자가 산불의 증감추세에 영향을 미칠 수 있다는 것을 보였다. Kim et al. (2015)은 1990년대 이후 강원도 지역의 산불 피해면적을 종속변수로, 기상인자들을 독립변수로 하는 회귀분석을 수행하여 산불 피해면적에 평균풍속이 가장 큰 영향력을 가진다는 것을 확인하였다. Yoon and Won (2016)은 우리나라에서 표준강수지수(Standardized Precipitation Index, SPI)와 산불 발생빈도가 높은 상관관계를 가진다는 것을 입증하였다. 또한 Flannigan et al. (2000)이 대기대순환모델(General Circulation Models, GCMs)을 활용한 분석 결과 기후변화가 산불 피해와 강도를 증가시킨다는 것을 입증하였다. Marin et al. (2018)은 멕시코 산불자료의 분석을 통해 표준강수증발산지수(Standardized Precipitation Evapotranspiration Index, SPEI)와 화재 빈도 간의 연관성을 제시하였다.
변수들 간의 영향을 파악하기 위해 일반적으로 상관관계분석, 요인분석, 주성분분석, 회귀분석 등의 통계분석 기법들이 활용되었다. 그러나 이 방법들은 독립변수와 종속변수 간의 1차원 관계밖에 분석할 수 없으며, 각각의 기법들을 개별적으로 수행해야 하기 때문에 여러 인자들 간의 인과관계를 동시에 정량적으로 분석하기는 어렵다(Shin, 2018).
따라서 본 연구에서는 경기도를 대상으로 최근 5년 동안 발생한 산불과 기상 및 수문학적 요인들 간의 영향 관계를 정량적으로 파악하기 위하여 부분최소제곱 구조방정식모형(Partial Least Squares-Structural Equation Model, PLS-SEM)을 활용하였다. PLS-SEM은 경로분석, 회귀분석, 요인분석 등의 통계분석 기법들이 통합된 것으로, 여러 요인들 간의 복잡한 인과관계에 대한 해석이 유연하고 이에 대한 직·간접적인 인과의 정도를 정량적으로 파악할 수 있다.
2. 연구 방법
2.1 연구 대상
본 연구의 대상 지역인 경기도는 우리나라에서 산불이 가장 빈번히 발생하는 지역으로, Fig. 1에 나타난 것과 같이 지난 10년(2010-2019)간 평균 74.4회의 산불이 발생하였다(KFS, 2020). 특히 2020년 12월 3일을 기준으로 경기도는 2020년에만 204건의 산불이 발생하여 두 번째로 산불이 많이 발생한 경상북도에 비해 무려 106건이나 더 많다. 경기도에서는 2014년부터 산불 발생건수가 급격히 증가하는 양상을 보이는데 이는 기후변화로 인한 가뭄과 건조일수의 증가로 인한 것으로 분석된다(KFS, 2016; 2019; 2020). 경기도의 산불 피해면적은 광역시·도별 단위로 집계했을 때 네 번째로 크며, 강원도, 경상북도에 비해 피해가 적으나 매년 증가하는 추세이고, 발생 건수 또한 증가추세에 있어 대형 산불의 위험이 항상 존재하는 것으로 판단된다.
본 연구에서는 2015년부터 2020년 6월까지 시·군별로 집계된 총 840건의 산불을 대상으로 분석자료를 구축하였다. 산불 재난 위기관리 표준매뉴얼에 따르면 산불 발생의 감시 수단으로 산불 피해면적, 일 단위 산불 발생건수, 그리고 산불위험지수를 상시 모니터링하며, 이에 따라 산불 위기경보 등급을 구분하고 있다. 따라서 본 연구에서는 산불 발생 요인의 측정변수로 시·군별 단위의 산불 피해면적(AREA), 산불위험지수(INDEX), 산불 위기경보 등급(LEVEL)을 활용하였다(KFS, 2018). 분석 자료 중 기상학적 요인으로는 당일과 1-7일 이전, 8-14일 이전, 15-21일 이전의 평균기온(AT), 최고기온(HT), 일조시간(SSH), 평균 상대습도(ARH), 최소 상대습도(LRH), 실효습도(EH)와, 당일과 1주 전, 2주 전, 3주 전의 평균풍속(AW), 최고풍속(HW), 순간 최고풍속(IMW)을 측정변수로 활용하였으며, 수문학적 요인으로는 7일 누적, 14일 누적, 21일 누적, 28일 누적 선행 강수량(P)과 당월, 1개월 이전, 2개월 이전, 3개월 이전의 SPI와 SPEI, 그리고 연속건조일수(CDD)를 측정변수로 활용하였다. 기상학적 요인과 수문학적 요인의 측정변수들은 모두 기상관측소에서 기록된 지점 자료로, Thiessen 가중법을 활용해 시·군 단위로 변환한 후 분석에 활용하였다. 본 연구의 측정변수들을 Tables 1 and 2에, 측정변수들의 기초통계량을 Table 3에 나타냈다.
본 연구에서 활용한 측정변수 당 표본크기는 840개로 PLS-SEM을 활용하기에 충분한 크기를 가졌다고 판단하였다. Table 3에 나타난 바와 같이 왜도(Skew)와 초과첨도(Excess Kurtosis, E.K.)의 경우 총 17개의 변수들이 정규성 가정을 충족을 하기 위한 기준범위(-1, 1)를 벗어나지만 PLS-SEM은 분포에 대해 엄격한 적용이 요구되지 않으므로 문제가 없는 것으로 판단하였다.
Table 1.
Observed variables of hydrological factors and forest fire factor
Table 2.
Observed variables of meteorological factors
Table 3.
Basic statistics for observed variables
2.2 구조방정식모형
구조방정식모형(SEM)은 잠재변수들 간의 인과관계를 파악하기 위해 사용되는 통계분석 기법으로, 잠재변수 및 측정변수, 그리고 측정오차 등을 동시에 고려하여 인과관계를 분석하는 방법이다(Song and Lee, 2011). 구조방정식모형은 크게 최대우도를 이용해 측정변수 간의 공분산을 추정하는 공분산 기반 구조방정식모형(Covariance-Based Structural Equation Modeling, CB-SEM)과 최소 제곱을 이용해 설명되지 않은 예측오차를 최소화하는 부분최소제곱 구조방정식모형(PLS-SEM)으로 구분된다.
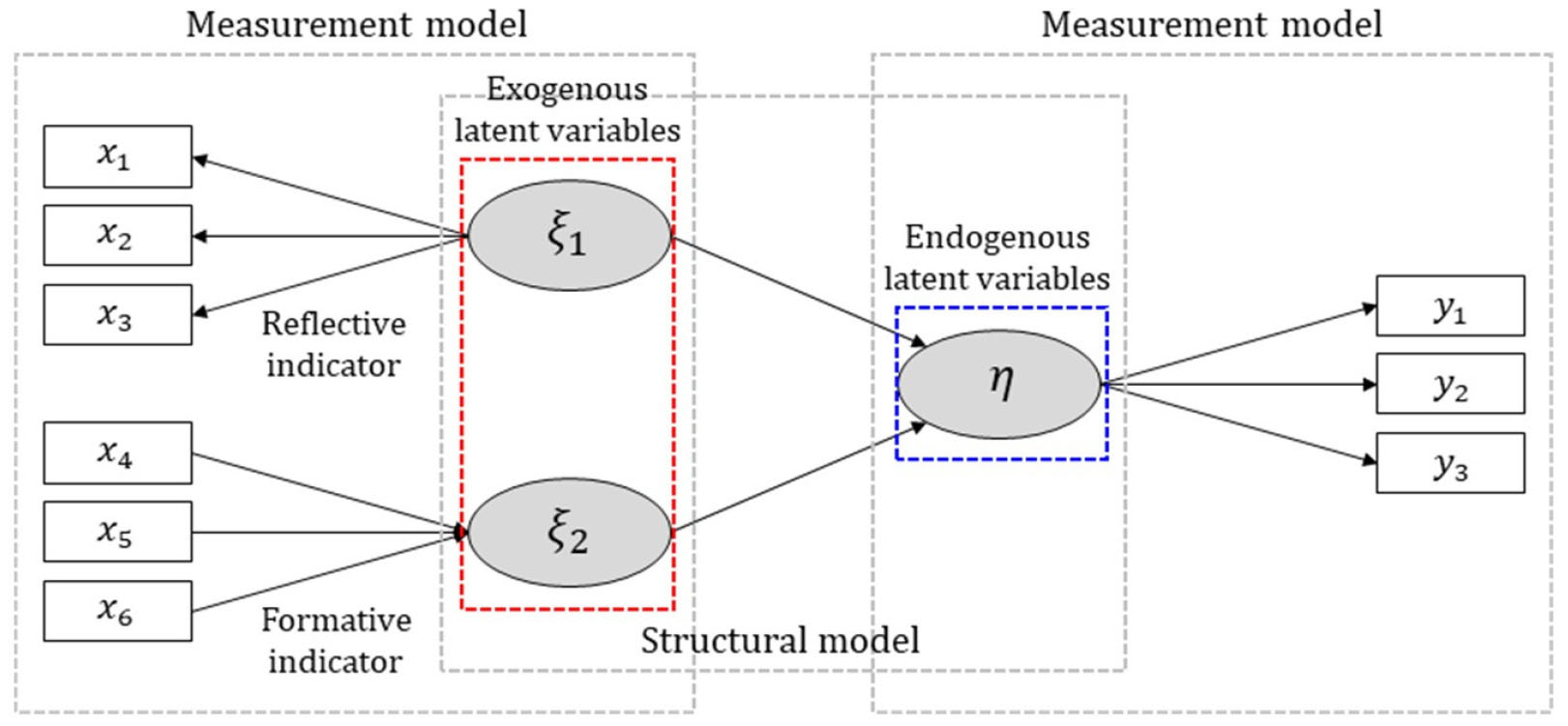
구조방정식모형에서 측정변수는 잠재변수(Latent variable)를 측정하기 위해 활용된 변수를 의미하며, 잠재변수는 측정변수를 통해 간접적으로 측정되는 변수를 의미한다. 잠재변수는 독립변수와 같이 다른 잠재변수에 영향을 미치는 외생잠재변수(Exogenous latent variable) 그리고 종속변수와 같이 영향을 받는 내생잠재변수(Endogenous latent variable)로 구분된다. 구조방정식모형은 Fig. 2와 같이 측정변수들()과 각 잠재변수들()의 인과관계를 나타내는 측정모형과 잠재변수들 간의 인과관계를 나타내는 구조모형의 결합으로 구성된다. 여기서 측정변수와 잠재변수의 인과 방향에 따라 반영적(Reflective) 측정모형과 형성적(Formative) 측정모형으로 구분되며, 구조방정식모형의 외생잠재변수 측정모형, 내생잠재변수 측정모형 그리고 구조모형은 Eqs. (1) ~ (3)과 같이 표현된다(Fornell and Larcker, 1981; Chin, 1998).
Eqs. (1) and (2)에서 와 는 , 의 측정변수 행렬을 의미하고, 와 는 와 에 대한 와 의 요인적재 행렬을, 그리고 와 는 와 에 대한 측정오차 벡터를 의미한다. Eq. (3)에서 와 는 내생잠재변수와 외생잠재변수의 벡터를 의미하며, 는 내생잠재변수의 오차 벡터, B와 는 각각 와 의 경로계수 행렬을 의미한다.
2.3 PLS-SEM
CB-SEM은 가장 일반적으로 활용되는 구조방정식모형으로 주로 이론의 검증을 위해 사용된다. 하지만 CB-SEM은 관측 자료의 정규성 가정을 엄격하게 준수해야하기 때문에 왜도와 초과첨도가 허용범위인 -1과 1사이의 값을 가져야만 한다. 또한, CB-SEM은 결과의 신뢰성 확보를 위해 최소 200개 이상의 표본을 필요로 한다(Shin, 2018). PLS-SEM은 CB-SEM의 여러 가지 한계를 극복할 수 있으며, 이론에 대한 연구가 부족한 경우 혹은 잠재변수의 예측이 목적일 경우 활용된다(Hair et al., 2012).
PLS-SEM은 모형의 유의성 검정을 위해 비모수적 부트스트래핑(Nonparametric bootstrapping) 방법을 활용하기 때문에 정규성 가정에서 자유로우며, CB-SEM에서는 활용할 수 없는 형성적 측정모형을 적용할 수 있다는 장점이 있다(Monecke and Leisch, 2012). 표본크기에 대해서도 일반적으로 30개 이상의 표본을 요구하기 때문에 200개 이상의 표본을 요구하는 CB-SEM에 비해 자유롭다(Shin, 2018). 또한, 요인이 많아 모형이 복잡하거나, 다중공선성을 갖는 경우에도 활용이 가능하다(Jang and Kim, 2012).
PLS-SEM의 평가는 측정모형과 구조모형 평가로 구분되며, 측정모형의 평가는 측정모형이 반영적 지표(Reflective factor)로 구성되었는지 혹은 형성적 지표(Formative factor)로 구성되었는지에 따라 다른 기준을 적용한다. 반영적 측정모형은 내적 일관성 신뢰도(Internal consistency reliability), 집중타당도(Convergent validity), 판별타당도(Discriminant validity) 평가를 진행하며, 형성적 측정모형은 집중타당도, 다중공선성(Multi-collinearity), 외부가중치 및 적재치(Weights and loadings)의 유의성 평가를 진행한다. 구조모형(Structural model)의 경우에는 다중공선성, 경로계수(Path coefficient)의 통계적 유의성, 결정계수(Coefficient of determination), 효과크기(Effect size), 예측적합도(Predictive relevance) 그리고 모형의 전반적인 적합도(Goodness-of-fit)를 평가한다. PLS-SEM의 평가 및 이에 대한 수용 기준은 Table 4와 같다.
Table 4.
Assessment methods and criteria for PLS-SEM
| Assessment method | Acceptance | ||||
| Reflective measurement model | |||||
|
Internal Consistency Reliability |
Cronbach's alpha (Nunnally and Bernstein, 1994) | ≥ 0.6 | |||
|
D-H rho (Dijkstra and Henseler, 2015) | > 0.7 | ||||
|
Composite reliability (Chin, 1998; Henseler et al., 2009) | 0.60 ≤ < 0.95 | ||||
|
Convergent Validity |
Outer loadings (Gefen and Straub, 2005; Hair et al., 2012) | |t| > 1.96, value of loadings should be considered | |||
|
Average variance extracted (AVE) (Fornell and Larcker, 1981) | AVE > 0.5 | ||||
|
Discriminant Validity |
Fornell-Larcker criterion (Fornell and Larcker, 1981) |
Square root of each latent variable should be greater than the highest correlation among the latent variables | |||
|
Cross loadings (Chin, 1998) | Outer loadings should exceed cross loadings | ||||
|
HTMT criterion (Henseler et al., 2015) |
HTMT.85 HTMT < 0.85 |
HTMT.inf not including 1 in the Confidence Interval | |||
| Formative measurement model | |||||
| Convergent Validity |
Redundancy analysis (Chin, 1998) | Path coefficient ≥ 0.7 | |||
| Multi-collinearity |
Variance inflation factor (VIF) (Hair et al., 2016) | External VIF < 5.0 | |||
| Weights, loadings |
Outer weights and loadings (Chin, 1998) | |t| > 1.96, value of loadings should be considered | |||
| Structural model | |||||
| Multi-collinearity |
Variance inflation factor (VIF) (Hair et al., 2016) | Internal VIF < 5.0 | |||
| Path coefficient |
Significance of path coefficient (Henseler et al., 2009) | |t| > 1.96 | |||
| Model fit |
Coefficient of determination (R2) (Cohen, 1988) |
High R2 > 0.26 |
Medium 0.13 < R2 < 0.26 |
Low R2 < 0.13 | |
|
Effect size (f2) (Cohen, 1988) |
High f2 > 0.35 |
Medium 0.15 < f2 < 0.35 |
Low f2 < 0.15 | ||
|
Predictive relevance (Q2) (Stone, 1974; Geisser, 1974) | Q2 > 0 | ||||
|
Goodness-of-fit (Tenenhaus et al., 2005) |
High > 0.36 |
Medium 0.25∼0.36 |
Low 0.10∼0.25 | ||
2.4 연구 가설 및 연구 모형
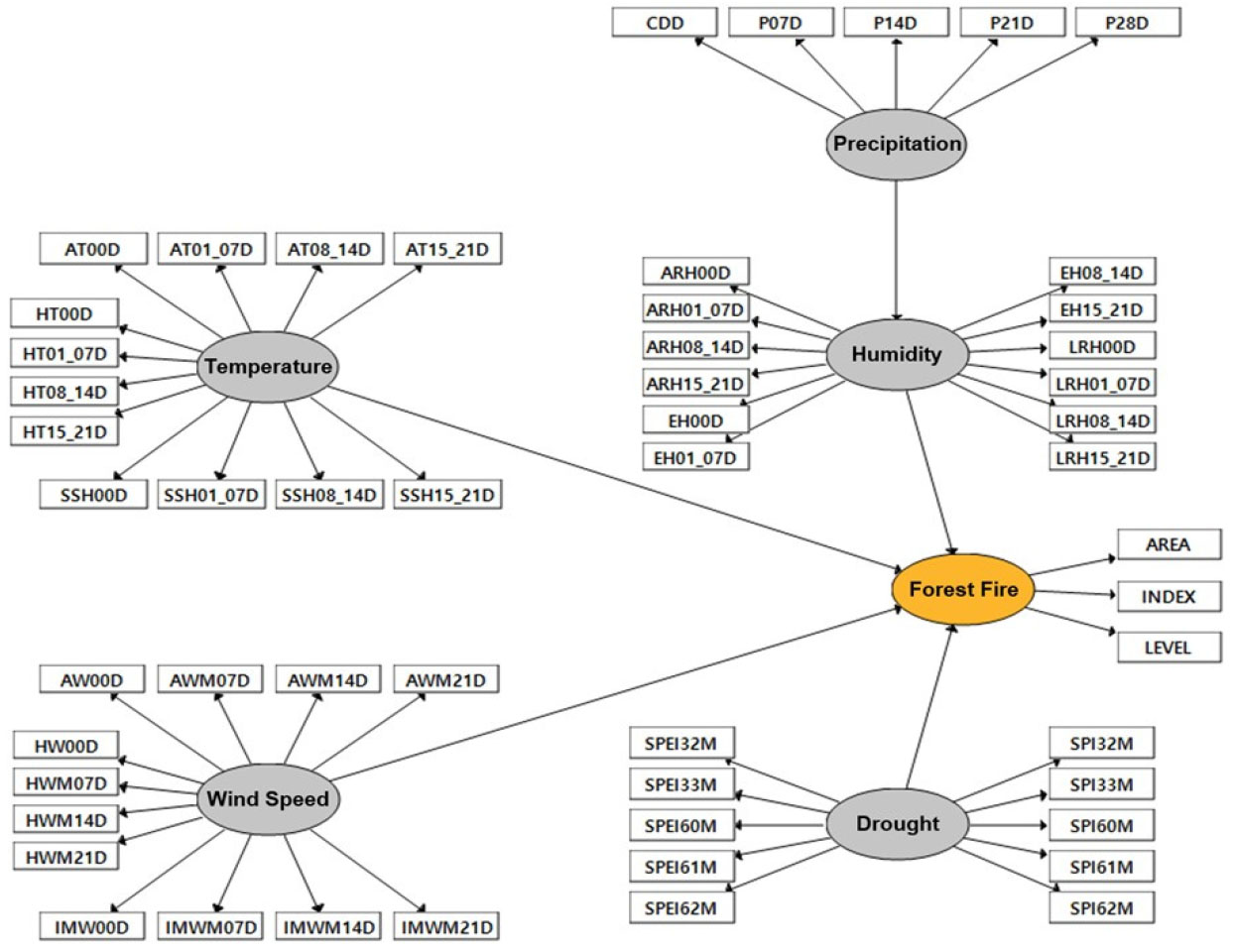
본 연구에서 분석에 활용한 모형은 Fig. 3과 같으며 이에 대한 가설은 다음과 같다.
[H1] 강수는 습도에 정(+)의 영향을 미칠 것이다.
[H2] 습도는 산불 발생에 부(-)의 영향을 미칠 것이다.
[H3] 온도는 산불 발생에 정(+)의 영향을 미칠 것이다.
[H4] 풍속은 산불 발생에 정(+)의 영향을 미칠 것이다.
[H5] 가뭄은 산불 발생에 정(+)의 영향을 미칠 것이다.
[H6] 습도는 강수와 산불 발생 간에 간접영향을 미칠 것이다.
[H6-1] 강수는 습도를 매개로 산불 발생에 부(-)의 영향을 미칠 것이다.
3. 연구 결과
3.1 반영적 측정모형 평가 결과
PLS-SEM의 평가는 측정모형과 구조모형을 구분하여 진행하였다. 먼저 반영적 측정모형에 대해서는 내적 일관성 신뢰도와 집중타당도, 판별타당도 평가를 수행하고, 이를 정리하여 각각 Tables 5 ~ 7에 나타냈다. 내적 일관성 신뢰도의 평가 기준으로는 크론바흐 알파(), D-H rho(), 합성신뢰도()를 활용하며, Table 5에 나타난 바와 같이 본 연구의 모든 잠재변수들은 수용범위를 크게 넘어서지 않으므로 내적 일관성 신뢰도를 확보한 것으로 판단된다.
집중타당도의 평가 기준으로는 탐색적 요인분석(Exploratory Factor Analysis, EFA) 과정의 결과인 외부적재치(Outer loading) 그리고 평균분산추출(Average Variance Extracted, AVE) 값을 활용한다. EFA는 잠재변수와 측정변수를 모두 인과관계로 연결시키며, 여기서 외부적재치는 잠재변수와 반영적 측정변수 간 표준화된 회귀계수를 의미한다. 본 연구의 목표와 내용타당도를 고려하여 산불 피해면적(AREA)을 제외한 외부적재치가 0.4 미만인 측정변수들은 모형 구성 시 제거하였다. Table 5에 나타난 바와 같이 모든 잠재변수들의 AVE가 임계치인 0.5를 넘어서고, Table 6과 같이 대부분의 외부적재치가 수용기준을 넘어서 집중타당도를 확보한 것으로 판단된다.
판별타당도의 평가기준으로는 교차적재치, Fornell-Larcker 기준 그리고 HTMT 기준을 확인하며, Table 4의 기준을 참고하여 Tables 6 and 7을 확인하였을 때 본 연구의 측정모형은 판별타당도를 확보한 것을 확인할 수 있다.
Table 5.
Results of internal consistency reliability and convergent validity assessment
Table 6.
Results of exploratory factor analysis (outer loading)
Table 7.
Results of discriminant validity assessment
3.2 구조모형 평가 결과
본 연구에서 활용한 PLS-SEM의 구조모형에 대한 평가 기준으로 다중공선성, 경로계수의 유의성 그리고 모형적합도가 있다. 먼저 본 연구에서 활용한 잠재변수들의 다중공선성은 내부 분산팽창인자(Variance Inflation Factor, VIF)를 확인하여 판단할 수 있는데, 모든 내생잠재변수들의 내부 VIF값이 5.0 미만으로 잠재변수 간에 다중공선성 문제가 발생하지 않은 것으로 판단된다.
구조모형의 경로계수 유의성은 부트스트래핑을 통해 산출된 표준화된 경로계수의 t-값을 확인하면 판단할 수 있다. t-값이 임계치인 1.96보다 크다면 해당 경로계수가 통계적으로 유의미한 것으로 판단할 수 있다. Table 8에 나타난 바와 같이 본 연구 모형의 구조모형 경로계수는 통계적으로 유의하기 때문에 모든 가설은 채택되었음을 알 수 있다.
구조모형의 적합도를 평가하기 위하여 네 가지의 항목을 확인하였고, 이를 Table 9에 정리하여 제시하였다. 먼저, 결정계수(R2)는 습도와 산불 발생 요인에 대해 각각 0.11, 0.35의 값을 가지므로 Table 4의 기준을 참고하여 Table 9를 확인하였을 때 강수 요인은 습도 요인에 대해 낮은 설명력을, 기온, 습도, 풍속 그리고 가뭄 요인은 산불 발생 요인에 대해 높은 설명력을 가지는 것을 확인할 수 있다. 효과크기(f2)는 습도 요인이 산불 발생 요인에 가장 큰 기여를 하는 것으로 나타났으며, 가뭄과 온도 그리고 풍속 요인 순으로 가뭄에 기여를 하는 것으로 판단된다. 모형의 예측적합도(Q2) 확인 결과 모든 요인은 0 이상의 값을 가져 예측적합도가 있는 것으로 판단된다. 마지막으로 모형의 전반적인 적합도(Goodness-of-fit)의 경우 0.34의 값을 가졌고, Table 4의 기준을 참고하여 Table 9를 확인하였을 때 본 연구의 구조모형은 중간 정도의 적합도를 가진 것으로 판단할 수 있다.
Table 8.
Results of path coefficients assessment
Table 9.
Results of model fitness assessment
4. 결 론
우리나라에서는 기후변화로 인해 건조일수가 증가하고 가뭄 위험이 증가하는 등 산불위험이 지속되고 있으며, 최근 10년 동안 산불 발생건수와 피해면적이 증가하고 있다. 경기도의 산불 발생 및 피해면적 또한 증가 추세에 있으며, 산불 발생은 실제로 기상학적 및 수문학적 요인들과 연관성이 있기 때문에 이를 고려하여 인과관계를 파악할 필요가 있다. 따라서 본 연구에서는 경기도 지역에서 최근 5년간 발생한 산불과 기상학적 및 수문학적 요인 간의 영향 관계를 정량적으로 파악하기 위한 목적으로 PLS-SEM을 활용한 분석을 수행하였으며 이에 대한 결과는 다음과 같다.
본 연구 모형의 측정모형 평가 결과, 내적 일관성 신뢰도와 집중타당도, 판별타당도 확보에 대부분 문제가 없는 것으로 판단된다. 강수 요인의 측정변수 중 연속건조일수(CDD)는 강수 요인의 다른 측정변수들과 부호 방향이 다른데, 이는 음의 상관관계를 갖기 때문이고 이를 통해 습도 요인이 감소하면 연속건조일수(CDD)가 증가하는 것으로 판단할 수 있다. 산불 발생 요인의 측정변수 중 산불 피해면적(AREA)에 대한 외부적재치 값이 수용기준 이하의 값을 가졌고 요인 형성에 있어서 다른 산불 측정변수들과 호응하지 못하였다. 이는 산불위험지수 혹은 위기경보 등급이 높다고 해서 산불 피해면적이 커지는 것은 아니기 때문인 것으로 판단된다. 현재 분석에 활용 가능한 산불 관련 측정변수가 많지 않고 이와 관련된 연구 사례 또한 부족하여 산불 발생 요인의 구성에 한계가 존재하지만, 향후 연구를 통해 산불 관련 변수들이 추가적으로 구축된다면 요인의 형성 측면에서 더욱 적합한 결과를 도출할 수 있을 것으로 판단된다.
구조모형 평가 결과, 다중공선성 문제가 발생하지 않았으며 경로계수의 통계적 유의성 또한 확보되었다. 이를 통해 기상학적 요인인 습도 요인이 산불 발생 요인에 미치는 영향이 -0.42로 가장 컸고, 수문학적 요인인 가뭄, 기상학적 요인인 온도와 풍속 요인 순으로 산불에 각각 0.23, 0.23, 0.15의 영향을 미치는 것으로 파악되었다. 또한, 습도 요인을 매개로 강수 요인이 산불 발생 요인에 -0.14의 간접 영향을 미치는 것으로 확인되었다. 모형적합도 평가 결과 구조모형은 산불에 대해 높은 설명력을 가지며 예측적 적합성을 갖는 것으로 판단된다. 구조모형의 전반적인 적합도는 중간 정도인 0.34의 값을 가지는데, 이를 개선하기 위해 습도 요인에 대해 강수 요인 외 다른 영향요인을 추가하여 모형의 설명력을 높인다면 전반적인 적합도가 상승할 수 있을 것으로 판단된다.
본 연구에서는 측정변수와 잠재변수의 인과 정도를 외부적재치를 통해 정량적으로 나타낼 수 있었으며, 잠재변수 간 직·간접적인 영향을 경로계수를 통해 정량적으로 제시할 수 있었다. 따라서 본 연구의 결과는 경기도 지역의 산불 발생에 대한 영향 요인 및 인과관계를 기존 연구들에 비해 통합적으로 파악할 수 있었다는데 의의가 있다. 또한, 본 연구는 기존의 연구에서 활용되었던 상대습도, 최고기온, 강수량 등의 측정변수들 이외에도 실효습도, 연속건조일수, 가뭄지수, 산불위험지수, 산불 위기경보 등급 등 선행연구들에서 많이 활용되지 않았던 다양한 측정변수들을 분석에 포함시켰으며, 산불 발생일 이전의 영향 또한 고려할 수 있었다는 점에서 유의하다고 판단된다. 따라서 본 연구는 실제 적용가능한 방법으로써 산불 영향요인의 분석과 이에 대한 평가, 그리고, 산불 재난의 대응·대비 계획 수립에 활용될 수 있을 것이다.