1. 서 론

기후변화에 따른 홍수, 가뭄과 같은 극한 기후 현상은 하천 유량의 패턴을 변화시키고, 나아가 댐을 비롯한 수자원 시설의 원활한 운영을 저해한다(Ehsani et al., 2017). 특정 지역에 대해 한정된 시간 동안 발생·지속되는 홍수와 달리, 가뭄은 광범위한 지역에 장기간 발생할 수 있으며, 그 사회·경제적 영향과 피해는 매우 크다(Zhang et al., 2022). UN의 보고서에 따르면, 지난 100년간 전 세계적으로 천만 명 이상이 가뭄으로 인해 사망하였으며, 아프리카 및 아시아 등에서 심각한 경제적 피해가 발생하였다(UN, 2022). 호주의 밀레니엄 가뭄의 경우, 2002년에서 2010년까지 지속되었으며, 이로 인해 국가 농업 생산량이 약 18%가량 감소한 것으로 추산된다(WMO, 2021). 우리나라도 2014년부터 2018년까지 이어진 유례없는 장기 가뭄이 발생하여 전국적으로 농업을 비롯한 많은 분야에 걸쳐 막대한 피해가 발생한 바 있다.

전체 물 이용량의 50% 이상을 댐을 통해 공급하는 우리나라에서(ME, 2024), 가뭄을 예방 및 경감하는데 있어 댐의 역할은 매우 중요하다. 그간 댐을 더 과학적이고 합리적으로 운영하기 위해 많은 기술적 노력이 진행되어 왔지만, 심화되는 기상 이변으로 댐을 안정적으로 운영하는 것은 점점 더 어려워지고 있다(Ehsani et al., 2017). 극심한 가뭄이 지속될 경우, 댐의 저수량이 고갈되어 심각한 수준의 물 공급 재난으로 이어질 가능성이 있다(Karamouz and Araghinejad, 2008). 기후변화에 따라 가뭄은 더 빈번히 발생하고 그 심각성은 더욱 커질 것으로 전망되고 있어, 이에 대비한 적절한 대책이 필요하다(Sheffield et al., 2012). 현재 국내의 댐 용수공급 의사결정은 20년 빈도 갈수 유입 빈도를 기준으로 검토·적용되고 있다. 그러나 이러한 결정론적 방법이 기후 변화로 불확실성이 증가하는 미래 댐 운영 여건에 있어서도 적절할 것인지, 더 나은 방법은 없는지 고민해야 할 필요가 있다. 기후 속에서 댐을 효율적으로 운영하여 가뭄에 따른 피해를 최소화하기 위해서는 신뢰도 있는 중장기적 댐 유입 예측과, 이를 기반으로 한 합리적 용수공급 의사 결정 과정을 구축해 나가야 할 것이다.

중장기적으로 수문상황을 예측하기 위해 국외에서는 계절 기상 전망 기술에 관한 연구 및 적용 노력이 활발히 진행되고 있다(Bauer et al., 2015; Arnal et al., 2018). 계절 기상 전망이란 향후 7개월간 강수, 기온과 같은 기상인자에 대한 앙상블 예측정보를 의미하며, Copernicus Climate Data Store (https://cds.climate.copernicus.eu/)에서는 매월 생산된 전망 정보를 일 단위로 제공한다(Lee et al., 2023b). 최근에는 계절 강수 전망 데이터를 수문 모형의 입력 자료로 하여 계절 유량 전망(Seasonal Flow Forecasts, 이하 SFFs)을 생성하고, 그 결과를 평가하는 연구로 확장되고 있다. SFFs의 예측 성능을 분석한 연구 결과들은 SFFs가 1에서 2개월의 단기간에는 정확도가 높지만, 그 이후에는 성능이 감소하는 경향이 있음을 확인하였다(Yossef et al., 2013; Arnal et al., 2018; Greuell et al., 2018). 국내에서 이를 적용한 연구에서도 이러한 특성이 유사하게 나타난 것으로 확인되었으며, 나아가 SFFs의 성능이 가뭄 시에 더 높아짐을 확인한 바 있다(Lee and Kang, 2024).

유입량에 대한 전망 정보의 개선과 더불어, 이를 활용한 댐의 운영을 최적화하려는 노력도 활발히 진행되고 있다. 구체적으로 이는 최적화하고자 하는 목적함수를 정의하고 Genetic Algorithm (GA), NSGA-II (Nondominated Sorting Genetic Algorithm) 등의 다양한 최적화 알고리즘을 활용하여 최적의 용수공급 스케줄을 찾는 과정을 의미한다(Malekmohammadi et al., 2011; Ni et al., 2022). 현실 세계에 존재하는 대부분의 문제들은 서로 상충되는 여러 개의 목적함수를 가지기 때문에 다중 목적 최적화가 필요하며, 이 경우 최적화의 최종 결과물은 서로 상충하는 여러 목표 간 최적해의 집합(이하 Pareto front)으로 나타난다. 결국 이 집합 중의 하나의 공급 스케줄을 선택하는 의사결정 문제가 발생하는데, 이를 다기준 의사결정 방법(Multi-Criteria Decision-Making, 이하 MCDM)이라고 한다. 최적의 의사결정을 지원하기 위해 Simple Additive Weighting (SAW), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) 등 다양한 기법들이 개발·활용되고 있다(Velasquez and Hester, 2013).

국내에서도 다수의 목적함수를 최적화하여 Pareto front를 생성하고, 최적의 해를 MCMD 기법을 통해 적용한 연구가 진행된 바 있다(Kim et al., 2015; Li et al., 2017, 2018). 이러한 연구는 주로 수리·수문학적 모델링의 최적 매개변수를 추정하는데 적용되었다. 아울러 Ensemble Streamflow Predicition (ESP), 머신 러닝 등을 활용한 앙상블 유입량 예측 기법을 댐 유역에 적용한 연구들도 진행된 바 있지만(e.g. Kang et al., 2014; Jin et al., 2016; Lee et al., 2023a), 대부분 유입량 예측의 정확성에 중점을 두고 있어 실제적인 운영 의사결정까지 확장되지 못했다. 본 연구는 다양한 SFFs를 비롯한 유입 시나리오/전망 조건에서, 다중 목적 최적화를 통해 댐 용수공급 스케줄의 Pareto front를 생성하고, MCDM을 통해 의사결정을 하는 일련의 새로운 댐 운영 방식을 제시한다. 구체적으로, 낙동강 수계 안동-임하댐 및 합천댐에 대해 2014년부터 2018년까지 장기 가뭄 시에 본 댐 운영 방식을 적용·모의하였으며, 그 결과를 바탕으로 본 방식의 가능성과 댐 운영에 미치는 영향을 평가하였다.

2. 연구 대상 및 데이터

2.1 연구 대상

본 연구의 공간적 범위로는 낙동강 유역에 위치하며 이수적인 측면에서 중요성이 높은 안동, 임하 및 합천댐을 선정하였으며, 시간적 범위는 2014년 홍수기 이전(6월 1일)부터 2018년 홍수기 말(9월 30일)까지의 장기 가뭄 기간으로 정의한다. 낙동강 유역에 있는 다목적댐 중에서 남강 및 밀양댐과 같이 홍수 조절이 빈번한 댐과, 저수용량이 작고 최근에 건설된 김천부항, 군위댐 등은 운영자료 부족 등에 따라 금번 연구 대상에서 제외하였다. 본 연구에서는, 도수터널 등을 통해 직·간접적으로 연계 운영하는 안동, 임하댐은 하나의 댐으로 간주하여 평가하였다.

2014~2018년 가뭄은 장기간에 걸쳐 진행되었으며, 댐을 통한 농업, 생활, 공업 및 하천유지 용수의 공급에 큰 어려움을 경험한 바 있다. 분석 기간인 2014년 6월 1일부터 2018년 9월 30일(4년 4개월, 52개월)까지의 전체 누적 유입량은 안동-임하댐의 경우 약 5~10년, 합천댐의 경우 약 5년 수준의 갈수 유입 빈도에 해당하는 것으로 확인되었다. 분석 기간 동안의 댐 저수, 공급 및 수요량 시계열은 Fig. 1과 같다.

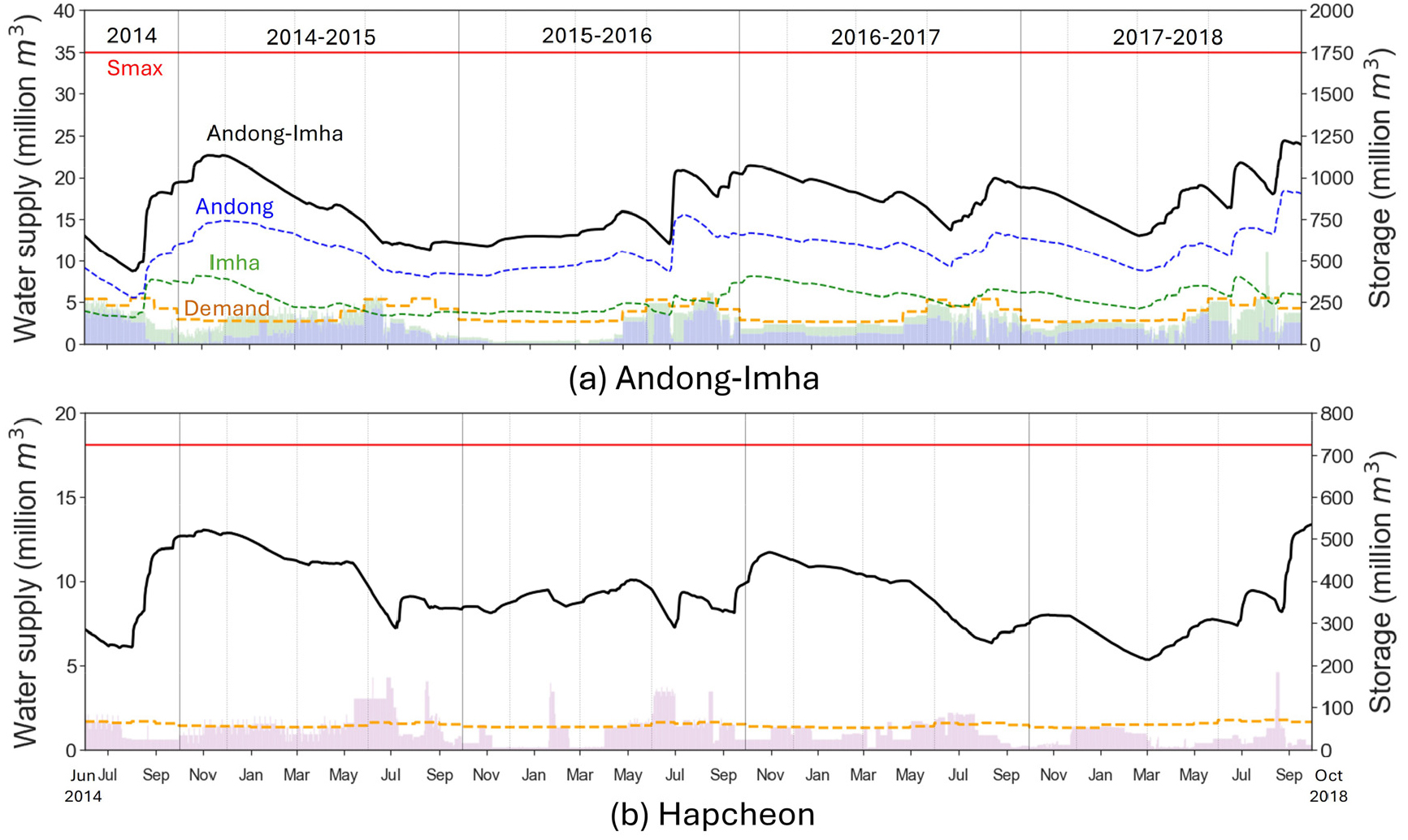
Fig. 1.

Reservoir operation record in Andong-Imha (a) and Hapcheon (b) dam. Black solid line represents the storage volume (million m³) and the bar plot indicate the water supply (million m³) from Andong (blue bar), Imha (green bar) and Hapcheon (purple bar), respectively. Orange dashed line is water demand based on water supply contract of each dam. Smax represents the storage volume at the normal high water level

2.2 데이터

댐의 유입 시나리오를 산정하기 위해 한국수자원공사(K-water)에서 제공하는 유역평균 일 강수 및 유입량 자료를 활용하였다(www.water.or.kr). 또한, ESP의 유입 전망 생산을 위한 수문학적 모형의 입력 자료로는 기상청의 종관기상관측소와 자동관측소의 기온 자료를 활용하였으며, 잠재 증발산량은 기온, 풍속, 일조시간 등을 비롯한 기상관측 자료를 활용하여 Penman-Monteith 기법으로 계산하였다(Allen et al., 1998). 댐 유역의 면적 평균의 수문 데이터를 생산하기 위해 티센방법을 적용하였다.

SFFs 생성을 위해 Copernicus Climate Data Store에서 제공하는 계절 기상(강수, 기온, 증발산량) 전망 정보를 활용하였다. 현재, 다양한 기후 예측 기관들이 계절 기상 전망정보를 Copernicus Climate Data Store 플랫폼을 통해 서비스하고 있지만, 국내에서는 European Centre for Medium-Range Weather Forecasts (ECMWF)에서 제공하는 정보의 예측 퍼포먼스가 가장 높다는 것이 확인된 바 있어(Lee et al., 2023b), 본 연구에는 ECMWF (System 5)에서 제공하는 계절 기상 전망을 활용하였다. Copernicus Climate Data Store에서 제공하는 ECMWF의 계절 기상 전망은 공간적으로 1°×1°의 해상도를 가지고 있으며, 매월 초 향후 1에서 7개월간의 일 단위 예측 정보 앙상블(1993년에서 2016년까지는 25개, 2017년부터 51개 앙상블 제공)을 제공한다. 본 연구에서는 1993년부터 2020년까지 28년간 한반도 지역의 전망 데이터를 내려 받았으며, 이로부터 유역별 면적평균 강수, 기온 및 증발산 전망 시계열 전망 앙상블 데이터를 추출하였다. 계절 기상 전망 정보의 편의 보정을 위해 1993년부터 2010까지의 자료를 관측값과 비교하여 월 단위 편의 보정계수를 산정하는 데 활용하였다.

3. 연구 방법

본 연구에서 적용된 댐 운영 방법은 Fig. 2에 나타난 것과 같이 유입량 시나리오 또는 전망을 선정하고, 최적화를 통한 공급 스케줄의 Pareto front 도출한 후, MCDM 기법들을 적용하여 최종 용수공급 의사결정을 진행하는 방식으로 구성된다(Lee et al., 2024b). 먼저, 매월 향후 총 6개월간의 댐 유입 시나리오 및 전망 정보를 생산하였다(3.1. 유량 시나리오 및 전망 생산). 이 정보를 입력 자료로 하여 최적화 모형을 실행하고 공급 스케줄에 대한 최적해의 집합, 즉 Pareto front를 도출한다(3.2. 댐 용수 공급 스케줄 최적화). 이후, 총 8가지의 MCDM 기법을 통해 Pareto front 중에서 하나의 공급 스케줄을 확정하였으며, 선택된 공급 스케줄과 실제 유입량을 활용하여 댐을 연속적으로 모의운영을 수행하였다(3.3. 다기준 의사결정 방법을 활용한 최적 용수공급 스케줄 선정). 이러한 과정은 2014년 6월 1일의 관측 저수량 조건에서 시작하여, 매월 모의된 저수량을 초기조건으로 하여 2018년 9월 말까지 연속적으로 수행되었다.

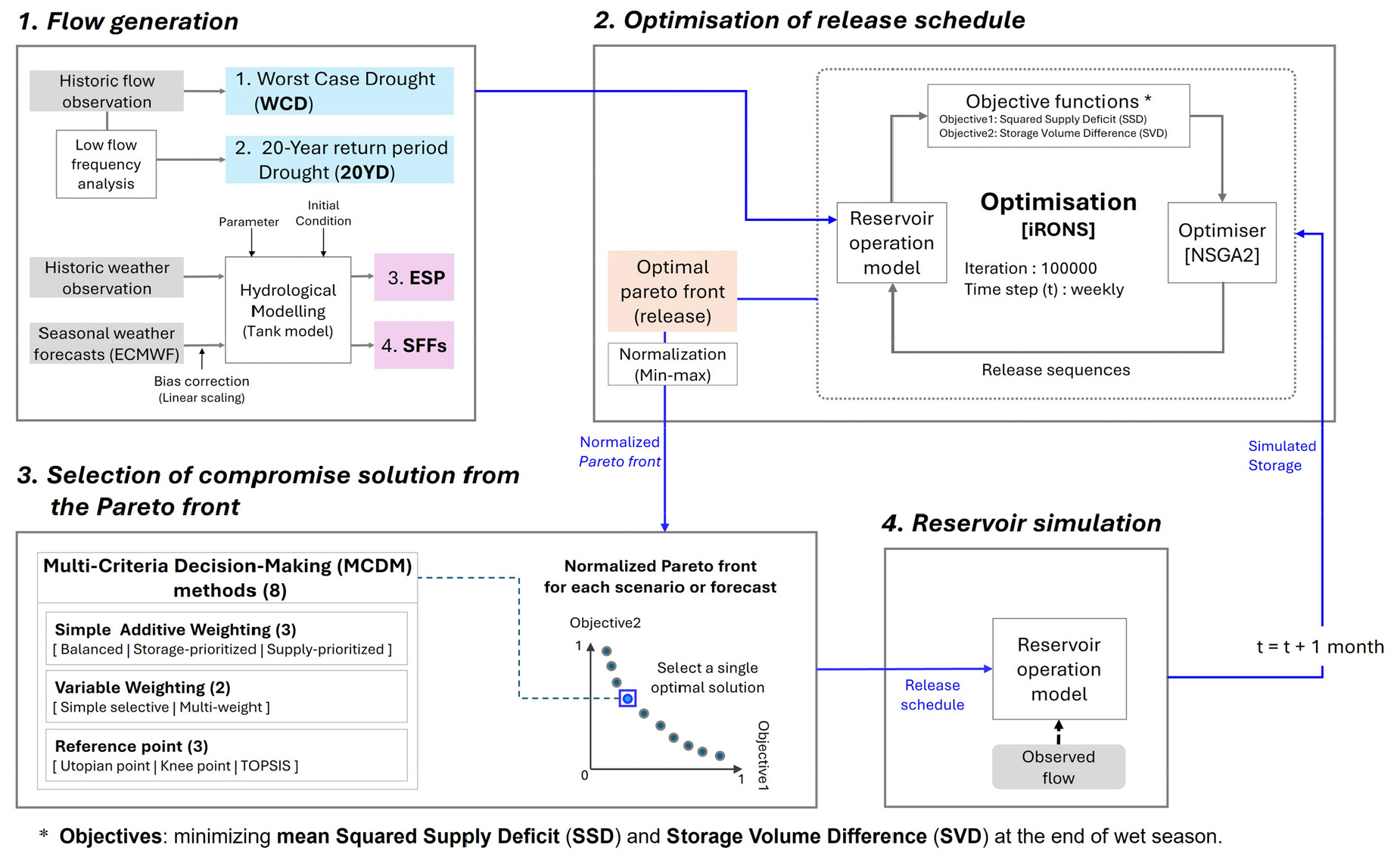
Fig. 2.

Schematic diagram depicting the reservoir simulation process employed in the study (Lee et al., 2024b)

3.1 유량 시나리오 및 전망 생산

본 연구에서는 두 개의 유입 시나리오와 두 개의 전망 정보를 생성·활용하였다. 먼저 유입 시나리오로는, 과거 발생했던 최악의 수문조건을 재현하는 최악 가뭄 시나리오(Worst- Case Drought scenario, WCD)와 20년 빈도 가뭄 유입조건 시나리오(20-Year return period Drought scenario, 20YD)를 각각 활용하였다. 이 두 가지 시나리오는 댐 운영 계획 수립 시 실무적으로 활용되는 방법으로, 현재의 운영 방식에 따른 결과를 의미한다. 구체적으로, 안동-임하댐과 합천댐의 연간 유입량을 분석하여 최저였던 해인 2015년과 2017년의 유입량 자료를 WCD로 활용하였으며, 갈수빈도 해석을 통해 생성된 20년 빈도 유입조건 시나리오(K-water)를 20YD 시나리오로 활용하였다. WCD와 20YD는 하나의 유량 시나리오로 구성되기 때문에 ‘결정론적(Deterministic) 유입 시나리오’라 한다.

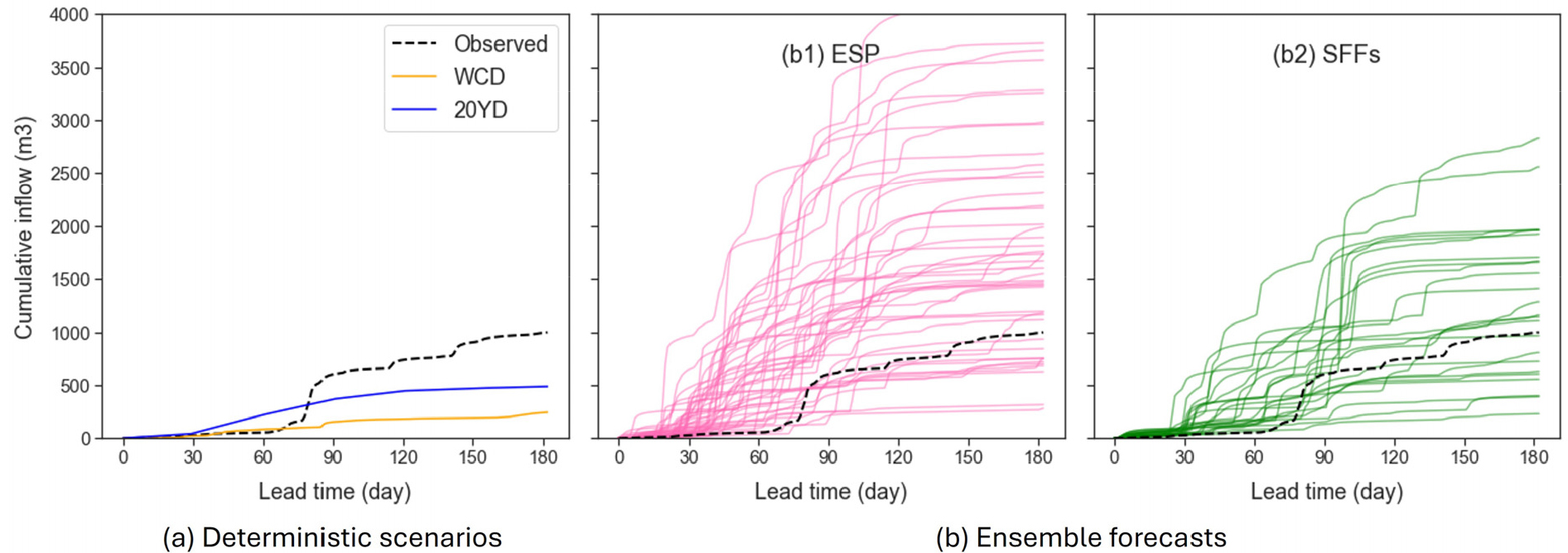
유입 전망 정보로는 국내외 실무에서 많이 활용되는 ESP와 계절 기상 전망을 통해 생성한 SFFs 두 가지를 활용하였다. 먼저, 관측된 강수, 기온 및 Penmann-Monteith 기법을 통해 계산한 잠재증발산량 정보를 Tank 모형의 입력 자료로 구성하여, 1966년부터 2010년까지의 총 45개 ESP 유량 앙상블을 생성하였다(Lee and Kang, 2024). SFFs는 ECMWF에서 제공하는 기상 인자의 앙상블을 조합하여 Tank 모형을 수행하여 생성하였다. SFFs는 General Circulation Models (GCMs)에 의해 특정한 편의를 발생시킬 가능성이 있기 때문에, 과거 실측자료(1993-2010)를 활용하여 선형 편의보정 기법을 통해 계절 기상 전망정보를 보정하였다(Lee et al., 2024a). ESP (45개)와 SFFs (2017년 이전까지 25개, 이후 51개)는 다양한 앙상블로 구성되므로, 이를 ‘앙상블 유입 전망’이라 한다. 결정론적 시나리오(WCD, 20YD)와 앙상블 전망 정보(ESP, SFFs)는 모두 일 단위의 유입량이며, 실제 댐 운영에서와 같이 매월 향후 6개월간의 유입 전망 정보로 구성하였다. Fig. 3은 2014년 6월 기준 안동·임하댐의 누가 유입 정보를 예시로 나타낸다.

Fig. 3.

Example of (a) deterministic scenarios and (b) ensemble forecasts for the Andong-Imha dams in July 2014, projecting the next six months ahead

본 연구에서 수문학적 모델링을 위해 활용된 Tank 모형은 1961년 일본 Sugawara에 의해 개발되어 국내외에 많이 활용되고 있는 개념적 수문 모형이다(Ou et al., 2017; Goodarzi et al., 2020). 본 연구에서는 Tank 모형의 매개변수들을 Shuffled Complex Evolution global optimization algorithm (SCE-UA) 기법을 활용하여 추정(2001-2010) 및 검증(2011-2020) 하고, 그 성능을 Nash-Sutcliffe model Efficiency coefficient (NSE)와 Percentage Bias (PBIAS) 그리고 Ratio of Volume (ROV)를 활용하여 평가 하였다(Lee and Kang, 2024).

3.2 댐 용수 공급 스케줄 최적화

현실 세계에 존재하는 대부분 문제들은 2개 이상의 서로 상충되는 목적함수를 가지며(Zhou et al., 2011), 이러한 문제의 해를 찾는 과정을 다중 목적 최적화라 한다(Wang and Rangaiah, 2017). 이러한 다중 목적 최적화는 댐 운영 최적화 시에도 적용된다. 댐 운영의 기본적인 방향은 저수량은 최대로 확보하되 물 공급 부족은 최소화하는 것으로서, 이들은 서로 상충되는 관계에 있다. 이러한 댐 운영의 방향을 시뮬레이션하기 위해, 본 연구에서는 댐 공급 최적화의 목적함수를 전체 모의 기간 동안 공급 부족량 제곱의 평균인 mean Squared Supply Deficit (SSD)과 저수용량 대비 확보된 저수량의 차를 의미하는 Storage Volume Difference (SVD)로 정의하였다. 여기서, 공급 부족량에 제곱을 한 이유는, 단기간에 발생한 대규모의 공급 부족은 장기간 연속되는 작은 공급 부족과 비교하여 그 영향이 더 크다는 risk hedging의 원리를 반영하기 위함이며, 이러한 방법은 과거 연구에서도 동일하게 적용된 바 있다(Yeh, 1985; Loucks and van Beek, 2017; Peñuela et al., 2020). 목적함수의 계산식은 아래와 같다.

여기서, T는 6개월의 리드타임 동안의 총 주(week)의 수를 의미하며, Smax는 댐의 상시만수위(또는 홍수기 제한수위) 저수량을 의미한다. S는 댐 운영의 목표가 되는 수문년 종료시점인 9월 말의 저수량을 의미하며, d(t)와 Q(t)는 t시간에서의 물 수요와 공급을 각각 나타낸다. SSD와 SVD는 그 값이 적을수록 더 나은 댐 운영을 의미한다. 여기서 목적함수들을 주간단위로 계산하는 것은, 월간 평균 공급량을 산정하는 것 보다 주간단위 공급량을 최적화 하는 것이 실제 운영에 있어 합리적이기 때문이다.

이러한 목적함수를 기반으로, 본 연구에서는 주간 단위 최적 용수공급 스케줄을 비지배 정렬 유전 알고리즘-II (Non-dominated Sorting Genetic Algorithm, 이하 NSGA-II) 기법(Deb et al., 2002)을 활용하여 산정하였다. NSGA-II는 다목적 최적화 문제를 해결하기 위해 개체들을 비지배 관계에 따라 정렬하고, 군집 밀도를 고려하여 다양한 해를 유지하면서 최적해를 찾아내는 유전 알고리즘으로, 다중 목적 최적화를 위해 많이 활용되고 있는 기법이다(Nebro et al., 2022). 이러한 최적화 과정의 결과물은 목적함수(즉, SSD, SVD)를 최소화하는 최적해의 집합이다. 매월 생성된 Pareto front는 100개의 공급 스케줄 옵션(Population size)을 포함하며, 간단하지만 원 데이터의 관계를 잘 보존하는 것으로 알려진 Max-min Normalisation 기법을 통해 표준화하였다(Al Shalabi and Shaaban, 2006).

3.3 다기준 의사결정 방법을 활용한 최적 용수공급 스케줄 선정

3.2절을 통해 총 100가지의 공급 스케줄 옵션을 가지는 Pareto front를 산정하였다. 그러나 실제 댐 운영은 여러 가지 옵션 중에서 하나를 선택하는 과정이 필요하며, 이를 MCDM이라 한다(Malekmohammadi et al., 2011; Ni et al., 2022). 지금까지 다양한 MCDM 기법들이 개발되어 왔으며, 지속적인 연구를 통해 그 퍼포먼스를 테스트하려는 노력이 진행되어 왔다(Velasquez and Hester, 2013).

3.3.1 Simple Additive Weighting

Simple Additive Weighting (SAW) 방법은 가장 일반적이며 많이 활용되는 기본적인 방법이다(Fishburn, 1967). 이는 목적함수에 특정 가중치를 부여하고, 가중치와 목적함수의 곱한 값을 나열하여 최종 옵션을 선택하는 방법이다. 본 연구의 목적함수인 SSD, SVD는 값이 적을수록 더 높은 퍼포먼스를 의미하므로, SAW에 의한 최적 해(Compromise solution, CSSAW)는 아래의 식과 같이 표현된다.

여기서, wSSD와 wSVD는 공급과 저수량 확보에 대응하는 가중치이며, SSDi와 SVDi는 Pareto front에서 1에서 100가지의 옵션 중에서 i번째에 해당하는 옵션을 각각 의미한다. 본 연구에서는 각각 동일한 가중치(wSSD=wSVD=0.5)를 할당하는 Balanced 기법과, 우선시하고자 하는 목적함수에 0.6을 할당하고 다른 목적함수에는 0.4를 할당하는 Storage-prioritized (wSSD=0.4,wSVD=0.6)와 Supply-prioritized (wSSD=0.6, wSVD=0.4)의 총 세 가지 기법을 활용하였다.

3.3.2 Variable Weighting

두 번째로, 저수 상황에 따라 다른 가중치를 할당하는 방법인 Variable Weighting 기법을 적용하였다. 이 기법은 Lee et al. (2024b)이 제안한 방법으로, 댐의 기본 운영 방향을 고려하여 가중치를 다르게 부여하는 기법이다. 즉, 저수량이 풍부할 경우 공급에 집중하고, 적을 경우에는 저수량을 확보하는데 가중치를 두도록 한다. 본 연구에서는 저수량에 따라 앞서 소개한 SAW 방법의 세 가지 기법(Balanced, Storage-prioritized, Supply-prioritized) 중 하나를 선택·적용하도록 하는 Simple Selective 기법과 저수량 구간에 따라 더 세밀하게 가중치를 부여하는 Multi-weighting 기법을 적용하였다. 두 가지 기법 모두 Eq. (3)과 동일하게 표현될 수 있으며, 저수량 구간별 가중치는 Fig. 4와 같이 과거 기간 동안의 저수량을 기반으로 산정·적용하였다.

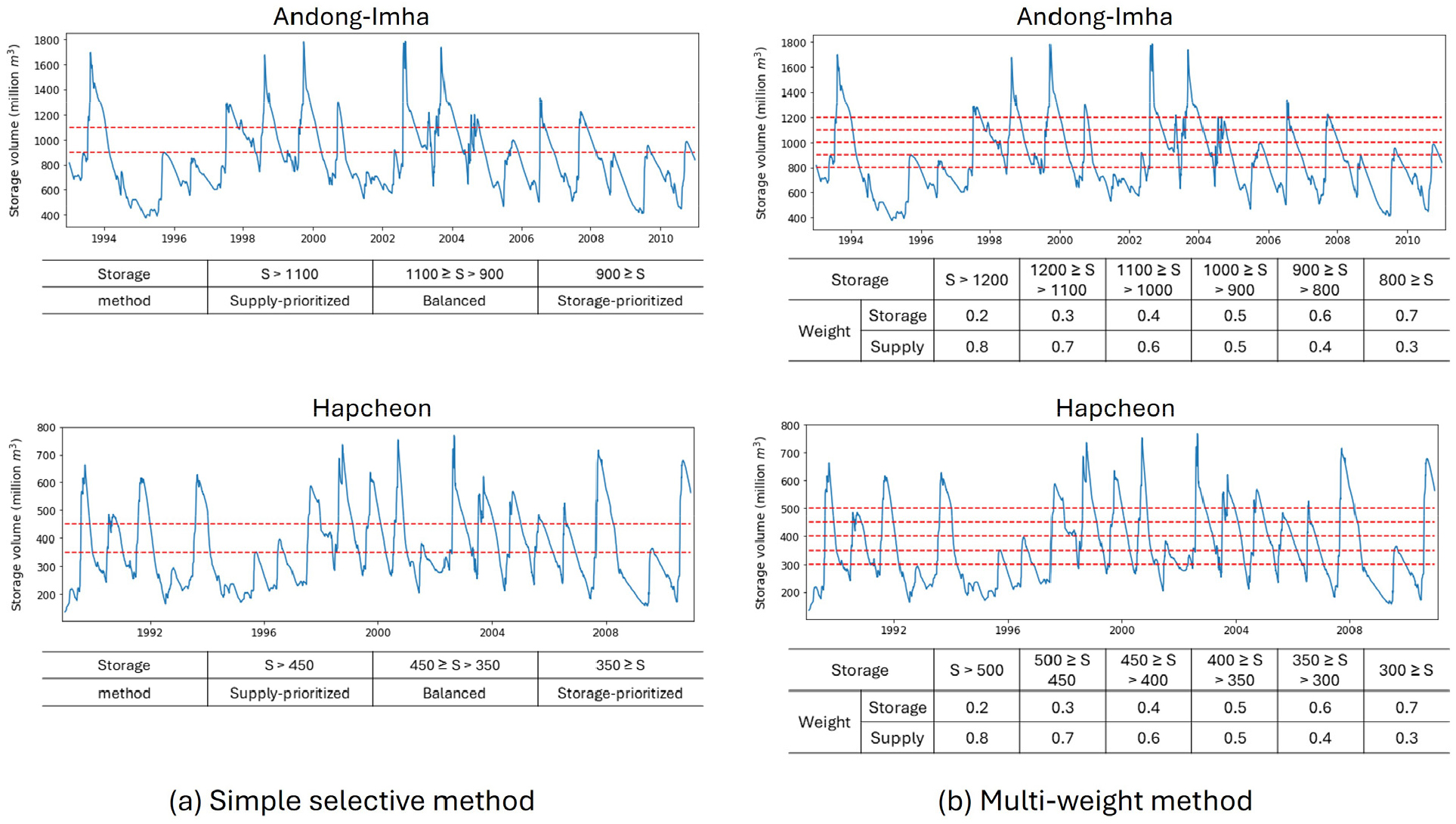
Fig. 4.

(a) Simple selective method: the storage ranges and applied SAW method in each range. (b) Multi-weight method: the storage ranges and applied weight in each range. The blue lines represent the daily reservoir operation records for Andong-Imha (first row) and Hapcheon (second row) reservoir systems

3.3.3 Reference point

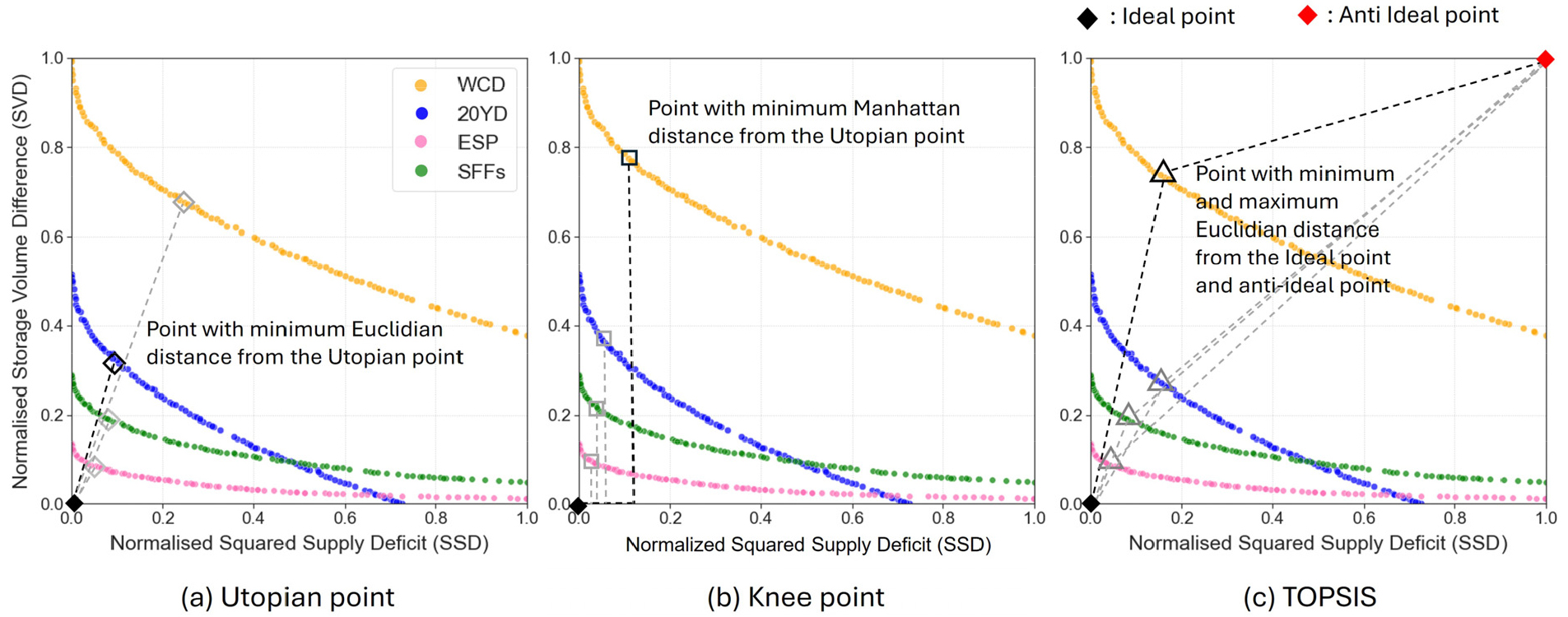
마지막 기법은 3.2절에서 생성한 Pareto front에서 기하학적으로 최적해(용수공급 스케줄)를 선정하는 Reference point 기법이다. 구체적으로 이 방법은 어느 참조 점을 지정하고 그 지점에서 100개에 해당하는 용수공급 옵션까지의 거리를 측정하는 방법으로, 본 연구에서는 Utopian point, Knee point, TOPSIS의 총 3가지 기법을 적용하였으며, 해를 찾는 기하학적 방법은 Fig. 5에 개념적으로 표시한 것과 같다.

Fig. 5에 나타난 것과 같이, Utopian point 기법은 이론적으로 가장 이상적인 Ideal point에서부터 각 옵션까지의 Euclidean distance를 계산하여 그 거리가 가장 적은 옵션을 선택한다(Lu et al., 2011). Knee point는 Pareto front의 곡률이 최대가 되는 지점(knee point)의 옵션을 최적해로 선택하는 기법(Das, 1999)으로, knee point를 찾는 방법 중에서 간단하지만 좋은 퍼포먼스를 나타낸다고 알려진 Minimum Manhattan Distance를 적용하였다(Li et al., 2020). 두 기법은 아래 Eqs. (4) and (5)로 표현된다.

Fig. 5.

An example of the reference point method, including (a) Utopian Point, (b) Knee Point, and (c) TOPSIS method, generated for June 2014 with a 4-month lead time using different flow forecasts (WCD: Yellow, 20YD: Blue, ESP: Pink, SFFs: Green)

여기서, CSUtopian와 CSKnee는 Utopian point 및 Knee point 기법에 의해 제시된 최적의 해을 의미한다. SSDidealpoint와 SVDidealpoint는 각 목적함수의 이론상 가장 이상적인 포인트로 [0, 0]을 뜻한다.

TOPSIS 기법은 Hwang and Yoon (1981)에 의해 제안된 기법으로, United Nations Environmental Program에서 추천하며(Chen, 2000; Zhu et al., 2015), 전 세계적으로 매우 광범위하게 활용되고 있다(Wang and Rangaiah, 2017). 이 기법은 Ideal point (0, 0)와 Anti-ideal point (1, 1)으로 부터의 Euclidean distance를 동시에 고려하며, 아래 식과 같이 표현된다.

여기서, Di+과 Di-은 각각 Ideal 및 Anti-ideal point에서부터 I 번째 옵션까지의 Euclidean distance를 나타낸다. CCi는 i번째 옵션의 Closeness Coefficient로, 가장 큰 CCi를 가지는 옵션이 최적해로 선정된다.

4. 연구 결과 및 고찰

4.1 최적화 반복 횟수가 Pareto front에 미치는 영향 검토

목적함수가 주어져 있을 때(Eqs. (1) and (2)), NSGA-II의 반복 횟수는 Pareto front 생성에 영향을 미칠 수 있다. Fig. 6은 Pareto front 생성 시 NSGA-II의 반복 횟수를 2.5만, 5만, 10만, 20만 회로 모의한 결과를 시기별(2014, 2015, 2016, 2017년 말 기준)로 나타낸 것이다.

Fig. 6(a)에 나타난 바와 같이, 비교적 짧은 시뮬레이션 기간에 대해서는 생성된 Pareto front의 형태가 반복 횟수에 따라 큰 영향을 받지 않았다. 그러나 생성된 Pareto front의 형태의 차이가 누적되고 그에 따른 의사결정이 지속적으로 달라짐에 따라, 즉 Fig. 6(a)에서 6(d)로 시뮬레이션 기간이 늘어날수록 반복 횟수에 따른 Pareto front의 형태의 차이는 더욱 뚜렷이 나타났다. 특히, 반복 횟수가 2.5만 회(검은색 원)로 짧은 경우, Pareto front 형태가 다른 반복 횟수와 매우 다르게 나타난 것을 확인하였는데, 이는 장기간에 대해 Pareto front 생성하기 위해서는 반복 횟수를 증가시킬 필요가 있음을 시사한다.

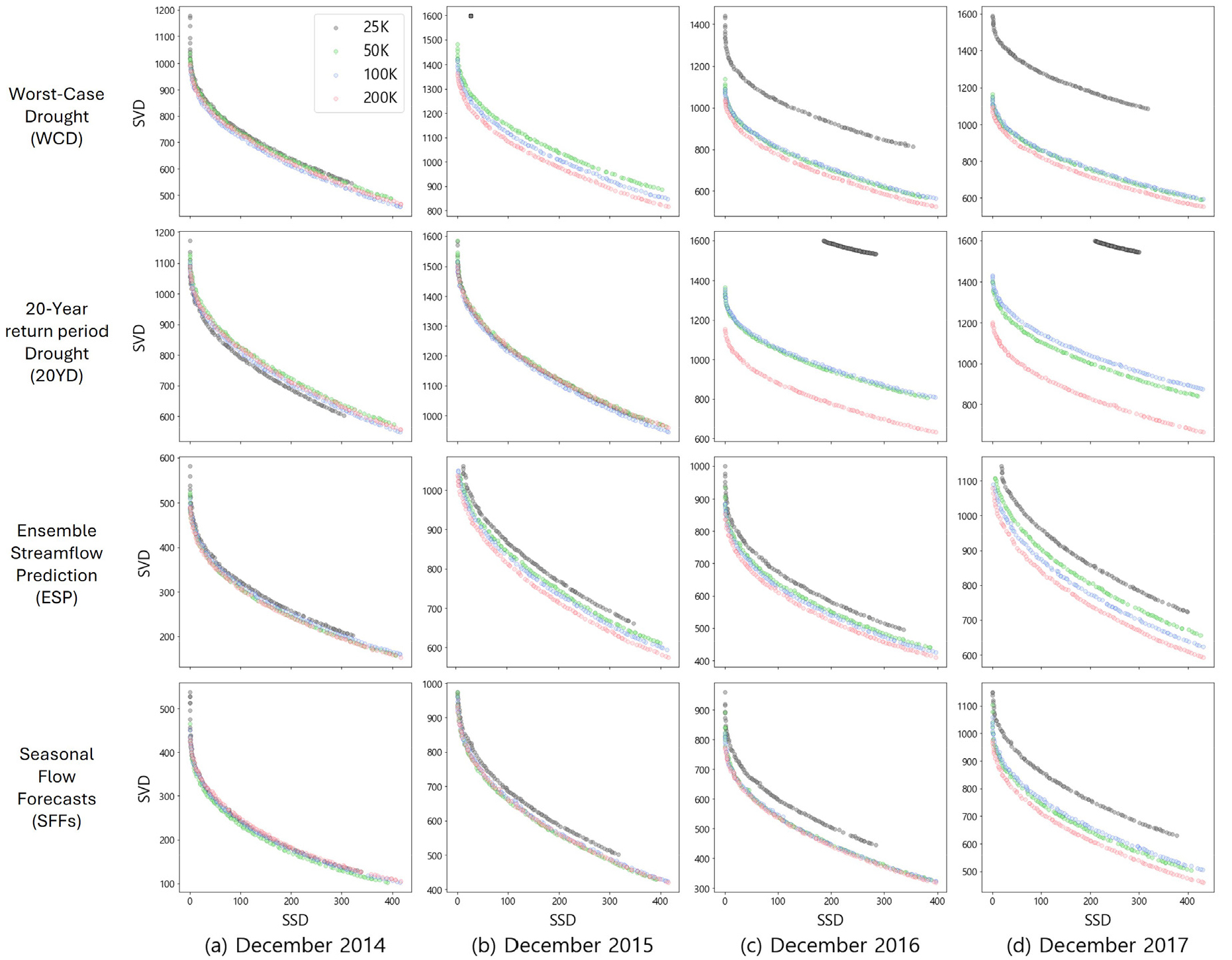
Fig. 6.

Generated Pareto fronts (before Normalization) for Andong-Imha reservoir system under four scenarios/forecasts: Worst-case drought (first row), 20-year return period drought (second row), ESP (third row), and SFFs (fourth row). Each scenario is displayed with varying numbers of iterations (25,000 in black; 50,000 in green; 100,000 in blue; and 200,000 in red circles)

목적함수인 SSD, SVD의 값을 최소화하는 해의 집합을 생성하는 데 있어, 반복 횟수를 증가시킬수록 더 나은 Pareto front를 생성할 수 있다. Fig. 6을 통해 반복 횟수가 많을수록(예를 들어, 20만 회, 빨간색 원) SSD (x축)와 SVD (y축) 모두에서 더 작은 값을 나타내는 것을 확인할 수 있지만, 반복횟수의 증가는 시뮬레이션 소요시간과 비례한다. 따라서 본 연구의 4.2절부터는 Fig. 6에 나타난 결과와 시뮬레이션 소요시간 등을 고려하여, 반복 횟수 10만 회를 통해 생성된 결과들을 기준으로 기술하였다.

4.2 장기 가뭄 시 공급 최적화 결과

2014년 6월부터 2018년 9월까지 안동-임하댐에 대해 향후 6개월의 동안에 대한 4가지 유입 시나리오/전망과 8가지 MCDM 기법을 적용하여 모의운영한 결과는 Fig. 7과 같다.

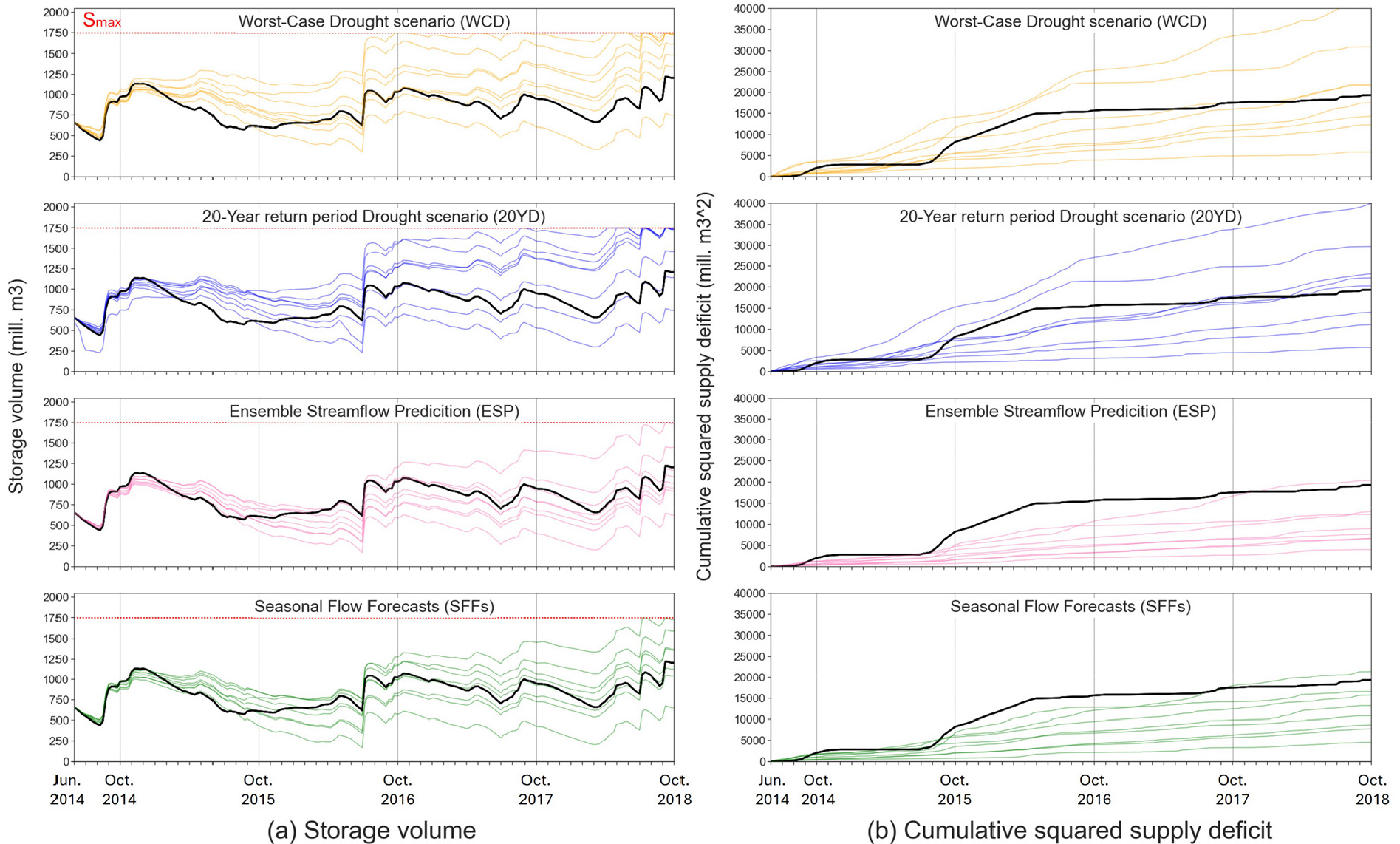
Fig. 7.

Simulated reservoir operation results for Andong-Imha from June 2014 to September 2018 in terms of (a) storage volume and (b) cumulative squared supply deficit. From top to bottom, the rows represent simulation results generated by using WCD (orange), 20YD (blue), ESP (pink) and SFFs (green), respectively. Each sub-figure has 8 simulated results (coloured lines) representing 8 MCDM methods and a single historical operation (black line)

Fig. 7(a)는 4가지 유입 시나리오/전망에 대해 공급 스케줄 최적화 및 다기준 의사결정 모델을 적용하여 모의운영한 저수량을 나타낸다. 결정론적 시나리오(WCD, 20YD)에 의한 모의 결과가 앙상블 전망(ESP, SFFs)을 활용하는 것보다 일반적으로 더 많은 저수량을 확보할 수 있었다. 반면, 공급량의 부족은 결정론적 시나리오를 활용하는 경우에서 더 크게 나타났다(Fig. 7(b)).

Fig. 7의 결과의 해석을 명확하게 나타내기 위해, Fig. 8과 같이 안동-임하댐, 합천댐에 대해 시뮬레이션 종료시점(2018년 9월 말)의 저수량 및 공급 부족량을 box plot을 통해 도시하였다. 여기서 Fig. 8의 첫 번째 열은 확보된 저수량의 범위를 의미하며, 더 큰 값을 가질수록 저수량 확보에 유리함을 나타낸다. 두 번째 열은 누적된 공급부족량(제곱)의 범위를 나타내며, 이는 적을수록 더 나은 댐 운영 결과를 의미한다. 각 그림에 표시된 수평의 검은색 점선은 실제 운영 결과를 나타낸다.

Fig. 8은 안동-임하댐, 합천댐 모두에서 결정론적 시나리오에 의한 모의운영의 결과는 앙상블 전망을 활용하는 경우보다 높은 저수량을 확보하는 데 유리하지만, 공급량의 부족 측면에서는 불리하다는 것을 명확히 나타낸다. 반면, 과거 운영 결과(Historic operation result, 검은색 수평 점선)을 통해 나타난 저수량과 공급 부족을 비교하면, SFFs를 이용한 모의 결과에서 저수량은 과거 운영 결과보다 높게 확보하는 동시에 공급 부족도 줄일 수 있었던 것으로 평가된다. 즉, SFFs를 이용하여 유입을 전망하고, 최적화 운영한 경우가 가장 합리적인 결과를 제시할 수 있다는 것을 의미한다(여기서, 과거 운영 결과는 수계 전체의 연계 운영이 반영된 결과로서, 본 연구에서와 같이 단독으로 운영된 결과와는 차이가 있을 수 있다.).

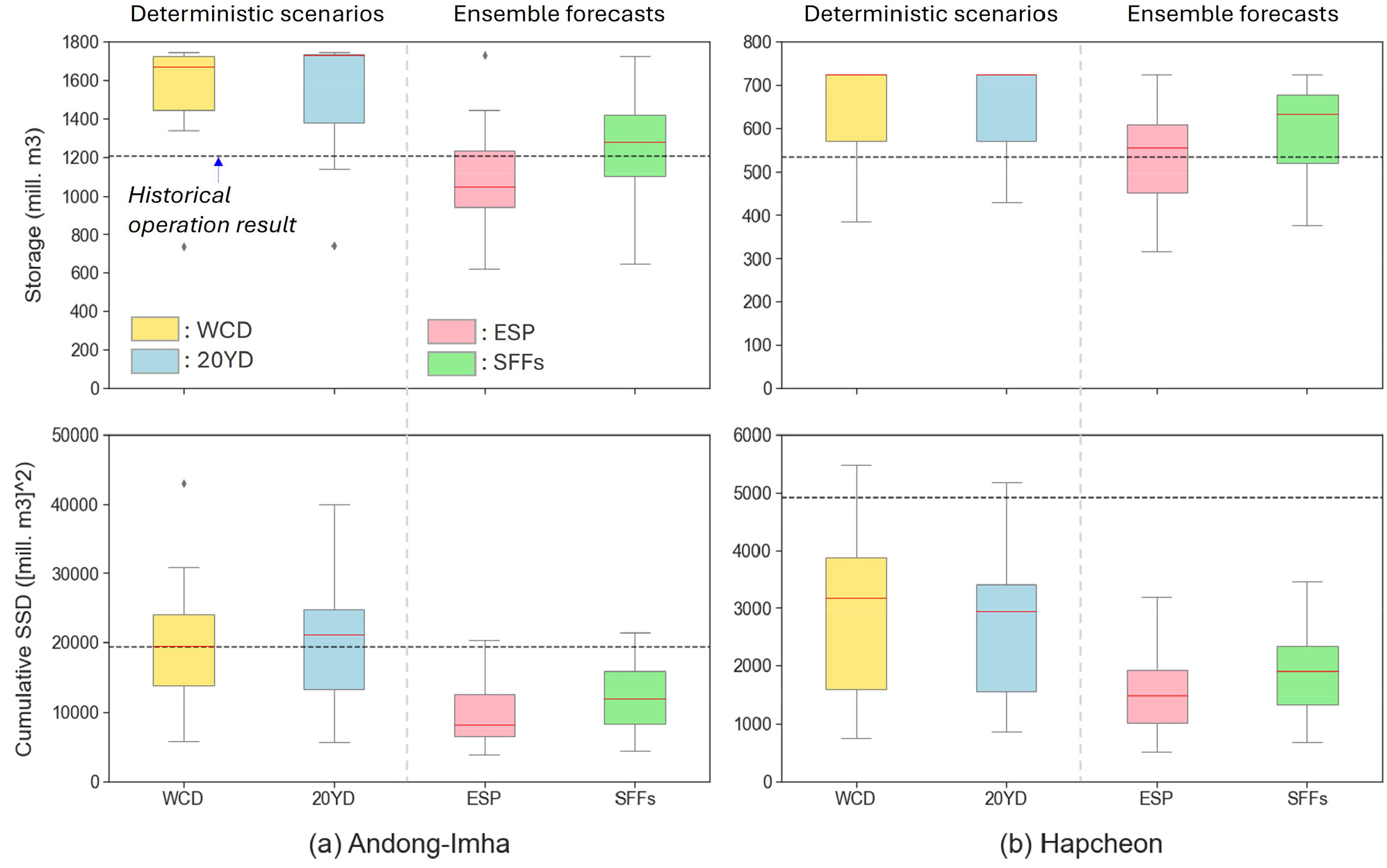
Fig. 8.

Box plot of simulated reservoir operation results for (a) Andong-Imha and (b) Hapcheon at the end of simulation period (September 2018), representing storage volume (first row) and cumulative squared supply deficit (second row) generated using different flow scenarios/ forecasts (WCD (orange), 20YD (blue), ESP (pink) and SFFs (green)). Black dashed horizontal lines show historical operation result

Fig. 8에 나타난 boxplot 종방향 길이는 MCDM 기법에 따라 결정되며, boxplot의 길이가 길수록 의사결정 방법에 따라 더 큰 영향을 받는다는 것을 의미한다. 구체적으로, 저수량 확보 측면에서는(Fig. 8, first row) 앙상블 전망에서, 공급량 최소화 측면에서는(Fig. 8, second row) 결정론적 시나리오에서 MCDM 방법에 의해 댐 운영이 크게 좌우됨을 확인할 수 있다. MCDM은 운영자의 성향을 나타낸다고 볼 때, 동일한 유입 시나리오 또는 전망을 활용하더라도 운영자의 성향에 따라 댐 운영 결과는 크게 달라질 수 있음을 시사한다.

4.3 댐 운영에 미치는 MCDM의 영향 검토

4.2절에서는 각 유량 시나리오/전망에 따라 공급을 최적화하여 모의운영한 결과를 살펴보았다. 본 절에서는 댐 운영자의 의사결정 성향을 시스템적으로 나타내는 MCDM 기법에 따른 댐 운영 결과의 영향을 분석한다. Fig. 9는 각 MCDM 기법(x축)에 따른 저수량과 공급 부족량의 범위(y축)를 boxplot으로 도시한 것이다. 여기서, boxplot의 색은 적용된 총 3가지의 MCDM 방법론을 의미한다.

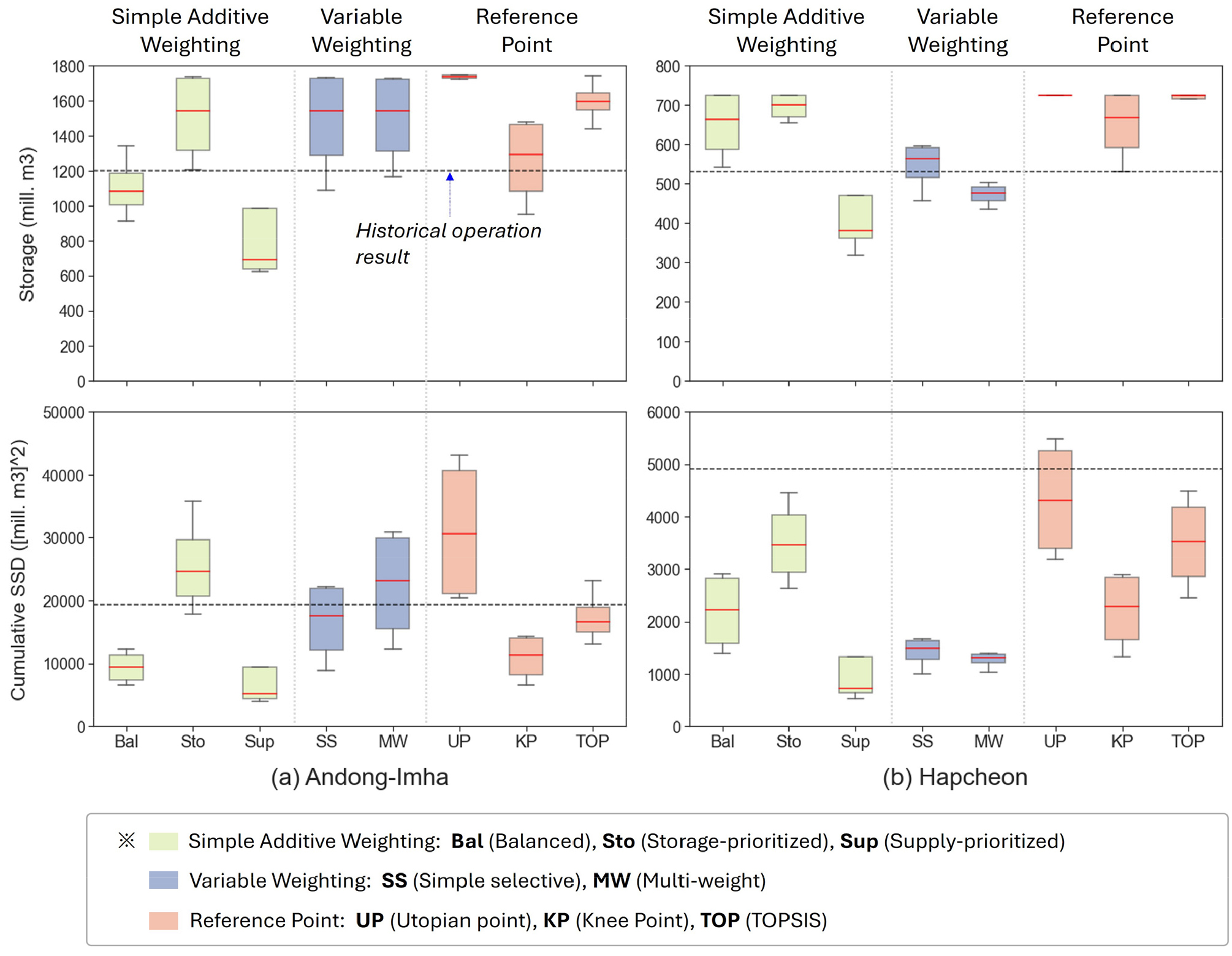
Fig. 9.

Boxplot of simulated reservoir operation results for (a) Andong-Imha and (b) Hapcheon at the end of simulation period (September 2018) representing storage volume (first row) and cumulative squared supply deficit (second row) generated using different MCDM method. Black dashed horizontal lines show historical operation result

Fig. 9에 나타난 바와 같이, SAW 방법(녹색)은 그 가중치에 따른 패턴을 그대로 보여준다. 예를 들어, Storage-prioritized (Sto) 기법은 저수량 확보에 중점을 두어 공급량 부족은 증가한 반면, Supply-prioritized (Sup) 기법은 그 반대의 결과를 나타내었다. 가중치를 저수 상황에 따라 변동하여 적용하는 방식인 Variable Weighting 방법(파란색)은 한쪽 목적함수에 치우치지 않고, 저수량 확보와 공급량 부족 모든 측면에서 전반적으로 합리적인 성능을 나타내었다. Pareto front에서 기하학적 방법으로 최적해를 선정하는 방식인 Reference Point 방법(주황색)의 경우, 그 기법에 따라 뚜렷한 경향성을 보였다. Utopian point (UP) 기법은 저수량 확보에 치중하는 경향을 보이지만, Knee point (KP)와 TOPSIS (TOP) 기법은 더 균형 있는 결과를 제공하는 것으로 나타났다. 과거 운영 결과(검은색 수평 점선)와 비교하면, Knee Point, TOPSIS 기법은 모든 댐 및 목적함수에서 더 나은 운영 퍼포먼스를 나타냈다.

본 연구의 결과만으로 최적의 MCDM 기법을 논하기는 어렵다. 그러나 본 연구를 통해 명확히 확인된 몇 가지 사항을 기술하면 다음과 같다. 첫 번째로, SAW 방법 중 Storage- prioritized나 Supply-prioritized 기법의 경우는 댐 운영에서의 하나의 측면을 강조하므로 사용하는데 주의가 필요하다는 것이다. 그러나 저수량이 공급량에 비해 매우 크거나, 그 반대의 특성을 가진 댐에 대해서는 검토 후 활용이 가능할 수 있을 것으로 판단된다. 둘째, 저수 상황에 따라 가중치를 조절하는 방식인 Variable Weighting 방법은 좋은 성능을 보여주는 것으로 판단되지만, Fig. 4를 통해 가중치를 할당하는 저수량 범위 설정에 따라 운영 결과가 크게 영향을 받을 수 있다. 따라서 과거 운영 관련 자료가 많지 않은 댐에서는 이 방법을 적용하는 데 한계가 있으며, 가중치 할당 및 저수량 범위 설정에 있어 운영자의 주관적 결정에 따라 그 결과에 달라질 수 있다는 단점이 있다. 마지막으로, Reference Point 방법은 Variable Weighting 방법과 달리 기존 운영자료가 없어도 어느 댐에든 적용할 수 있다는 장점이 있다. 아울러, Knee point나 TOPSIS 기법의 경우 그 성과가 과거 운영 결과와 비교 시 매우 높다는 것이 확인되었다. 따라서 신규 댐이나 운영정보가 부족한 경우에는 이 방법을 적용하는 것이 바람직할 것으로 사료된다.

5. 결 론

본 연구는 유입 시나리오/전망을 활용하여 댐을 최적 운영하고, 의사 결정하는 새로운 댐 운영 방법을 제시하고 그 가능성을 과거 가뭄 기간에 대해 적용, 평가하였다. 먼저, 연구의 결과는 Pareto front를 생성하는 데 최적화 알고리즘의 반복 횟수의 중요성을 강조한다. 반복 횟수가 적은 경우(2.5만회), 모의기간이 늘어나면서 Pareto front를 생성하는 데 실패하거나 그 결과가 반복 횟수가 큰 경우와 매우 상이하게 나타났다. 또한, 반복 횟수가 많다는 것은 저수량 확보 및 공급 부족 최소화 측면에서 더 좋은 해를 찾을 가능성이 높기 때문에 모의 시간이 누적될수록 최적화의 효과가 더 뚜렷이 나타났다.

실제 발생한 장기 가뭄에 대해, 본 연구에서 제시한 댐 운영 방식을 적용하여 모의운영 한 결과는 결정론적 시나리오와 앙상블 전망에 따른 명확한 차이를 나타냈다. 즉, 결정론적 시나리오(WCD, 20YD는 유량 시나리오 자체가 매우 건조한 상황을 모방하도록 구성되어 있으며, 그 시나리오가 장기적으로 지속되기 때문에 저수량 확보 위주의 보수적인 운영 결과를 나타냈다. 반면에 건조에서 습윤한 상황까지의 다양한 유입 앙상블을 고려하는 앙상블 전망(ESP, SFFs)을 활용할 경우, 저수량 확보와 용수공급 부족을 동시에 고려하는 운영 결과를 보였으며, 장기 가뭄 시에도 균형 잡힌 운영 결과를 도출할 수 있었다. 특히, 과거 운영 결과와 비교 시, SFFs를 활용한 운영이 가장 우수한 결과를 제시하였다. 또한, 이러한 최적화 운영의 결과는 댐 운영자의 성향을 나타내는 MCDM 기법에 의해서도 크게 영향을 받는 것을 확인하였다.

본 연구를 통해 제시된 댐 운영 방식은 일련의 자동화된 댐 운영 의사결정 방법론으로서 국내외적으로 적용된 사례가 없어 그 결과를 구체적으로 비교·검증하기 어렵다. 또한 대상 가뭄 사상 및 댐이 제한적이기 때문에 본 연구를 통해 일반화된 결론을 도출하는 것은 한계가 있다. 따라서 본 연구를 통해 제시한 결과들을 실제 운영 결과와 비교·검증하는 과정이 중요하며, 이를 위해 다른 가뭄 사상 및 댐들을 대상으로 지속적인 연구를 확대해 나가야 할 것이다. 또한, 댐 운영 최적화 시 목적함수의 결정은 중대한 영향을 미치는 요소이기 때문에, 이에 대해서도 면밀한 검토가 요구된다. 댐별 운영의 목적(수력 발전 극대화, 홍수 리스크 최소화 등)에 맞는 목적 함수를 정의하고 활용한다면, 가뭄 외에도 다양한 분야로의 확대·적용도 가능할 것이다.

기후변화에 따라, 장기 가뭄 등 극한의 이벤트가 증가할 것으로 예측되며(Sheffield et al., 2012), 이로 인해 댐을 안정적으로 운영하는 데 있어 어려움이 가중되고 있다. 이러한 어려움은 댐 운영 의사결정자들의 부담을 가중시키며(Ehsani et al., 2017), 댐 운영의 실패로 이어질 경우 막대한 인명 및 재산의 손실로 이어질 수 있다(Karamouz and Araghinejad, 2008). 따라서 현재 댐을 운영하는 결정론적 방식에 대한 근본적인 고민과 성찰이 필요한 시점이다. 유연하고, 열린 사고를 바탕으로 새로운 기법들을 적극 검토·적용함으로써, 기상 전망에 기반을 둔 선제적 방식으로 댐 운영 시스템을 개선하려는 노력이 지속되어야 할 것이다.