Estimation of fractal dimension for Seolma creek experimental basin on the basis of fractal tree concept

Joo-Cheol Kim; Kwan Sue Jung

doi:10.3741/JKWRA.2021.54.1.49

Preview

Research Article

Journal of Korea Water Resources Association. 31 January 2021. 49-60
https://doi.org/10.3741/JKWRA.2021.54.1.49

Estimation of fractal dimension for Seolma creek experimental basin on the basis of fractal tree concept

Fractal 나무의 개념을 기반으로 한 설마천 시험유역의 Fractal 차원 추정

Joo-Cheol Kim^a

Kwan Sue Jung^b^†

김 주철^a

정 관수^b^†

^aChief Researcher, International Water Resources Research Institute, Chungnam National University, Daejeon, Korea

^bProfessor, Department of Civil Engineering, Chungnam National University, Daejeon, Korea

^a충남대학교 국제수자원연구소 수석연구원

^b충남대학교 토목공학과 교수

^*ksjung@cnu.ac.kr

ABSTRACT

This study presents a methodology to estimate two distinct fractal dimensions of natural river basin by using fractal tree concept. To this end, an analysis is performed on fractal features of a complete drainage network which consists of all possible drainage paths within a river basin based on the growth process of fractal tree. The growth process of fractal tree would occur only within the limited drainage paths possessing stream flow features in a river basin. In the case of small river basin, the bifurcation process of network is more sensitive to the growth step of fractal tree than the meandering process of stream segment, so that various bifurcation structures could be generated in a single network. Therefore, fractal dimension of network structure for small river basin should be estimated in the form of a range not a single figure. Furthermore, the network structures with fractal tree from this study might be more useful information than stream networks from a topographic or digital map for analysis of drainage structure on small river basin.

Keywords

Fractal tree

Horton’s law of drainage composition

Network

Bifurcation

Small river basin

본 연구에서는 Fractal 나무의 개념을 이용하여 자연유역의 두 가지 개별적 Fractal 차원을 추정하는 방법을 제시하고자 한다. 이를 위하여 Fractal 나무의 성장 과정을 기반으로 유역 내부에서 발생 가능한 모든 배수 경로를 추출하여 완전한 배수망을 구성하고 이에 해당하는 Fractal 특성을 분석해 보고자 한다. 유역 내부에서 Fractal 나무의 성장 과정은 하천 유동의 특성을 가지는 배수 경로에서만 제한적으로 나타날 수 있다. 소규모 유역의 경우 Fractal 나무의 성장 단계에 따라 망상 구조의 분기 특성이 단일 하천 구간의 사행 특성에 비하여 민감하게 변화하여 단일한 망상 구조 속에서도 다양한 분기 구조가 생성될 수 있다. 따라서 소규모 유역을 대상으로 한 망상 구조에 대한 Fractal 차원은 단일한 수치의 고정된 형태보다는 범위의 형태로 취급되어야 하는 것이 타당한 것으로 판단된다. 또한, 소규모 유역의 배수 구조에 대한 분석에는 지형도나 수치지도로부터 추출한 하천망보다 본 연구에서 제시한 Fractal 나무의 성장에 따른 망상 구조와 같은 정보가 더 유용할 수 있을 것으로 판단된다.

키워드

Fractal 나무

Horton의 배수 구성 법칙

망상 구조

분기

소유역

MAIN

1. 서 론
2. 이론적 배경
2.1 Horton의 배수 구성 법칙
2.2 유역의 Scaling 법칙
2.3 Fractal 나무
3. 방법론
3.1 대상 유역
3.2 지형분석
3.3 Fractal 차원의 산정
4. 적용사례
4.1 Fractal 나무의 구성
4.2 망상 구조의 Fractal 차원
4.3 Hack의 법칙
4.4 Horton 비
5. 결 론

1. 서 론

Fractal 기하학(Mandelbrot, 1982)은 표준 기하학만으로는 설명이 불가능한 복잡한 자연현상들에 대한 체계적인 접근 수단 중의 하나로 등장하였다. 자연현상이 갖는 복잡성(complexity)에 대한 원형(prototype)으로 과거 수문학자들이 경험적으로 찾아낸 바 있는 유역의 거동 특성(예를 들면, Horton의 배수 구성 법칙(Horton, 1945)이나 Hack의 법칙(Hack, 1957) 등)에 주목하였는데 이는 유역이 무수히 많은 성분들의 동적(dynamic) 상호작용으로 구성되는 대표적인 복잡계(complex system) 중의 하나임을 증명하는 것으로 볼 수 있을 것이다(Kim and Kim, 2008). 실제로 유역은 지표면과 하천 사이의 상호작용을 통하여 강우로 인한 유입량을 효율적으로 배수하기 위하여 끊임없이 진화하고 있는 자연계의 일종으로서 이러한 유역의 점진적인 변화과정 속에는 거시적인 규모의 지질구조학적 융기(tectonic uplift)로부터 유수(流水)에 의한 국부적인 세굴(fluvial erosion)에 이르기까지 수많은 현상들의 복잡한 상호작용들이 포함된다.

지리정보체계(Geographic Information System, GIS)의 발달은 과거 지형도 상에서는 시도조차 할 수 없었던 다양한 지형 인자들의 추출(Moussa, 2003)과 함께 유역의 형상(shape)에 대한 새로운 방식의 접근을 가능케 하고 있다. 특히, O’Callaghan and Mark (1984)가 하천을 형성하기 위한 한계지지면적의 개념을 제시한 이래 DEM (Digital Elevation Model)을 이용하여 하천망(stream network)을 모의하기 위한 다양한 모형들이 제시되어 오고 있다(Tarboton et al., 1992; Montgomery and Foufoula-Georgiou, 1993; Ijjasz-Vasquez and Bras, 1995; Tarboton, 2003). 현재 이러한 기술적 진보는 하천망의 공간 채움(space filling) 구조를 정량적으로 계량할 수 있는 수준에까지 이르고 있는바, 대표적인 예로서 Tarboton et al. (1988)은 DEM으로부터 추출한 하천망에 대하여 Richardson의 방법 및 box counting 방법 등을 적용하여 Fractal 차원(dimension)을 추정한 바 있다. 여기서 Fractal 차원이란 자기 상사성(self-similarity)의 원리에 따라 정의되는 분수 형태의 차원(Yang and Paik, 2017)을 의미하는 것으로서 이들은 자연유역의 하천망은 개별 하천 구간과 망상(network) 구조로서의 하천망이 별개의 차원을 갖는 Fractal 도형의 일종임을 제시한다. 비슷한 시기에 La Barbera and Rosso (1989) 및 Rosso et al. (1991)은 하천망의 Fractal 차원에 대한 관계식을 Horton의 배수 구성 법칙과 결합된 형태로 발표한다. 이후 이들의 연구결과를 바탕으로 DEM을 기반으로 한 하천망의 Fractal 차원과 Horton의 배수 구성 법칙에 대한 일련의 연구 성과들이 발표되어 진다(Beer and Borgas, 1993; Moussa and Bocquillon, 1996; Puente and Castillo, 1996). 주목할 만한 연구 성과로서 Agnese et al. (1996)은 하천망의 Fractal 차원을 Shreve (1966)의 수로 구간(link) 분류법에 따라 수계망 크기(magnitude)의 함수로서 제시한 바 있는데, 이는 전술한 Horton의 배수 구성 법칙을 기반으로 한 연구 성과들과 더불어 경험적인 지형 법칙과 Fractal 기하학을 결합하여 하천망의 구조에 대한 일반 이론을 수립하고자 한 수문학자들의 혁신적인 시도로 평가할 만 하다(Kim and Kim, 2008). 한편, Peckham (1995)과 Tarboton (1996)은 Tokunaga의 법칙(Tokunaga, 1966)에 대한 해석적 접근을 통하여 하천망의 Fractal 차원에 대한 관계식을 해당 하천망의 측면분기 구조를 기반으로 제시하였다. 또한 Dodds and Rothman (2000)은 개별 하천 구간의 Fractal 차원과 Hack의 지수를 기반으로 망상구조를 구분할 수 있음을 주장하였는데 주요한 지형 법칙들이 전술한 두 지형 인자의 함수 형태로 나타낼 수 있음을 제시하였다. 특히 Yang and Paik (2017)은 Fractal 차원을 하천망의 형태를 특성화할 수 있는 배수 구조에 대한 척도로서 강조하였다.

Kim and Kim (2008)과 Kim and Jung (2015)은 Fractal 나무(Fractal tree)의 개념을 이용하여 자연유역의 Fractal 차원을 추정하는 방법을 개발하고자 하였다. Fractal 나무는 자기 상사성의 원리에 따라 성장하는 Fractal 도형의 일종으로서 선(線)으로 이루어진 개체가 분기(bifurcation) 현상을 통해 면(面)을 채워가는 과정에 대한 논리적 틀을 제공한다. Newman et al. (1997)은 자연유역의 하천망은 측면분기 구조를 갖는 Fractal 나무의 일종으로서 특히 Tokunaga의 법칙(Tokunaga, 1966)에 따라 측방지류의 분기비가 일정한 Fractal 나무를 Tokunaga 나무로 분류한 바 있다. 이에 따라 Kim and Kim (2008)과 Kim and Jung (2015)은 Fractal 나무와 하천망의 형태를 동일한 구조로 가정하여 망상 구조의 분기 특성에 접근하고자 하였다. 하지만 이들의 연구는 주로 하천망이 가지는 망상 구조에만 집중되었기 때문에 단일 하천 구간의 사행(meandering) 특성에 대한 접근이 이루어지지 않았다. 본 연구의 목적은 이러한 선행 연구가 가지는 단점을 보완하여 하천망의 구조에 내재한 두 가지 개별적 Fractal 차원을 Fractal 나무의 틀 내에서 동시에 평가할 수 있는 방법론을 제시해보고자 하는 것이다. 특히 본 연구에서는 대부분의 지형 법칙들이 가지는 특징 중의 하나인 점근적(asymptotic) 타당성, 즉 유역의 규모가 커질수록 보다 타당한 결과를 줄 수 있다는 가정사항을 소유역을 대상으로 시험하여 중소규모의 유역을 대상으로 한 우리나라 대부분의 수문학적 실무에 있어 하천망의 Fractal 차원에 대한 개념을 유용하게 이용할 수 있는 기초를 제공하고자 한다.

여기서 한 가지 고려해야 할 사항으로 분석에 이용할 하천망의 공간적 범위를 들 수 있다. 이와 관련한 선행 연구로서 Kim and Kim (2007)은 DEM으로부터 신뢰성 있는 하천망을 추출하기 위한 연구를 수행한 바 있다. 이들이 제시한 주요한 결론 중의 하나는 하천망의 동정(identification)에 사용되는 방법에 따라 단일 유역에 대해서도 다수의 하천망이 수집될 수 있다는 점이다. 실제로 이들은 자신들의 연구 과정을 통하여 총 4개의 하천망을 획득하였는데, 이는 국립지리원에서 발행한 수치지도 상의 하천망, 수자원 단위지도 상의 하천망 그리고 이들이 면적한계기준(O’Callaghan and Mark, 1984)과 경사-면적한계기준(Ijjasz-Vasquez and Bras, 1995)을 적용하여 DEM으로부터 직접 추출한 2개의 하천망들로 구성된다. 이들 4개의 하천망은 서로 완전히 일치하지는 않지만 시각적으로 유사한 형상을 공유하고 있으며 각 하천망들 사이의 가장 큰 차이점은 유원(source) 면적의 규모에서 찾을 수 있었다. 유원 면적은 유역의 임의 지점을 하천과 지표면으로 구분하는 기준으로서 이에 따라 동일한 유역에 대하여 촘촘한 형태의 하천망이나 성긴 하천망을 추출할 수 있게 된다. 하지만 아직까지 유원 면적에 대한 이론적 혹은 정량적 정의는 제시되지 않고 있다. 이에 따라 이들은 “유역 내 존재하는 배수 경로를 하천과 지표면을 구분하지 않고 모두 도시해 볼 경우, 하천망과 지표면의 상이한 특성을 발견할 수 있을 것인가?” 하는 질문을 던진 바 있다. 따라서 본 연구에서는 이들의 접근법에 따라 유역 내부에서 발생할 수 있는 모든 배수 경로들을 하나의 도상에 도시하고 이로부터 해당 유역에 대한 완전한 배수망(drainage network)을 구성하여 이에 대한 기하학적 특성을 Fractal 차원을 기반으로 분석해 보고자 한다.

2. 이론적 배경

2.1 Horton의 배수 구성 법칙

하천망의 위상 구조(topology)를 규정하는 Strahler의 차수 기법은 다음과 같이 기술될 수 있다(Smart, 1972).

① 수원(source)으로부터 발원한 하천은 1차 하천으로 정의된다.

② 두 개의 $ω$ 차 하천이 만나면 합류점(confluence) 직하류에는 $ω + 1$ 차 하천이 생성된다.

③ 서로 다른 차수의 두 하천이 만나면 합류점 직하류 구간은 두 개 차수 가운데 큰 차수를 유지한다.

상기한 Strahler의 차수 기법에 따라 하천망의 분기비 R_B, 길이비 R_L 그리고 면적비 R_A는 아래와 같이 정의된다.

(1)

R_{B} = \frac{N_{ω - 1}}{N_{ω}}

(2)

R_{L} = \frac{L_{ω}}{L_{ω - 1}}

(3)

R_{A} = \frac{A_{ω}}{A_{ω - 1}}

여기서 $N_{ω}$ , $L_{ω}$ , $A_{ω}$ 는 각각 $ω$ 차 하천의 개수, 평균 길이 및 평균 배수 면적이다. Horton (1945)은 단일 하천망의 경우 Eqs. (1) and (2)의 R_B와 R_L은 $ω$ 와 무관하게 일정한 값을 가짐을 제안하였다. 이후 Schumm (1956)이 Eq. (3)의 R_A 역시 유사한 거동을 보임을 제시함에 따라 Eqs. (1) ~ (3)을 Horton의 배수 구성 법칙으로 통칭하고 있다.

2.2 유역의 Scaling 법칙

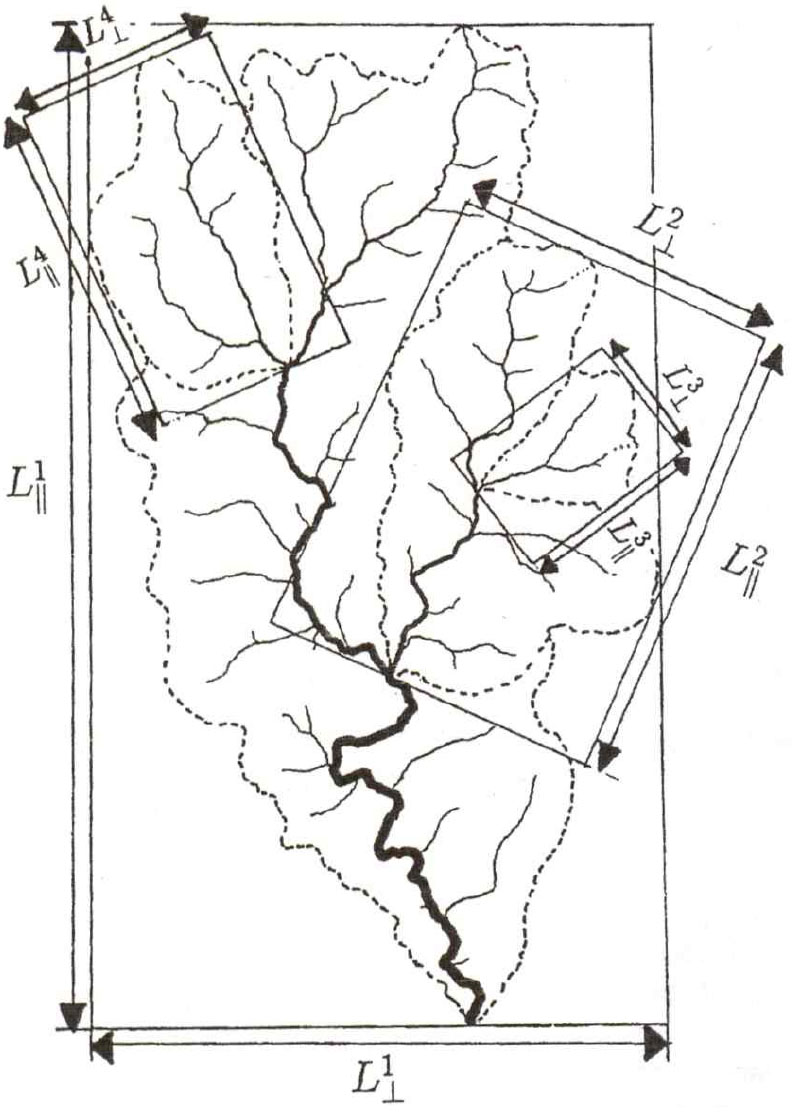
Fig. 1에 도시한 바와 같이 자연유역의 집수평면(catchment planform)을 외접하는 직사각형의 길이와 폭을 각각 $L_{∥}$ 과 $L_{⊥}$ ( $L_{∥} > L_{⊥}$ )라 할 경우, 해당 유역의 배수 면적 A는 다음과 같은 비례식의 관계를 갖는다(Maritan et al., 1996; Dodds and Rothman, 2000).

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F1.jpg

Fig. 1

Catchment planform

(4)

A \propto L_{∥} L_{⊥}

여기서 유역의 평면 형상이 갖는 이방성(anisotropic) 성장 특성을 고려할 경우, $L_{⊥}$ 과 A에 대한 scaling 법칙을 $L_{∥}$ 의 함수형태로 나타낼 수 있게 된다.

(5)

L_{⊥} \propto L_{∥}^{H}

(6)

A \propto L_{∥}^{1 + H}

여기서 H는 Hurst 지수이다. 또한, 단일한 하천 구간의 길이 L이 갖는 사행 특성 역시 Eq. (5)나 Eq. (6)과 유사한 형태의 scaling 법칙에 따라 다음과 같이 나타낼 수 있다(Hergarten, 2002).

(7)

L \propto L_{∥}^{d_{L}}

여기서 d_L은 단일한 하천 구간의 Fractal 차원이다.

만약 Eq. (7)의 관계를 Eq. (6)에 대입할 경우 다음과 같이 자연유역의 형태를 대표하는 경험 법칙 중의 하나인 Hack의 법칙을 유도할 수 있게 된다(Kim and Lee, 2009).

(8)

L \propto A^{h}; h = \frac{d_{L}}{1 + H}

여기서 h는 Hack의 지수이다. Rosso et al. (1991)은 Eq. (8)의 L과 A를 Eqs. (2) and (3)을 기 반으로 치환하고 고려하는 유역의 차수 $Ω$ 에 극한을 취하여 d_L에 대한 관계식을 아래와 같이 Horton 비의 함수형태로 나타낸 바 있다.

(9)

d_{L} = (1 + H) \frac{\ln R_{L}}{\ln R_{A}}

여기서 한 가지 주지할 사항은 이들이 본래 제시한 관계식의 경우 Eq. (9) 우변의 H가 1로 고정되어 있다는 점이다. 이는 Mandelbrot (1982)의 접근법과 유사하게 유역의 평면 형상을 등방성(isotropic) 도형으로 간주함에 기인하는 것으로, 이에 따라 Eq. (9)는 원형 관계식(Rosso et al., 1991)에 비하여 보다 일반화된 형태의 d_L에 대한 관계식으로 평가될 수 있다.

2.3 Fractal 나무

분기 현상에 따른 하천망의 형태적 특성은 Fig. 2에 도시한 Fractal 나무의 성장 과정에 대한 이론적 고찰로부터 추론될 수 있다(Hergarten, 2002; Kim and Kim, 2008; Kim and Jung, 2015): 단위 길이를 갖는 Fractal 나무 한 그루의 몸통(trunk)을 고려하여 본다. 만약 각 성장 단계별로 길이가 $λ$ 배( $0 < λ < 1$ ) 만큼 축소된 가지(branch)가 n개씩 분기할 경우, k번째 성장 단계에서 분기하는 가지의 개수 n_k와 그 길이 r_k는 다음과 같이 나타낼 수 있다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F2.jpg

Fig. 2

Fractal tree

(10)

n_{k} = n^{k}

(11)

r_{k} = λ^{k}

여기서 길이가 r_k보다 크거나 같은 가지들의 개수 N(r_k)는 다음과 같이 등비급수의 합을 이용하여 산정할 수 있게 된다.

(12)

N (r_{k}) = \sum_{i = 0}^{k} n^{i} = \frac{n^{k + 1} - 1}{n - 1}

이에 따라 Eqs. (10) and (11)의 관계를 Eq. (12)에 대입하여 정리하면 해당 관계는 다음과 같이 변환된다.

(13)

N (r_{k}) = \frac{n}{n - 1} r_{k}^{\frac{\ln n}{\ln λ}} - \frac{1}{n - 1}

여기서 Eq. (13) 우변의 $\frac{\ln n}{\ln λ} = - d_{N}$ 로 치환할 경우, 다음과 같은 멱함수 법칙분포(power law distribution)의 관계를 유도할 수 있게 된다.

(14)

N (r_{k}) \propto r_{k}^{- d_{N}}

Eq. (14) 우변의 d_N은 Fig. 2에 도시한 Fractal 나무의 Fractal 차원을 정의하는 것으로, 단일한 하천구간의 사행 특성을 계량하는 Eq. (7)이나 Eq. (9)의 d_L과는 달리 분기 현상에 따른 Fractal 나무의 공간 채움(space filling) 정도를 정량화함을 알 수 있다.

만약 자연유역의 하천망을 Fig. 2와 동일한 분기 특성을 갖는 Fractal 도형으로 간주할 경우 Eqs. (1) and (2)는 Eqs. (10) and (11)과 개념적으로 일치하게 된다. 즉 Fractal 나무의 성장 단계별 가지의 개수 n과 길이의 변화율 $λ$ 는 각각 하천망의 분기비 R_B와 길이비 R_L에 해당하게 되는 것이다. 따라서 Eq. (14)의 d_N은 Eq. (9)와 유사하게 Horton 비의 함수형태로 변환할 수 있게 된다.

(15)

d_{N} = \frac{\ln R_{B}}{\ln R_{L}}

여기서 $λ$ 와 R_L은 각각 Fractal 나뭇가지의 축소율 및 차수별 하천길이의 성장률을 의미하는 것으로 양자는 서로 반대의 부호를 취하게 됨을 알 수 있다. Eq. (15)는 La Barbera and Rosso (1989)가 제시한 하천망의 Fractal 차원에 대한 관계식과 일치하는 결과로서 선의 형태로 이루어진 하천들이 면의 형태로 이루어진 유역을 완전히 배수하기 위하여 망상 구조를 조직해 가는 규모별 거동특성으로 해석할 수 있다.

3. 방법론

3.1 대상 유역

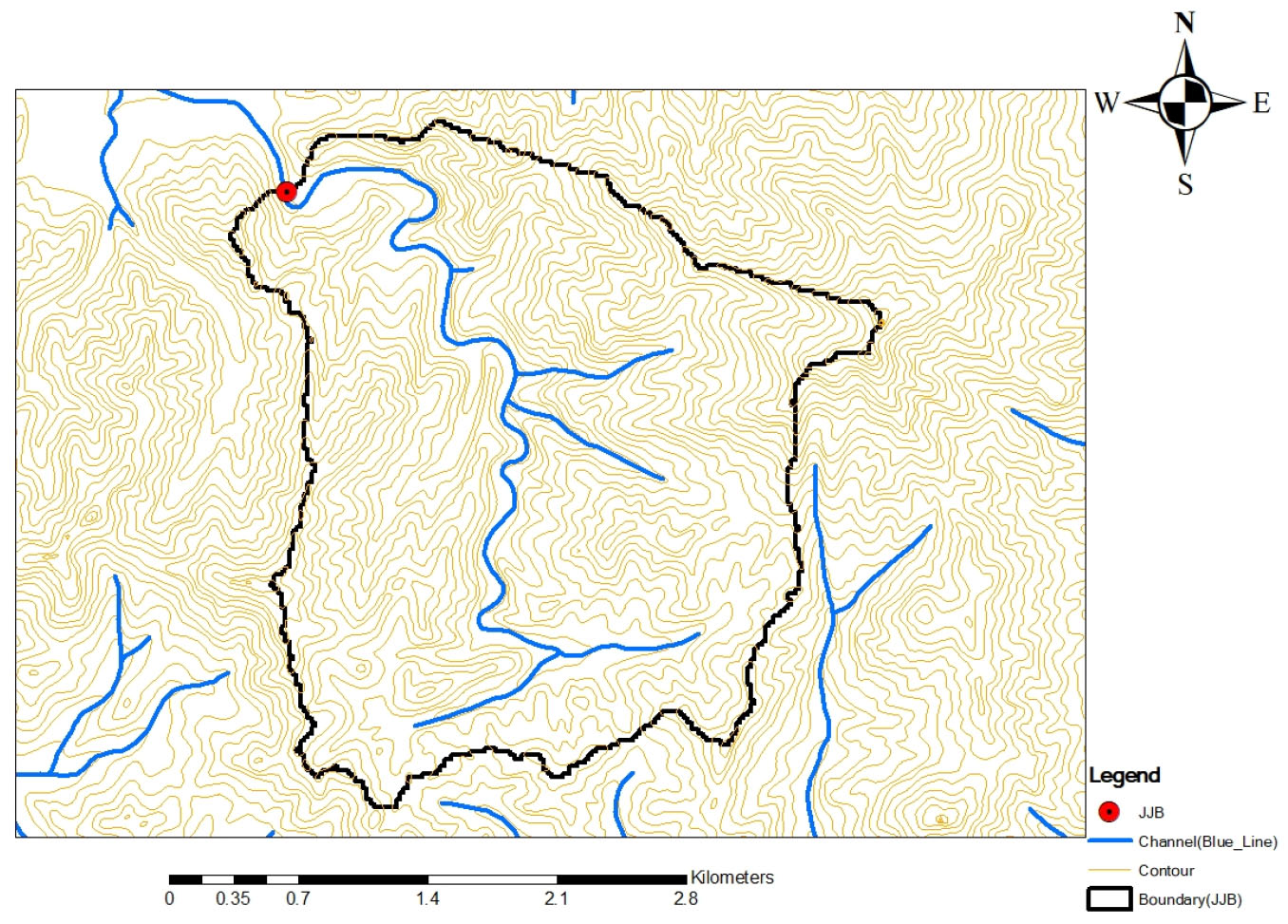
본 연구에서는 대상 유역으로 임진강 수계의 설마천 시험유역을 선정하였다. 설마천 시험유역은 영국군 전적비교(JJB) 지점을 출구로 하는 유역면적이 약 8.5 km²인 소규모 산악유역이다. Fig. 3은 대상 유역에 대한 배수 유역도를 도시한 것으로 좌측 상단의 기호 ◉는 JJB 지점의 위치를 나타낸다. Fig. 3에 도시한 하천망(Blue Line)은 국립지리원에서 발행한 1:25,000 축척의 수치 지도에 수록되어 있는 현장측량 결과로서 Strahler의 차수 기법에 따라 최고 차수 $Ω$ 는 2임을 쉽게 알 수 있다.

3.2 지형분석

현재 지리정보처리기술은 특정 해상도 상에서 정의되는 유역 내부의 모든 배수 경로를 도시화할 수 있는 수준에 도달하고 있다. 이에 따라 본 연구에서는 전술한 Fractal 나무의 성장 과정을 기반으로 유역 내부에서 발생할 수 있는 모든 배수 경로를 추출하여 하천 유동과 지표면 유동을 포괄할 수 있는 완전한 배수망을 구성하고 이에 해당하는 망상 구조가 가지는 Fractal 특성을 분석해 보고자 하였다(Kim and Kim, 2008; Kim and Jung, 2015). DEM의 생성에는 국립지리원에서 발행한 1:25,000 축척의 수치 지도를 적용하였는데 등고선과 표고점 layer를 포함한 수치지도를 기반으로 불규칙 삼각망(Triangulated Irregular Network, TIN)을 형성하여 등고선 사이에 표고를 내삽한 후 그 위에 격자(grid)를 중첩하였다. 여기서 pixel의 해상도는 20 × 20 m로 하였다. 지형분석 도구로는 Arc GIS 상에서 운용되는 TauDEM (Tarboton, 2003)을 적용하였으며 각 pixel별 흐름 방향은 8방향 모형을 이용하여 모의하였다. 또한, 기존의 설마천 시험유역에 대한 선행 연구들(Kim and Kim, 2008; Lee and Kim, 2011)과는 달리 본 연구에서는 Fig. 3에 도시한 수로망(현장측량 결과)과 보다 유사한 형태의 망상 구조를 추출하기 위하여 DEM의 전처리에 Stream Burning (Saunders and Maidment, 1996) 방법을 적용하였다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F3.jpg

Fig. 3

Seolma creek experimental basin

3.3 Fractal 차원의 산정

본 연구에서는 $L_{ω}$ 에 대하여 Eq. (7)과 유사한 형태의 scaling 법칙을 다음과 같이 가정하여 보았다.

(16)

L_{ω} \propto L_{ω ∥}^{d_{L}}

Eq. (16) 우변의 $L_{ω ∥}$ 는 $ω$ 차 하천의 시점과 종점 사이의 평균 직선거리(straight line length)를 의미하는 것으로 Eq. (7)의 $L_{∥}$ 과 개념적으로 동일한 역할을 한다. 여기서 만약 Eq. (14)의 r_k를 Eq. (16)을 이용하여 $L_{ω}$ 와 $L_{ω ∥}$ 로 치환할 경우 망상 구조의 Fractal 차원에 대한 관계식을 다음과 같이 유도할 수 있게 된다.

(17)

N (L_{ω}) \propto L_{ω}^{- d_{N}}

(18)

N (L_{ω ∥}) \propto L_{ω ∥}^{- D}; D = d_{N} d_{L}

Fractal 나무의 틀 내에서 동일한 차수에 대하여 Eqs. (17) and (18)의 $N (L_{ω})$ 와 $N (L_{ω ∥})$ 는 같은 값을 가짐을 알 수 있다. 이에 따라 Eq. (18) 우변의 D는 Tarboton et al. (1988)이 제시한 자연유역의 하천망에 대한 Fractal 차원에 해당하게 되며 d_N과 d_L의 곱으로 구성됨을 확인할 수 있게 된다.

한편 Eq. (16)의 관계를 Eq. (2)에 대입할 경우 R_L을 다음과 같이 $L_{ω ∥}$ 의 함수형태로 나타낼 수 있다.

(19)

R_{L} = \frac{L_{ω ∥}^{d_{L}}}{L_{ω - 1 ∥}^{d_{L}}} = {(\frac{L_{ω ∥}}{L_{ω - 1 ∥}})}^{d_{L}}

여기서 만약 $L_{ω ∥}$ 에 대하여 Eq. (2)와 유사하게 길이비( $R_{L ∥} = L_{ω ∥} / L_{ω - 1 ∥}$ )를 가정할 경우 해당 관계를 다음과 같이 변환할 수 있게 된다.

(20)

R_{L} = R_{L ∥}^{d_{L}}; d_{L} = \frac{\ln R_{L}}{\ln R_{L ∥}}

또한, Eq. (20)의 관계를 Eqs. (9), (15), (18)에 대입하여 정리할 경우 Eqs. (1) and (3) 역시 Eq. (20)과 유사한 형태로 나타낼 수 있게 된다.

(21)

R_{A} = R_{L ∥}^{1 + H}; 1 + H = \frac{\ln R_{A}}{\ln R_{L ∥}}

(22)

R_{B} = R_{L ∥}^{D}; D = \frac{\ln R_{B}}{\ln R_{L ∥}}

상기한 관계들은 Eq. (16)에 대한 가정을 기반으로 한 것으로 Yang and Paik (2017)이 제시한 관계식과 개념적으로 일치하는 것임을 확인할 수 있다. 본 연구에서는 사례분석을 통하여 해당 관계들의 타당성에 대한 검증과 함께 이들을 이용하여 자연유역의 Fractal 구조에 대한 해석을 수행하여 보았다.

4. 적용사례

4.1 Fractal 나무의 구성

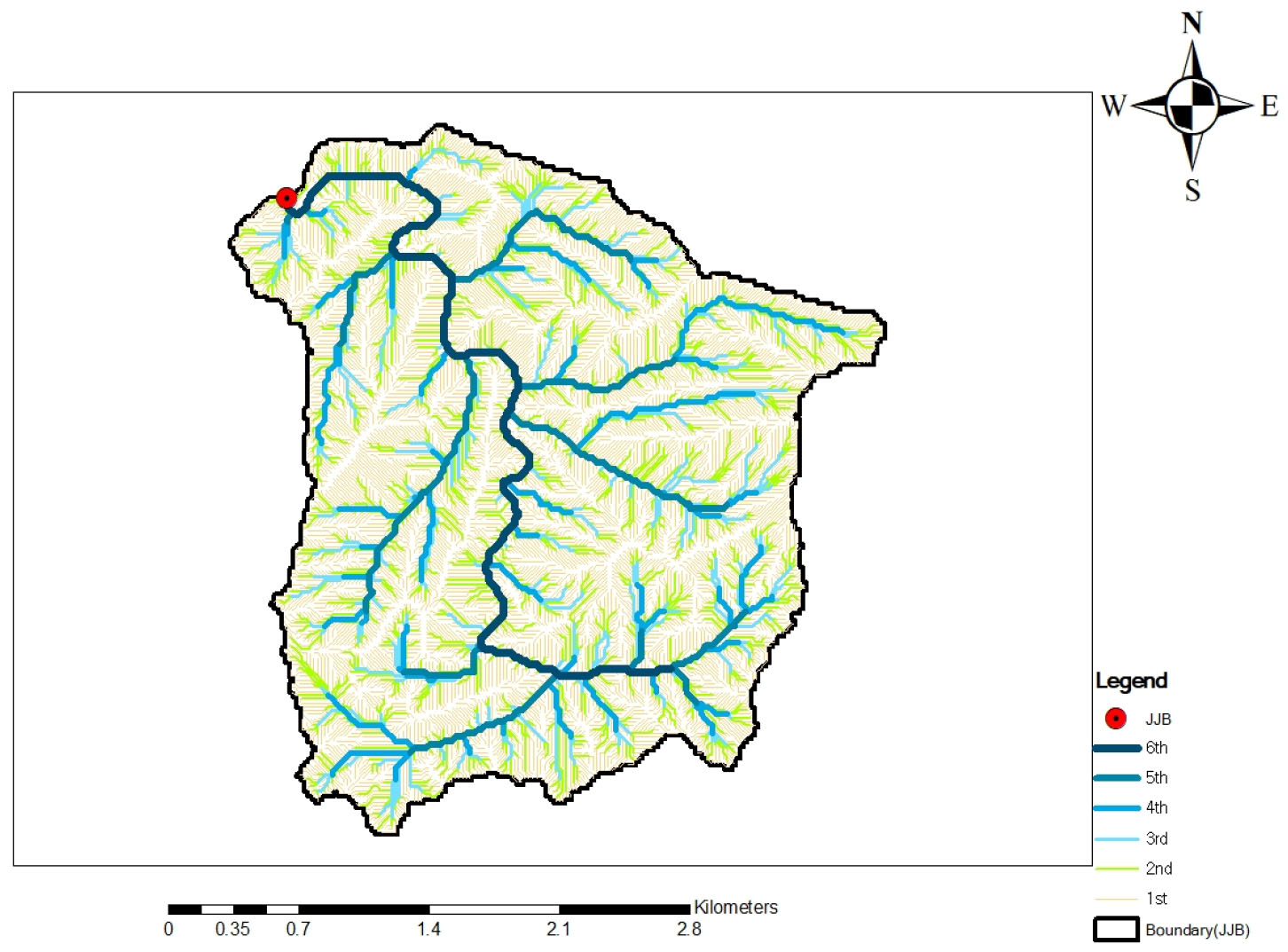
Fig. 4는 설마천 시험유역을 대상으로 본 연구에서 구성한 Fractal 나무를 도시한 것이다. 여기서 범례에 표시된 차수는 성장이 완료된 Fractal 나무에 Strahler의 차수 기법을 적용하여 위상 구조를 수립해 본 결과로서 대상 유역의 경우 Fractal 나무 몸통의 차수는 6차이며 총 5단계의 성장 과정을 거쳐 대상 유역 내부 공간을 완전히 채우게 됨을 볼 수 있다.

Table 1은 Fig. 4에 도시한 Fractal 나무의 특성을 Strahler의 차수 기법에 따라 정리한 것으로 Fractal 나무의 성장 단계(k)와 하천의 차수( $ω$ )가 서로 역순으로 증가함을 볼 수 있다. 여기서 마지막 열의 A₀는 Fractal 나무의 성장 단계별 유역 면적으로서 k의 증가에 따라 지속적으로 감소함을 확인할 수 있다. 주목되는 사항은 4단계와 5단계 성장 과정을 거쳐 분기한 Fractal 나뭇가지의 두 가지 길이 성분( $L_{ω ∥}$ 와 $L_{ω}$ )이 양자 모두 거의 유사한 값을 갖는 점이다. 이것은 마지막 단계(5단계)에서 분기한 나뭇가지들이 선행 단계에서 생성된 나뭇가지들과 상이한 성장 특성을 가짐을 의미하는 것으로 해당 단계에서 분기한 배수 경로들은 모두 지표면 유동 경로에 해당함을 쉽게 예상할 수 있다. 이러한 성장 단계의 이질성은 $A_{ω}$ 에 대한 산정 결과에서도 찾아볼 수 있는데 4단계와 5단계 성장 과정에 해당하는 $A_{ω}$ 는 $L_{ω ∥}$ 나 $L_{ω}$ 와는 다른 경향의 성장 특성을 가짐을 확인할 수 있다. 이로부터 자연유역 내부에서 Fractal 나무의 성장 과정은 하천 유동의 특성을 가지는 배수 경로에서만 제한적으로 나타날 수 있는 것으로 판단된다.

Table 1.

Topologic structure of seolma creek experimental basin

k	$ω$	$N_{ω}$	$L_{ω ∥}$ (m)	$L_{ω}$ (m)	$A_{ω}$ (m²)	$A_{0}$ (m²)
5	1	5011	69	72	1189	400
4	2	1168	72	75	4777	2659
3	3	245	105	112	17688	9693
2	4	54	225	247	82570	39378
1	5	11	675	779	544000	168836
0	6	1	3222	5610	8444800	618800

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F4.jpg

Fig. 4

Fractal tree of seolma creek experimental basin

4.2 망상 구조의 Fractal 차원

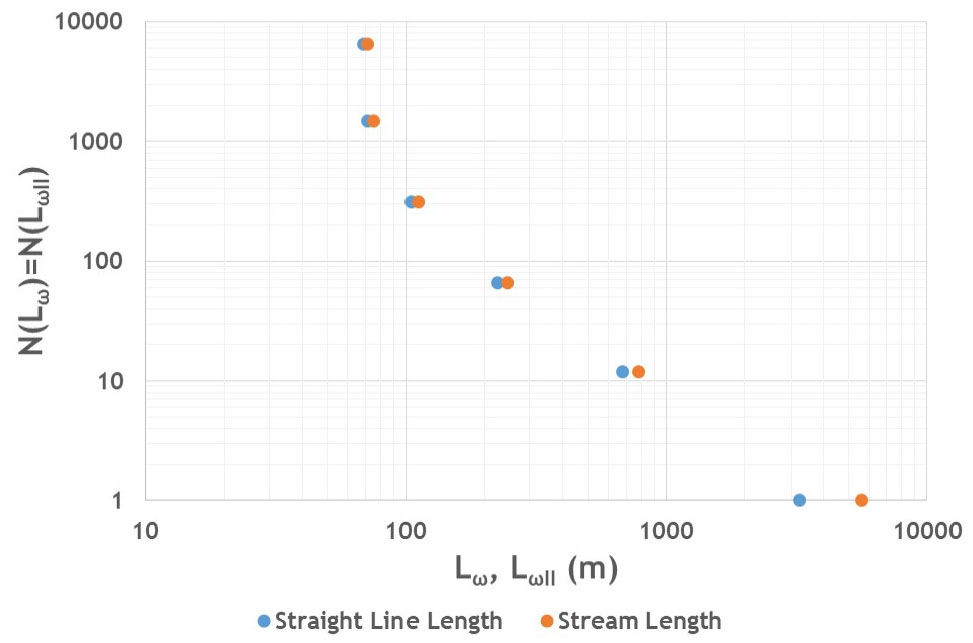
Fig. 5는 Table 1에 수록된 $N_{ω}$ , $L_{ω ∥}$ (straight line length)와 $L_{ω}$ (stream length)를 이용하여 Eqs. (17) and (18)의 관계를 중첩하여 도시한 것으로 원점 부근과 꼬리 부분에서 서로 상이한 거동특성이 나타남을 볼 수 있다. 우선, 꼬리 부분의 점들은 Eqs. (17) and (18)에 따라 양대수지 상에서 직선 형태로 나타나는 전형적인 규모 불변성(scale invariance)을 보여준다. 하지만 4단계와 5단계 성장 과정에 해당하는 원점 부근의 두 점은 전술한 바와 같이 $L_{ω ∥}$ 와 $L_{ω}$ 가 양자 모두 거의 유사한 길이를 가져 꼬리 부분에서 나타나는 Fractal 나무의 성장 과정과는 상이한 특성을 보임을 다시 한 번 확인할 수 있다.

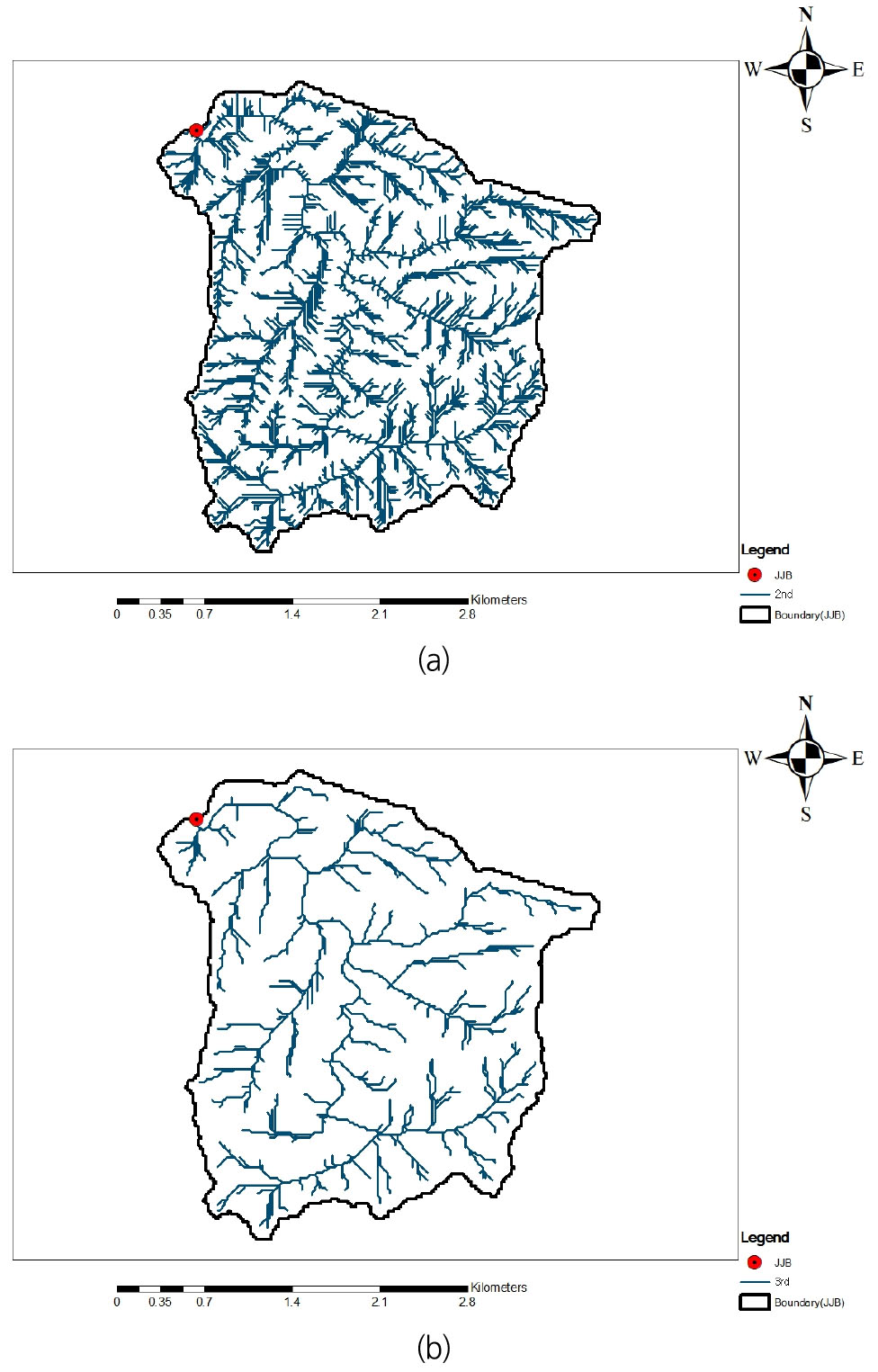
Kim and Kim (2008)과 Kim and Jung (2015)은 선행 연구를 통하여 Fig. 5와 유사한 그림을 도시한 후 단순히 시각적 판단(visual inspection)에 기초하여 3단계 성장 과정에 해당하는 원점 부근 세 번째 점을 전술한 두 가지 상이한 거동특성의 경계로서 제시한 바 있다. 하지만 4단계와 5단계 성장 과정 사이에 존재하는 이질적 거동특성이 3단계와 4단계 성장 과정 사이에도 존재하는지 여부는 Fig. 5만을 가지고 판단하기 어려울 것으로 보인다. 이에 따라 본 연구에서는 3단계와 4단계 성장 과정을 통하여 생성된 두 그루의 Fractal 나무를 Fig. 6과 같이 개별적으로 추출하여 각 망상 구조가 가지는 특성을 분석하여 보았다. 여기서 3단계와 4단계 성장 과정을 통해 생성된 Fractal 나무들은 $Ω$ 가 각각 4차(Fig. 6(b)) 및 5차(Fig. 6(a))에 해당하는 하천망임을 Fig. 6으로부터 확인할 수 있다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F5.jpg

Fig. 5

N ( $L_{ω}$ ) and N ( $L_{ω ∥}$ ) of seolma creek experimental basin

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F6.jpg

Fig. 6

Possible stream network of seolma creek experimental basin: (a) 5^th order, (b) 4^th order

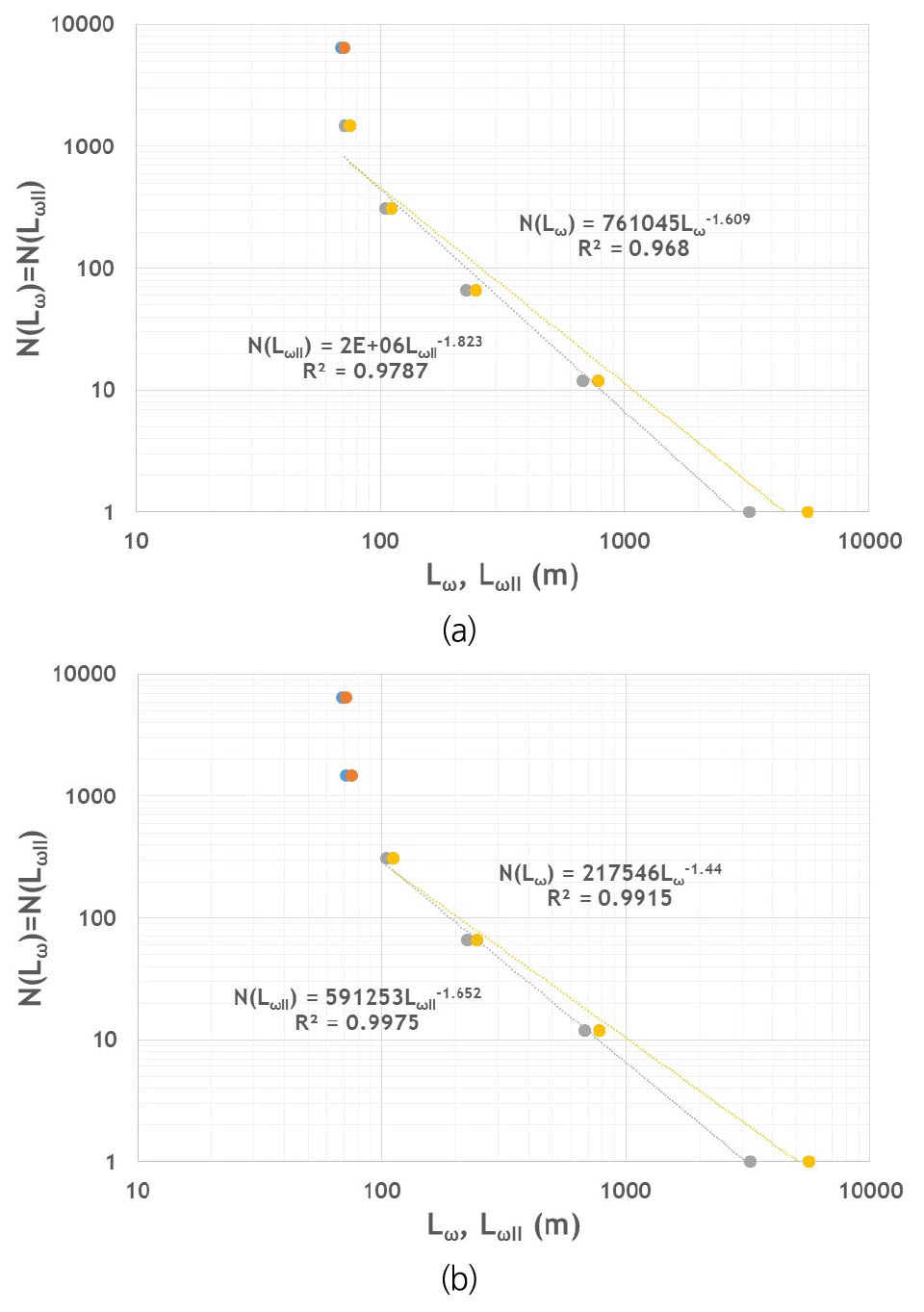
Fig. 7과 Table 2는 Fig. 6에 도시한 두 망상 구조에 대하여 Fractal 차원을 산정해 본 결과로서 Table 2에 수록된 d_L은 Fig. 7에 도시한 $L_{ω}$ 와 $L_{ω ∥}$ 에 대한 두 쌍의 회귀곡선들에 대한 기울기를 이용하여 간접적으로 산정한 결과이다. 여기서 주목되는 사항은 두 망상 구조에 대한 d_L과 d_N 사이의 변동성이 가지는 차이로 한 자릿수(one degree of magnitude)의 규모만큼 d_N이 더 크게 나타남을 볼 수 있다. 이는 Fractal 나무의 성장 단계(혹은 망상 구조의 해상도)에 따라 d_N이 d_L에 비하여 보다 민감하게 변화함을 의미하는 것으로서 Fig. 6의 두 망상 구조는 서로 중첩되어 있음에도 불구하고 Fractal 나무의 성장 과정을 통하여 서로 상이한 분기 특성을 가지게 됨이 예상된다. 이는 주로 중규모 이상의 유역(A ≥ 20 km²)을 대상으로 한 선행 연구들(Maritan et al., 1996; Rigon et al., 1996; Dodds and Rothman, 2000)에서 제시하는 규모 불변성의 원리와는 다소 상이한 결과임을 알 수 있다. 설마천 시험유역은 전술한 바와 같이 유역 면적이 약 8.5 km²의 소유역으로서 상시(常時) 하천망(perennial stream network)의 범위(Fig. 3)는 Fig. 6과는 상당한 차이를 보임을 쉽게 확인할 수 있다. 이에 따라 Fig. 6은 지표면에 내재하는 하천 유동의 특성을 Fractal 나무의 성장 과정에 따라 추출한 결과로 볼 수 있으며, 이를 Fig. 3과 비교할 경우 건기(乾期)에는 하천을 형성하지 못하지만 우기(雨期)가 되면 하천과 유사한 기능을 수행할 수 있는 다수의 임시(臨時) 하천(ephemeral stream) 형태의 배수 경로가 상시 하천망을 중심으로 발달 되어 있음으로 볼 수 있다. 건기와 우기가 지속적으로 반복되면서 하천망의 범위 역시 주기적으로 신장과 축소를 반복하게 되어(Godsey and Kirchner, 2014; Hooshyar et al., 2015) 상기한 임시 하천 형태의 배수 경로는 지표면과 상시 하천망 사이에 하천 유동의 특성을 갖는 일종의 천이 영역을 형성할 것이 예상된다. 결국 본 연구의 대상 유역인 설마천 시험유역의 경우 Fractal 나무의 성장 과정이 상시 하천망(1단계 성장)의 범위를 넘어서도 나타나게 되는 것으로 판단된다. 만약, 일정 수준 이상으로 발달된 상시 하천망이 존재하지 않는 소유역을 고려할 경우 전술한 임시 하천 형태의 배수 경로가 해당 유역의 유출 현상에 가지는 기여도는 무시할 수 없을 것이므로 소유역의 배수 구조는 Fig. 3보다는 Fig. 6과 같은 망상 구조가 대표할 수 있을 것으로 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F7.jpg

Fig. 7

D and d_N of seolma creek experimental basin: (a) 5^th order, (b) 4^th order

Table 2.

Fractal dimension of seolma creek experimental basin

$Ω$	d_N	D	d_L (= D/d_N)
4th	1.440	1.652	1.147
5th	1.609	1.823	1.133

한편 두 망상 구조에 대한 Fractal 차원의 추정 결과는 선행 연구(Tarboton et al., 1988; La Barbera and Rosso (1989); Rosso et al., 1991)에서 제시하고 있는 자연 유역의 하천망에 대한 범위에 근사적으로 포함되지만, 국내 유역을 대상으로 하여 Yang and Paik (2017)이 제시한 결과와 비교할 경우 다소 상이한 경향을 보임을 확인할 수 있다. 전술한 바와 같이 Fig. 6에 도시한 두 하천망은 상시 하천망과 임시 하천 형태의 배수 경로를 모두 포함하고 있는 것으로서 강우 유입량의 조건에 따라 변동될 가능성이 있을 것으로 판단된다. 따라서 Fig. 6은 우기에 설마천 시험유역 내에 출현할 수 있는 배수망의 최대 범위로 해석할 수 있을 것이다. Yang and Paik (2017)이 제시한 결과의 경우 상시 하천망을 대상으로 한 결과로서 결국 이러한 차이는 고려하는 하천망의 범위가 상이하기 때문에 나타나는 것으로 판단된다. 이에 따라 본 연구의 대상 유역인 설마천 시험유역의 Fractal 차원은 d_L은 1.133 ~ 1.147 그리고 D는 1.652 ~ 1.823의 범위를 갖는 것으로 판단되어 진다.

4.3 Hack의 법칙

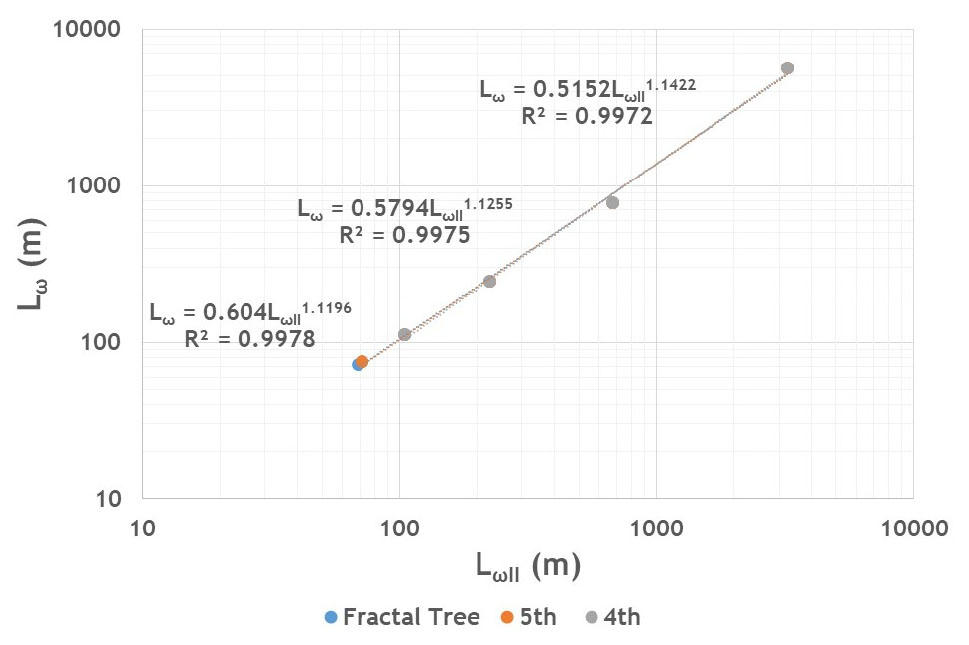
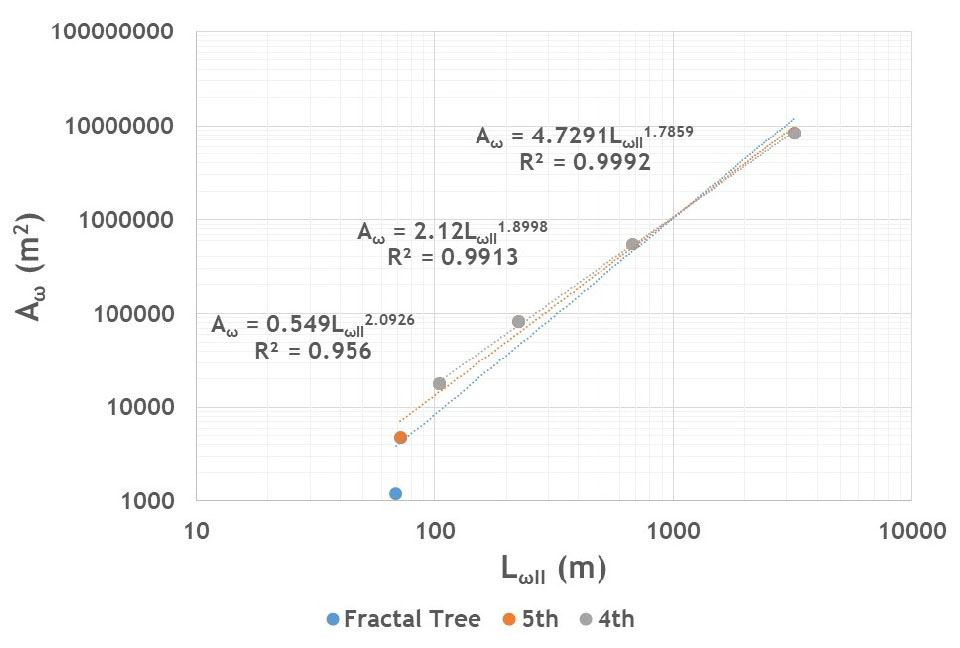
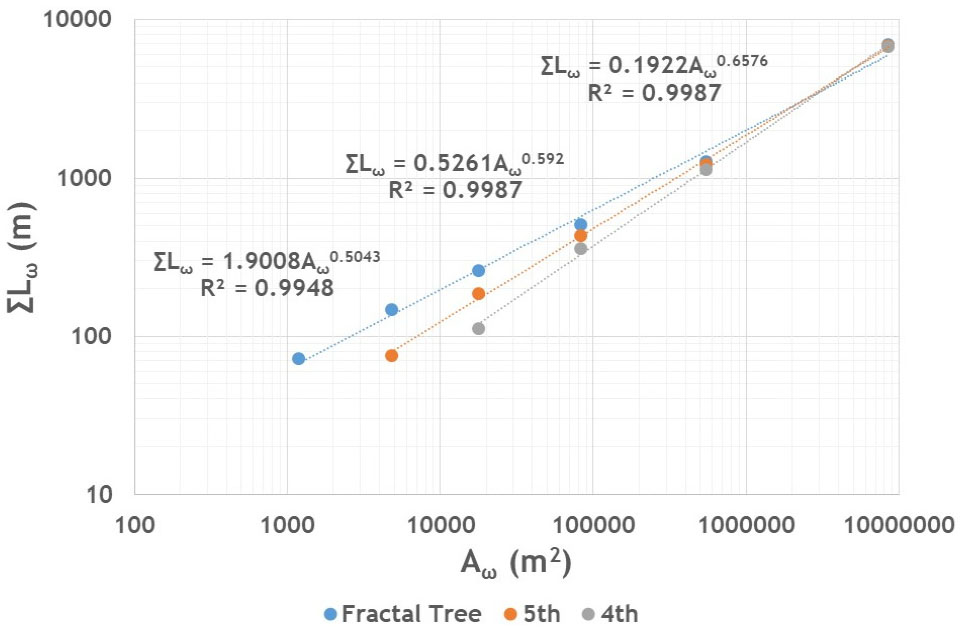
Figs. 8 and 9는 Eqs. (6) and (7)의 관계를 Eq. (16)의 가정에 따라 도시한 것으로 Fig. 6의 4차 및 5차 하천망과 함께 Fig. 4의 Fractal 나무(6차 하천망) 등 총 세 개의 망상 구조를 대상으로 작성하여 보았다. Table 3의 2열과 3열은 이들을 정리한 것으로 d_L의 경우 4차와 5차 하천망에 대하여 Table 2의 결과와 상당히 유사하게 나타남을 확인할 수 있다. 이는 Table 2에 수록된 d_L값이 Eqs. (17) and (18)을 기반으로 간접적으로 추정했음에도 불구하고 신뢰성이 있음을 나타내는 결과로서 이에 따라 본 연구에서 제시한 Fractal 차원에 대한 관계식의 타당성을 입증하는 결과로 판단된다. 여기서 한 가지 주목되는 사항은 Fractal 나무의 성장 과정이 진행됨에 따라 d_L 값이 다소 감소하는 경향을 보이는 것으로 이는 성장 단계가 커질수록 판상류(sheet flow) 형태의 지표면 유동의 영향이 커짐에 기인하는 것으로 보여진다. 하지만 차수 간 변동성의 규모는 전술한 바와 같이 d_N에 비하여 작게 나타남을 볼 수 있어 설마천 시험유역의 경우 단일 하천 구간에 대한 Fractal 차원 d_L은 유역 전반에 걸쳐 일정하게 제시하는 것(예를 들어 $d_{L} = 1.129$ )도 타당한 것으로 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F8.jpg

Fig. 8

d_L of seolma creek experimental basin

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F9.jpg

Fig. 9

1+H of seolma creek experimental basin

Table 3.

Scaling property of seolma creek experimental basin

$Ω$	d_L	H	h_cal	h_obs
4th	1.142	0.786	0.640	0.658
5th	1.126	0.900	0.592	0.592
Fractal Tree (6th)	1.120	1.093	0.535	0.504

Table 3의 H는 d_L에 비하여 한 자릿수의 규모만큼 크게 변동이 나타남을 볼 수 있다. 이는 Fractal 나무의 성장 과정에 따라 집수평면의 형상이 가지는 이방성 성장 특성이 변동되어감을 나타내는 것으로 설마천 시험유역의 경우 하류 방향으로 규모가 커짐에 따라 집수평면의 형상이 점점 더 빠르게 신장(伸張)되어 감을 의미한다. Fig. 10은 Hack의 법칙을 세 개의 망상 구조에 적용한 것으로 차수( $ω$ )가 증가함에 따라 주하천 연장을 $L = \sum_{i = 1}^{ω} L_{i}$ 로 평가하여 단일 유역에 대한 Eq. (8)의 관계(Maritan et al., 1996; Rigon et al., 1996; Dodds and Rothman, 2000)를 각 망상 구조에 대하여 도시한 것이다. Table 3의 3열과 4열은 h에 대한 추정결과를 정리한 것으로 h_cal는 Eq. (8)에 의해 산정된 값이고 h_obs는 Fig. 10에 도시한 회귀곡선들에 대한 기울기로서 각 차수별로 유사한 결과를 나타냄을 볼 수 있다. 이는 Table 3에 수록된 H에 대한 추정결과가 타당함을 의미하는 것이다. Dodds and Rothman (2000)은 Fig. 10과 같이 단일 유역에 대하여 Hack의 법칙을 도시할 경우 지표면과 상시 하천망 사이에서 h 값의 변동 구간이 존재함을 제시하였다. 이것은 Table 3 및 Fig. 10의 결과와 유사한 것으로 이에 따라 Table 2에서 제시한 d_N과 D의 변동성은 타당한 결과인 것으로 판단된다. 설마천 시험유역과 같이 소규모 유역의 경우 h 값의 변동이 나타나는 구간이 유역 내부에 상당 부분 존재할 것이며 이는 d_N에 영향을 미쳐 단일한 수치의 고정된 형태로 D 값을 제시하는 것은 불가능할 수 있다. 따라서 전 절에서 제시한 D의 범위는 설마천 시험유역의 Fractal 구조를 대표하는 중요한 정보인 것으로 판단된다.

https://static.apub.kr/journalsite/sites/kwra/2021-054-01/N0200540105/images/kwra_54_01_05_F10.jpg

Fig. 10

Hack’s law of seolma creek experimental basin

4.4 Horton 비

Table 4는 전 절에서 고려한 세 개의 망상 구조에 대하여 Horton 비를 산정한 결과로서 본 연구에서는 Eqs. (1) ~ (3)의 관계에 $L_{ω ∥}$ 를 기반으로 한 길이비 $R_{L ∥}$ 를 추가하였다. 여기서 R_L은 선행 연구에서 제시한 범위(Smart, 1972)를 만족하지만 R_B와 R_A는 4차와 5차 하천망의 경우 선행 연구에서 제시한 범위보다 큰 값으로 나타남을 볼 수 있다. 전술한 바와 같이 두 하천망은 우기에 설마천 시험유역 내에 출현할 수 있는 배수망의 최대 범위로서 Leopold and Miller (1956)는 임시 하천 형태의 배수경로의 특성을 상시 하천망과 비교할 경우 그 규모는 작지만 개수가 훨씬 많음을 제시한 바 있다. 이에 따라 본 연구에서 추정한 R_B와 R_A는 상시 하천망을 대상으로 제시된 선행 연구의 범위를 벗어나 큰 값을 보이는 것으로 판단된다.

Table 4.

Horton ratios of seolma creek experimental basin

$Ω$	R_B	R_L	$R_{L ∥}$	R_A
4th	6.107	3.361	3.119	7.684
5th	5.601	2.875	2.578	6.285
6th	5.260	2.330	2.145	5.566

Table 5는 Table 4에 수록된 Horton 비를 Eqs. (20) ~ (22)에 적용하여 d_L, H, D를 산정한 결과로서 Table 2와 Table 3에 수록된 결과와 유사한 값을 가지며 비슷한 경향을 보임을 확인할 수 있다. 여기서 5열의 d_N은 Eq. (15)를 이용하여 산정한 결과이다. 일반적으로 하천망의 Fractal 차원은 서론에서 언급한 Richardson의 방법이나 box counting 방법과 같은 도해적 방법에 따라 추정된다. Eq. (15)는 이러한 도해적 방법에 대한 일종의 대안으로 평가할 수 있는바 본 연구에서 Fractal 나무의 개념을 기반으로 제시한 Fractal 차원에 대한 추정방법은 타당한 접근임을 다시 한번 확인할 수 있다.

Table 5.

Fractal dimension of seolma creek experimental basin by Horton ratios

$Ω$	d_L	H	D	d_N
4th	1.134	0.792	1.591	1.403
5th	1.115	0.941	1.819	1.632
6th	1.108	1.249	2.175	1.963

Table 5에서 한 가지 주목되는 사항으로 6차 하천망의 경우 D가 2를 초과하여 나타남을 볼 수 있다. 전술한 바와 같이 Fractal 나무의 성장은 상시 하천망과 그 주변에 위치한 천이 영역에서만 나타나는 것으로서 결국 Fig. 4에 도시한 배수망의 말단에 위치한 가지들은 Fractal 나무의 성장을 따르지 않는 것으로 판단할 수 있다. 결국 이러한 분기 구조의 이질성에 따라 D가 2를 초과하여 나타나는 것으로 보인다. 6차 하천망의 H에 대한 산정 결과에서도 유사한 특성을 확인할 수 있다.

5. 결 론

본 연구의 주목적은 자연유역의 배수 구조에 내재한 두 가지 개별적 Fractal 차원을 Fractal 나무의 틀 내에서 동시에 평가할 수 있는 방법론을 제시해보고자 하는 것이다. 이를 위하여 Fractal 나무의 성장 과정을 기반으로 유역 내부에서 발생할 수 있는 모든 배수 경로를 추출하여 하천 유동과 지표면 유동을 포괄할 수 있는 완전한 배수망을 구성하고 이에 해당하는 망상 구조가 가지는 Fractal 특성을 분석해 보고자 하였다. 특히 소유역에 대한 사례분석을 통하여 중소규모의 유역을 대상으로 한 수문학적 실무에 있어 Fractal 차원에 대한 개념을 유용하게 이용할 수 있는 기초를 제공하고자 하였다. 이상으로부터 얻어진 주요한 결론을 요약해 보면 다음과 같다.

1) 자연유역 내부에서 Fractal 나무의 성장 과정은 하천 유동의 특성을 가지는 배수 경로에서만 제한적으로 나타날 수 있다.

2) 소규모 유역의 경우 Fractal 나무의 성장 단계에 따라 망상 구조의 분기 특성이 단일 하천 구간의 사행 특성에 비하여 민감하게 변화한다. 이에 따라 단일한 망상 구조 속에서도 Fractal 나무의 성장 과정을 통하여 서로 상이한 분기 특성이 나타날 수 있다.

3) 따라서 소규모 유역의 단일 하천 구간에 대한 Fractal 차원은 유역 전반에 걸쳐 일정하게 평가할 수 있지만 망상 구조로서의 하천망에 대한 Fractal 차원은 집수평면의 이방성 성장 특성을 고려하여 단일한 수치의 고정된 형태보다는 범위의 형태로 취급되어야 하는 것이 타당한 것으로 판단된다.

4) 소규모 유역의 경우 건기에는 하천을 형성하지 못하지만 우기가 되면 하천과 유사한 기능을 수행할 수 있는 다수의 임시 하천 형태의 배수 경로가 상시 하천망을 중심으로 발달 되어 해당 유역의 유출 현상에 기여하는 것으로 판단된다.

5) 이에 따라 소규모 유역의 배수 구조에 대한 분석에는 지형도나 수치 지도로부터 추출한 하천망보다 본 연구에서 제시한 Fractal 나무의 성장에 따른 망상 구조와 같은 정보가 더 유용할 것으로 판단된다.

Acknowledgements

본 연구는 충남대학교와 환경부의 재원으로 한국환경산업기술원의 물관리연구사업의 지원을 받아 수행되었습니다(79610).

References

Agnese, C., D'Asaro, F., Grosso, G., and Rosso, R. (1996). "Scaling properties of topologically random channel network." Journal of Hydrology, Vol. 187, pp. 183-193. 10.1016/S0022-1694(96)03095-8

Beer, T., and Borgas, M. (1993). "Horton's law and the Fractal nature of streams." Water Resources Research, Vol. 29, No. 5, pp. 1475-1487. 10.1029/92WR02731

Dodds, P.S., and Rothman, D.H. (2000). "Scaling, universality, and geomorphology." Annual Review of Earth and Planetary Sciences, Vol. 28, pp. 571-610. 10.1146/annurev.earth.28.1.571

Godsey, S.E., and Kirchner, J.W. (2014). "Dynamic, discontinuous stream networks: hydrologically driven variations in active drainage density, flowing channels and stream order." Hydrological Process, Vol. 28, pp. 5791-5803. 10.1002/hyp.10310

Hack, J.T. (1957). Studies of longitudinal profiles in Virginia and Maryland. US Geological Survey Professional Paper, 294-B, United States Geological Survey, Reston, V.A., U.S., pp. 45-97. 10.3133/pp294B

Hergarten, S. (2002). Self-organized criticality in earth system, Springer-Verlag, N.Y., U.S. 10.1007/978-3-662-04390-5

Hooshyar, M., Kim, S., Wang, D., and Medeiros, S.C. (2015). "Wet channel network extraction by integrating LiDAR intensity and elevation data." Water Resources Research, Vol. 51, pp. 10029-10046. 10.1002/2015WR018021

Horton, R.E. (1945). "Erosional development of streams and their drainage basin: hydrophysical approach to quantitative morphology." Bulletin of the Geological Society of America, Vol. 13, No. 3, pp. 275-370. 10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2

Ijjasz-Vasquez, E.J., and Bras, R.L. (1995). "Scaling regimes of local slope versus contributing area in digital elevation models." Geomorphology, Vol. 12, pp. 299-311. 10.1016/0169-555X(95)00012-T

Kim, J.C., and Jung, K. (2015). "Fractal tree analysis of drainage patterns." Water Resources Management, Vol. 29, pp. 1217-1230. 10.1007/s11269-014-0869-7

Kim, J.C., and Kim, J.H. (2007). "Morphological representation of channel network by dint of DEM." Journal of Korea Water Resources Association, Vol. 40, No. 6, pp. 287-297. 10.3741/JKWRA.2007.40.4.287

Kim, J.C., and Kim, J.H. (2008). "The geometric properties of the drainage structures based on fractal tree." Journal of Korea Water Resources Association, Vol. 41, No. 8, pp. 797-806. 10.3741/JKWRA.2008.41.8.797

Kim, J.C., and Lee, S.J. (2009). "Hack's law and the geometric properties of catchment plan-form." Journal of Korea Water Resources Association, Vol. 42, No. 9, pp. 691-702. 10.3741/JKWRA.2009.42.9.691

La Barbera, P., and Rosso, R. (1989). "On the fractal dimension of stream networks." Water Resources Research, Vol. 25, No. 4, pp. 735-741. 10.1029/WR025i004p00735

Lee, G., and Kim, J.C. (2011). "Comparative analysis of geomorphologic characteristics of DEM-based drainage networks." Journal of Hydrologic Engineering, Vol. 16, No. 2, pp. 137-147. 10.1061/(ASCE)HE.1943-5584.0000295

Leopold, L.B., and Miller, J.P. (1956). Ephemeral streams-hydraulic factors and their relation to the drainage net. US Geological Survey Professional Paper, 282-A, United States Geological Survey, Reston, V.A., U.S., pp. 1-42. 10.3133/pp282A

Mandelbrot, B.B. (1982). The Fractal geometry of nature, W. H. Freeman, N.Y., U.S.

Maritan, A., Rinaldo, A., Rigon, A., Giacometti, A., and Rodriguez-Iturbe, I. (1996). "Scaling laws for river networks." Physical Review E, Vol. 53, No. 2, pp. 1510-1515. 10.1103/PhysRevE.53.15109964414

Montgomery, D.R., and Foufoula-Georgiou, E. (1993). "Channel network source representation using digital elevation models." Water Resources Research, Vol. 29, No. 12, pp. 3925-3934. 10.1029/93WR02463

Moussa, R. (2003). "On morphometric properties of basins, scale effects and hydrological response." Hydrological Processes, Vol. 17, pp. 33-58. 10.1002/hyp.1114

Moussa, R., and Bocquillon, C. (1996). "Fractal analyses of tree-like networks from digital elevation model data." Journal of Hydrology, Vol. 187, pp. 157-172. 10.1016/S0022-1694(96)03093-4

Newman, W.I., Turcotte, D.L., and Gabrielov, A.M. (1997). "Fractal trees with side branching." Fractals, Vol. 5, No. 4, pp. 603-614. 10.1142/S0218348X97000486

O'Callaghan, J.F., and Mark, D.M. (1984). "The extraction of drainage networks from digital elevation data." Computer Vision, Graphics, and Image Processing, Vol. 28, pp. 324-344. 10.1016/S0734-189X(84)80011-0

Peckham, S.D. (1995). "New results for self-similar trees with applications to river networks." Water Resources Research, Vol. 31, No. 4, pp. 1023-1029. 10.1029/94WR03155

Puente, C.E., and Castillo, P.A. (1996). "On the fractal structure of networks and dividers within a watershed." Journal of Hydrology, Vol. 187, pp. 173-181. 10.1016/S0022-1694(96)03094-6

Rigon, R., Rodriguez-Iturbe, I., Maritan, A., Giacometti, A., Tarboton, D.G., and Rinaldo, A. (1996). "On Hack's law." Water Resources Research, Vol. 32, No. 11, pp. 3367-3374. 10.1029/96WR02397

Rosso, R., Bacchi, B., and La Barbera, P. (1991). "Fractal relation of mainstream length to catchment area in river networks." Water Resources Research, Vol. 27, No. 3, pp. 381-387. 10.1029/90WR02404

Saunders, W.K., and Maidment, D.R. (1996). A GIS assessment of nonpoint source pollution in the San Antonio-Nueces Coastal basin. Center for Research in Water Resources, University of Texas, Austin, T.X., U.S.

Schumm, S.A. (1956). "Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey." Geological society of America bulletin, Vol. 67, No. 5, pp. 597-646. 10.1130/0016-7606(1956)67[597:EODSAS]2.0.CO;2

Shreve, R.L. (1966). "Statistical law of stream numbers." Journal of Geology, Vol. 74, pp. 17-37. 10.1086/627137

Smart, J.S. (1972). "Channel networks." Advanced in Hydrosciense, Vol. 8, pp. 350-346. 10.1016/B978-0-12-021808-0.50011-5

Tarboton, D.G. (1996). "Fractal river networks, Horton's laws and Tokunaga cyclicity." Journal of Hydrology, Vol. 187, pp. 105-117. 10.1016/S0022-1694(96)03089-2

Tarboton, D.G. (2003). "Terrain analysis using digital elevation models in hydrology." 23rd ESRI International Users Conference, San Diego, C.A., U.S.

Tarboton, D.G., Bras, R.L., and Rodriguez-Iturbe, I. (1988). "The fractal nature of river networks." Water Resources Research, Vol. 24, No. 8, pp. 1317-1322. 10.1029/WR024i008p01317

Tarboton, D.G., Bras, R.L., and Rodriguez-Iturbe, I. (1992). "A physical basis for drainage density." Geomophology, Vol. 5, pp. 59-75. 10.1016/0169-555X(92)90058-V

Tokunaga, E. (1966). "The composition of drainage network in Toyohira River basin and Horton's first law." Geophysical Bulletin of Hokkaido University, Vol. 15, pp. 1-19.

Yang, S., and Paik, K. (2017). "New findings on river network organization: Law of eigenarea and relationships among Hortonian scaling ratios." Fractals, Vol. 25, No. 3, 1750029. 10.1142/S0218348X17500293

Journal of Korea Water Resources AssociationISSN:2799-8746(Print) 2799-8754(Online)한국수자원학회

Preview

Estimation of fractal dimension for Seolma creek experimental basin on the basis of fractal tree concept

ABSTRACT

MAIN

(1)

(2)

(3)

Fig. 1

Catchment planform

(4)

(5)

(6)

(7)

(8)

(9)

Fig. 2

Fractal tree

(10)

(11)

(12)

(13)

(14)

(15)

Fig. 3

Seolma creek experimental basin

(16)

(17)

(18)

(19)

(20)

(21)

(22)

Table 1.

Topologic structure of seolma creek experimental basin

Fig. 4

Fractal tree of seolma creek experimental basin

Fig. 5

N (Lω) and N (Lω∥) of seolma creek experimental basin

Fig. 6

Possible stream network of seolma creek experimental basin: (a) 5th order, (b) 4th order

Fig. 7

D and dN of seolma creek experimental basin: (a) 5th order, (b) 4th order

Table 2.

Fractal dimension of seolma creek experimental basin

Fig. 8

dL of seolma creek experimental basin

Fig. 9

1+H of seolma creek experimental basin

Table 3.

Scaling property of seolma creek experimental basin

Fig. 10

Hack’s law of seolma creek experimental basin

Table 4.

Horton ratios of seolma creek experimental basin

Table 5.

Fractal dimension of seolma creek experimental basin by Horton ratios

Acknowledgements

References

N ( $L_{ω}$ ) and N ( $L_{ω ∥}$ ) of seolma creek experimental basin

Possible stream network of seolma creek experimental basin: (a) 5^th order, (b) 4^th order

D and d_N of seolma creek experimental basin: (a) 5^th order, (b) 4^th order

d_L of seolma creek experimental basin