Identification of unit hydrograph peak behavior according to changes in precipitation scale in a virtual watershed

Ju-Hwan Yoo; Joo-Cheol Kim

doi:10.3741/JKWRA.2023.56.10.655

Preview

Research Article

Journal of Korea Water Resources Association. 31 October 2023. 655-665
https://doi.org/10.3741/JKWRA.2023.56.10.655

Identification of unit hydrograph peak behavior according to changes in precipitation scale in a virtual watershed

가상 유역의 강수 규모 변화에 따른 단위유량도 첨두치의 거동 규명

Ju-Hwan Yoo^a

Joo-Cheol Kim^b^*

유 주환^a

김 주철^b^*

^aProfessor, Department of Drone Application, U1 University, Asan, Korea

^bChief Researcher, International Water Resources Research Institute, Chungnam National University, Daejeon, Korea

^a유원대학교 드론응용학과 교수

^b충남대학교 국제수자원연구소 수석연구원

^{*Corresponding Author}

ABSTRACT

In this study, unit hydrographs are calculated when precipitations of 10 scales instantaneously occurs in a virtual watershed with a constant slope and roughness. Then, the relationship between the peak flow rate and the peak occurrence time of the unit hydrograph was calculated for the precipitation scale, respectively. At this time, the virtual watershed simplified with a rhombic shape, a constant slope, and a flow condition with a certain roughness was applied instead of a natural watershed in order to understand the effect the precipitation scale has on the peak value of the unit hydrograph. And it was assumed that the precipitation in the basin was effective rainfall and the runoff was direct runoff, and the runoff flowed in a straight, uniform flow from the drop point to the outlet. The relationship between the peak flow and the peak occurrence time of the unit hydrograph was calculated in the case of 10 types of precipitation scales of 10 mm, 40 mm, 90 mm, 160 mm, 250 mm, 360 mm, 640 mm, 1,000 mm, 1,210 mm, and 1,690 mm of effective precipitation. A noteworthy achievement of this study is that, even without the storage effect of the watershed, as the scale of precipitation increases, the depth of runoff increases, so the flow rate in the watershed increases and the distance per unit time increases, so the peak flow rate increases and the peak occurrence time increases. This is a nonlinear characteristic of watershed runoff.

Keywords

Unit hydrograph

Peak flow

Time to peak

Precipitation scale

Nonlinear runoff

본 연구에서는 일정한 경사와 조도를 갖는 가상 유역에서 10가지 규모의 강수가 순간적으로 발생할 때 단위유량도를 산출하였다. 그런 다음 강수 규모에 대하여 단위유량도 첨두유량의 관계와 첨두발생시간의 관계를 각각 산출하였다. 이때 강수 규모만이 유역의 단위유량도 첨두치에 주는 영향을 파악하기 위해서 자연 유역을 대신하여 마름모 형태, 일정 경사, 일정 조도의 유로 환경 상태 등으로 단순화한 가상 유역을 적용하였다. 그리고 유역에 내린 강수는 유효우량이고 유출은 직접유출이고 낙하지점에서 출구 방향으로 직선적인 등류로 유출된다고 가정하였다. 강수 규모를 10가지로 유효강수 10 mm, 40 mm, 90 mm, 160 mm, 250 mm, 360 mm, 640 mm, 1,000 mm, 1,210 mm, 1,690 mm의 경우로 하여 단위유량도의 첨두유량과 첨두발생시간을 각각의 관계를 산출하였다. 본 연구에서 주목할 만한 성과는 유역의 저류 효과가 없어도 강수 규모가 커질수록 유출 깊이가 커져서 유역의 유속이 빨라지고 단위 시간당 유하 거리도 커지므로 첨두유량은 커지고 첨두발생시간은 빨라진다는 것이었다. 이는 유역 유출의 비선형적 특성이다.

키워드

단위유량도

첨두유량

첨두발생시간

강수 규모

비선형 유출

MAIN

1. 서 론
1.1 연구 배경 및 목적
1.2 연구 범위 및 제한점
2. 연구 방법 및 과정
2.1 접근 방법
2.2 기본 설정
2.3 강수 규모 사례 설정
2.4 강수 규모별 사례 연구
3. 연구 결과 및 분석
3.1 강수 규모별 단위유량도
3.2 강수 규모별 단위유량도의 첨두유량과 첨두발생시간
3.3 강수 규모와 단위유량도 첨두유량의 관계 분석
3.4 강수 규모와 단위유량도 첨두발생시간의 관계 분석
3.5 단위유량도의 첨두유량에 따른 첨두발생시간 관계 분석
3.6 기존 연구와 본 연구성과 비교
4. 주요 연구 결과 및 결론

1. 서 론

1.1 연구 배경 및 목적

단위유량도 이론(Sherman, 1932)에 의하면 강수에 대한 유역의 응답이 선형성을 갖는다. 즉 이론에 따르면 어떤 한 유역의 단위유량도는 강수의 규모와 관계없이 단위유량도는 일정하고 선형성을 갖기 때문에 복합 강수에 대한 회선적분(convolution integral)을 통하여 비례와 중첩의 원리에 의하여 홍수 유출 수문곡선을 산출한다. 유역의 홍수량을 산출하기 위해서 적용상의 간편성 때문에 단위유량도는 현재까지도 실무적으로 많이 이용하고 있다.

그러나 유역은 일반적으로 비선형성을 갖는다. 이 때문에 단위유량도의 보완이나 비선형 유출 모형에 관한 연구도 계속되고 있다. 이에 관한 주요 연구를 살펴보면, Minshall (1960)은 단기 강우-유출 자료와 장기 강우 자료를 적용하여 미계측 유역에 적용할 수 있는 단위유량도를 제시하고 강우강도와 단위유량도 첨두치 상관성을 보였다. 그리고 Amorocho and Orlob (1961)는 수문 시스템의 비선형성을 이론적으로 분석하였고 Singh (1964)은 비선형적 순간단위유량도를 제시하였고 Dooge (1967)는 지표 유출에 비선형적인 접근법을 제시하였고 Pilgrim (1976)은 추적자(tracer)를 통하여 홍수 유출의 비선형성을 분석하였다. 또한 Singh (1979)은 3개의 매개변수를 포함하는 비선형적 수문모형을 제시하였고, Rodriguez-Iturbe and Gonzalez-Sanabria (1982)는 비선형 요인으로서 강우 특성에 따라 변동되는 지형학적 순간단위유량도를 제시하였고, Datta and Lettenmaier (1985)은 강우-유출에서 시간 변동성을 고려하는 강우-유출의 비선형성을 연구하였다. 그리고 Singh (1988)은 강우-유출의 비선형적 특성에 관하여 종합적으로 정리하였고 Verde and Cruickshank (1997)은 강우-유출의 비선형성에 관한 물리적인 해석을 제시하였고, Basha (2000)는 단순화한 비선형 강우-유출 모형을 제시하였고 Lallahem and Mania (2003)은 신경망 기술을 이용하여 비선형 강우-유출 모형을 제시하였고 Szilagyi (2007)는 지하수 유동 모형을 적용하여 유출의 비선형성을 분석하였고, Yoo (2010)는 소유역의 강우-유출 관측 자료를 회귀분석 하여 강우강도에 따라 변동되는 단위유량도의 비선형적 특성을 보였다. 그리고 Ding (2011)은 가변적인 순간단위유량도의 비선형적인 특성을 분석하였고 Wu and Wang (2014)은 강우-유출의 비선형 모형을 실용화하기 위한 연구를 수행하였고, Helweg et al. (2021)은 비선형 강우-유출 모형의 매개변수를 효율적으로 계산하는 방법을 제시하였고 Singh (2021)은 비선형적 요인으로서 유역 저류 요인, 하도 저류 요인, 도달시간 등을 포함하는 비선형적 순간단위유량도 이론을 제시하였다. 이 중 본 연구의 주 관심 부분은 Minshall (1960), Singh (1988)와 Yoo (2010) 등에서 연구한 것으로서 강수-유출 분석을 통하여 동일한 유역에서 강수 지속시간이 같더라도 강수 규모가 커지면 단위유량도의 첨두유량은 커지고 첨두발생시간이 빨라지는 비선형적 특성이다. 그러나 이들의 연구에서는 비선형적인 거동의 양상에 대한 물리적인 근거를 제시하거나 규명하는 부분이 부족하였다. 따라서 본 연구는 아직 시도되지 않은 접근법으로서 가상의 유역을 설정하여 강수 규모의 사례 분석을 통하여 강수 규모와 단위유량도 첨두치의 관계, 즉 강수 규모에 따라 첨두치가 변동하는 비선형적인 물리적 거동을 규명하고자 하였다.

1.2 연구 범위 및 제한점

적용상의 편리성으로 인하여 단위유량도 이론(Sherman, 1932)의 연구가 확산하는 가운데 비선형 유출에 관한 연구도 Minshall (1960)의 연구 이후에도 계속됐다. 본 연구에서는 Minshall (1960)에 의하여 제시한 비선형 유출의 연구성과로서 단위유량도의 첨두치가 동일한 유역일지도 강수의 규모가 크면 단위유량도의 첨두치가 커지고 첨두 발생은 빨라지는 연구 결과에 대하여 주목하였다. 그리고 국내 그와 연관된 Yoo (2010)의 연구에서 시험유역의 강수-유출 분석을 통해 얻은 강수 규모와 첨두유량의 관계를 도출한 연구 결과에도 주목하였다. 그러나 앞의 연구들에서는 강수의 세기와 단위유량도 첨두치의 관계식을 얻었지만, 회귀식의 분산이 심하여 신뢰도 있는 함수 관계식을 제시하는 데 한계가 있었다. 이에 본 연구에서는 가상의 유역과 강수 시나리오를 설정하고 수리학적인 분석을 통하여 강수와 단위유량도의 첨두치의 적합한 함수 관계식을 찾아보고자 하였다. 즉 기존 연구들에서 관측된 강우-유출로부터 유도된 단위유량도의 변동은 유역의 강우-유출의 비선형적 특성으로 나타난 것이었다. 이와 같은 비선형적 특성에 영향을 주는 인자는 강우 특성, 유역 저류 특성, 유역 경사 변화 등 매우 복합적이다. 본 연구에서는 강우 특성으로서 강우 규모에 의한 영향만을 규명하는 데 그 초점을 두었다.

본 연구의 결과는 본 연구 목적만을 위해서 단순화한 가상 사례의 연구 결과이므로 본 연구 결과를 이해하고 적용하는데 제한점을 갖는다. 첫째 유역의 경사와 조도는 실제가 아니고 가상의 수치이므로 이에 의해 발생하는 유역의 유하 속도, 거리는 실제와 다소 다를 수 있다. 둘째 가상의 유역에서 강수와 단위유량도의 첨두치와의 함수 관계를 넓게 도출하기 위해서 강수 규모의 크기에 비현실적인 수치가 들어가 있다. 특히 강수 규모에서 500 mm 이상의 비현실적 값이 포함된 것은 넓은 정의역 범위에서의 함수 관계식을 찾기 위한 것이므로 이는 본 연구를 이해하는데 국한하며 실무적 사용에는 제한적임을 밝힙니다. 그리고 본 연구에서 10개 순간 강수의 시나리오에서 제시한 유역 유출과 단위유량도의 산출 과정을 모두 제시한 것은 강수의 크기에 따라 단위유량도의 첨두치가 비선형적으로 어떻게 거동하는지를 보여 주기 위함이다.

2. 연구 방법 및 과정

일반적으로 복잡한 문제를 풀기 위해서는 단순화하면 그 해법을 찾을 수 있다. 복합적인 요인을 갖는 강수-유출의 비선형성을 포함하는 단위유량도의 변동성과 강수 특성과의 관계를 규명하기 위해서는 단순화하여 분석하는 것이 필요하다. 따라서 본 연구에서도 대상 유역과 강수-유출을 단순화하여 접근하였다. 이를 위한 본 연구 과정은 Fig. 1과 같다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F1.jpg

Fig. 1.

Process of this study

2.1 접근 방법

본 연구에서는 대상 유역을 단순화한 가상의 유역과 강수 시나리오를 설정하고 수리학적인 분석을 통하여 강수 규모와 단위유량도 첨두치의 적합한 함수 관계를 규명하고자 하였다. 이를 위해서 단위유량도를 산출하는 방법은 수문학에서 유역 유출을 기초적으로 이해하기 위한 이론으로 이용되는 시간-면적(Time-Area) 방법이다. 이 방법에 따르면 유역의 등유하선(isochromes) 사이의 유역의 분할 면적으로 시간별 막대그래프(histogram)를 구하고 이것과 유효강수 주상도(hyetograph)에 대하여 이산 회선적분(discrete convolution integration)을 취하여 직접유출량을 산출할 수 있다(Singh, 1988). 따라서 여기서 시간별 막대그래프는 단위유량도 이론의 이산적 단위유량도(discrete unit hydrograph)로 취급할 수 있다. 이 방법은 유역의 저류(Storage) 특성을 고려하지 않는 방법이다.

2.2 기본 설정

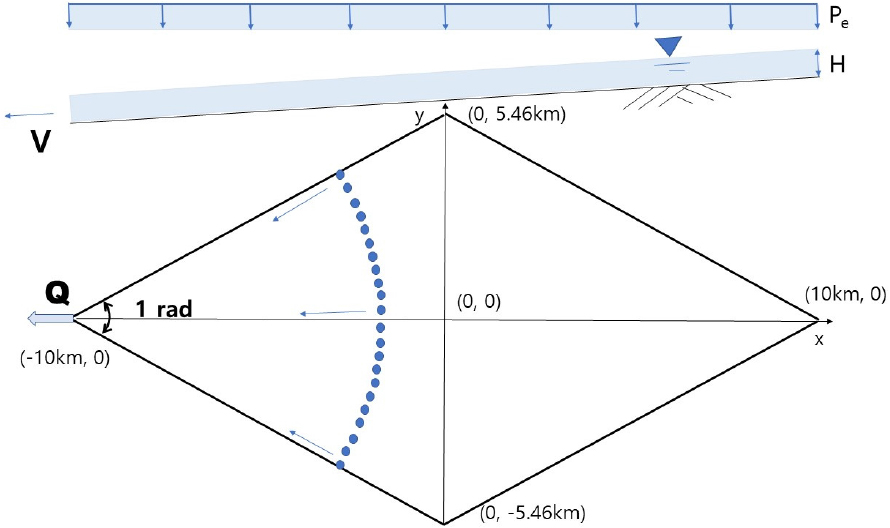
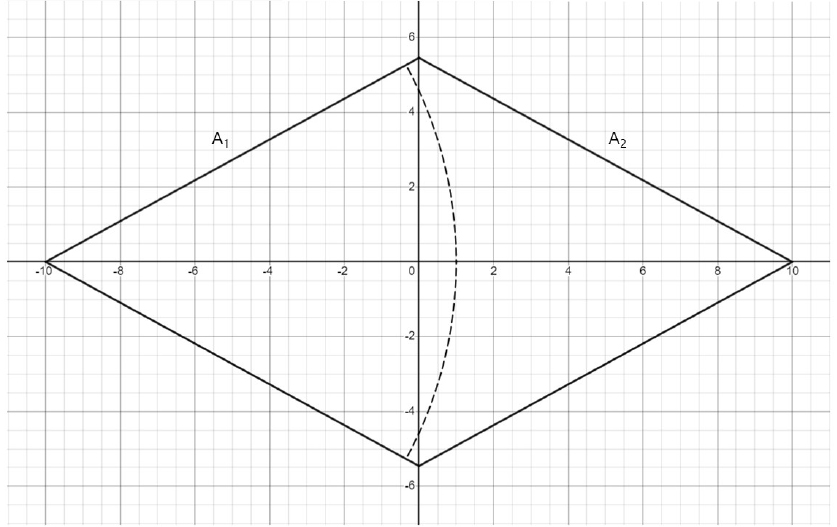
본 연구 목적을 달성하기 위해서 몇 가지의 가정 사항을 설정하였다. 첫 번째로 적용한 강수는 순간 강수(instantaneous precipitation)로 침투 등의 손실이 제거된 유효강수이고 두 번째로 유역의 강수에 의한 유출수는 출구 방향으로 직선적으로 유출된다. 그리고 세 번째로 유역의 형태는 한 변의 길이가 11.39 km이고 면적이 109.2 km²인 마름모형이고 마름모 출구 쪽의 내각은 1rad이다. 네 번째로 유역의 경사는 1/100로 일정하다고 가정하였고 다섯 번째로 유출은 등류의 개수로 흐름으로 가정하였고 여섯 번째로 유역의 조도(roughness)는 일정하다고 가정하여 계산 편의상 Chezy 유속 계수는 27.8 $\sqrt{m} / s$ 로 고정하였다. 이와 같은 가상의 유역은 연구 편의상 다음 Fig. 2와 같이 x-y 좌표평면에 설정하였다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F2.jpg

Fig. 2.

Schematic of watershed applied for effective precipitation (P_e) and direct runoff (Q) in x-y coordinates

2.3 강수 규모 사례 설정

본 연구에서는 앞서 설정한 유역에서 단위유량도를 산출하는데 직접유출량(direct runoff)을 대상으로 하므로 적용하는 강수는 유효강수(effective precipitation)를 의미한다. 본 연구는 강수의 규모를 10가지 사례로서 10 mm, 40 mm, 90 mm, 160 mm, 250 mm, 360 mm, 640 mm, 1,000 mm, 1,210 mm, 1,690 mm의 경우로 설정하였다.

2.4 강수 규모별 사례 연구

Fig. 2에서 강수 규모( $P_{e}$ )는 강수 깊이로서 유역에서 유출되는 등류 수심 H와 같다고 보았다. 이 경우 유역 수로에서 적합한 Chezy의 유속 공식(Chow, 1959; French, 1986)인 Eq. (1)을 적용하여 유출 속도(m/s)를 산출한다. Eq. (1)은 등류 흐름(uniform flow)의 평균유속공식으로서 C는 경사면 상태를 나타내는 Chezy의 평균유속 계수( $\sqrt{m} / s$ )로 본 연구에서는 편의상의 값 27.8 $\sqrt{m} / s$ 을 적용하였고 I는 유역의 경사로 1/100을 적용하였다. 그리고 R은 경심으로서 유역 유출에서는 수심과 동일하므로 순간 강수량 $P_{e}$ (m)과 같도록 적용하였다.

(1)

V = C \sqrt{R I}

따라서 유출 속도는 $V = 27.8 \sqrt{m} / s \times \sqrt{P_{e} \times \frac{1}{100}}$ =2.78 $\times \sqrt{P_{e}} m / s = 10 \times \sqrt{P_{e}} km / hr$ 이 되고 유역에서 유하 속도가 된다. 강수 규모별로 유하 시간과 시간당 유하 거리를 산출하면 Table 1과 같다. 이것은 시간-면적(Time-Area) 방법을 적용하기 위해서 산출된 값이다. 강수 규모별 시간당 유하 거리(Travel distance per hour)는 대상 유역에 등유하시간선 사이의 거리를 나타낸다.

Table 1.

Runoff velocity and travel distance per hour by precipitation

Precipitation (mm)	Runoff Velocity (m/s)	Travel distance per hour (km)
10	0.278	1
40	0.556	2
90	0.834	3
160	1.11	4
250	1.39	5
360	1.67	6
640	2.22	8
1,000	2.78	10
1,210	3.06	11
1,690	3.61	13

2.4.1 10 mm의 경우

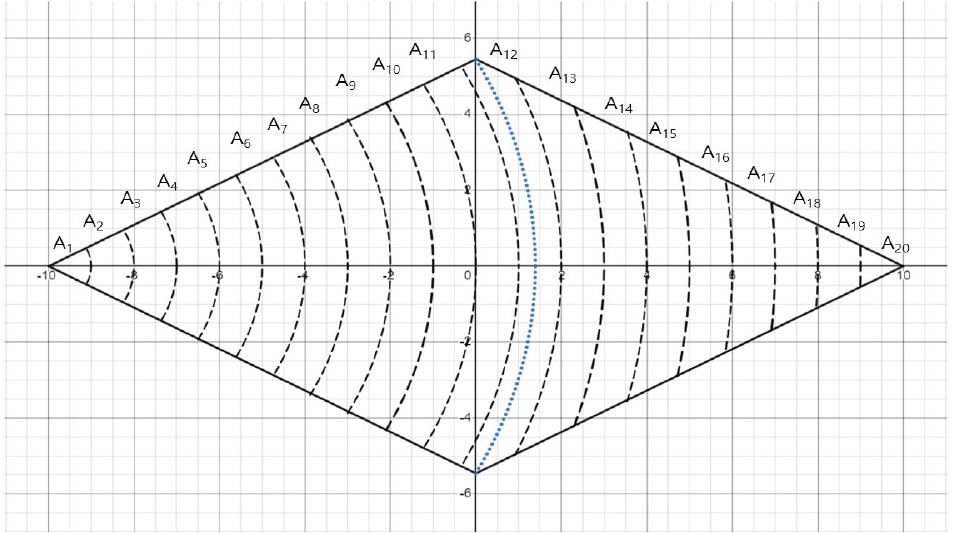
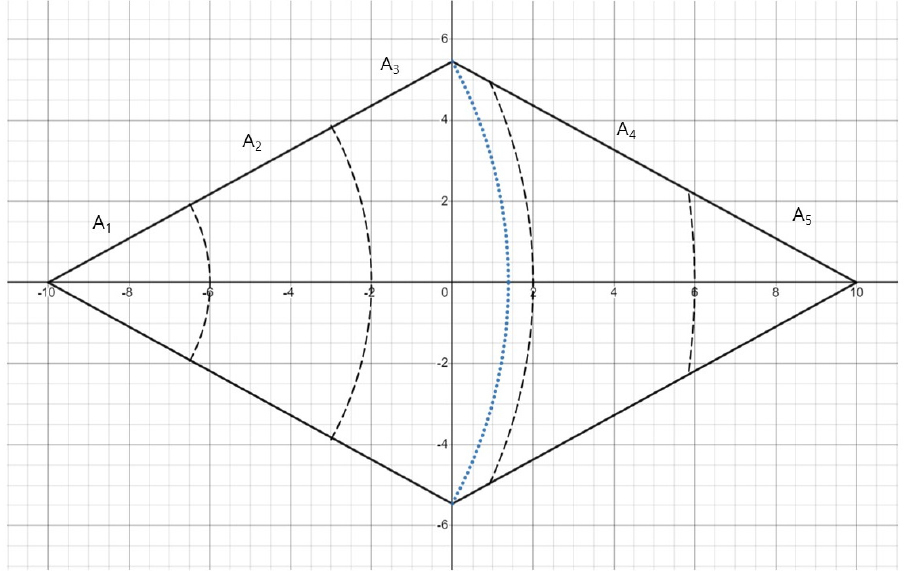
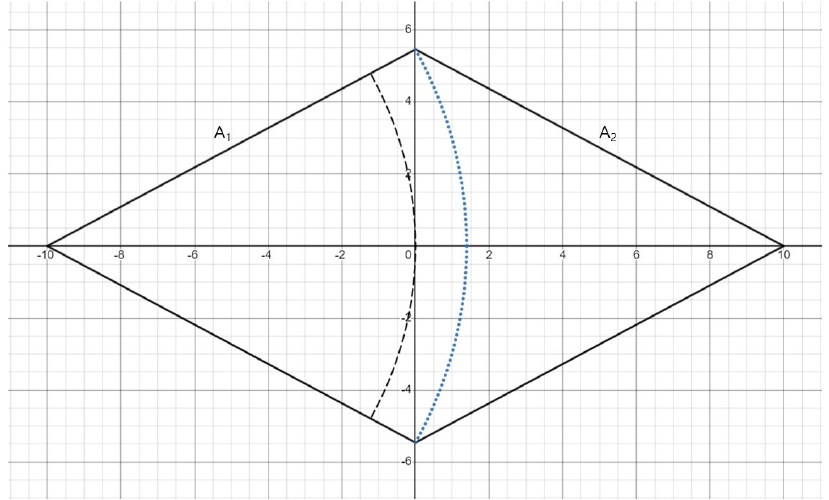
10 mm의 경우 설정된 마름모 유역에 1시간 간격으로 유역 출구로부터 등유하선(isochromes)은 Fig. 3에서와 같이 점선으로 표시할 수 있다. 이 유역도와 등유하선은 상용앱 DESMOS의 x-y 좌표에 도시한 것이다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F3.jpg

Fig. 3.

Watershed with dotted isochrome lines and travel area ( $A_{i}$ ) per hour in x-y coordinates in case of 10 mm precipitation

Fig. 3에서 검은색 점선 사이에 흘러내리는 시간은 1시간이고 거리 간격은 1 km이다. 유역 유출의 출구 위치는 유역의 최저점으로서 좌표상(-10, 0) 이고 유역의 최고점은 좌표상(10, 0)이다. 그리고 10 mm의 강수 $P_{e}$ 가 유역에 순간적으로 발생하면 유역 출구 지점에서 1시간 간격으로 유출되는 유출량 $Q_{i}$ 는 $i$ 시간(hour) 동안 유출되는 유량이다. 그리고 $A_{i} (k m^{2})$ 는 전체 유역에 순간 강수가 발생한 후에 $i$ 시간(hour)이 지나면 유역의 출구를 통과하는 유출되는 유역의 면적이다. $Q_{i}$ (10⁶m³)는 Eq. (2)와 같이 $i$ 시간(hour) 동안의 유출 면적 $A_{i}$ (10⁶m²)에 강수 깊이( $P_{e}$ ) 값인 0.01m를 곱한 양이 된다.

(2)

Q_{i} = P_{e} A_{i}

이렇게 구한 시간별 유출량을 유출량 총량으로 나눈 단위유량도의 종거값(무차원)은 Table 2와 같이 계산하였다. 여기서 면적 $A_{i}$ 값은 등유하선 간의 적분을 통하여 산출하였다.

Table 2.

Calculation of runoff and unit hydrograph of 10 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	0.5	0.01	0.0050	0.0046
2	1.5	0.01	0.0150	0.0137
3	2.5	0.01	0.0250	0.0229
4	3.5	0.01	0.0350	0.0321
5	4.5	0.01	0.0450	0.0412
6	5.5	0.01	0.0550	0.0504
7	6.5	0.01	0.0650	0.0595
8	7.5	0.01	0.0750	0.0687
9	8.5	0.01	0.0850	0.0778
10	9.5	0.01	0.0950	0.0870
11	10.5	0.01	0.1050	0.0962
12	13.3	0.01	0.1327	0.1216
13	8.2	0.01	0.0815	0.0747
14	7.2	0.01	0.0715	0.0655
15	6.1	0.01	0.0611	0.0559
16	5.0	0.01	0.0503	0.0460
17	3.9	0.01	0.0393	0.0360
18	2.8	0.01	0.0281	0.0257
19	1.7	0.01	0.0169	0.0155
20	0.6	0.01	0.0056	0.0052
Total	109.2	0.01	1.0920	1.0000

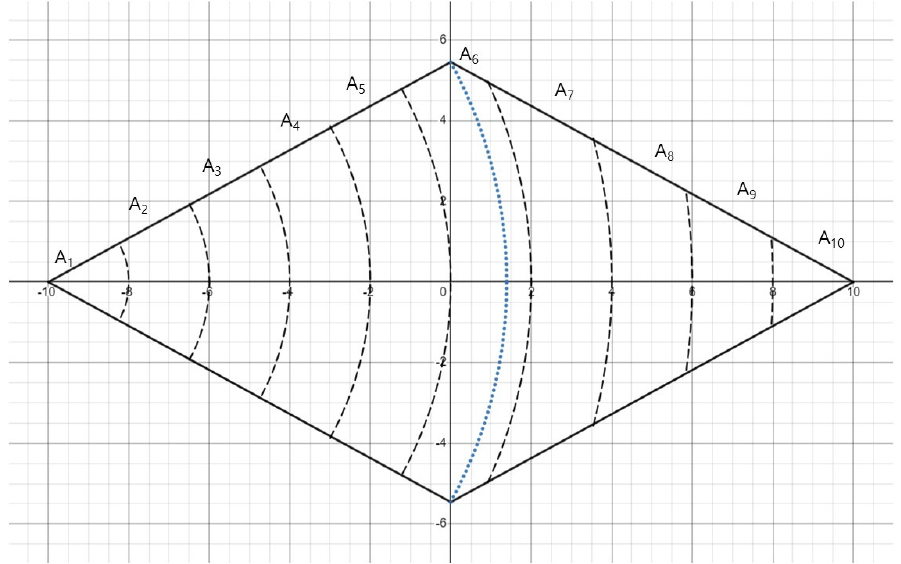
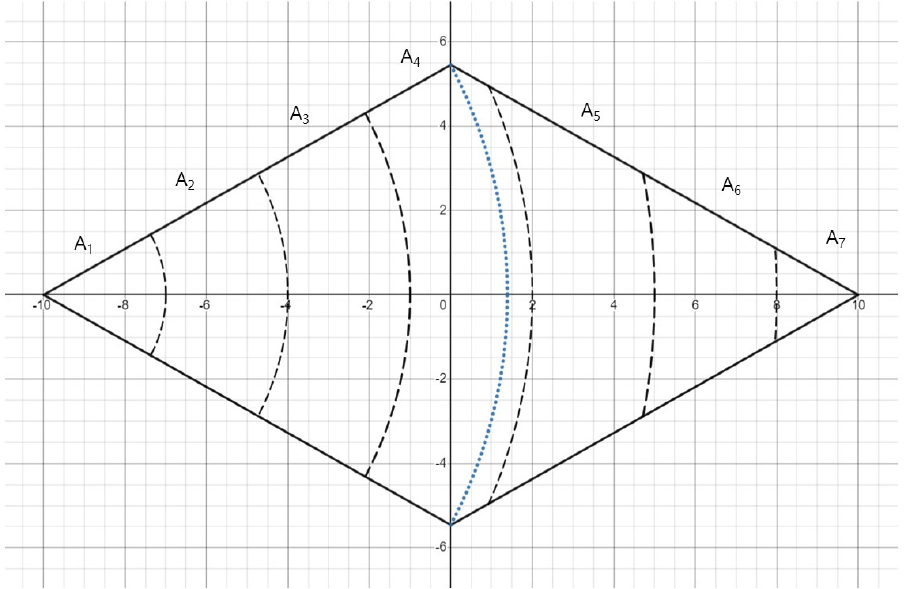
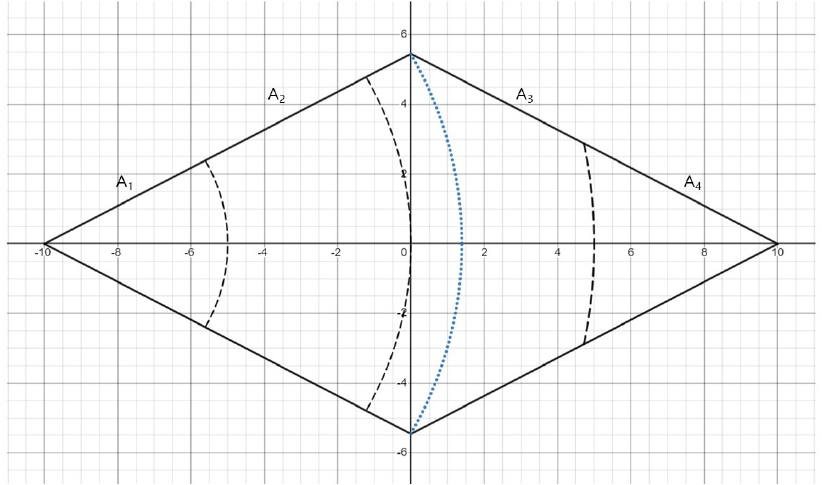
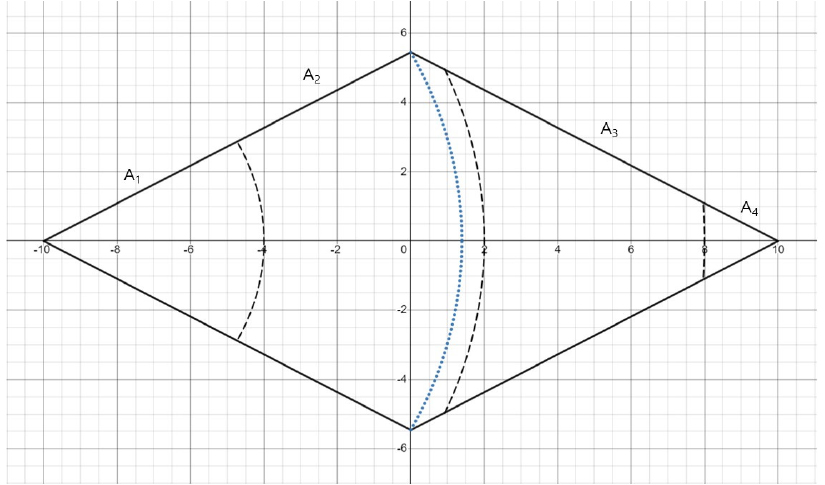
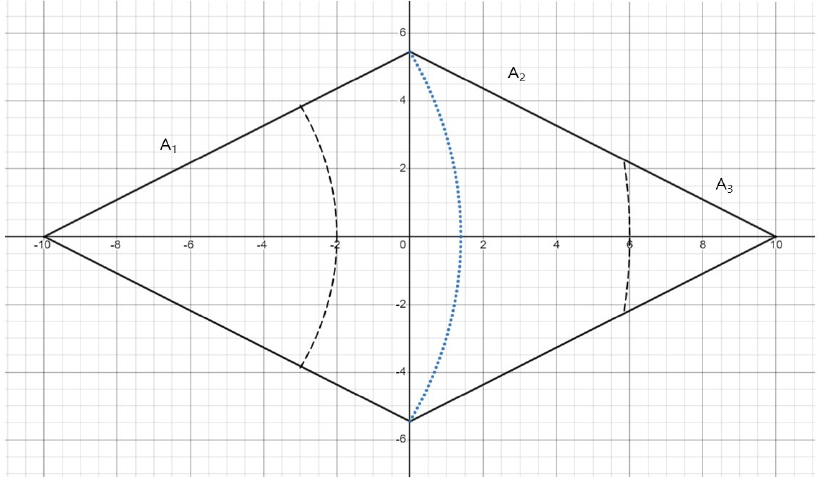
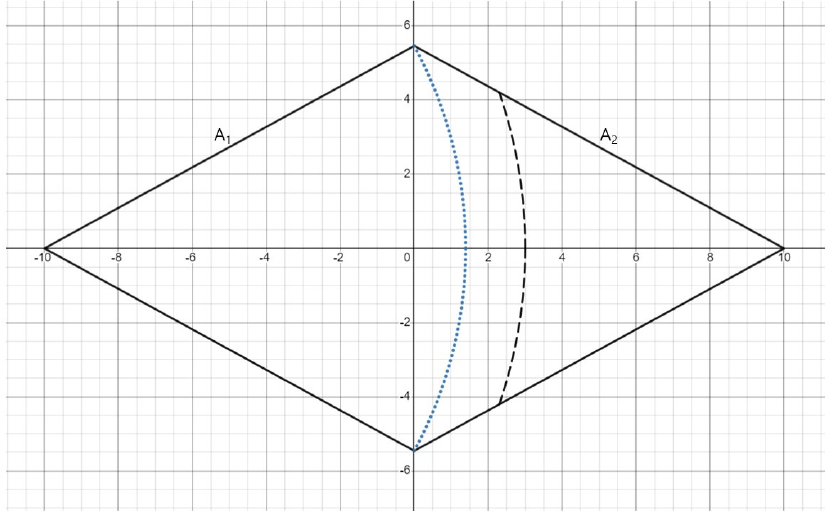
10 mm의 경우와 같은 방법과 과정으로 강수 규모 40 mm, 90 mm, 160 mm, 250 mm, 360 mm, 640 mm, 1,000 mm, 1,210 mm, 1,690 mm의 경우에 적용한 결과는 다음 2.4.2~2.4.10 항목의 Figs. 4~12 및 Tables 3~11과 같다.

2.4.2 40 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F4.jpg

Fig. 4.

Same as Fig. 3 in case of 40 mm precipitation

Table 3.

Calculation of runoff and unit hydrograph of 40 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	2.0	0.04	0.080	0.01832
2	6.0	0.04	0.240	0.05495
3	10.0	0.04	0.400	0.09158
4	14.0	0.04	0.560	0.12821
5	18.0	0.04	0.720	0.16484
6	20.8	0.04	0.830	0.19009
7	16.6	0.04	0.664	0.15212
8	12.1	0.04	0.483	0.11062
9	7.3	0.04	0.292	0.06693
10	2.4	0.04	0.098	0.02236
Total	109.2	0.04	4.368	1.00000

2.4.3 90 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F5.jpg

Fig. 5.

Same as Fig. 3 in case of 90 mm precipitation

Table 4.

Calculation of runoff and unit hydrograph of 90 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	4.5	0.09	0.405	0.04121
2	13.5	0.09	1.215	0.12363
3	22.5	0.09	2.025	0.20604
4	30.3	0.09	2.723	0.27704
5	23.2	0.09	2.092	0.21289
6	12.8	0.09	1.148	0.11685
7	2.4	0.09	0.220	0.02234
Total	109.2	0.09	9.828	1.00000

2.4.4 160 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F6.jpg

Fig. 6.

Same as Fig. 3 in case of 160 mm precipitation

Table 5.

Calculation of runoff and unit hydrograph of 160 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	8.0	0.16	1.280	0.07326
2	24.0	0.16	3.840	0.21978
3	38.7	0.16	6.199	0.35481
4	28.7	0.16	4.594	0.26294
5	9.7	0.16	1.559	0.08921
Total	109.2	0.16	17.472	1.00000

2.4.5 250 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F7.jpg

Fig. 7.

Same as Fig. 3 in case of 250 mm precipitation

Table 6.

Calculation of runoff and unit hydrograph of 250 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	12.5	0.25	3.125	0.11447
2	37.5	0.25	9.375	0.34341
3	44.0	0.25	11.000	0.40292
4	15.2	0.25	3.800	0.13920
Total	109.2	0.25	27.300	1.00000

2.4.6 360 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F8.jpg

Fig. 8.

Same as Fig. 3 in case of 360 mm precipitation

Table 7.

Calculation of runoff and unit hydrograph of 360 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	18.0	0.36	6.480	0.16484
2	52.7	0.36	18.982	0.48285
3	36.0	0.36	12.976	0.33008
4	2.4	0.36	0.874	0.02224
Total	109.2	0.36	39.312	1.00000

2.4.7 640 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F9.jpg

Fig. 9.

Same as Fig. 3 in case of 640 mm precipitation

Table 8.

Calculation of runoff and unit hydrograph of 640 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	32.0	0.64	20.480	0.29304
2	69.5	0.64	44.477	0.63641
3	7.7	0.64	4.931	0.07055
Total	109.2	0.64	69.888	1.00000

2.4.8 1,000 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F10.jpg

Fig. 10.

Same as Fig. 3 in case of 1,000 mm precipitation

Table 9.

Calculation of runoff and unit hydrograph of 1,000 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	50.0	1.00	50.000	0.45788
2	59.2	1.00	59.200	0.54212
Total	109.2	1.00	109.200	1.00000

2.4.9 1,210 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F11.jpg

Fig. 11.

Same as Fig. 3 in case of 1,210 mm precipitation

Table 10.

Calculation of runoff and unit hydrograph of 1,210 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	60.5	1.21	73.205	0.55403
2	48.7	1.21	58.927	0.44597
Total	109.2	1.21	132.132	1.00000

2.4.10 1,690 mm의 경우

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F12.jpg

Fig. 12.

Same as Fig. 3 in case of 1,690 mm precipitation

Table 11.

Calculation of runoff and unit hydrograph of 1,690 mm precipitation

Time ( $i$ ) hr	Area ( $A_{i}$ ) Km²(10⁶m²)	Precipitation ( $P_{e}$ ) m	Runoff ( $Q_{i}$ ) 10⁶m³(MCM)	Unit hydrograph
1	83.8	1.69	141.593	0.76724
2	25.4	1.69	42.955	0.23276
Total	109.2	1.69	184.548	1.00000

3. 연구 결과 및 분석

3.1 강수 규모별 단위유량도

강수 규모별로 단위유량도를 산출한 결과를 도시하면 Fig. 13과 같다. Fig. 13에서 보는 바와 같이 대체로 강수 규모가 커질수록 단위유량도는 첨두치는 커지고 발생 시간도 짧아지는 특성을 보였다. 일부 경우에서 유역의 형상과 순간 강수로 인해 분산이 나타났지만 대체로 강수량이 많아지면 유하 속도도 커지고 이에 따라 시간당 유하 거리와 면적도 커지므로 단위유량도의 앞부분 즉 첨두유량이 커지고 빨라지게 된다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F13.jpg

Fig. 13.

Unit hydrographs calculated for 40 mm, 90 mm, 160 mm, 250 mm, 360 mm, 640 mm, 1,000 mm, 1,210 mm and 1,690 mm precipitation

3.2 강수 규모별 단위유량도의 첨두유량과 첨두발생시간

강수 규모별 단위유량도의 첨두유량과 첨두발생시간을 추출하여 정리하면 Table 12와 같다. Table 12에서 보는 바와 같이 강수 규모가 커지면 첨두유량 값이 커지고 첨두발생시간은 작아지는 것을 보였다.

Table 12.

Peak flow and time to peak of unit hydrograph by precipitation

Precipitation (mm)	Peak flow (dimensionless)	Time to peak (hr)
10	0.12155	12
40	0.19009	6
90	0.27704	4
160	0.35481	3
250	0.40292	3
360	0.48285	2
640	0.63641	2
1,000	0.54213	2
1,210	0.55403	1
1,690	0.76724	1

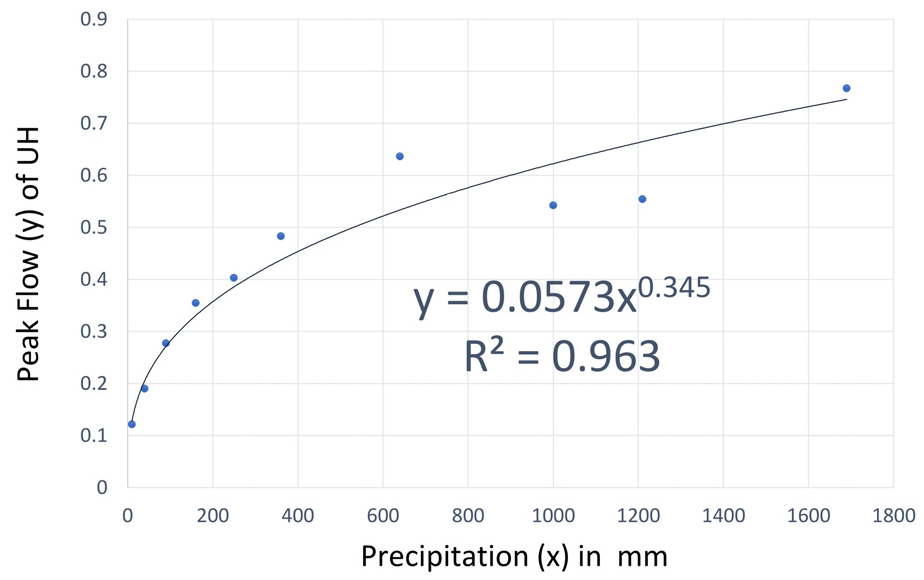
3.3 강수 규모와 단위유량도 첨두유량의 관계 분석

강수 규모와 단위유량도의 첨두유량을 도시하면 Fig. 14와 같다. Fig. 14와 같이 강수 규모가 클수록 첨두유량도 커지는 경향을 보였다. MS Office Excel에서 선택한 지수형 추세선의 회귀(regression)식은 다음 Eq. (3)과 같다. 여기서 결정계수 $R^{2}$ 은 일치하는 정도로서 0과 1 사잇값이다. Eq. (3)의 $Q_{p}$ 은 단위유량도의 첨두유량(무차원)이고 $P_{e}$ 은 유효강수의 규모(mm)를 나타낸다. 이때 결정계수 $R^{2}$ 값은 0.963 정도이었다. 산출된 결정계수는 높지만 Fig. 13에서 강수가 1,000 mm, 1,210 mm일 때 분산을 보이는 이유는 적용한 유역의 형상과 순간 강수의 유출 특성에 의하여 나타난 물리적 양상이다.

(3)

Q_{p} = 0.0573 P_{c}^{0.345}

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F14.jpg

Fig. 14.

Relationship between precipitation scale and peak flow of unit hydograph

3.4 강수 규모와 단위유량도 첨두발생시간의 관계 분석

강수 규모와 단위유량도의 첨두발생시간을 도시하면 Fig. 15와 같다. Fig. 15와 같이 강수 규모가 클수록 단위유량도의 첨두유량이 일찍 발생하는 경향을 보였다. Excel에서 선택한 지수형 추세선의 회귀식은 다음 Eq. (4)와 같다. Eq. (4)의 $T_{p}$ 은 단위유량도의 첨두발생시간(hr)이고 $P_{e}$ 은 유효강수의 규모(mm)를 나타낸다. 이때 결정계수( $R^{2}$ ) 값은 0.951 정도이었다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F15.jpg

Fig. 15.

Relationship between precipitation scale and time to peak of unit hydrograph

(4)

T_{p} = 33.2 P_{e}^{- 0.457}

3.5 단위유량도의 첨두유량에 따른 첨두발생시간 관계 분석

Eqs. (3) and (4)에 의하면 단위유량도의 첨두유량에 따른 첨두발생시간의 관계식은 Eq. (5)와 같다. 기존의 다른 연구(Laurenson, 1964)와 비교할 목적으로 Eq. (5)의 $Q_{p}$ 의 차원(단위)은 앞서와 달리 무차원에서 mm/hr로 전환한 것이다.

(5)

T_{p} = 12.6 Q_{p}^{- 0.340}

Laurenson (1964)의 연구에서는 89.6 km² 규모의 South Creek 유역의 23개 강우-유출 사상을 분석하여 지체시간( $T_{L}$ : 유효강우와 직접유출 수문곡선의 각 중심점 사이 시간)과 직접유출의 규모로서 평균 유출량( $Q_{m}$ in mm/hr)의 관계식을 Eq. (6)과 같이 나타내었다.

(6)

T_{L} = 10.3 Q_{m}^{- 0.270}

기존 연구(Laurenson, 1964)의 결과와 본 연구성과를 비교하기 위해서 순간 강우와 삼각형 형상의 단위유량도를 고려하여 Eq. (5)의 첨두발생시간 $T_{p}$ 와 지체시간 $T_{L}$ 와 동일시하고 $Q_{p} = 2 Q_{m}$ 이라 하면 Eq. (5)는 Eq. (7)로 변경된다.

(7)

T_{L} = 9.95 Q_{m}^{- 0.340}

본 연구의 결과로부터 얻은 Eq. (7)과 기존 연구의 성과인 Eq. (6)은 유사한 관계를 보였다.

3.6 기존 연구와 본 연구성과 비교

본 연구에서 강수 규모와 단위유량도의 첨두유량의 관계식과 강수 규모와 단위유량도의 첨두발생시간의 관계식을 회귀 분석하면서 강수 규모의 수는 비록 통계적으론 적은 양이지만 비선형성을 갖는 첨두치 거동의 양상을 확인할 수 있는 좋은 성과이다. 본 연구의 성과는 기존 연구(Minshall, 1960; Yoo, 2010)에서 분석한 실제 시험유역의 성과와 Table 13과 같이 비교될 수 있다. 여기서 기존 연구와의 비교를 위해서 앞서 표기한 $P_{e}$ (유효강우량)를 R이라 표기하였고 앞서 3.5절과 같은 내용과 동등하게 분석하였다. 비교된 2개의 기존 연구에 적용한 대상 유역은 각각 Figs. 16 and 17과 같다. 기존 연구(Yoo, 2010)에 적용한 유역은 한강권에 속한 임진강의 지류인 설마천의 중류부에 위치하고 8.5 km² 규모이고 평균 경사가 20% 정도 되는 대부분 산림지로 되어 있는 전적비교 유역(Fig. 16)이었고 또 다른 Minshall (1960)의 적용 유역은 미국 일리노이주의 Edwardsville watershed는 0.110 km² 크기를 갖고 있고 전체 유역 2/3의 경사가 1% 이내이고 대부분 경작지와 초지로 구성된 소규모 실험 유역(Fig. 17)이다. 유역의 형상은 두 개 모두 다이아몬드 형태의 모양으로 본 연구 대상인 유역 형상인 마름모와 유사한 형상을 하였다.

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F16.jpg

Fig. 16.

Seolmacheon watershed, Paju, Kyeonggi, South Korea (Yoo, 2010; area size = 8.5 km², average slope is about 20%, and it’s mostly forested)

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F17.jpg

Fig. 17.

Edwardsville watershed, Illinois, US (Minshall, 1960; area size = 0.110 km², two-thirds of area slope is less than 1%, and it’s mostly cultivated and in legume hay)

본 연구는 가상의 유역을 대상으로 하였지만 본 연구에서 얻은 관계식은 실제 유역으로부터 얻은 기존 연구성과의 관계식과 유사한 멱함수 관계를 보였다. 여기서 지체시간( $T_{L}$ )과 평균 유출량( $Q_{m}$ )의 관계식은 다음 Eq. (7)과 같은 멱함수로 표현할 수 있다.

(8)

T_{L} = a Q_{m}^{- b}

그리고 Table 13의 $T_{L}$ 와 $Q_{m}$ 의 관계식에서 지숫값(b in Eq. (7) )을 비교해 보면 본 연구의 가상 유역은 저류 효과가 없으므로 본 대상 유역에서 유출량 증가에 따라 첨두발생시간이나 지체시간의 감소율이 기존 연구의 실제 유역에서의 감소율보다 더 작게 나타난 것으로 해석된다. 그리고 지체시간( $T_{L}$ )의 절대 크기를 좌우하는 $Q_{m}$ 항의 앞에 곱해진 계수 값(a in Eq. (7) )은 Fig. 18과 같이 유역면적의 크기에 잘 비례하는 것으로 나타났다. 이는 저류 효과가 없는 가상의 유역에서의 유출도 비선형 유출의 특성을 보여 주고 있다는 물리적으로도 유의미한 특성을 보여 주었다.

Table 13.

Comparison of the results of previous studies and this study

Category		Watershed area size (km²)	$Q_{p}$ , Peak Flow	$T_{p}$ , Time to peak	$T_{p}$ and $Q_{p}$	remark
					$T_{L}$ and $Q_{m}$
This study		109.2	$Q_{p} = 0.0573 R^{1.345}$	$T_{p} = 33.2 R^{- 0.457}$	$T_{p} = 12.6 Q_{p}^{- 0.340}$	$Q_{p}$ in mm/hr, $Q_{m} = \frac{Q_{p}}{2}$ $T_{p} ≑ T_{L}$ in hour, $R$ in mm/hr
					$T_{L} = 9.95 Q_{m}^{- 0.340}$
Previous studies	Minshall (1960)	0.110	$Q_{p} = 1.74 R^{0.779}$	$T_{p} = 0.413 R^{- 0.564}$	$T_{p} = 0.584 Q_{p}^{- 0.706}$
					$T_{L} = 0.358 Q_{m}^{- 0.706}$
	Yoo (2010)	8.5	$Q_{p} = 0.0483 R^{1.26}$	$T_{p} = 16.7 R^{- 0.724}$	$T_{p} = 2.93 Q_{p}^{- 0.576}$
					$T_{L} = 1.96 Q_{m}^{- 0.576}$

https://cdn.apub.kr/journalsite/sites/kwra/2023-056-10/N0200561005/images/kwra_56_10_05_F18.jpg

Fig. 18.

Relationship between Q_m(Average Discharge) in mm/hr and T_L(Lag Time) in hour to compare this result with previous studies (Minshall, 1960; Yoo, 2010)

4. 주요 연구 결과 및 결론

본 연구에서는 강수 규모가 단위유량도 첨두치에 주는 영향을 규명하기 위해서 유역을 단순화한 마름모형 유역에서 10가지 규모의 순간적 강수에 대하여 발생한 단위유량도 첨두유량의 관계와 첨두발생시간의 관계를 각각 산출하였다. 이때 유역에 내린 강수는 유효강수량이고 유출은 직접유출이고 낙하지점에서 출구 방향으로 직선적인 등류로 유출된다고 가정하였다. 이에 따라 일정 강수 규모일 때 유역에서 유출되는 유속은 유역 전체에서 등류 상태로 일정하게 보고 등류 평균유속공식인 Chezy 공식에 의하여 산출하였다. 순간 강수 규모는 10가지로 유효강수 10 mm, 40 mm, 90 mm, 160 mm, 250 mm, 360 mm, 640 mm, 1,000 mm, 1,210 mm, 1,690 mm인 경우에 대하여 단위유량도의 첨두유량과 첨두발생시간을 각각의 관계를 산출하였다. 강수 규모( $P_{e}$ )에 대하여 단위유량도의 첨두유량( $Q_{p}$ )의 관계는 $Q_{p} = 0.0573 P_{e}^{0.345}$ 이었고 첨두발생시간( $T_{p}$ )의 관계는 $T_{p} = 33.2 P_{e}^{- 0.457}$ 이었고 $T_{p} = 12.6 Q_{p}^{- 0.340}$ 의 관계를 보였다.

본 연구에서는 강수 규모만이 첨두유량의 크기와 발생 시간에 미치는 효과를 얻기 위해서 대상 유역을 마름모 형태, 일정 경사, 일정 조도를 갖고 저류 효과를 고려하지 않는 가상 유역의 환경 상태로 단순화하였다. 이로부터 얻은 구체적 성과는 강수 규모가 커질수록 유출 깊이가 커져서 유역의 유속이 빨라지고 단위 시간당 유하 거리도 커지므로 첨두유량은 커지고 첨두발생시간은 빨라진다는 것이었다. 그리고 주목할 점은 저류 효과를 고려하지 않아도 유역에서 유출이 비선형적 특성을 보였다는 것이다. 실제 유역에서 실험적으로 얻은 기존 연구의 성과들과 본 연구성과의 비교를 통하여 가상 유역 상의 본 연구성과가 실제 유역에서의 기존 연구의 성과와도 어느 정도 물리적으로 부합되는 것과 강수 규모가 첨두유량과 첨두발생시간에 미치는 비선형적인 영향을 확인할 수 있었다.

Acknowledgements

본 연구는 2017년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행한 이공학개인기초연구(2017R1D1A3B03035695) 및 2022년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(NRF-2022R1I1A1A01056269)의 일환으로 수행되었음.

Conflicts of Interest

The authors declare no conflict of interest.

References

Amorocho, J., and Orlob, G.T. (1961). Nonlinear analysis of hydrologic systems. Water Resources Center Contribution 40, University of California, Berkeley, CA, U.S.

Basha, H.A. (2000). "Simple nonlinear rainfall-runoff model." Journal of Hydrologic Engineering, Vol. 5, No. 1, pp. 25-32. 10.1061/(ASCE)1084-0699(2000)5:1(25)

Chow, V.T. (1959). Open-channel hydraulics. International student edition, McGraw-Hill, New York, NY, U.S.

Datta, B., and Lettenmaier, D.P. (1985). "A nonlinear time-variant constrained model for rainfall-runoff." Journal of Hydrology, Vol. 77, No. 1/4, pp. 1-18. 10.1016/0022-1694(85)90194-5

Ding, J.Y. (2011). "A measure of watershed nonlinearity: Interpreting a variable instantaneous unit hydrograph model on two vastly different sized watersheds." Hydrology and Earth System Sciences, Vol. 15, No. 1, pp. 405-423. 10.5194/hess-15-405-2011

Dooge, J.C.I. (1967). "A new approach to nonlinear problems in surface water hydrology: Hydrologic system with uniform nonlinearity." International Association of Scientific Hydrology Publication, Vol. 76, pp. 409-413.

French, R.H. (1986). Open-channel hydraulics. International editions, Civil engineering series, McGraw-Hill, New York, NY, U.S.

Helweg, O.J., Amorocho, J., and Finch, R.H. (2021). "Improvement of nonlinear rainfall-runoff model." Journal of the Hydraulics Division, Vol. 108, No. 7, pp. 813-822. 10.1061/JYCEAJ.0005882

Lallahem, S., and Mania, J. (2003). "A nonlinear rainfall-runoff model using neural network technique: example in fractured porous media." Mathematical and Computer Modelling, Vol. 37, No. 9/10, pp. 1047-1061. 10.1016/S0895-7177(03)00117-1

Laurenson, E.M. (1964). "A catchment storage model for runoff routing." Journal of Hydrology, Vol. 2, No. 2, pp. 141-163. 10.1016/0022-1694(64)90025-3

Minshall, N.E. (1960). "Predicting storm runoff on small experimental watersheds." Journal of the hydraulics Division, Proceedings of ASCE, Vol. 86, No. HY8, pp. 17-38. 10.1061/JYCEAJ.0000509

Pilgrim, D.H. (1976). "Travel times and nonlinearity of flood runoff from tracer measurements on a small watershed." Water Resources Research, Vol. 12, No. 3, pp. 487-496. 10.1029/WR012i003p00487

Rodriguez-Iturbe, I., and Gonzalez-Sanabria, M. (1982). "A geomorphoclimatic theory of the instantaneous unit hydrograph." Water Resources Research, Vol. 18, No. 4, pp. 877-886. 10.1029/WR018i004p00877

Sherman, L.K. (1932). "Stream flow from rainfall by the unit graph method." Engineering News-Record, Vol. 108, pp. 501-505.

Singh, K.P. (1964). "Nonlinear instantaneous unit hydrograph theory." Journal of the Hydraulics Division, Proceedings of ASCE, Vol. 90, No. HY2, pp. 313-347. 10.1061/JYCEAJ.0001020

Singh, K.P. (2021). "Nonlinear instantaneous unit-hydrograph theory." Journal of the Hydraulics Division, Vol. 90, No. 2, pp. 313-347. 10.1061/JYCEAJ.0001020

Singh, V.P. (1979). "A uniformly nonlinear hydrologic cascade model." Irrigation and Power, Vol. 36, No. 3, pp. 301-317.

Singh, V.P. (1988). Hydrologic systems, rainfall-runoff modeling vol. I. Prentice-Hall, Hoboken, NJ, U.S.

Szilagyi, J. (2007). "Analysis of the nonlinearity in the hillslope runoff response to precipitation through numerical modeling." Journal of Hydrology, Vol. 337, No. 3-4, pp. 391-401. 10.1016/j.jhydrol.2007.02.005

Verde, C., and Cruickshank, C. (1997). "Structure of rainfall-runoff nonlinear model with physical interpretation." Mathematical Modelling, pp. 737-742.

Wu, P.L., and Wang, H.J. (2014). "Expounding the application of analysis method about nonlinear hydrological system of rainfall-runoff." Advanced Materials Research, Vol. 1065-1069, No. 59, pp. 2964-2969. 10.4028/www.scientific.net/AMR.1065-1069.2964

Yoo, J.H. (2010). "An offer of relation between rainfall and unit hydrograph in a small basin." Journal of Korean Water Resources Association, Vol. 43, No. 7, pp. 635-643. 10.3741/JKWRA.2010.43.7.635

Journal of Korea Water Resources Association 한국수자원학회 논문집 ISSN:2799-8746(Print) 2799-8754(Online)

Preview

Identification of unit hydrograph peak behavior according to changes in precipitation scale in a virtual watershed

ABSTRACT

MAIN

Fig. 1.

Process of this study

Fig. 2.

Schematic of watershed applied for effective precipitation (Pe) and direct runoff (Q) in x-y coordinates

(1)

Table 1.

Runoff velocity and travel distance per hour by precipitation

Fig. 3.

Watershed with dotted isochrome lines and travel area (Ai) per hour in x-y coordinates in case of 10 mm precipitation

(2)

Table 2.

Calculation of runoff and unit hydrograph of 10 mm precipitation

Fig. 4.

Same as Fig. 3 in case of 40 mm precipitation

Table 3.

Calculation of runoff and unit hydrograph of 40 mm precipitation

Fig. 5.

Same as Fig. 3 in case of 90 mm precipitation

Table 4.

Calculation of runoff and unit hydrograph of 90 mm precipitation

Fig. 6.

Same as Fig. 3 in case of 160 mm precipitation

Table 5.

Calculation of runoff and unit hydrograph of 160 mm precipitation

Fig. 7.

Same as Fig. 3 in case of 250 mm precipitation

Table 6.

Calculation of runoff and unit hydrograph of 250 mm precipitation

Fig. 8.

Same as Fig. 3 in case of 360 mm precipitation

Table 7.

Calculation of runoff and unit hydrograph of 360 mm precipitation

Fig. 9.

Same as Fig. 3 in case of 640 mm precipitation

Table 8.

Calculation of runoff and unit hydrograph of 640 mm precipitation

Fig. 10.

Same as Fig. 3 in case of 1,000 mm precipitation

Table 9.

Calculation of runoff and unit hydrograph of 1,000 mm precipitation

Fig. 11.

Same as Fig. 3 in case of 1,210 mm precipitation

Table 10.

Calculation of runoff and unit hydrograph of 1,210 mm precipitation

Fig. 12.

Same as Fig. 3 in case of 1,690 mm precipitation

Table 11.

Calculation of runoff and unit hydrograph of 1,690 mm precipitation

Fig. 13.

Unit hydrographs calculated for 40 mm, 90 mm, 160 mm, 250 mm, 360 mm, 640 mm, 1,000 mm, 1,210 mm and 1,690 mm precipitation

Table 12.

Peak flow and time to peak of unit hydrograph by precipitation

(3)

Fig. 14.

Relationship between precipitation scale and peak flow of unit hydograph

Fig. 15.

Relationship between precipitation scale and time to peak of unit hydrograph

(4)

(5)

(6)

(7)

Fig. 16.

Seolmacheon watershed, Paju, Kyeonggi, South Korea (Yoo, 2010; area size = 8.5 km2, average slope is about 20%, and it’s mostly forested)

Fig. 17.

Edwardsville watershed, Illinois, US (Minshall, 1960; area size = 0.110 km2, two-thirds of area slope is less than 1%, and it’s mostly cultivated and in legume hay)

(8)

Table 13.

Comparison of the results of previous studies and this study

Fig. 18.

Relationship between Qm (Average Discharge) in mm/hr and TL (Lag Time) in hour to compare this result with previous studies (Minshall, 1960; Yoo, 2010)

Acknowledgements

Conflicts of Interest

References

Schematic of watershed applied for effective precipitation (P_e) and direct runoff (Q) in x-y coordinates

Watershed with dotted isochrome lines and travel area ( $A_{i}$ ) per hour in x-y coordinates in case of 10 mm precipitation

Seolmacheon watershed, Paju, Kyeonggi, South Korea (Yoo, 2010; area size = 8.5 km², average slope is about 20%, and it’s mostly forested)

Edwardsville watershed, Illinois, US (Minshall, 1960; area size = 0.110 km², two-thirds of area slope is less than 1%, and it’s mostly cultivated and in legume hay)

Relationship between Q_m(Average Discharge) in mm/hr and T_L(Lag Time) in hour to compare this result with previous studies (Minshall, 1960; Yoo, 2010)