Impact of Baekrokdam precipitation observation data on improving groundwater level prediction in mid-mountainous region of Jeju Island

Mun-Ju Shin; Jeong-Hun Kim; Su-Yeon Kang; Soo-Hyoung Moon; Eun Hee Hyun

doi:10.3741/JKWRA.2024.57.10.673

Preview

Research Article

Journal of Korea Water Resources Association. 31 October 2024. 673-686
https://doi.org/10.3741/JKWRA.2024.57.10.673

Impact of Baekrokdam precipitation observation data on improving groundwater level prediction in mid-mountainous region of Jeju Island

백록담 강수량 관측자료가 제주도 중산간지역 지하수위 예측 향상에 미치는 영향

Mun-Ju Shin^a^*

Jeong-Hun Kim^b

Su-Yeon Kang^c

Soo-Hyoung Moon^d

Eun Hee Hyun^e

신 문주^a^*

김 정훈^b

강 수연^c

문 수형^d

현 은희^e

^aSenior Researcher, Drinking Water Research Laboratory, Jeju Special Self-Governing Province Development Corporation, Jeju, Korea

^bResearcher, Drinking Water Research Laboratory, Jeju Special Self-Governing Province Development Corporation, Jeju, Korea

^cResearcher, Drinking Water Research Laboratory, Jeju Special Self-Governing Province Development Corporation, Jeju, Korea

^dChief Researcher, Drinking Water Research Laboratory, Jeju Special Self-Governing Province Development Corporation, Jeju, Korea

^eDirector, R&D Innovation Division, Jeju Special Self-Governing Province Development Corporation, Jeju, Korea

^a제주특별자치도개발공사 먹는물연구소 선임연구원

^b제주특별자치도개발공사 먹는물연구소 연구원

^c제주특별자치도개발공사 먹는물연구소 연구원

^d제주특별자치도개발공사 먹는물연구소 수석연구원

^e제주특별자치도개발공사 R&D혁신본부 본부장

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by/4.0):

©It is identical to the Creative Commons Attribution Non-commercial License (https://creativecommons.org/licenses/by/4.0)

ABSTRACT

Groundwater is an important water resource used for various purposes along with surface water. Jeju Island relies on groundwater for most of its water use, so predicting and managing groundwater volume is very important for sustainable use of groundwater. In this study, precipitation data from the Baekrokdam Climate Change Observatory was additionally used to accurately predict groundwater levels. We compared and analyzed the improvement in monthly groundwater level prediction performance of the ANN and LSTM models for two observation wells located in the mid-mountainous area of the Pyoseon watershed in Jeju Island. As a result, when Baekrokdam precipitation data was not used, the NSE values of the two artificial intelligence models were over 0.871, showing very high groundwater level prediction performance. The LSTM model showed relatively higher prediction performance at high and low groundwater levels than the ANN model. We found that the prediction performance decreases as the variation characteristics of the groundwater level become more complex. When Baekrokdam precipitation data was additionally used, the NSE values of the two artificial intelligence models were above 0.907, indicating improved prediction performance, and the NSE value was improved by up to 0.036. This means that when additional rainfall in the upstream area is used, the artificial intelligence model can more appropriately interpret the fluctuating characteristics of the groundwater level. In addition, the additional use of Baekrokdam precipitation data further helped improve groundwater level prediction for observation well, where groundwater level prediction is relatively difficult, and artificial intelligence models, which have relatively low groundwater level prediction performance. In particular, when Baekrokdam precipitation data was additionally used for a specific observation well, the groundwater level prediction performance of the ANN model was improved to a level comparable to that of the LSTM model. The methods and results of this study can be useful in future research using artificial intelligence models.

Keywords

Baekrokdam precipitation

LSTM

ANN

Groundwater level prediction

Improvement of prediction performance

지하수는 지표수와 함께 다양한 용수로 사용되는 중요한 수자원이며, 특히 제주도의 경우 대부분의 용수를 지하수에 의존하고 있기 때문에 지속가능한 지하수의 이용을 위해 지하수량의 예측 및 관리는 매우 중요하다. 본 연구에서는 정확한 지하수위 예측을 위해 백록담 기후변화관측소의 강수량 데이터를 추가적으로 사용하여 제주도 표선유역 중산간 지역에 위치한 2개 관측정에 대해 ANN 모델과 LSTM 모델의 월 단위 지하수위 예측성능 개선효과를 비교분석 하였다. 그 결과, 백록담 강수량 데이터를 사용하지 않은 경우 두 인공지능 모델의 NSE 값은 0.871 이상을 보여 높은 지하수위 예측성능을 보였다. LSTM 모델은 ANN 모델보다 고수위 및 저수위에서 상대적으로 높은 예측성능을 나타내었으며, 관측지하수위의 변동폭이 커 변동특성이 복잡할수록 예측성능이 낮아짐을 확인하였다. 백록담 강수량 데이터를 추가적으로 사용한 경우 두 인공지능 모델의 NSE 값은 0.907 이상을 보여 개선된 예측성능을 나타내었으며, NSE 값은 최대 0.036만큼 개선되었다. 이것은 상류지역의 강수량을 추가적으로 사용 시 지하수위 해석에 도움이 되는 정보가 많아져 인공지능 모델은 지하수위의 변동특성을 더욱 적절히 해석할 수 있다는 것을 의미한다. 또한 관측지하수위 변동폭이 더 커 지하수위 예측이 상대적으로 어려운 관측정일수록 그리고 지하수위 예측성능이 상대적으로 낮은 인공지능 모델일수록 백록담 강수량 데이터의 추가사용 시 지하수위 예측 개선에 더욱 도움이 되었다. 특히, 특정 관측정에 대해 백록담 강수량 데이터를 추가적으로 사용 시 ANN 모델의 지하수위 예측성능은 LSTM 모델과 대등한 수준으로 개선되었다. 본 연구의 방법 및 결과는 향후 인공지능 모델을 활용한 연구에서 유용하게 사용될 수 있다.

키워드

백록담 강수량

LSTM

ANN

지하수위 예측

예측성능 개선

MAIN

1. 서 론
2. 자료 및 방법
2.1 연구대상 지역 및 자료
2.2 인공지능 모델
2.3 연구방법
3. 결과 및 고찰
3.1 백록담 강수량 데이터 제외 시 인공지능 모델의 지하수위 예측성능 분석
3.2 백록담 강수량 데이터 포함 시 인공지능 모델의 지하수위 예측성능 분석
3.3 백록담 강수량 추가 사용 시 인공지능 모델의 지하수위 예측성능 개선효과 분석
4. 결 론

1. 서 론

지하수는 지표수와 더불어 내륙과 섬 지역에서 농업, 공업 및 생활 등에 필요한 다양한 용수로 사용할 수 있는 중요한 수자원이다. 지하수가 전체 수자원의 82%를 차지하는(JSSGP, 2022) 제주도의 경우 지속가능한 지하수의 이용을 위해 지하수량의 예측 및 관리는 매우 중요한 사항이다. 특히, 최근 기후변화 및 기상변화에 따른 강수량의 변화는 지하수량의 변화에 직접적인 영향을 미치기 때문에 가능한 다수의 그리고 유용한 기상관측소의 데이터를 사용하여 정확한 미래 지하수위 변동성을 예측할 수 있는 연구가 반드시 필요하다.

지하수위 변동성을 모의하기 위해 물리적 기반 개념모델 및 수치모델을 사용할 수 있다(Mohanty et al., 2013; Bizhanimanzar et al., 2019). MODFLOW (McDonald and Harbaugh, 1988) 등 지하수 수치모델은 연구 및 실무에 널리 사용되고 있다. 지하수 수치모델을 활용한 모의결과의 정밀도와 정확성은 대수층의 특성, 지하의 지질 및 지형 등과 관련된 수문지질학적 데이터의 품질과 시공간적 데이터의 양에 영향을 받으므로 데이터의 취득이 제한된 지역의 경우 모델링 및 결과의 신뢰성은 제한된다(Adamowski and Chan, 2011; Barthel and Banzhaf, 2016; Sun et al., 2016; Tao et al., 2022).

수문지질학에 대한 물리적 데이터가 제한되어 있고 수문 프로세스의 물리적 이해보다 정확한 지하수위 예측결과를 도출하는 것이 목적인 경우에는 블랙박스 모델인 인공지능 모델이 수치모델보다 적합하다(Adamowski and Chan, 2011). 인공지능 모델은 지난 20여년 동안 수문지질학적 데이터 취득 제한 등 기존 수치모델의 단점을 극복하고 지하수위 모의를 위해 널리 그리고 성공적으로 사용되었으며 그 유용성을 많은 연구에서 보고하였다(Rajaee et al., 2019; Tao et al., 2022). 인공신경망 모델(Artificial Neural Network, ANN)(Lallahem et al., 2005), 퍼지 기반 모델(Adaptive Neuro Fuzzy Inference System)(Jeihouni et al., 2019), 지원 벡터 머신(Support Vector Machine)(Gong et al., 2016), 트리 기반 모델(Random Forest) (Davoudi Moghaddam et al., 2020), 유전자 프로그래밍(Genetic Programming)(Fallah-Mehdipour et al., 2013), 극단 학습 머신(Extreme Learning Machine)(Alizamir et al., 2018) 등이 지하수위 모의를 위해 사용되었다. 최근에는 딥러닝 순환신경망 모델인 장단기기억 모델(Long Short-Term Memory, LSTM)(Kow et al., 2024)과 게이트 순환 유닛(Gated Recurrent Unit)(Gharehbaghi et al., 2022) 등의 인공지능 모델이 지하수위 모의를 위해 사용되었으며 그 사용 빈도가 크게 늘고 있다. 특히, ANN 모델과 LSTM 모델은 다양한 수문학 및 수자원분야 연구에 사용된 빈도가 높다(Sit et al., 2020).

제주도의 중산간 지역은 화산활동에 의해 형성된 복잡한 지하지질로 인해 인근 지역의 관측정이라 하더라도 지하수위 변동특성이 매우 다르고 복잡하다. 또한 지표면부터 대수층까지 화산지층의 두께는 매우 커 지하수 흐름특성을 파악하기 어려우며 한라산 국립공원 내 지하지질에 대한 데이터는 충분하지 않다. 섬 지역에 대해 인공지능 모델을 활용한 지하수위 모의 연구가 있었지만(Mohanty et al., 2010; Payne et al., 2022; Kim et al., 2023) 섬 지역의 정확한 지하수위 예측을 위해 추가적인 데이터 활용 등에 대한 연구는 충분하지 않다.

본 연구의 목적은 제주도 내 표선유역 중산간지역에 위치한 서로 다른 지하수위 변동특성을 보이는 2개 관측정의 정확한 월 단위 지하수위 예측을 위해 상류지역에 위치한 백록담 기후변화관측소의 강수량 데이터를 추가적으로 사용하여 인공지능 모델의 지하수위 예측성능 개선효과를 비교분석 하는 것에 있다. 지하수위 예측을 위해 수문학 및 수자원분야 연구에 사용빈도가 높은 인공신경망(ANN) 모델과 장단기기억(LSTM) 모델을 사용하였다. 기존 연구와의 차이점으로 본 연구에서는 연구용으로만 제공되고 있는 희귀자료인 백록담 강수량 데이터를 추가적으로 사용 시 인공지능 모델이 제주도의 화산활동에 따른 복잡한 지하지질 특성에 의해 예측이 상대적으로 어려운 관측 지하수위를 더욱 적절히 모사하는지 비교분석 한다는 점에 있다. 본 연구의 연구방법은 2절에서 확인할 수 있으며 연구결과와 결론은 각각 3절과 4절에 기술하였다.

2. 자료 및 방법

2.1 연구대상 지역 및 자료

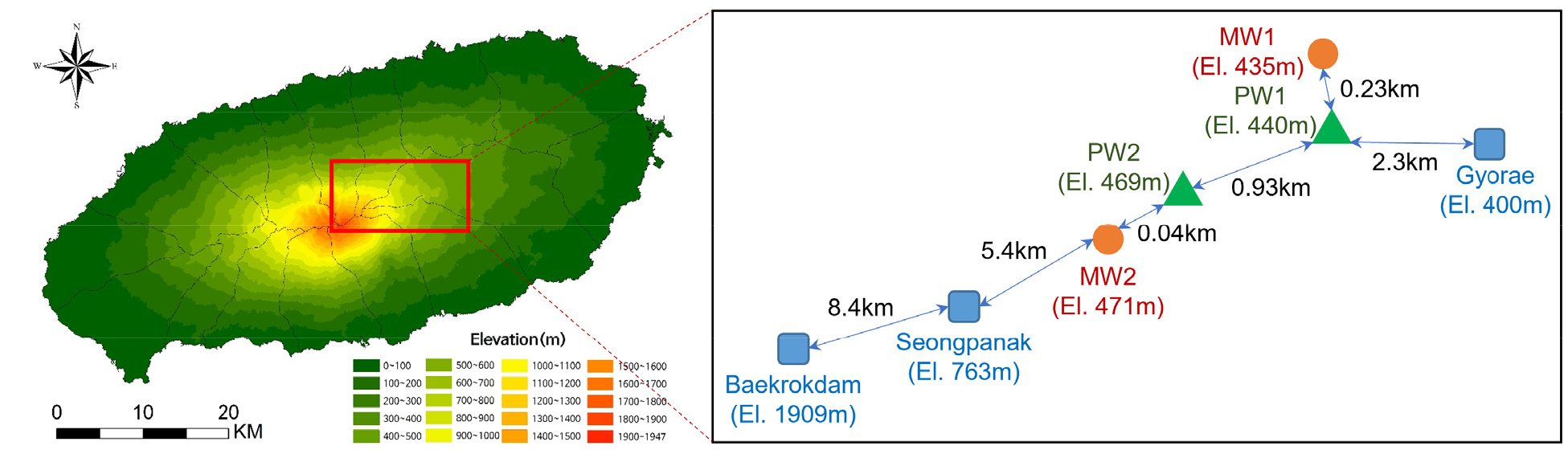
연구대상지역은 한국의 제주도 남동쪽 표선유역의 중산간에 위치한 2개 지하수위 관측정 지점이다(Fig. 1). 본 연구에 사용된 데이터는 백록담 기후변화관측소 분단위 강수량 데이터, 연구대상지역 인근의 2개 강우관측소(성판악, 교래) 일단위 강수량 데이터, 2개 지하수위 관측정 일단위 지하수위 데이터와 2개 지하수 취수원 일단위 취수량 데이터이다(Table 1). 이 분단위 및 일단위 데이터는 인공지능 모델을 이용한 월단위 지하수위 모의를 위해 월단위 데이터로 변환하였다. 백록담 기후변화관측소는 제주지방기상청에서 운영하는 국내 최정상 자동기상관측소(Automatic Weather Station)이다. 이 관측소에서 수집되는 기상 데이터는 연구목적을 위한 사용에 한해 제공되며 공개적으로 제공되지 않는 자료이다. 본 연구에서는 제주지방기상청에서 백록담 기상 데이터를 연구목적으로 제공받아 사용하였다. 성판악 강우관측소는 기상청(http:// www.weather.go.kr/)에서 운영하는 자동기상관측소이며, 교래 강우관측소는 제주도 재난안전대책본부(http://bangjae.jeju119.go.kr/)에서 운영하고 있다. 이 두 강우관측소의 데이터는 웹사이트에서 다운받아 사용할 수 있다. 지하수위 및 취수량 데이터는 제주특별자치도개발공사에서 실시간으로 관측 및 관리하고 있으며 공개적으로 제공되지 않는 자료이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F1.jpg

Fig. 1.

Schematic diagram of the locations of precipitation observation stations, groundwater withdrawal wells, and groundwater level monitoring wells

Table 1.

Period of precipitation, groundwater withdrawal and groundwater level data

Classification	Station name	Data period	Remarks
Rainfall station	Baekrokdam	2015. 12. 01. ~ 2022. 12. 31.	Precipitation (mm/min)
	Seongpanak	1992. 01. 01. ~ 2022. 12. 31.	Precipitation (mm/day)
	Gyorae	1992. 01. 01. ~ 2022. 12. 31.	Precipitation (mm/day)
Pumping well	PW1	2001. 01. 01. ~ 2022. 12. 31.	Pumping rate (㎥/day)
Pumping well	PW2	2013. 07. 31. ~ 2022. 12. 31.	Pumping rate (㎥/day)
Monitoring well	MW1	2015. 05. 13. ~ 2022. 12. 31.	Groundwater level (m)
Monitoring well	MW2	2012. 03. 13. ~ 2022. 12. 31.	Groundwater level (m)

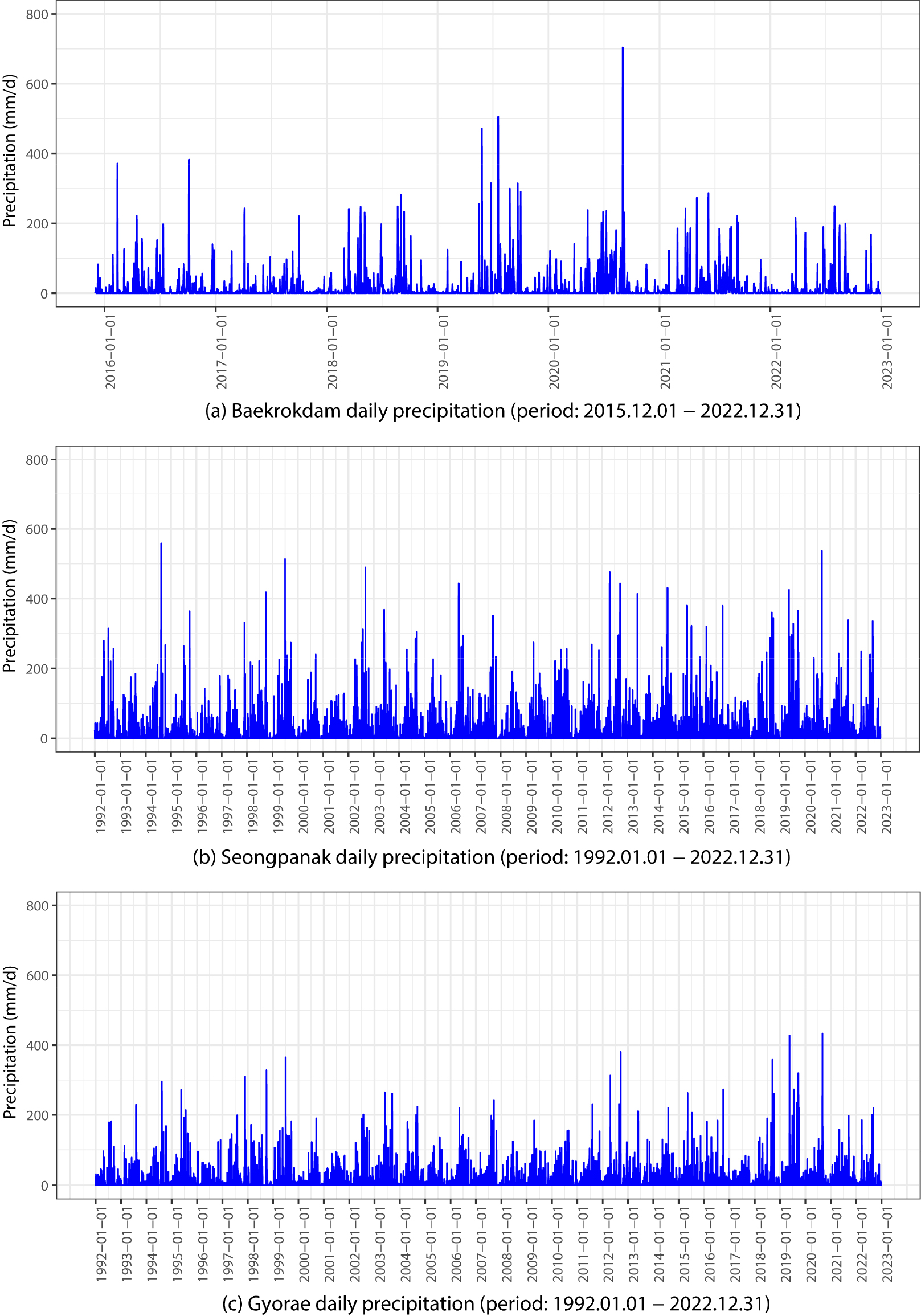
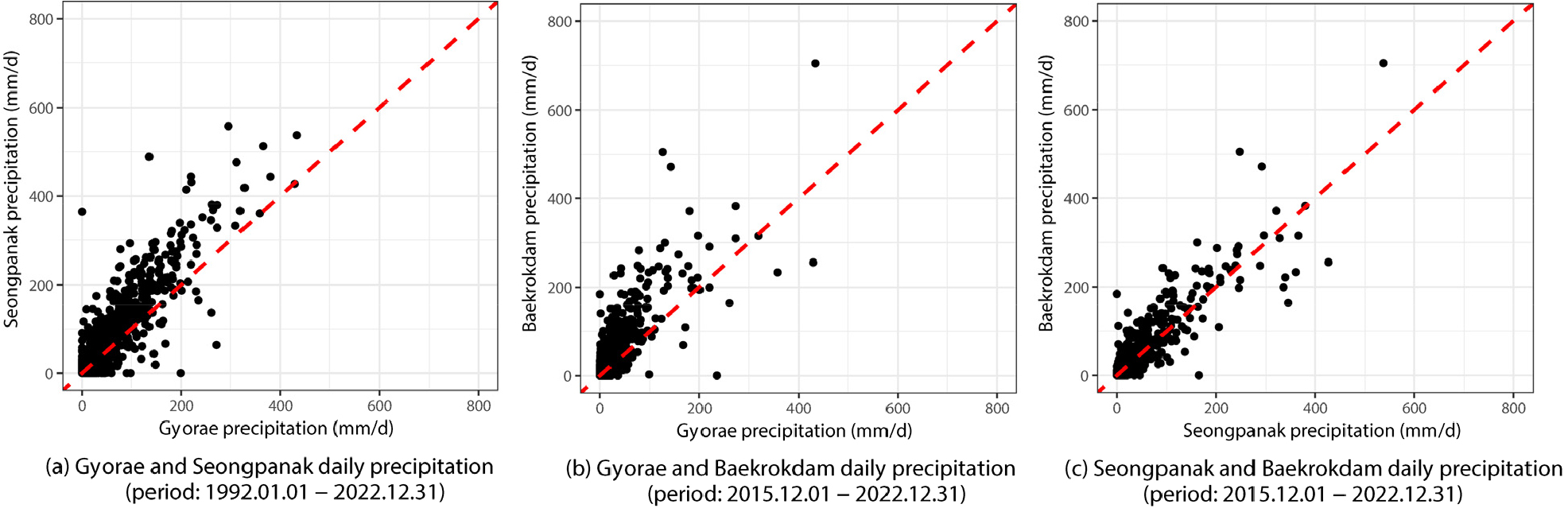
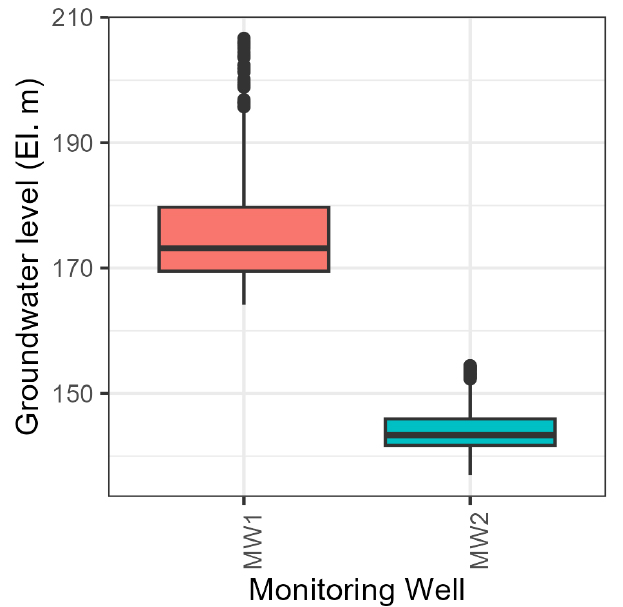
백록담, 성판악과 교래 강우관측소의 일단위 강수량은 전반적으로 백록담, 성판악, 교래 순으로 많은 것을 확인할 수 있다(Figs. 2 and 3). Fig. 1에서 도시한 바와 같이 각 관측소의 고도는 백록담 관측소(El. 1,909 m), 성판악 관측소(El. 763 m), 교래 관측소(El. 400 m) 순으로 높으며, 산지효과로 인해 고도가 높은 강우관측소일수록 더 많은 강수량을 나타내는 것으로 판단된다. 관측정1(MW1)의 일단위 지하수위 최대 변동폭(42.5 m)은 관측정2(MW2)의 일단위 지하수위 최대 변동폭(17.5 m)보다 25 m가 크다(Fig. 4). 관측정1과 관측정2는 직선거리로 약 1.2 km 이격되어 있다. 그리고 관측정1의 표고는 관측정2의 표고보다 낮으나(Fig. 1) 관측정1의 지하수위는 관측정2의 지하수위보다 높게 형성되어 있다(Fig. 4). 이러한 현상은 제주도의 수차례 화산활동으로 인해 형성된 복잡한 지하지질이 관정별 수리지질학적 특성에 영향을 미친 것으로 판단된다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F2.jpg

Fig. 2.

Precipitation time series data from Baekrokdam, Seongpanak, and Gyorae precipitation observation stations

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F3.jpg

Fig. 3.

Comparison of precipitation at Baekrokdam, Seongpanak, and Gyorae precipitation observation stations

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F4.jpg

Fig. 4.

Groundwater level fluctuation range of groundwater level monitoring wells

2.2 인공지능 모델

2.2.1 인공신경망 모델

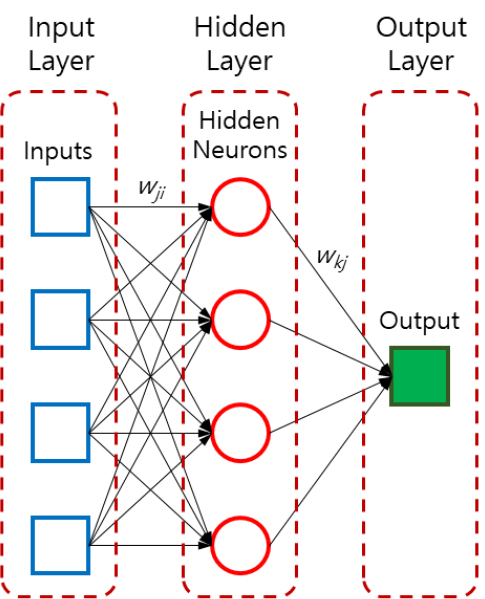
인공신경망(ANN) 모델은 수많은 뉴런과 시냅스의 결합을 통해 반응을 전달하는 인간의 뇌 구조를 모방하여 복잡한 비선형적인 문제들을 병렬적 학습을 통해 효율적으로 자연현상을 모사하는 기계학습 방법 중 하나이다(Haykin, 2009). 순전파(feed-forward) 모델인 ANN 모델은 대표적인 기계학습법으로써 지하수 분야에 널리 사용되어 왔다(Mirarabi et al., 2019; Seifi et al., 2020; Yin et al., 2021; Kim and Lee, 2022; Seidu et al., 2023). 이 모델은 목표변수와 관련된 복수의 입력변수들을 수많은 뉴런(노드)로 연결된 네트워크를 사용하여 비선형적인 현상을 모사한다(Adamowski and Chan, 2011). ANN 모델은 연구 지역에 대해 물리적 모델에 필요한 물리적 특성자료가 모의에 필요없다는 장점이 있으며, 목표 관측 시계열 데이터의 모사를 위해 복수의 입력 관측 시계열 데이터와 목표 관측 시계열 데이터 간의 상관관계를 이용한다(Jha and Sahoo, 2014). 이 모델은 입력층(input layer), 단수 또는 복수의 은닉층(hidden layer), 마지막으로 출력층(output layer)으로 구성된다(Fig. 5). 각 층은 단수 또는 복수의 뉴런으로 구성되며, 입력층의 입력변수 값에 매개변수 값인 가중치를 곱하고 편이(bias)를 더한 값에 활성화함수를 곱한 값을 다음 층에 전달한다. 이 과정은 출력층까지 순차적으로 수행하며, 이러한 순전파(feed-forward) 계산 과정을 통해 목표 관측 시계열 데이터를 모사하는 최종 출력값을 계산한다. ANN 모델의 계산과정은 다음식으로 표현할 수 있다(Kim and Valdés, 2003).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F5.jpg

Fig. 5.

The structure of ANN model (Shin et al., 2021)

(1)

\hat{y_{k}} = f_{o} [\sum_{j = 1}^{m} w_{k j} . f_{h} (\sum_{i = 1}^{n} w_{j i} x_{i} + w_{j o}) + w_{k o}]

여기에서 $w_{j i}$ 는 입력층의 $i$ 번째 뉴런에서 은닉층의 $j$ 번째 뉴런으로의 연결강도(가중치), $x_{i}$ 는 입력층의 $i$ 번째 입력변수, $w_{j o}$ 는 $j$ 번째 은닉뉴런의 편이, $f_{h}$ 는 은닉뉴런의 활성화함수, $w_{k j}$ 는 은닉층의 $j$ 번째 뉴런에서 출력층의 $k$ 번째 뉴런으로의 연결강도, $w_{k o}$ 는 $k$ 번째 출력뉴런의 편이, $f_{o}$ 는 출력뉴런의 활성화함수, $\hat{y_{k}}$ 는 출력변수로써 모의결과를 나타낸다. 이 가중치들은 역전파(backpropagation) 알고리즘(Rumelhart et al., 1986)을 통해 ANN 모델의 모의 시계열 결과와 관측 시계열 데이터 간의 오차가 최소화(학습)되도록 최적의 값으로 업데이트된다(Haykin, 2009). 뉴런의 편이는 가중된 입력신호의 합을 증가 또는 감소시키는 역할을 하며, 회귀모델에서 절편의 역할을 한다(Haykin, 2009; Sahoo et al., 2017). 은닉뉴련의 활성화함수는 최근 인공지능 연구에 널리 사용되는 Rectified Linear Unit (ReLU)(Hahnloser et al., 2000)를 사용하였다.

2.2.2 장단기기억 모델

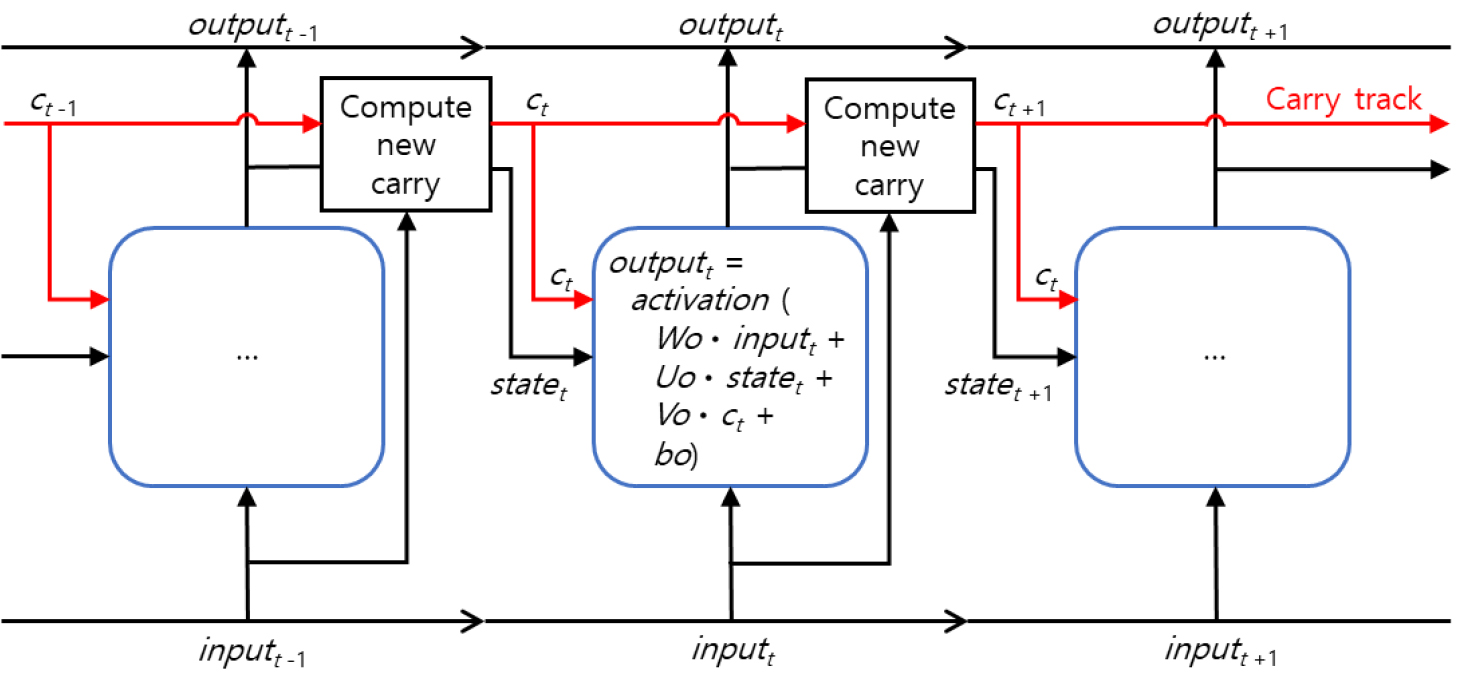
장단기기억(LSTM)(Hochreiter and Schmidhuber, 1997) 모델은 인공지능 모델의 학습 시 데이터 정보의 장기간 기억을 위한 능력(long-term dependencies)을 저해하는 경사소멸(vanishing gradients) 문제(Bengio et al., 1994)를 해결하기 위해 개발된 순환신경망 모델의 일종이다. LSTM 모델은 최근 지하수 및 지표수 예측 등 다양한 분야에 널리 적용되고 있는 딥러닝 인공지능 모델이다(Shin et al., 2020; Müller et al., 2021; Sun et al., 2022; Gholizadeh et al., 2023; Kow et al., 2024). LSTM 모델은 carry track이라는 일종의 컨베이어벨트를 사용하여 시계열 데이터 내 각 계산시간(time step, t)에서 추출한 정보를 장기간 기억한다(Fig. 6). 시계열 데이터의 시간대별 처리 과정과 평행하게 배치한 carry track을 통해 데이터에서 추출한 정보를 이동시키고 각 계산 시간대에서 추출한 정보를 필요할 때마다 재사용한다. 따라서 LSTM 모델은 carry track의 사용을 통해 시계열 데이터의 계산 시 오래된 정보가 사라지는 문제를 해결한다(Chollet and Allaire, 2018). 이 모델은 아래의 네 가지 변환을 사용하여 데이터 내 장기간의 정보를 학습한다. 각 뉴런에서 t 시간대의 결과( $o u t p u t_{t}$ )는 아래와 같이 계산된다.

(2)

o u t p u t_{t} = a c t i v a t i o n (W o \cdot i n p u t_{t} + U o \cdot s t a t e_{t} + V o \cdot c_{t} + b o)

여기에서 $i n p u t_{t}$ 는 t 시간대의 입력 데이터, $s t a t e_{t}$ 는 t 시간대의 상태로써 t-1 시간대의 결과의 상태, $c_{t}$ 는 t 시간대의 carry 값이다. $W o$ , $U o$ 그리고 $V o$ 는 결과계산을 위한 $i n p u t_{t}$ , $s t a t e_{t}$ , $c_{t}$ 각각의 가중치 행렬이며 •은 내적(dot product)을 의미한다. 가중치는 LSTM의 매개변수이고 $b o$ 는 뉴런의 편이이며 $a c t i v a t i o n$ 은 sigmoid 함수와 tanh 함수를 사용하는 활성화함수이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F6.jpg

Fig. 6.

The structure of LSTM model (Shin et al., 2020)

carry 값은 아래의 세 가지 개별적인 변환을 통해 업데이트된다.

(3)

i_{t} = s i g m o i d (W i ∙ i n p u t_{t} + U i ∙ s t a t e_{t} + b i)

(4)

f_{t} = s i g m o i d (W f ∙ i n p u t_{t} + U f ∙ s t a t e_{t} + b f)

(5)

k_{t} = t a n h (W k ∙ i n p u t_{t} + U k ∙ s t a t e_{t} + b k)

(6)

c_{t + 1} = i_{t} k_{t} + c_{t} f_{t}

여기에서 $i_{t}$ 는 sigmoid 함수([0, 1]의 범위)를 통해 새롭게 추가된 정보, $f_{t}$ 는 sigmoid 함수를 통해 삭제된 정보, $k_{t}$ 는 $t a n h$ 함수([-1, 1]의 범위)를 통한 정보의 중요도를 의미한다. 즉, $i_{t}$ 와 $k_{t}$ 의 곱셈 과정을 통해 새로운 정보를 얻고, $c_{t}$ 와 $f_{t}$ 의 곱셈 과정을 통해 관련성 없는 carry 내 정보를 제거하며, $i_{t} k_{t}$ 와 $c_{t} f_{t}$ 의 덧셈 과정을 통해 새로운 carry 값을 얻는다. 따라서 LSTM 모델은 carry track 기능을 사용하여 다음 번 출력과 다음 번 상태를 변조하는 특징이 있다(Chollet and Allaire, 2018). 본 연구에서는 R 언어 기반 딥러닝 프레임워크인 Keras 패키지(Falbel et al., 2019)에서 제공하는 ANN 및 LSTM 모델을 사용하였다.

2.3 연구방법

ANN 모델과 LSTM 모델에 백록담 강수량 데이터의 사용 여부가 지하수위 변동특성이 서로 다른 2개 지하수위 관측정의 1개월 후 지하수위 예측개선에 미치는 영향을 분석하였다. 또한 ANN 모델과 LSTM 모델 간의 지하수위 예측성능을 지하수위 관측정별로 비교 및 분석하였다. 1개월 후 지하수위를 예측한 이유는 월단위 지하수위 예측의 경우 ANN 모델 및 LSTM 모델의 1개 스텝(time step)에 대한 미래 예측성능이 가장 좋음에 따라 각 인공지능 모델의 지하수위 예측 특성을 적절히 반영할 수 있기 때문이다.

인공지능 모델의 학습, 검증 및 테스트 기간은 다음과 같이 서로 독립된 기간을 사용하였다. 백록담 강수량 데이터의 기간이 나머지 데이터의 기간보다 짧으나 인공지능 모델에 사용되는 데이터의 기간은 모든 입력자료가 동일해야 하므로 학습기간은 2016년 1월부터 2020년 12월까지, 검증기간은 2021년 1월부터 2022년 6월까지, 테스트기간은 2022년 7월부터 2022년 12월까지로 설정하였다. 사용된 월단위 강수량, 취수량, 지하수위 데이터의 샘플수는 학습기간의 경우 420개(60개월×7개 관측소), 검증기간의 경우 126개(18개월×7개 관측소), 테스트기간의 경우 42개(6개월×7개 관측소)로 총 588개이다. 사용된 데이터의 총 기간이 7년으로 짧아 충분한 학습을 위해 대부분의 데이터를 학습 및 검증에 사용하였다. 이에 따라 테스트 기간은 상대적으로 짧아 분석에 사용되는 데이터의 개수가 적어 테스트 기간의 모의성능 통계값을 분석 시 정확한 인공지능 모의성능에 대한 판단이 어려울 수 있다. 또한 전체적인 지하수위 모의성능 개선효과를 분석하는 것이 목적이므로 본 연구에서는 7년간의 전체 모의결과를 사용하여 모의성능 통계값을 도출하였다.

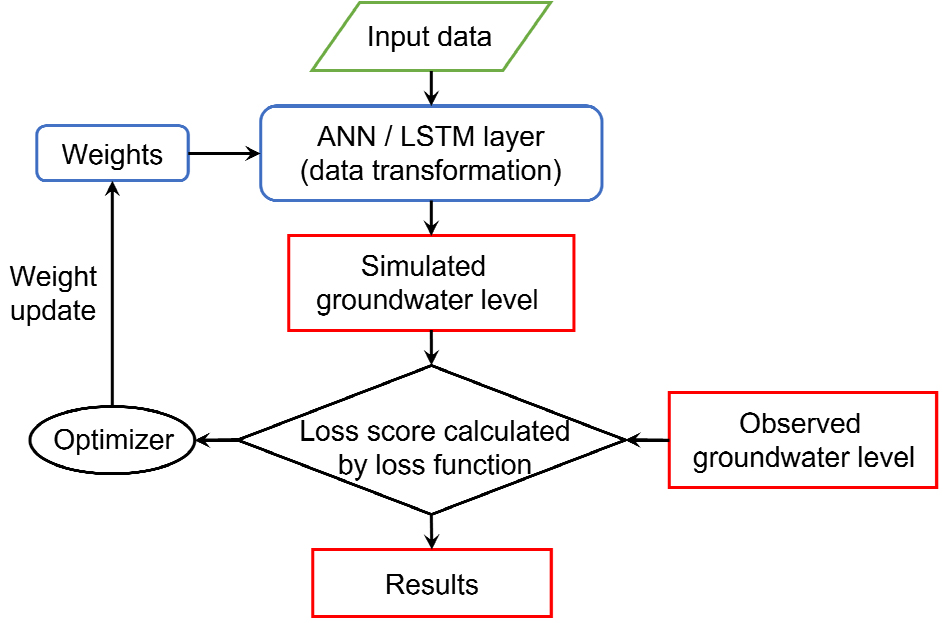
두 인공지능 모델의 학습절차는 다음과 같다(Fig. 7). 인공지능 모델은 매개변수값인 가중치와 활성화함수를 사용하여 입력 시계열 데이터를 모의지하수위 시계열 데이터로 변환한다. 그리고 계산된 모의지하수위 시계열 데이터와 관측지하수위 시계열 데이터를 비교하여 목적함수(loss function)를 계산한다. 본 연구에서는 목적함수로 평균절대오차(mean absolute error)를 적용하였다. 만약 모의지하수위와 관측지하수위 간의 차이가 커 목적함수의 값이 크게 되면 역전파 알고리즘을 이용하는 최적화기(optimizer)를 통해 두 시계열 데이터가 서로 가장 근사하여 목적함수의 값이 최소가 될 때까지 가중치를 업데이트한다. 인공지능 모델의 학습(매개변수 보정) 시 학습기간에 대한 모의결과의 과적합(overfitting)을 방지하기 위해 콜백(callback) 기능을 사용하여 매개변수 보정과정 중에 추정된 매개변수를 검증기간에 대해 검증하였다. 또한 드롭아웃(dropout) 기능을 사용하여 인공지능 모델의 과적합을 방지하였다. 콜백 기능이란 학습 및 검증 기간의 모의결과가 모두 적절히 도출되도록 하기 위해 임의로 설정한 반복횟수(patience)만큼 학습기간에 대해 매개변수를 업데이트 하여도 검증기간의 모의결과가 더 이상 개선되지 않을 때 학습을 조기종료(early-stopping)(Prechelt, 2012) 함으로써 인공지능 모델의 과적합을 방지하는 기능이다. 드롭아웃 기능이란 학습 시 은닉뉴런을 임의로 설정한 비율로 무작위로 비활성화시켜 과적합 문제를 해결하는 기능이다.

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F7.jpg

Fig. 7.

Groundwater level learning procedure of artificial intelligence models (Shin et al., 2021)

인공지능 모델의 적절한 학습을 위해서는 하이퍼매개변수(hyper-parameter)라는 가중치 이외의 매개변수 값의 설정이 중요하다. Chollet and Allaire (2018)에 의하면 하이퍼매개변수 값에 대한 명확한 설정방법과 기준은 없다. 본 연구에서는 시행착오 방법을 사용하여 하이퍼매개변수 값을 설정하였다(Table 2). 각 인공지능 모델은 2개의 은닉층을 사용하였으며, 각 은닉층의 은닉뉴런의 개수(n_units)는 충분한 학습을 위해 100개로 설정하였다. 은닉뉴런이 많을수록 복잡한 데이터의 특성을 더욱 충분히 학습할 수 있고 목적함수 값에 수렴하는 속도가 더욱 빨라진다는 장점이 있다. 하지만 계산시간이 길어지고 학습기간에 대한 과적합 문제가 발생할 수 있는 단점이 있다. 이러한 과적합 문제를 해결하기 위해 드롭아웃 기능과 콜백 기능을 사용하였다. 드롭아웃과 재귀적 드롭아웃(recurrent_dropout)은 각각 0.5로 설정하였으며 콜백 기능의 반복횟수(patience)는 10으로 설정하였다. 인공지능 모델의 효율적인 학습을 위해 한번에 처리할 수 있는 소규모 자료의 개수(batch_size)는 월단위 데이터의 길이를 고려하여 6개로 설정하였다. 인공지능의 최적 가중치를 도출하기 위한 최적화기는 딥러닝 분야에서 널리 사용되고 있는 Adam (Kingma and Ba, 2014)을 적용하였으며 학습률(learning_rate)은 0.001로 설정하였다. 학습 과정 중 데이터 전체에 대해 매개변수를 1번 업데이트 하는 것을 epoch라고 한다. 효율적인 학습을 위해 업데이트 최대 반복 횟수(n_epochs)의 설정이 필요하며 n_epochs 는 50번으로 설정하였다. 각 인공지능 모델의 출력층에 대한 활성화 함수는 Maier and Dandy (2000)의 연구를 참고하여 출력층의 뉴런에 수신되는 입력신호를 그대로 출력신호로 넘기는 선형함수를 사용하였다.

Table 2.

Hyper-parameters of artificial intelligence models

Hyper-Parameter	Range	Setting Value	Description
n_units	-	100	Number of hidden units in hidden layer
batch_size	-	6	Number of samples fed to LSTM in one sub-simulation
dropout	0~1	0.5	Fraction of the units to drop for the linear transformation of the inputs
recurrent_dropout	0~1	0.5	Fraction of the units to drop for the linear transformation of the recurrent state in LSTM
learning_rate	float >= 1	0.001	Learning rate of Adam optimizer
n_epochs	-	50	Number of iterations
patience	-	10	Number of epochs for early termination of training when simulation values do not improve

인공지능 모델의 모의성능을 분석하기 위해 수문학 분야에서 널리 사용되고 있는 평가지수인 Nash-Sutcliffe efficiency (NSE)(Nash and Sutcliffe, 1970), Root Mean Square Error (RMSE)를 사용하였다. NSE는 모의결과의 적절성에 대한 전반적인 정보를 제공하며(Moriasi et al., 2007) RMSE는 모의값과 관측값의 근사 정도를 측정한다(Le et al., 2019). NSE와 RMSE의 식은 아래와 같다.

(7)

N S E = 1 - \frac{\sum_{i = 1}^{n} (Q_{o b s, i} - Q_{s i m, i})^{2}}{\sum_{i = 1}^{n} (Q_{o b s, i} - \bar{Q_{o b s}})^{2}}

(8)

R M S E = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} (Q_{o b s, i} - Q_{s i m, i})^{2}}

여기에서 $n$ 은 시계열자료의 개수, $Q_{o b s, i}$ 와 $Q_{s i m, i}$ 는 각각 $i$ 시간대의 관측 및 모의 지하수위, $\bar{Q_{o b s}}$ 는 관측 지하수위의 평균값이다. NSE는 -∞에서 1의 범위를 가지며 모의값과 관측값이 정확히 일치할 경우 1의 값을 갖고, 모의값이 관측값의 평균값과 동일한 경우 0의 값을 갖는다. RMSE는 관측값과 모의값이 일치할 경우 0의 값을 가진다.

3. 결과 및 고찰

3.1 백록담 강수량 데이터 제외 시 인공지능 모델의 지하수위 예측성능 분석

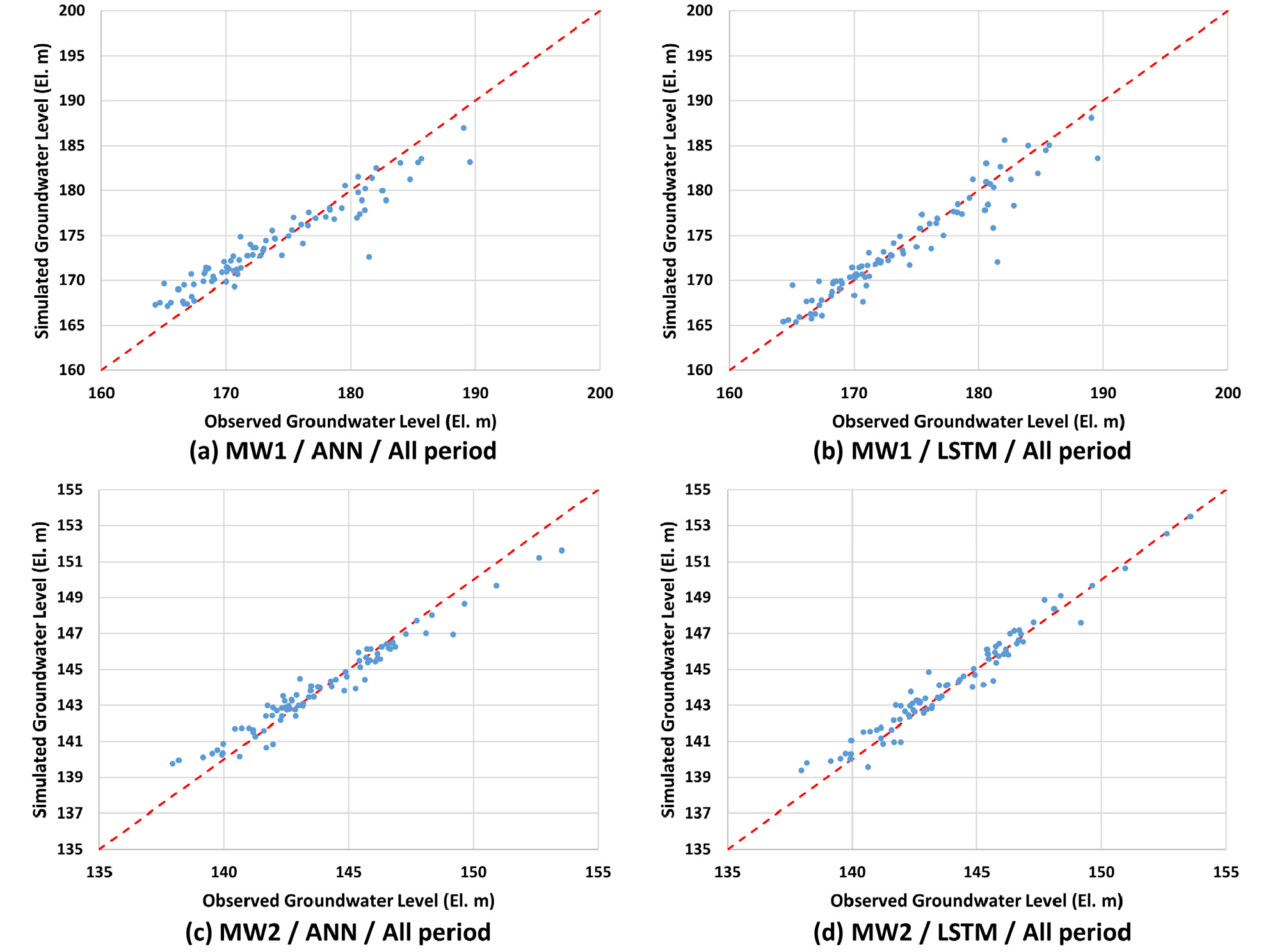
백록담 강수량 데이터를 인공지능 모델의 학습에 사용하지 않은 경우에 대해 2개 관측정 지하수위 1개월 예측결과는 Table 3과 같다. 이 통계값들은 2.3절에서 기술한 바와 같이 학습, 검증 및 테스트 기간을 포함한 전체 모의기간에 대한 결과이다. 지하수위 변동폭이 상대적으로 큰 관측정1(MW1)의 경우 ANN 모델과 LSTM 모델은 NSE 값이 각각 0.871과 0.897로 우수한 모의 성능을 나타내었다(Moriasi et al., 2007). RMSE 값은 ANN 모델의 경우 2.199 m, LSTM 모델의 경우 1.966 m를 나타내어 2 m 내외의 오차를 보이며 관측정1의 큰 월단위 관측지하수위 최대 변동폭(25.2 m)을 고려할 경우 적절한 지하수위 예측능력을 도출하였다고 판단된다. 관련 사례로 Rakhshandehroo et al. (2012)은 이란의 Shiraz 평원을 대상으로 ANN 모델을 사용하여 월단위 지하수위를 예측하였으며, 관측지하수위 최대 변동폭은 14 m이었으며 RMSE는 약 2 m인 결과를 도출하였다. LSTM 모델은 ANN 모델보다 고수위 및 저수위에서 상대적으로 관측값에 근사한 모의결과를 도출하여(Figs. 8(a) and 8(b)) 상대적으로 높은 NSE 값과 상대적으로 낮은 RMSE 값을 나타내었다. 이것은 LSTM 모델이 풍수기와 갈수기의 계절적인 영향을 지하수위 모의에 적절히 반영한다는 것을 의미한다. 정확한 저수위의 모의는 기후변화 등 강수량 변화에 따른 지하수위 하강 예측 및 대응에 있어서 중요한 사항이므로 LSTM 모델의 사용은 제주도 중산간지역 지하수위 예측에 적합하며 비교 기준이 되는 참고 모델로 사용될 수 있다고 판단된다.

Table 3.

Statistics on the one-month groundwater level prediction performance of artificial intelligence models for the entire observation well data period when excluding Baekrokdam precipitation data

Monitoring Well	Performance statistics	ANN	LSTM
MW1	NSE	0.871	0.897
MW1	RMSE	2.199	1.966
MW2	NSE	0.936	0.952
MW2	RMSE	0.761	0.658

지하수위 변동폭이 상대적으로 작은 관측정2(MW2)의 경우 ANN 모델과 LSTM 모델은 NSE 값이 각각 0.936과 0.952로 매우 높은 모의 성능을 나타내었다. RMSE 값은 ANN 모델의 경우 0.761 m, LSTM 모델의 경우 0.658 m를 나타내어 1 m 내의 오차를 보이며 관측정2의 월단위 관측지하수위 최대 변동폭(15.6 m)을 고려할 경우 적합한 지하수위 예측능력을 도출하였다고 판단된다. 관측정1의 경우와 마찬가지로 LSTM 모델은 ANN 모델보다 고수위 및 저수위에서 상대적으로 관측값에 근사한 모의결과를 도출하여(Figs. 8(c) and 8(d)) 상대적으로 높은 NSE 값과 상대적으로 낮은 RMSE 값을 나타내었다. 순전파(feed-forward) 연산방법을 사용하는 ANN 모델은 순환신경망을 사용하는 LSTM 모델보다 구조적으로 단순한 모델의 특성으로 인해 전반적으로 저수위에서 과대추정, 고수위에서 과소추정을 하였으나 중간수위에서 적절한 모의결과를 도출하였다(Fig. 8).

주목할만한 점은 관측지하수위 변동폭이 상대적으로 큰 관측정1에 대한 RMSE 값은 관측지하수위 변동폭이 상대적으로 작은 관측정2에 대한 RMSE 값보다 크다는 점이다. ANN 모델의 경우 관측정1의 RMSE 값인 2.199 m는 관측정2의 RMSE 값인 0.761 m 보다 약 2.9배 컸으며 LSTM 모뎔의 경우는 약 3배(1.966 m/0.658 m)가 컸다. 관측정1의 월단위 관측지하수위 최대 변동폭은 관측정2의 월단위 관측지하수위 최대 변동폭보다 약 1.6배(25.2 m/15.6 m) 컸다. 이것은 비록 관측정 간의 RMSE 값의 차이와 관측지하수위 변동폭의 차이는 동일한 비율로 나타나지 않았지만, 관측지하수위의 변동폭이 크고 지하수위의 변동특성이 복잡할수록 인공지능 모델의 지하수위 예측은 어려워진다는 것을 의미한다. 이러한 현상은 관측정1의 모의결과가 관측정2의 모의결과보다 1:1선(빨간색 대각선)으로부터 더 멀리 분포하는 것을 통해 확인할 수 있다(Figs. 8(a) and 8(c) 및 Figs. 8(b) and 8(d) 비교).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F8.jpg

Fig. 8.

Artificial intelligence models' one-month groundwater level prediction plots for the entire observation well data period when excluding Baekrokdam precipitation data

관측정별 LSTM 모델과 ANN 모델의 NSE 값의 차이는 관측정1의 경우 0.026(0.897-0.871)이었고 관측정2의 경우 0.016(0.952-0.936)을 보여 작은 차이를 나타내었다. 관측정2에 대한 NSE 값의 차이가 관측정1의 경우보다 작은 이유는 관측정2의 지하수위 변동폭이 관측정1의 경우보다 상대적으로 작아 위에서 기술한 바와 같이 관측정2의 지하수위 예측결과가 상대적으로 좋으며 또한 관측정2에 대한 두 인공지능 모델 모두 NSE 값이 0.936 이상의 충분히 높은 지하수위 예측성능을 도출함으로 인해 인공지능 모델 특성의 차이에 의한 예측성능의 차이가 상대적으로 작아진 것이 원인으로 판단된다.

3.2 백록담 강수량 데이터 포함 시 인공지능 모델의 지하수위 예측성능 분석

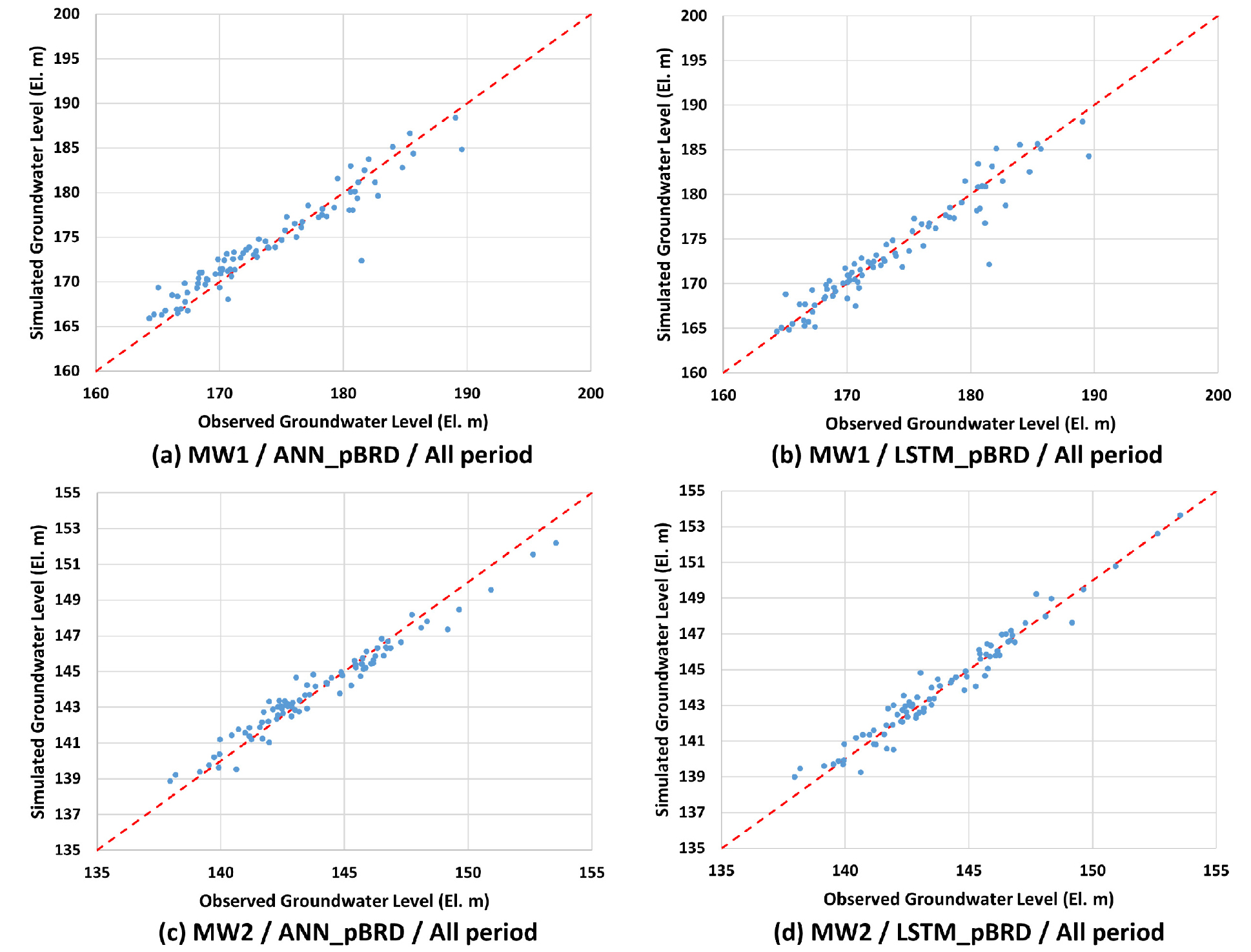
인공지능 모델의 학습에 백록담 강수량 데이터를 추가적으로 사용한 경우에 대해 2개 관측정 지하수위의 1개월 예측결과는 Table 4와 같다. 관측정1의 경우 ANN 모델과 LSTM 모델의 NSE 값은 각각 0.907과 0.908로 도출되어 매우 높은 모의 예측성능을 나타내었으며, 두 모델의 NSE 값의 차이는 단지 0.001를 보여 두 모델의 예측성능은 대등하였다. RMSE 값은 ANN 모델의 경우 1.868 m, LSTM 모델의 경우 1.855 m를 나타내어 2 m 내의 오차를 보여 관측정1의 월단위 관측지하수위 최대 변동폭(25.2 m)을 고려할 경우 적절한 지하수위 예측능력을 도출하였다고 판단된다. LSTM 모델과 ANN 모델은 고수위 및 저수위에서 유사한 모의결과를 도출하였으며 LSTM 모델이 ANN 모델보다 저수위에서 관측지하수위에 약간 더 근사한 모의결과를 보여 저수위 모의에 더욱 적합하였다(Figs. 9(a) and 9(b)).

Table 4.

Statistics on the one-month groundwater level prediction performance of artificial intelligence models for the entire observation well data period when including Baekrokdam precipitation data

Monitoring Well	Performance statistics	ANN_pBRD	LSTM_pBRD
MW1	NSE	0.907	0.908
MW1	RMSE	1.868	1.855
MW2	NSE	0.948	0.956
MW2	RMSE	0.688	0.633

지하수위 변동폭이 상대적으로 작은 관측정2의 경우 ANN 모델과 LSTM 모델은 NSE 값이 각각 0.948과 0.956를 보여 매우 높은 모의 예측성능을 도출하였으며, 두 모델의 NSE 값의 차이는 0.008를 보여 매우 작은 차이를 나타내었다. RMSE 값은 ANN 모델의 경우 0.688 m, LSTM 모델의 경우 0.633 m를 나타내어 1 m 내의 오차를 보이며, 관측정2의 월단위 관측지하수위 최대 변동폭(15.6 m)을 고려할 경우 적절한 지하수위 예측능력을 도출하였다고 판단된다. LSTM 모델은 ANN 모델보다 고수위에서 관측값에 근사한 모의결과를 도출하여(Figs. 9(c) and 9(d)) 상대적으로 높은 NSE 값과 상대적으로 낮은 RMSE 값을 나타내었다. ANN 모델은 고수위에서 과소추정을 하였으나 중간수위와 저수위에서 적절한 모의결과를 도출하였다(Fig. 9(c)).

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F9.jpg

Fig. 9.

Artificial intelligence models' one-month groundwater level prediction plots for the entire observation well data period when including Baekrokdam precipitation data

3.3 백록담 강수량 추가 사용 시 인공지능 모델의 지하수위 예측성능 개선효과 분석

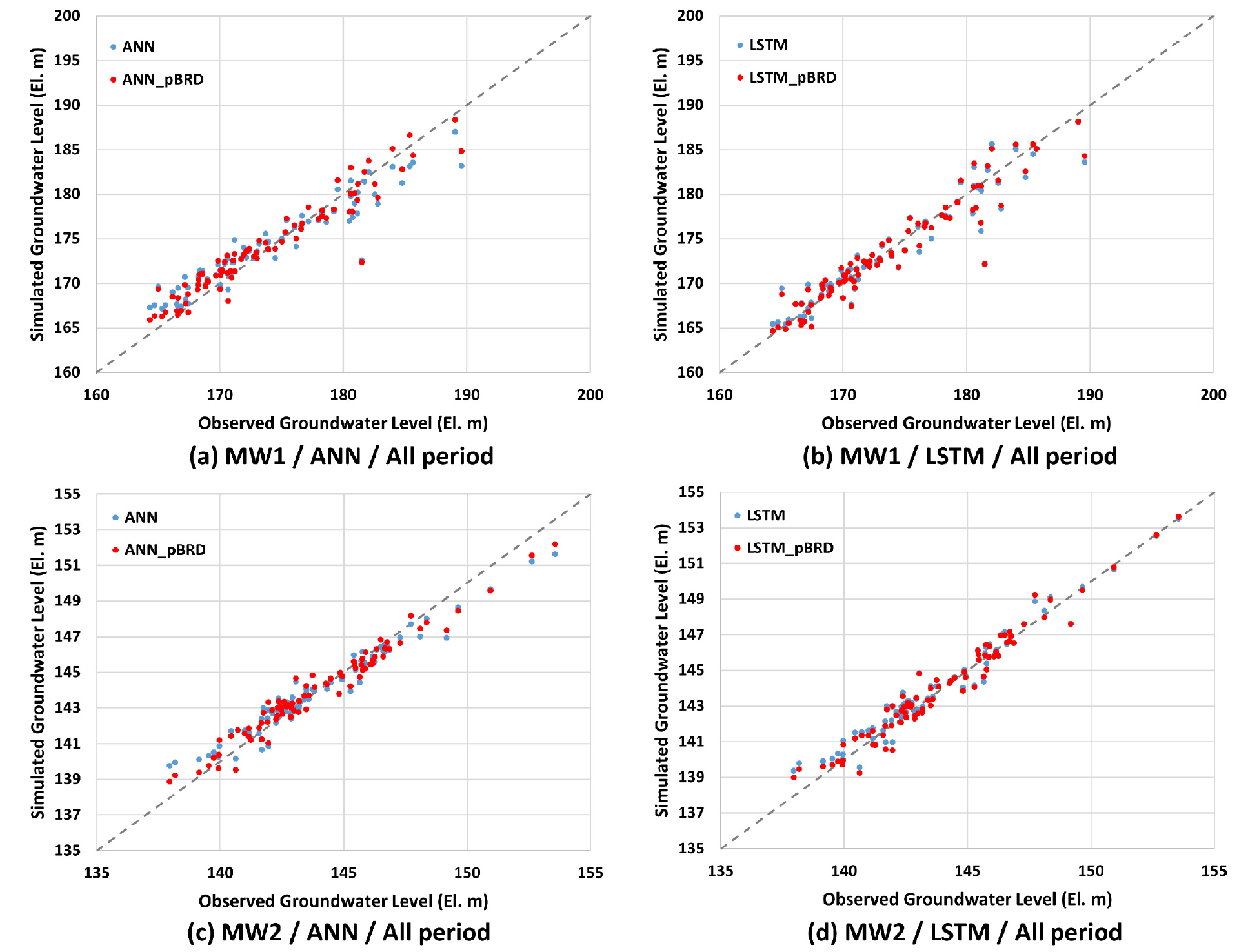
백록담 강수량이 인공지능 모델의 지하수위 예측성능 개선에 미치는 영향은 Table 5와 같다. 관측정1의 경우 백록담 강수량 데이터를 추가적으로 사용 시 ANN 모델과 LSTM 모델은 NSE 값이 각각 0.036와 0.011 만큼 높아졌으며 RMSE 값의 경우 각각 0.331m, 0.111m 만큼 감소하였다. 그리고 관측정2의 경우 백록담 강수량 데이터를 추가적으로 사용 시 ANN 모델과 LSTM 모델은 NSE 값이 각각 0.012와 0.004 만큼 높아졌으며 RMSE 값의 경우 각각 0.073m, 0.025m 만큼 감소하였다. 즉, 본 연구 대상지역의 경우 백록담 강수량 데이터를 추가적으로 사용 시 인공지능 모델의 NSE 값은 최대 0.036만큼 개선되었다. 이 지하수위 예측 개선효과는 Fig. 10에서 직관적으로 확인할 수 있다. 따라서 관측정 상류지역에 위치한 백록담 강수량 데이터를 추가적으로 사용 시 인공지능 모델의 지하수위 예측성능은 개선되었으며 이것은 관측정 상류지역에서 침투한 강수가 하류지역에 위치한 관측정 지하수위에 영향을 미친다는 것을 의미한다. 또한 인공지능 모델은 관측정 상류지역의 강수량을 추가적으로 사용 시 지하수위의 변동특성을 더욱 적절히 해석할 수 있다는 것을 의미한다.

Table 5.

Impact of improving groundwater level prediction performance of artificial intelligence models when additionally using Baekrokdam precipitation data

Monitoring Well	Performance statistics	ANN_pBRD - ANN	LSTM_pBRD - LSTM
MW1	∆NSE	0.036	0.011
MW1	∆RMSE	-0.331	-0.111
MW2	∆NSE	0.012	0.004
MW2	∆RMSE	-0.073	-0.025

https://cdn.apub.kr/journalsite/sites/kwra/2024-057-10/N0200571003/images/kwra_57_10_03_F10.jpg

Fig. 10.

Comparison plots of one-month groundwater level predictions by artificial intelligence models for the entire observation well data period depending on whether or not to use additional Baekrokdam precipitation data (pBRD refers to the case of using Baekrokdam data)

주목할만한 점은 백록담 강수량 데이터를 추가적으로 사용 시 인공지능 모델의 지하수위 예측성능 개선효과가 지하수위 변동폭이 상대적으로 큰 관측정1에서 더 크게 나타난다는 점이다. Table 5에서 ANN 모델의 경우 백록담 강수량 데이터의 추가사용에 따른 NSE 값의 증가량은 관측정1에서 0.036을 보인 반면 관측정2에서 0.012를 보여 관측정1에 대한 지하수위 예측 개선효과는 관측정2의 경우 보다 3배를 나타내었다. LSTM 모델의 경우 NSE 값의 증가량은 관측정1에서 0.011을 보인 반면 관측정2에서 0.004를 보여 관측정1에 대한 지하수위 예측 개선효과는 관측정2의 경우 보다 약 2.8배를 나타내었다. RMSE 값의 경우에도 NSE 값의 경우와 비슷한 경향을 나타내었다. 이것은 지하수위 변동폭이 더 커 인공지능 모델의 지하수위 예측이 상대적으로 어려운 관측정의 경우 관측정 상류지역에 위치한 강우관측소 데이터의 추가사용 시 지하수위 예측 개선에 더욱 도움이 된다는 것을 의미한다.

또한 백록담 강수량 데이터를 추가적으로 사용 시 인공지능 모델의 지하수위 예측성능 개선효과는 지하수위 예측성능이 상대적으로 낮은 ANN 모델에서 더 크게 나타났다. Table 5에서 관측정1의 경우 백록담 강수량 데이터의 추가사용에 따른 NSE 값의 증가량은 ANN 모델이 0.036을 보인 반면 LSTM 모델이 0.011를 보여 ANN 모델의 지하수위 예측 개선효과는 LSTM 모델의 경우 보다 약 3.3배를 나타내었다. 관측정2의 경우 NSE 값의 증가량은 ANN 모델이 0.012을 보인 반면 LSTM 모델이 0.004를 보여 ANN 모델의 지하수위 예측 개선효과는 LSTM 모델의 경우 보다 3배를 나타내었다. RMSE 값의 경우에도 NSE 값의 경우와 비슷한 경향을 나타내었다. 이것은 지하수위 예측이 상대적으로 낮은 인공지능 모델일수록 관측정 상류지역에 위치한 강우관측소 데이터의 추가사용 시 지하수위 예측 개선에 더욱 도움이 된다는 것을 의미한다.

특히 백록담 강수량 데이터를 추가적으로 사용 시 ANN 모델의 지하수위 예측성능은 LSTM 모델과 대등한 수준으로 개선되었다. 관측정1에 대해 3.1절에서 기술하였듯이 백록담 강수량 데이터를 사용하지 않은 경우 LSTM 모델과 ANN 모델의 NSE 값의 차이는 0.026(0.897-0.871)을 보였으나 3.2절에서 기술하였듯이 백록담 강수량 데이터를 추가적으로 사용한 경우 LSTM 모델과 ANN 모델의 NSE 값의 차이는 0.001(0.908-0.907)로 크게 감소하였다. 이것은 특정 연구대상 지역의 경우 관측정 상류지역에 위치한 강우관측소 데이터를 추가적으로 사용 시 ANN 모델은 LSTM 모델의 예측 정확도 수준으로 지하수위를 예측할 수 있다는 것을 의미한다.

4. 결 론

본 연구에서는 제주도 남동쪽 표선유역 내 중산간 지역에 위치한 지하수위 변동폭이 상대적으로 크고 작은 2개 관측정을 대상으로 정확한 1개월 후 지하수위 예측을 위해 한라산 정상 부근에 위치한 백록담 기후변화관측소의 강수량 데이터를 추가적으로 사용하여 2개 인공지능 모델의 지하수위 예측성능 개선효과를 비교분석하였다. 분석 결과, 백록담 강수량 데이터를 추가적으로 사용하지 않은 경우 ANN 모델과 LSTM 모델은 2개 관측정 지하수위 예측성능이 NSE 값을 기준으로 0.871 이상을 보여 높은 예측성능을 나타내었다. LSTM 모델은 ANN 모델보다 고수위 및 저수위에서 상대적으로 높은 지하수위 예측성능을 보였으며, LSTM 모델은 제주도 중산간지역 지하수위 예측에 적합한 인공지능 모델로 판단된다. 또한, 관측지하수위의 변동폭이 크고 지하수위의 변동특성이 복잡할수록 인공지능 모델의 지하수위 예측은 어려워진다는 점을 확인하였다.

인공지능 모델에 백록담 강수량 데이터를 추가적으로 사용한 경우, ANN 모델과 LSTM 모델은 2개 관측정 지하수위 예측성능이 NSE 값을 기준으로 0.907 이상을 보여 더욱 개선된 매우 높은 예측성능을 나타내었다. 백록담 강수량 데이터를 추가적으로 사용한 경우 인공지능 모델의 NSE 값은 사용하지 않은 경우보다 최대 0.036만큼 개선되었다. 이것은 관측정 상류지역에서 침투한 강수가 하류지역에 위치한 관측정 지하수위에 영향을 미친다는 것을 의미하며, 인공지능 모델은 관측정 상류지역의 강수량 데이터를 추가적으로 사용 시 지하수위의 변동특성을 더욱 적절히 해석할 수 있다는 것을 의미한다. 또한 관측지하수위 변동폭이 더 커 인공지능 모델의 지하수위 예측이 상대적으로 어려운 관측정(관측정1)일수록 그리고 지하수위 예측성능이 상대적으로 낮은 인공지능 모델(ANN 모델)일수록 관측정 상류지역에 위치한 백록담 강수량 데이터의 추가사용 시 지하수위 예측 개선에 더욱 도움이 된다는 것을 확인하였다. 특히, 특정 관측정(관측정1)에 대해 백록담 강수량 데이터를 추가적으로 사용 시 ANN 모델의 지하수위 예측성능은 LSTM 모델과 대등한 수준으로 개선된다는 것을 확인하였다. 본 연구의 방법 및 결과는 향후 인공지능 모델을 활용한 연구에서 유용하게 사용될 수 있다.

Acknowledgements

본 연구는 제주지방기상청에서 백록담 기후변화관측소의 기상자료를 제공받아 연구에 사용하였습니다. 자료 제공에 감사드립니다.

Conflicts of Interest

The authors declare no conflict of interest.

References

Adamowski, J., and Chan, H.F. (2011). "A wavelet neural network conjunction model for groundwater level forecasting." Journal of Hydrology, Vol. 407, No. 1-4, pp. 28-40.

10.1016/j.jhydrol.2011.06.013

Alizamir, M., Kisi, O., and Zounemat-Kermani, M. (2018). "Modelling long-term groundwater fluctuations by extreme learning machine using hydro-climatic data." Hydrological Sciences Journal, Vol. 63, No. 1, pp. 63-73.

10.1080/02626667.2017.1410891

Barthel, R., and Banzhaf, S. (2016). "Groundwater and surface water interaction at the regional-scale - a review with focus on regional integrated models." Water Resources Management, Vol. 30, No. 1, pp. 1-32.

10.1007/s11269-015-1163-z

Bengio, Y., Simard, P., and Frasconi, P. (1994). "Learning long-term dependencies with gradient descent is difficult." IEEE Transactions on Neural Networks, Vol. 5, No. 2, pp. 157-166.

10.1109/72.27918118267787

Bizhanimanzar, M., Leconte, R., and Nuth, M. (2019). "Modelling of shallow water table dynamics using conceptual and physically based integrated surface-water - groundwater hydrologic models." Hydrology and Earth System Sciences, Vol. 23, No. 5, pp. 2245-2260.

10.5194/hess-23-2245-2019

Chollet, F., and Allaire, J.J. (2018). Deep learning with R. Manning Publications, Shelter Island, NY, U.S., p. 360.

Davoudi Moghaddam, D., Rahmati, O., Haghizadeh, A., and Kalantari, Z. (2020). "A modeling comparison of groundwater potential mapping in a mountain bedrock aquifer: QUEST, GARP, and RF models." Water, Vol. 12, No. 3, 679.

10.3390/w12030679

Falbel, D., Allaire, J.J., Chollet, F., Tang, Y., Van Der Bijl, W., Studer, M., Keydana, S. (2019). R Interface to 'Keras'. R Package Version 2.2.4.1, accessed 5 April 2019, <https://CRAN.R-project.org/package=keras>.

Fallah-Mehdipour, E., Haddad, O.B., and Mariño, M.A. (2013). "Prediction and simulation of monthly groundwater levels by genetic programming." Journal of Hydro-Environment Research, Vol. 7, No. 4, pp. 253-260.

10.1016/j.jher.2013.03.005

Gharehbaghi, A., Ghasemlounia, R., Ahmadi, F., and Albaji, M. (2022). "Groundwater level prediction with meteorologically sensitive Gated Recurrent Unit (GRU) neural networks." Journal of Hydrology, Vol. 612, 128262.

10.1016/j.jhydrol.2022.128262

Gholizadeh, H., Zhang, Y., Frame, J., Gu, X., and Green, C.T. (2023). "Long short-term memory models to quantify long-term evolution of streamflow discharge and groundwater depth in Alabama." Science of the Total Environment, Vol. 901, 165884.

10.1016/j.scitotenv.2023.16588437517717

Gong, Y., Zhang, Y., Lan, S., and Wang, H. (2016). "A comparative study of artificial neural networks, support vector machines and adaptive neuro fuzzy inference system for forecasting groundwater levels near Lake Okeechobee, Florida." Water Resources Management, Vol. 30, pp. 375-391.

10.1007/s11269-015-1167-8

Hahnloser, R.H., Sarpeshkar, R., Mahowald, M.A., Douglas, R.J., and Seung, H.S. (2000). "Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit." Nature, Vol. 405, No. 6789, pp. 947-951.

10.1038/3501607210879535

Haykin, S. (2009). Neural networks and learning machines, Pearson Prentice Hall, Upper Saddle River, NJ, U.S.

Hochreiter, S., and Schmidhuber, J. (1997). "Long short-term memory." Neural Computation, Vol. 9, No. 8, pp. 1735-1780.

10.1162/neco.1997.9.8.17359377276

Jeihouni, E., Mohammadi, M., Eslamian, S., and Zareian, M.J. (2019). "Potential impacts of climate change on groundwater level through hybrid soft-computing methods: a case study - Shabestar Plain, Iran." Environmental Monitoring and Assessment, Vol. 191, No. 10, 620.

10.1007/s10661-019-7784-631493149

Jeju Special Self-Governing Province (JSSGP) (2022). Basic plan for integrated water management for Jeju Special Self-Governing Province. pp. 1-485.

Jha, M.K., and Sahoo, S. (2014). "Efficacy of neural network and genetic algorithm techniques in simulating spatio‐temporal fluctuations of groundwater." Hydrological Processes, Vol. 29, No. 5, pp. 671-691.

10.1002/hyp.10166

Kim, D., Jang, C., Choi, J., and Kwak, J. (2023). "A case study: Groundwater level forecasting of the gyorae area in actual practice on jeju island using deep-learning technique." Water, Vol. 15, No. 5, 972.

10.3390/w15050972

Kim, I., and Lee, J. (2022). "Performance analysis of ANN prediction for groundwater level considering regional- specific influence components." Groundwater, Vol. 60, No. 3, pp. 344-361.

10.1111/gwat.1315634873680

Kim, T.W., and Valdés, J.B. (2003). "Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks." Journal of Hydrologic Engineering, Vol. 8, No. 6, pp. 319-328.

10.1061/(ASCE)1084-0699(2003)8:6(319)

Kingma, D.P., and Ba, J. (2014). "Adam: A method for stochastic optimization." arXiv preprint arXiv:1412.6980.

Kow, P.Y., Liou, J.Y., Sun, W., Chang, L.C., and Chang, F.J. (2024). "Watershed groundwater level multistep ahead forecasts by fusing convolutional-based autoencoder and LSTM models." Journal of Environmental Management, Vol. 351, 119789.

10.1016/j.jenvman.2023.11978938100860

Lallahem, S., Mania, J., Hani, A., and Najjar, Y. (2005). "On the use of neural networks to evaluate groundwater levels in fractured media." Journal of Hydrology, Vol. 307, No. 1-4, pp. 92-111.

10.1016/j.jhydrol.2004.10.005

Le, X.H., Ho, H.V., Lee, G., and Jung, S. (2019). "Application of long short-term memory (LSTM) neural network for flood forecasting." Water, Vol. 11, No. 7, 1387.

10.3390/w11071387

Maier, H.R., and Dandy, G.C. (2000). "Neural networks for the prediction and forecasting of water resources variables: a review of modelling issues and applications." Environmental Modelling & Software, Vol. 15, No. 1, pp. 101-124.

10.1016/S1364-8152(99)00007-9

McDonald, M.G., and Harbaugh, A.W. (1988). A modular three-dimensional finite-difference ground-water flow model. Vol. 6. US Geological Survey, Reston, VA, U.S.

Mirarabi, A., Nassery, H.R., Nakhaei, M., Adamowski, J., Akbarzadeh, A.H., and Alijani, F. (2019). "Evaluation of data-driven models (SVR and ANN) for groundwater-level prediction in confined and unconfined systems." Environmental Earth Sciences, Vol. 78, No. 15, pp. 1-15.

10.1007/s12665-019-8474-y

Mohanty, S., Jha, M.K., Kumar, A., and Panda, D.K. (2013). "Comparative evaluation of numerical model and artificial neural network for simulating groundwater flow in Kathajodi - Surua Inter-basin of Odisha, India." Journal of Hydrology, Vol. 495, pp. 38-51.

10.1016/j.jhydrol.2013.04.041

Mohanty, S., Jha, M.K., Kumar, A., and Sudheer, K.P. (2010). "Artificial neural network modeling for groundwater level forecasting in a river island of eastern India." Water Resources Management, Vol. 24, pp. 1845-1865.

10.1007/s11269-009-9527-x

Moriasi, D.N., Arnold, J.G., Van Liew, M.W., Bingner, R.L., Harmel, R.D., and Veith, T.L. (2007). "Model evaluation guidelines for systematic quantification of accuracy in watershed simulations." Transactions of the ASABE, Vol. 50, No. 3, pp. 885-900.

10.13031/2013.23153

Müller, J., Park, J., Sahu, R., Varadharajan, C., Arora, B., Faybishenko, B., and Agarwal, D. (2021). "Surrogate optimization of deep neural networks for groundwater predictions." Journal of Global Optimization, Vol. 81, No. 1, pp. 203-231.

10.1007/s10898-020-00912-0

Nash, J.E., and Sutcliffe, J.V. (1970). "River flow forecasting through conceptual models part I - A discussion of principles." Journal of Hydrology, Vol. 10, No. 3, pp. 282-290.

10.1016/0022-1694(70)90255-6

Payne, K., Chami, P., Odle, I., Yawson, D.O., Paul, J., Maharaj-Jagdip, A., and Cashman, A. (2022). "Machine learning for surrogate groundwater modelling of a small carbonate island." Hydrology, Vol. 10, No. 1, 2.

10.3390/hydrology10010002

Prechelt, L. (2012) "Early stopping - but when?" Neural networks: tricks of the trade, Edited by Montavon, G., Orr, G.B., and Müller, KR., Springer, Heidelberg, Germany, pp. 53-67.

10.1007/978-3-642-35289-8_5

Rajaee, T., Ebrahimi, H., and Nourani, V. (2019). "A review of the artificial intelligence methods in groundwater level modeling." Journal of Hydrology, Vol. 572, pp. 336-351.

10.1016/j.jhydrol.2018.12.037

Rakhshandehroo, G.R., Vaghefi, M., and Aghbolaghi, M.A. (2012). "Forecasting groundwater level in Shiraz plain using artificial neural networks." Arabian Journal for Science and Engineering, Vol. 37, No. 7, pp. 1871-1883.

10.1007/s13369-012-0291-5

Rumelhart, D.E., Hinton, G.E., and Williams, R.J. (1986). "Learning representations by back-propagating errors." Nature, Vol. 323, No. 6088, pp. 533-536.

10.1038/323533a0

Sahoo, S., Russo, T.A., Elliott, J., and Foster, I. (2017). "Machine learning algorithms for modeling groundwater level changes in agricultural regions of the US." Water Resources Research, Vol. 53, No. 5, pp. 3878-3895.

10.1002/2016WR019933

Seidu, J., Ewusi, A., Kuma, J.S.Y., Ziggah, Y.Y., and Voigt, H.J. (2023). "Impact of data partitioning in groundwater level prediction using artificial neural network for multiple wells." International Journal of River Basin Management, Vol. 21, No. 4, pp. 639-650.

10.1080/15715124.2022.2079653

Seifi, A., Ehteram, M., Singh, V.P., and Mosavi, A. (2020). "Modeling and uncertainty analysis of groundwater level using six evolutionary optimization algorithms hybridized with ANFIS, SVM, and ANN." Sustainability, Vol. 12, No. 10, 4023.

10.3390/su12104023

Shin, M.J., Kim, J.W., Moon, D.C., Lee, J.H., and Kang, K.G. (2021). "Comparative analysis of activation functions of artificial neural network for prediction of optimal groundwater level in the middle mountainous area of Pyoseon watershed in Jeju Island." Journal of Korea Water Resources Association, Vol. 54, No. 12, pp. 1143-1154.

Shin, M.J., Moon, S.H., Kang, K.G., Moon, D.C., and Koh, H.J. (2020). "Analysis of groundwater level variations caused by the changes in groundwater withdrawals using long short-term memory network." Hydrology, Vol. 7, No. 3, 64.

10.3390/hydrology7030064

Sit, M., Demiray, B.Z., Xiang, Z., Ewing, G.J., Sermet, Y., and Demir, I. (2020). "A comprehensive review of deep learning applications in hydrology and water resources." Water Science and Technology, Vol. 82, No. 12, pp. 2635-2670.

10.2166/wst.2020.36933341760

Sun, J., Hu, L., Li, D., Sun, K., and Yang, Z. (2022). "Data-driven models for accurate groundwater level prediction and their practical significance in groundwater management." Journal of Hydrology, Vol. 608, 127630.

10.1016/j.jhydrol.2022.127630

Sun, Y., Wendi, D., Kim, D.E., and Liong, S.Y. (2016). "Application of artificial neural networks in groundwater table forecasting - a case study in a Singapore swamp forest." Hydrology and Earth System Sciences, Vol. 20, No. 4. pp. 1405-1412.

10.5194/hess-20-1405-2016

Tao, H., Hameed, M.M., Marhoon, H.A., Zounemat-Kermani, M., Heddam, S., Kim, S., Sulaiman, S.O., Tan, M.L., Sa'adi, Z., Mehr, A.D., Allawi, M.F., Abba, S.I., Zain, J.M., Falah, M.W., Jamei, M., Bokde, N.D., Bayatvarkeshi, M., Al-Mukhtar, M., Bhagat, S.K., Tiyasha, T., Yaseen, Z.M. (2022). "Groundwater level prediction using machine learning models: A comprehensive review." Neurocomputing, Vol. 489, pp. 271-308.

10.1016/j.neucom.2022.03.014

Yin, J., Medellín-Azuara, J., Escriva-Bou, A., and Liu, Z. (2021). "Bayesian machine learning ensemble approach to quantify model uncertainty in predicting groundwater storage change." Science of The Total Environment, Vol. 769, 144715.

10.1016/j.scitotenv.2020.14471533736244

Journal of Korea Water Resources Association ISSN:2799-8746(Print) 2799-8754(Online) 한국수자원학회 논문집

Preview

Impact of Baekrokdam precipitation observation data on improving groundwater level prediction in mid-mountainous region of Jeju Island

ABSTRACT

MAIN

Fig. 1.

Schematic diagram of the locations of precipitation observation stations, groundwater withdrawal wells, and groundwater level monitoring wells

Table 1.

Period of precipitation, groundwater withdrawal and groundwater level data

Fig. 2.

Precipitation time series data from Baekrokdam, Seongpanak, and Gyorae precipitation observation stations

Fig. 3.

Comparison of precipitation at Baekrokdam, Seongpanak, and Gyorae precipitation observation stations

Fig. 4.

Groundwater level fluctuation range of groundwater level monitoring wells

Fig. 5.

The structure of ANN model (Shin et al., 2021)

(1)

(2)

Fig. 6.

The structure of LSTM model (Shin et al., 2020)

(3)

(4)

(5)

(6)

Fig. 7.

Groundwater level learning procedure of artificial intelligence models (Shin et al., 2021)

Table 2.

Hyper-parameters of artificial intelligence models

(7)

(8)

Table 3.

Statistics on the one-month groundwater level prediction performance of artificial intelligence models for the entire observation well data period when excluding Baekrokdam precipitation data

Fig. 8.

Artificial intelligence models' one-month groundwater level prediction plots for the entire observation well data period when excluding Baekrokdam precipitation data

Table 4.

Statistics on the one-month groundwater level prediction performance of artificial intelligence models for the entire observation well data period when including Baekrokdam precipitation data

Fig. 9.

Artificial intelligence models' one-month groundwater level prediction plots for the entire observation well data period when including Baekrokdam precipitation data

Table 5.

Impact of improving groundwater level prediction performance of artificial intelligence models when additionally using Baekrokdam precipitation data

Fig. 10.

Comparison plots of one-month groundwater level predictions by artificial intelligence models for the entire observation well data period depending on whether or not to use additional Baekrokdam precipitation data (pBRD refers to the case of using Baekrokdam data)

Acknowledgements

Conflicts of Interest

References