1. 서 론

하천이나 인공수로와 같은 개수로에 자생하는, 또는 인위적으로 심은 식생은 생태적, 심미적으로 고유한 역할을 하는 귀중한 자원이다. 또한 많은 경우 하천이나 호수의 수질개선에 기여한다. 그러나 하천식생은 수리적 관점에서 흐름에 추가적인 저항을 주고 그에 따라 같은 유량조건에서 하천수위를 높이기 때문에 하천관리의 주요 대상이다. 즉 과도한 식생은 하상재료의 거친 정도나 기타 자연적 흐름저항 요인에 추가되어 하천의 통수능을 저하시켜 홍수위험이 증가된다. 이런 이유로 개수로 수리학 연구가 체계적으로 시작된 1950년대부터 전문 개수로 수리학 책에서는 식생에 의한 추가적인 흐름저항에 대해 각별한 관심을 두었다. 구체적으로, 식생상황을 간단히 서술하거나 실제 식생하천 사진을 보여주면서 그에 해당하는 흐름저항을 Manning의 조도계수 n (이후 매닝계수라 함)으로 제시하였다(Chow, 1959). 그러나 이러한 식생상황의 정성적 기술이나 관련 사진에 의한 흐름저항 추정치는 경험적, 주관적일 수밖에 없어 과학적인 수위-유량관계나 유량-유사량 관계를 정립하고 현지여건에 맞는 수리계산을 하는 데는 분명한 한계가 있었다.

본 연구의 목적은 하천홍수 관리 차원에서 문제가 되는 하천식생의 흐름저항 연구에 대해 연혁부터 시작하여 최근 연구성과까지 체계적으로 검토하여 독자들에게 핵심적인 정보를 제공하는 것이다.

본 연구는 하천식생을 물리적 특성 차원에서 단단한(rigid) 것과 유연한(flexible) 것으로 나누고, 이 모두에 대해 다시 물 아래 침수된(submerged) 것과 물위 정수(挺水)된(emergent) 것으로 나누어서 검토한다. 한편 식생의 위치에 따라 홍수터식생과 하도식생으로 나뉘고, 홍수터식생은 본 연구의 주대상이 되며, 하도식생은 수생식물(aquatic plant)만 가능하기 때문에 별도 간단히 검토한다. 본 연구에서는 하도 내 모래사주 등에 형성된 식생 또한 홍수터식생으로 간주한다. 마지막으로 식생의 분포 특성을 기준으로 비교적 큰 범위에 걸쳐 단일종이나 2~3개 종이 균일 분포하는 상태(경관생태학 용어로 매트릭스 또는 바탕)와 하도나 홍수터에서 일정방향으로 연달아 이어지는 상태(경관생태학 용어로서 패치 또는 조각)를 구분하여 검토한다.

본 연구는 우선 하천식생의 흐름저항 연구성과를 총설적으로 발표한 논문 등을 중심으로 검토하고, 관련 개별 논문도 검토하여 상호 보완한다. 특히 해외 관련논문을 우선적으로 검토하고 국내 논문도 검토한다. 이러한 관련 연구의 심층검토 결과를 가지고 현 하천실무에 추천사항 및 향후 연구방향을 제시한다. 마지막으로 본 연구에서 빈번히 사용되는 주요 용어를 정의하고 시작하는 것이 독자들의 이해에 도움이 될 것이다. 하천식생, 또는 수변식생(riparian vegetation)은 하천에 자생하거나 식재한 식물군을 통칭하며, 여기서 하천은 하도, 강턱(river bank), 홍수터, 사주 등을 포함한다. 따라서 하천식생은 이러한 하천구역, 또는 경관생태학적으로 하천회랑(river corridor)에 자라는 식물군이다. 흐름저항은 물과 하상경계면 간 마찰이나 기타 항력에 의한 저항을 망라한다. 한편 조도는 흐름저항을 일으키는 물리적 요인의 ‘거친’ 정도를 나타내며, 크게 사립조도(grain roughness), 형상조도(form roughness), 하도조도(channel roughness) 등으로 나뉜다(Woo et al., 2015). 이동 하상에서는 흐름저항이 사립자의 크기에 직접 관련이 있는 사립조도에 의한 저항과 하상형태와 그 변화에 의한 형상조도에 의한 저항으로 구분할 수 있다(Woo et al., 2015). 하도조도는 만곡, 사주, 기타 하폭 규모의 하천지형에 의한 흐름저항을 의미한다. 식생조도(vegetative roughness)는 위 같은 조도에 추가하여 식생에 의해 나타나는 조도이다. 마지막으로 흐름저항계수(flow resistance coefficient)는 위와 같은 다양한 요인에 의한 흐름저항을 총체적으로 나타내는 계수이며(Yen, 2002), Darcy-Weisbach의 f와 같은 마찰계수(friction factor), Manning의 n과 같은 조도계수, Chezy의 C와 같은 계수로 환산하여 표시할 수 있다.

2. 해외의 연구연혁

흐름에 의한 경계면 마찰은 다음과 같은 기본적인 관계식부터 시작한다.

여기서 f, R, n, g, C, V, S는 각각 Darcy-Weisbach의 마찰계수, 수리반경, 매닝계수, 중력가속도, Chezy 계수, 평균유속, 에너지경사이다. 참고로 Eq. (1)에 의하면 Darcy-Weisbach의 마찰계수 f는 무차원 수이며, 매닝계수 n은 [L-1/3T], 체지계수 C는 [L1/2T]의 차원을 갖는다. Corenblit et al. (2007)은 1950년대 이후 식생에 의한 흐름저항관련 주요 연구진행 상황을 1) Cowan (1956) 연구 같은 간단한 하천상태기술 방법, 2) Barnes (1967)과 같은 하천사진제시 방법, 3) Li and Shen (1973)과 같은 단단한 식생에 의한 흐름저항 모형, 4) Kouwen and Unny (1973) 같은 유연한 식생에 의한 흐름저항 모형 등으로 나누어 총 14개의 연구를 소개하고 있다. 본 연구도 이러한 구분에 준하여 검토한다.

2.1 도표식 경험적 접근법과 문제점

개수로는 관수로와 달리 경계면 마찰에 의한 흐름저항 뿐만 아니라 하상형태, 하도형상, 식생 등에 의한 추가적인 저항요소가 있기 때문에 자연하천이나 인공수로에서 흐름저항은 매닝계수나 Chezy 계수에 개별적인 저항 및 에너지 손실을 모두 합하는 경험적 접근법에서 크게 벗어나지 못하였다. 그 대표적인 예가 다음과 같은 Cowan (1956)의 매닝계수 합산식이다.

여기서 nb는 균일하고 매끈한 수로(prismatic channel)에서 경계면 마찰에 의한 기본 조도계수이며, n1은 하상형태에 따른 수로표면의 불균일성에 대한 보정치, n2는 수로단면의 형상과 크기에 따른 보정치, n3은 흐름장애물에 대한 보정치, n4는 식생과 흐름조건에 따른 보정치이며, m은 수로만곡에 대한 보정치이다. 여기서 특히 식생과 흐름조건에 대한 보정치 n4는 다양한 흐름과 식생 상태를 과학적으로 고려하여 추정할 수 있는 방법론이 없었기 때문에 앞서 소개한 경험적 자료와 대표 수로사진과 비교하여 조도계수를 추정하는 1950년대 말 Chow 식 접근법이 세계적으로 통용되었다. Barnes (1967)에 의해 제안된 자연하천 조도계수 추정방법도 기본적으로 Chow 식 접근법을 따르고 있다. 이와 같이 대표사진과 비교하는 방법 이외에 1980년대 말 USGS에서는 하천의 식생량을 소량, 중량, 대량, 초대량 네 등급으로 나누고 각각의 등급을 수심과 식생고의 비율을 기준으로 임의로 정하고, 각각의 등급에 해당하는 매닝계수의 범위를 0.001~0.2까지 주었다(George and Schneider, 1989). 한편 Arcement and Schneider (1989)는 실무에 직접 참고할 수 있도록 홍수에 취약하고 식생이 가득한 15개 지역의 하천사진과 관련 조도계수 자료를 제시하였다. 1990년대 들어 Masterman and Thorne (1992)는 하천 홍수관리 측면에서 식생에 대한 부정적인 인식은 주로 Chow와 Barnes 등의 식생에 의한 과다한 매닝계수 값에 기인한 것으로 보았다. 한 예로 Chow는 보통의 모래나 자갈 수로에 매닝계수로 0.03을 부여한 반면에, 바닥이 불규칙적이고 강턱에 갯버들이나 포플러 등이 자생하는 경우 0.08을 부여하였다. 이 경우 수리계산 결과 80% 정도의 수위증가를 보여준다. 그러나 Masterman and Thorne (1992)는 Darcy-Weiswach의 마찰계수(f)를 이용한 이론적 수리계산을 통해 강턱 식생이 주는 흐름저항은 기존에 인식한 것만큼 크지 않는 것으로 보여주었다. 구체적으로, 나무높이가 0.8 m로 수심 정도이고 식생밀도가 높은 강턱의 경우 하폭과 수심의 비가 9보다 작아야 통수능은 5% 이상 작아지는 것으로 나타났다. 또한 처음에 흐름에 저항하지 못하는 풀이 자라다 나중에 갯버들과 같은 나무가 자라는 경우에도 폭과 수심의 비가 16 이상이 되어도 통수능은 10% 이하로 감소하는 것으로 산정되었다. 홍수터 식생이 전체 하도의 홍수위 상승에 미치는 효과는 전통적으로 생각해온 것보다 의외로 작다는 사실은 국내 Kim et al. (2010)의 연구에서도 나타났다.

2.2 해석적 방법

D’Ippolito et al. (2021)의 연구는 본 연구주제와 일관된 몇 안 되는 총설논문으로서, 그들은 식생에 의한 흐름저항 연구 연혁을 1) 서술 및 사진을 통한 비교 방법, 2) 해석적 방법, 3) 수치해석(난류해석) 등으로 나누어 검토하였다. 여기서 1) 방법은 전술한 Chow나 Barnes의 방법을 말하며, 2) 방법은 단단한 식생과 유연한 식생으로 나누고 다시 각각에 대해 ‘침수’(submerged) 식생과 ‘정수’(emergent) 식생으로 구분하는 것이다.

침수와 정수 조건은 두 조건 하에서 유속의 연직분포가 완전히 달라지기 때문에 중요하다. Nepf and Vivoni (2000)는 완전 침수조건으로 수심 h와 식생높이 hv의 비, hhv≫5를 기준하였으며, 잔디와 같은 초본류 위를 깊이 흐르는 흐름 등이 이에 해당될 것이다. 이 경우 식생에 의한 흐름저항은 식생 자체를 하상재료와 같은 조도로 보고 앞서 설명한 전통적인 도표식 방법으로 조도계수를 추정할 수 있을 것이다. 다음은 hv>h 인 경우로서 식생이 물 위로 나온 경우로서, 나중에 설명할 Fig. 1에 해당한다. 세번 째가 5hv>h>hv의 경우로서 식생이 물 속에 충분히 잠긴 경우이다. 이는 나중에 설명할 Fig. 2에 해당한다. 본 연구는 D’Ippolito et al. (2021)의 구분에 준하여 관련된 연구성과를 검토한다.

이 절에서는 위에 설명하였듯이 식생과 수심의 상대적 높이와 식생줄기의 물리적 성질 등을 기준으로 모두 넷으로 나누어 검토한다. 여기서 거의 모든 모형에 공히 적용되는 식생에 의한 흐름저항 FD는 다음과 같이 표시된다.

여기서 CD는 항력계수로서 아무 정보가 없는 경우 보통 1.0으로 가정하며, 𝜌는 물의 밀도, Ap는 흐름방향에 투영된 저항체 면적이다. 이 식에서 실제 추정이 어려운 변수는 항력계수와 식생의 투영면적이다. 이 두 인자는 흐름조건에 따라 변하기 때문에 식생에 의한 흐름저항도 흐름에 따라 달라진다. 즉 식생과 흐름은 상호작용을 한다. 여기서 비교적 간단히 접근할 수 있는 흐름 및 식생 조건은 다음과 같이 등류조건에서 식생을 전봇대 같은 단단한 기둥으로 보고 접근하는 것이다.

2.2.1 정수, 단단한 식생(Emergent, rigid vegetation)

물 위로 나온, 단단한 식생 모형은 Fig. 1과 같이 수로바닥에 원통형 나무가 일정하게 배열된 것으로서, 해석적 접근이 가능하다. 즉 개별 식생(수목)을 균일한 원통으로 가정하고 수로 상하류에 운동량방정식을 적용하고 Eq. (3)에서 다양한 CD 조건 별 흐름계산을 하는 방법이다. D’Ippolito et al. (2021)은 문헌조사를 통해 위와 같은 방법으로 접근한 다양한 항력계수 방정식을 Ishikawa et al. (2000)을 포함하여 모두 8개 식을 소개하고 있다. 이 같은 다양한 항력계수 값은 0.5~2.0 범위인 것으로 나타났다.

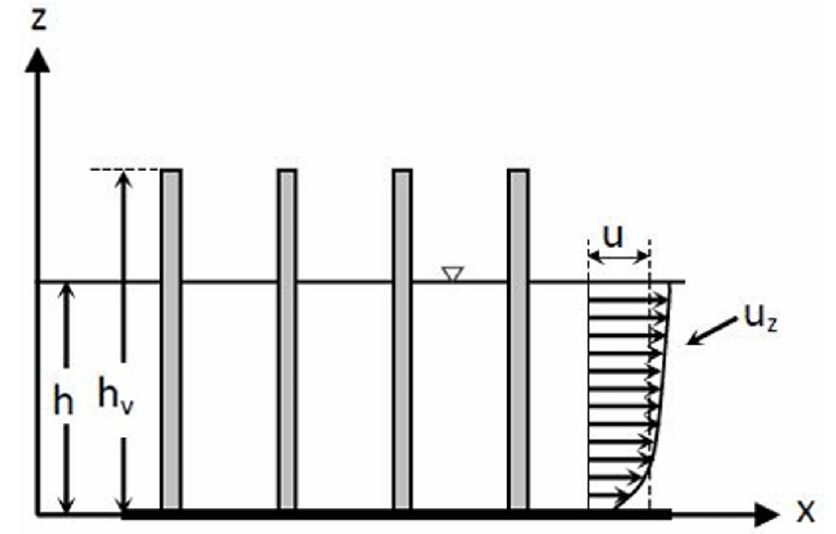
Fig. 1.

Schematic view of submerged rigid vegetation model (h: water depth, hv: vegetation height, u: mean velocity, uz: velocity profile)(Excerpted from D’Ippolito et al., 2021; Fig. 3)

한편 식생항력을 포함한 운동량방정식을 적용하면 식생저항에 상당하는 조도계수로 매닝계수나 Chezy 계수를 구할 수 있다. 식생하천의 매닝계수에 대해서는 일찍이 Petryk and Bosmajian (1975)이 이른바 식생밀도방법(vegetation-density method)이라 하여 등류 조건에서 수로 바닥마찰에 의한 저항과 식생에 의한 저항이 흐름방향 물의 중력과 균형을 이루는 운동량방정식을 적용하여 경계면 및 식생 모두에 의한 매닝계수를 다음과 같이 유도하였다.

위 식에서 nb는 하상이나 홍수터의 경계면 마찰에 의한 매닝계수이며, ∑Ai는 흐름방향으로 수목의 투영면적의 합이며, A는 통수단면적, L은 하천구간 거리이다.

Petryk and Bosmajian (1975)의 관계식은 나중에 침수흐름과 정수흐름 모두에 대해 확장되었으며, 이 분야의 선구자 중 하나인 Tsujimoto (1999)과 Wu et al. (1999) 등에 의해 실험을 통해 검증되었다. 이러한 관계식에서는 수목의 밀도, 직경, 배치 등과 수목높이와 수심의 비 등이 식생흐름 동역학에 밀접히 관련되어 있다. 예를 들면 흐름 마찰계수 f와 수목(원통형 기둥)의 밀도는 양의 상관성을 보이며(Ishikawa et al., 2003), 어느 실험에서는 50%의 밀도 증가는 50%의 마찰계수 증가를 가져오지만 수심이 동시에 증가하게 되어 일관되게 증가하지 않는 것으로 나타났다(Järvelä, 2002).

정수 식생하천의 Chezy 계수에 대해서 Baptist et al. (2007)은 다음과 같이 표시하였다.

위 식에서 Cb는 하상이나 홍수터의 경계면 마찰에 의한 Chezy 계수이며, m은 수목의 수, D는 수목의 직경이다. Eq. (5)는 이탈리아 북서부 Magra 강에서 발생한 2011년 대홍수의 주요 원인으로 지목된 수변식생 영향을 과학적으로 검토하기 위해 Delft3D-FLOW 모형의 입력자료로 이용되었다(Benifei et al., 2015).

한편 식생투영면적을 나타내기 위해 잎면적지수(Leaf Area Index, LAI) 개념을 사용한 Järvelä (2004) 공식은 ‘단단한 기둥’ 모형에 입각하여 개발된 다른 공식들과 비슷한 예측결과를 보였다. 여기서 LAI는 지상 단위면적(m²) 당 식생의 잎 면적의 합(m²)을 나타내는 지수이다. 이 연구는 1차원 하천모형에서 관목이나 교목 등이 물에 완전히 잠기기 전까지는 ‘단단한 기둥’ 가정에 의한 흐름저항 추정 방법론이 실용성이 있음을 보였다. 그러나 물에 완전히 잠긴 후 부터는 식생의 줄기 및 가지, 잎 등의 재배열(reconfiguration)로 해석적 접근은 더 어려워진다.

물 위로 나온 단단한 식생 조건은 일찍부터 실험실에서 연구되어 왔기 때문에 문헌상 자료가 상대적으로 풍부하고, 이에 따라 이러한 풍부한 자료를 이용한 경험적 접근도 시도되었다. D’Ippolito et al. (2019)는 선형적으로 배열된 물 위로 나온 단단한 식생군을 대상으로 항력계수 CD를 식생밀도의 함수로 표시된 간단한 경험식을 제시하였다. 그 후 D’Ippolito et al. (2024)는 이 경험식에 유효수로 폭 개념을 이용하여 수면곡선을 계산하고 실험실 실측치와 비교하여 공식의 효용성을 확인하였다.

마지막으로 Liu et al. (2020)은 Genetic Programming과 Machine Learning 기법을 문헌에 공개된 자료에 적용하여 정수 조건에서 단단한 식생이 일정하게 나열된 경우 저항계수식을 도출하였다. 이들이 여기에 사용한 인자는 차폐계수(blockage factor), 식생밀도, 그리고 레이놀즈 수이다.

2.2.2 침수, 단단한 식생(Submerged, rigid vegetation)

Fig. 2와 같이 침수된 단단한 식생의 경우 유속분포는 크게 아래 식생층과 위 표면층으로 구분되며, 이 두 층은 변곡점으로 연결된다. 식생층에서 흐름은 정수 조건의 경우와 비슷하며(Liu et al., 2008), 표면층에서 흐름은 자유흐름이 된다. 그러나 두 층의 속도차이로 경계면에서 전단층이 형성되며 여기서 발생하는 소용돌이(vortex)는 하류로 갈수록 커진다.

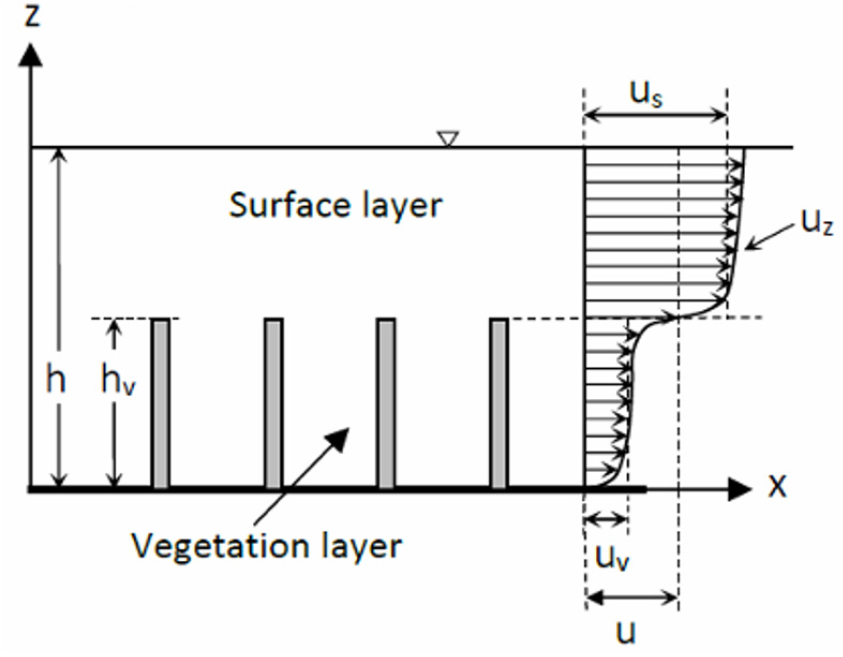
Fig. 2.

Schematic view of submerged rigid vegetation model (uv: average velocity at vegetation layer, us: average velocity at surface layer, u: average velocity at whole cross section, uz: point velocity at z)(Excerpted from D’Ippolito et al., 2021; Fig. 5)

이 분야는 실험과 난류해석을 통해 각 층별 유속분포 및 평균유속 등 많은 연구가 수행되었으며, D’Ippolito et al. (2021)은 Chezy 계수와 매닝계수를 구하는 식으로 이 분야에서 다양한 연구를 수행한 Baptist et al. (2007)과 국내연구인 Yang and Choi (2010) 등 4개의 공식을 소개하고 있다. Cheng (2011)은 위 4개 식을 비교 평가하여 다양한 흐름 조건에서 그들의 식이 상대적으로 우수함을 보였다. 한편, Li et al. (2015)는 흐름의 아래층은 ‘기본층’, 위층은 ‘부유층’으로 구분하고 부유층에서 식생영향을 유효상대조고로 표시한 다음 매닝계수나 Chexy 계수 등으로 표시된 마찰계수를 유도하였다. 이들은 기존 측정자료를 이용하여 Stone and Shen (2002) 공식 등 5개의 공식과 비교하여 개발된 공식의 타당성을 보였다.

Chen et al. (2023)은 Petryk and Bosmajian (1975)의 식생밀도방법을 기준으로 침수 및 정수 조건의 단단한 식생에 대해 운동량방정식을 적용하여 매닝계수를 유도하였다. 그들은 Shimizu et al. (1991) 등 10개의 기존 식생흐름저항 실험자료에 유도된 매닝계수 식을 적용하여 비교적 양호한 결과를 보여주었다. 그들이 제안한 공식은 물리적 법칙에 기본을 둔 해석적인 방법으로, 그들의 공식에 필요한 식생계수는 야외에서 비교적 쉽게 얻을 수 있는 단단한 식생에 국한되며, 유연한 식생의 경우 도출이 어려워 적용성이 떨어진다.

2.2.3 정수, 유연한 식생(Emergent, flexible vegetation)

유연한 식생은 초본류나 일부 관목류, 그리고 교목의 잔가지(twig)와 같이 흐름에 쉽게 휘는 식생을 말한다. 이 경우 식생의 휨 정도가 마찰저항 및 평균유속에 영향을 준다. 완전히 침수되지 않은, 정수 상태의 유연한 식생에 의한 흐름저항 연구는 침엽수나 포플러, 버드나무 등과 같이 홍수터에 자생하거나 식재한 수목에 의한 흐름저항에 초점을 맞춘다. 이러한 식생, 특히 버드나무류와 흐름 간 상호작용 형태는 안동시의 낙동강 구간(Egger et al., 2012)이나 섬진강 구간(Lee et al., 2023) 등 국내에 흔히 나타나며, 또한 관목이나 교목이 초본류보다는 상대적으로 더 큰 흐름저항을 주기 때문에 이 문제는 국내에서 상대적으로 중요하다. Fig. 3은 이러한 상태를 도식적으로 보여준다.

Fig. 3.

Schematic view of emergent flexible vegetation model (drawn in this study)

이 분야 연구는 식생에 의한 흐름저항을 대부분 f 값으로 표시하지만, 일부 경험공식을 이용하여 n 값으로 표시하는 연구도 있다(Freeman et al., 2000). 이 분야에서는 Kouwen 연구그룹과 Järvelä and Västilä 연구그룹의 성과가 중요하다. Fathi-Maghadam and Kouwen (1997)은 물 밖에 나온 유연한 식생에 대한 실험연구에서 식생의 유연성이 유속이 증가함에 따라 잎 면적(Momentum Absorbing Area, MAA)의 처짐과 항력계수의 감소에 큰 영향을 준다는 것을 확인했다. 이 조건에서 매닝계수는 수심의 제곱근에 비례하여 증가한다는 것을 보여주었다. 그 이유로 수심에 따라 물속에 잠기는 MAA가 증가하기 때문이다. 그들은 이러한 조건에서 식생밀도가 흐름저항의 주요 지배인자라고 결론지었다. 나아가 Kouwen and Fathi-Moghadam (2000)은 물과 공기 흐름을 이용한 실험을 통해 자료를 수집하고 흐름과 식생(수목)의 다양한 조건에서 차원해석을 통해 Darcy-Weisbach의 마찰계수 f 값을 추출하였다. 여기서 마찰계수는 식생의 변형에 관련된 계수 𝜉와 탄성계수 E 값의 곱(ξE)과 상대수심(h/hv)로 나타냈다.

Järvelä (2002)의 광범위한 실험에 의하면 포플러나 버드나무 같이 상대적으로 단단한 줄기와 유연한 잔가지와 잎으로 구성된 식생의 항력에 가장 크게 기여하는 것은 잎에 의한 항력이며, 이는 잎이 넓든 길쭉한 모양이든 관계없는 것으로 나타났다. 잎이 달린 버드나무의 식생 마찰계수 f는 잎이 없는 경우보다 무려 3배 가까이 큰 것으로 나타났다. 한편 Västilä et al. (2013)은 잎이 달린 포플러 나무에 의한 흐름저항을 평가하기 위해 나무의 특성에 대한 4개의 특성 참조면적을 이용하였다. 즉, 가지에 달린 잎의 총 면적 AL, 줄기의 투영면적 AS, 흐름상태에서 수목의 투영면적 AP, 공기 중 수목의 투영면적 A0 등의 변수를 가지고 실험실 수로 바닥에 잎이 달린 가지를 고정하고 실험을 수행하여 마찰계수를 평가하였다. 그 결과 잎/줄기 참고면적 비율인 AL/AS이 식생 흐름저항에 가장 크게 영향을 주는 것으로 나타났다.

물에 잠기거나, 물 위로 나온 유연한 식생 모두에 적용할 수 있다는 모형 중 하나가 Luhar and Nepf (2013)의 해석적 모형이다. 그들은 식생군을 식물잎이나 식물줄기 하나만 고려하는 개별식생 규모(blade scale), 줄지어 있는 식생군을 대상으로 하는 패치 규모(patch scale), 그리고 한 하도의 일정 구간 전체를 대상으로 하는 구간 규모(reach scale)로 구분하였다(Fig. 4). 그들은 흐름에 의한 식생변형을 반복계산으로 고려하였다. 마지막으로 하천의 구간 규모에 적용할 수 있는 매닝계수 산정식을 그 구간 내에 있는 모든 패치에 의한 차폐효과인 이른바 차폐계수 또는 차단지수(blockage factor)로 제시하였다. 그러나 그들도 지적하였듯이 차폐계수 하나만으로 식생패치의 배열에 따른 흐름저항 변화를 충분히 반영하지 못한다. 여기서 한 단면에서 차폐계수는 흐름 단면적에 대한 식생 단면적의 비율을 의미한다(Green, 2005). 구간 규모에 대한 차폐계수는 구간 내 흐름 전체부피에 대해 상하류 두 흐름단면에서 식생 단면적 평균 값에 두 단면 간 거리를 곱하여 나온 부피를 모두 더한 값의 비율이다.

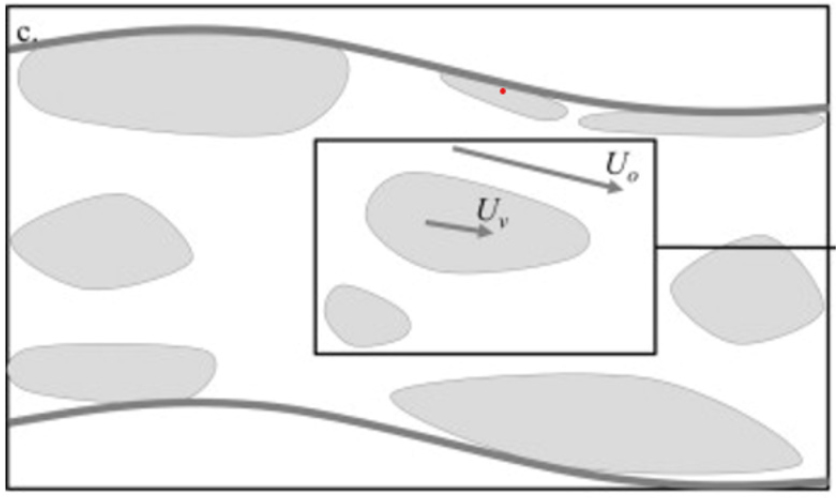
Fig. 4.

Schematic view of patches (in grey) and flow velocities in a reach (excerpted from Luhar and Nepf, 2013; Fig. 1c)

Walter et al. (2024)은 정수 조건에서 LAI 기반 모형 중 Järvelä (2004), Västilä and Järvelä (2014), Folke et al. (2019)의 세 모형을 그들이 실험실에서 직접 측정한 마찰계수 값들과 비교, 평가하여 Västilä and Järvelä (2014) 모형이 상대적으로 우수하다고 하였다. 나아가, 이 모형은 잎과 줄기가 흐름저항에 미치는 영향을 구분하여 고려하였기 때문에 계절에 따라 변하는 홍수터 혼합식생에 대한 마찰계수를 예측하는 데 적합하다고 하였다. Walter et al. (2024)은 정수 조건에 적용된 LAI 접근방법을 침수조건에 확대적용 하였다. 그들의 모형에서 침수조건에서 식생의 휨 높이(deflection height)를 정확히 산정하는 것이 중요함을 강조하였다.

정수 조건에서 유연한 식생군, 즉 패치형태 및 패치군으로 이루어진 구간 규모에서 식생흐름저항에 대한 실험적 연구는 최근에 국내에서 활발히 수행되었다. Ji et al. (2023)은 정수 조건에서 버드나무와 같은 거의 실물과 같이 만든 목본류를 다수의 패치 형태로 실규모 수로에 설치하고 실험유량 1.5~ 2.8 m³/s, 유속 0.3~0.7 m/s, 수심 약 1.0 m에서 구간 규모에 대한 마찰계수를 구하였다. 그들의 실험은 모형식생의 물리적 특성의 유사성과 흐름 규모 측면에서 기존의 연구와 비교하여 독보적이다. 그 결과, 부피 차폐계수가 단지 4~10% 수준에서 식생밀도 및 차폐계수에 따라 식생 마찰계수는 1.7~5.5배로 커지는 것을 확인하였다. 그들이 사용한 차폐계수는 수로 단면을 기준으로 한 것이 아니라 수로 평면을 기준으로 얻어진 것으로서, 불규칙한 패치로 이루어진 구간 규모의 마찰계수 평가에 상대적으로 유리하다. 그들은 나아가 Järvelä (2004), Västilä and Järvelä (2014), Baptist et al. (2007), 그리고 Luhar and Nepf (2013) 모형을 대상으로 그들이 얻은 실측치와 비교, 검토하였다. 그 결과 처음 두 모형은 흐름에 의한 식생의 재배열 효과를 고려할 수 있으므로 그들이 수행한 실험 규모 이상의 흐름에서 유리한 입장이고, 줄기면적 대비 잎 면적 비율이 적은 경우 적절함을 보인다고 하였다. 후자 두 모형도 항력계수나 기타 매개변수의 적절한 선택이 가능한 경우 실규모 실험 결과와 유사한 값의 결과가 나타난다고 하였다.

또 다른 실험연구로서 Bae et al. (2024)은 패치군으로 이루어진 구간 규모의 식생 흐름저항에 미치는 요인으로 식생밀도, 단면적과 평면 차폐면적 등을 이용한 패치의 기하형태, 부피로 계산된 차폐계수, 그리고 한 하천단면에서 패치의 위치 등을 인자화(parameterization) 하였다. 그들은 Ji et al. (2023)의 연구에서 얻어진 실험자료에 식생의 LAI를 2배로 증가시킨 조건에서 얻어진 실험결과를 추가하여 정수 조건의 유연한 식생 실험에서 얻어진 마찰계수를 하나의 경험공식으로 표시하였다. 그 결과 마찰계수는 식생밀도가 크고 차폐계수가 비교적 적은 경우 사실상 차폐계수에 관계하고, 그 다음 식생밀도에 관계하는 것으로 나타났다. 마지막으로 하도 내 패치의 위치가 중앙에서 강턱 방향으로 옮겨가는 경우 흐름장이 바뀌어 마찰계수 역시 변하는 것을 확인하였다.

2.2.4 침수, 유연한 식생(Submerged, flexible vegetation)

실제 유연한 식생, 특히 초본류는 물에 완전히 잠긴 경우가 많으므로 단단한 식생과 달리 완전히 침수된 유연한 식생이 주요 대상이다. 이를 도식적으로 표시하면 Fig. 5와 같다. 이 그림에서 hvf는 흐름에 의해 재구성(reconfiguration) 된 식생의 높이이다. 이 경우 실제 식생은 같은 흐름조건에서도 불안정하게 위아래로 흔들리기 때문에 그에 따라 식생높이도 달라진다. 유연한 식생모형은 식생자체가 흐름에 의해 휘기 때문에 흐름과 식생저항 간에는 상호작용이 있어 단단한 식생모형에 비해 현상이 복잡하다(Kouwen and Li, 1980). 흐름에 의해 갈대, 달뿌리풀 같은 대형 초본류가 뉘이게 되면 같은 조건에서 단단한 식생에 비해 흐름저항이 대폭 감소한다(Rhee et al., 2008). 잎과 유연한 가지가 많은 목본류도 특히 흐름에 따라 유선형으로 변하면서 흐름저항은 줄어든다(Freeman et al., 2000). 이에 해당하는 대표적인 식생은 우리나라에 지배적인 수변식생인 버드나무류 중 목본성 버드나무이다.

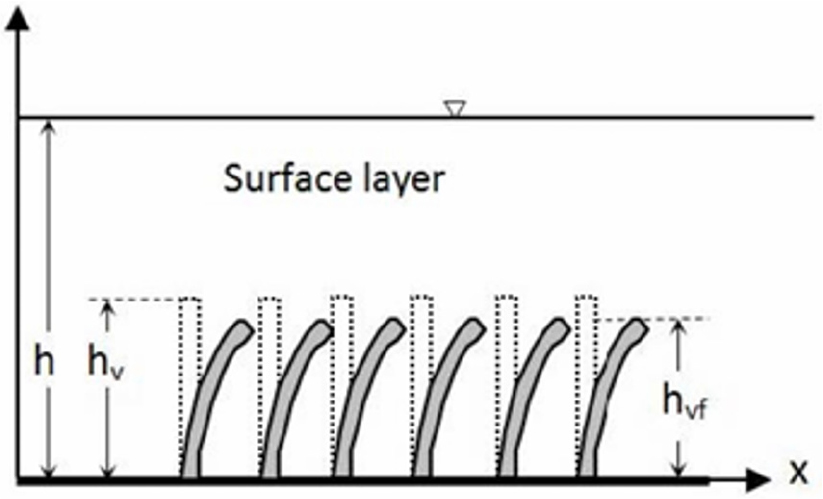
Fig. 5.

Schematic diagram of submerged flexible vegetation (hvf: bended vegetation height)(Excerpted from D’Ippolito et al., 2021; Fig. 7)

이 분야 최초 연구는 1940년대 미국에서 식생이 자라는 관개수로 설계를 위해 실험실 자료를 이용한 Palmer (1945)의 연구이다. 그 후 초본성 식생이 자라는 관개수로의 조도계수 문제는 지속적인 연구와 실험으로 1980년대에 식생상태를 세분화한 여러 경험식들이 소개되었다(Gwinn and Ree, 1980). 이 분야 연구는 대부분 실험실 자료를 이용하여 매닝계수나 마찰속도 u*를 관련 인자 간 경험식으로 나타냈다.

위와 같은 경험식에서 벗어나 침수된 유연한 식생에 관한 해석적 접근은 1980년대 들어 시작하였다. Kouwen et al. (1981)은 식생의 영향을 유속의 연직분포에 관한 기존 대수식에 반영하였다. 그들의 식에는 이른바 MEI라는 굴곡탄성률을 이용하여 한계마찰속도를 구하고 이를 이용하여 V/u*로 표시되는 대수 유속분포식의 경험계수를 구하게 하였다. 이와 같은 준 이론적 방법론은 그 후 당시로는 대규모 실험수로에서 초본/목본류의 인공/자연 식생을 이용하여 실험을 통해 보완되었다(Järvelä, 2002).

Kouwen et al. (1981) 연구 이후 식생의 생물역학적 특성을 고려하기 위해 Freeman et al. (2000)은 강성계수 E, Kouwen and Fathi-Moghadam (2000)은 식생지수 ξE, Whittaker et al. (2015) 등은 휨강성 EI 등을 제안하였다(Lee and Rhee, 2023). 여기서 강성계수 E는 탄성계수라고도 하며 재료(이 경우 식생줄기)의 변형에 대한 저항정도를 나타내며, 휨강성 EI는 재료의 휨에 대한 저항정도를 나타내며, 강성계수 E에 재료의 단면2차모멘트 I를 곱한 값으로 나타낸다. 식생지수 ξE는 한 식생의 자연적 공명주기, 총질량, 높이 등에 관련된 값으로써, 한 수종에 대해 모두 같다.

마지막으로, Li et al. (2014)은 3D ADV (Acoustic Dopppler Velocimeter)를 이용하여 침수된 유연한 인공식생이 유속, 레이놀즈 전단응력, 난류강도 및 매닝계수 등에 미치는 영향에 대해 연구하였다. 그들은 실험결과를 기반으로 식생밀도와 유량에 따른 유속분포와 매닝계수 등의 방정식을 제시하였다. 이들의 실험에서 유속분포는 상부 비식생층, 중간층, 하부층인 세 층으로 나누었다.

지금까지 소개한 해석적 식생 흐름모형에서 침수/정수, 단단한/유연한 식생 등 모든 조건에서 공히 처음에 시작하는 접근법은 흐름방향의 운동량방정식에 식생에 의한 저항을 추가하는 것이다. 일차적으로 연구자들은 식생을 단순히 홍수터에 균일하게 분포하는 원통형 강체로 가정하였으며(Baptist et al., 2007; Cheng, 2011; Stone and Shen, 2002; Tanino and Nepf, 2008), 이는 잎과 가지가 나무 몸통에 비해 상대적으로 작은 목본류에는 합리적인 가정이다(Wang and Zhang, 2019). 특히 부분 침수된 목본류의 경우가 이에 해당한다. Järvelä (2004)는 잎이 없는 나무 몸통과 가지의 전면부 면적을 추정하기 위하여 하천차수기법의 적용성도 검토하였다. Whittaker et al. (2015)은 실제로 측정된 투영면적을 이용할 것을 제안하였다.

그러나 실제 하천에서 잎이 있는 식생 하나하나의 투영면적 자료를 도출하는 것은 사실상 비현실적인 것으로서, 그 대신 제안된 지표가 이른바 잎면적지수(Leaf Area Index, LAI)이다(Järvelä, 2004; Jalonen et al., 2012). 흐름 속 식생은 줄기는 휘고, 잎은 모두 유선방향으로 재배열(reconfiguration) 되어 투영면적이 대폭 줄어든다. 이러한 현상을 고려하기 위해 Järvelä (2004), Whittaker et al. (2015)는 식생의 Cauchy 수를 고려하여 유속에 대한 식생의 재구성 매개변수인Vogel 지수(Vogel, 1994; De Langre, 2008)를 항력식에 도입하였다. 식생의 Cauchy 수는 유연한 잎과 가지가 흐름에 의해 재배열되는 정도를 나타내는 척도이며, Vogel 지수는 유속에 의해 이러한 재배열이 일어나는 정도를 나타낸다.

지금까지 수십년에 걸쳐 해석적, 실험적 방법으로 식생에 의한 흐름저항을 평가하는 모형 개발에 많은 노력을 기울였음에도 불구하고 아직 이론적 해석모형이나 실험실 실험결과를 실제 현장규모로 확대하는 것은 여전히 불확실성이 있다(Albayrak et al., 2014). 즉, 실제 식생하천에서 식생패치 형태의 다양성과 식생자체가 흐름에 의해 그 형태가 바뀌는 재구성 효과 등으로 인해 소규모 과정을 단순히 통합하여 해석할 수 있는 문제는 아니기 때문이다(Ji et al., 2021).

2.3 조도계수 공식

전 절에서 해석적 방법으로 식생하천의 흐름저항 특성을 넷으로 나누어 기존 연구성과를 정리하였다. 그러나 이러한 연구성과를 하천실무에 이용하게 위해서는 식생 흐름저항을 대표하는 계수 f나 n 값으로 나타내야 간단한 1차원 등류모형인 매닝 공식부터 시작하여 기존 흐름모형에 이용할 수 있다.

Wang and Zhang (2019)는 실무에서 세계적으로 널리 쓰이는 1차원 HEC-RAS (Hydrologic Engineering Center-River Analysis System)에 적용할 수 있는 식생하천의 매닝계수 공식들을 비교 평가하였다. 그들이 평가한 공식들은 Freeman et al. (2000), Whittaker et al. (2015), Järvelä (2004) 공식 등 총 11개(원전의 Table 1)이며, 평가에 이용된 하천은 조밀하고 다양한 식생이 있는San Joaquin River 구역이다. 이 구역의 주요식생은 포플러, 버드나무 등 목본류, 관목, 초본류, 갈대 등이며, 평가에 쓰인 최대유량은 200 m³/s, 매닝계수는 평균 0.05~ 0.14 범위이다. 그 결과Freeman et al. (2000) 공식은 그 개발에 이용된 실험수로 깊이 1.5 m를 초과하는 흐름에 대해서는 확실히 매닝계수를 과다평가 하고, 유연한 식생에 대해 차폐효과를 고려한 Whittaker et al. (2015) 공식은 하천수위를 다른 공식들에 비해 대체적으로 잘 예측하는 것으로 나타났다.

2.4 수치해석

고체 경계면 마찰이건, 유체 간 마찰이건 난류가 발생하면 난류마찰(레이놀즈 응력)과 와류에 의한 항력이 발생한다. 자연하천 이든 인공수로 이든 개수로 흐름은 대부분 난류이다. 따라서 식생에 의한 흐름저항을 평가하는 방법 중 근본적인 것은 난류를 해석하는 것이다. 현재 난류해석은 실험을 제외하고는 CFD (Computational Fluid Dynamics) 수치모형에 의존한다. 식생이 있는 흐름을 해석적으로 접근하는 데에는 근본적으로 항력계수와 레이놀즈 응력이라는 두 가지 불확실성이 존재한다. 이러한 한계를 극복할 수 있는 방법으로 CFD를 활용한 난류 수치해석이 제안되었다(Nepf, 1999; Rodi, 2017). 식생흐름을 모의하기 위해 난류 수치해석은 수로에 원통형 막대를 서로 다른 밀도로 배치한 흐름을 분석하는 것부터 시작하였다.

난류 수치해석에는 크게 RANS (Reynolds-averaged Navier Stokes equation) 모형, LES (Large Eddy Simulation) 모형, DNS (Direct Numerical Simulation) 등이 있다. 이 세 모형 중 RANS는 시간평균 한 Navier-Stokes 방정식 모형으로서, 난류성분은 적절한 난류모형으로 대체된다. 이 모형은 난류의 시간평균 된 값을 얻을 수 있으며(Shimizu and Tsujimoto, 1994), 위 세 모형 중 가장 먼저 개발되었다. 이 모형은 식생에 의한 항력을 운동량방정식에 추가하고, 식생관련 난류성분에 의한 난류 생성과 소산을 설명하는 항력 관련 항을 난류모형의 이송방정식에 고려한다. 이에 따른 두 경험계수(항력계수와 난류관련계수)의 선정이 모형결과에 중요하게 된다. Wilson et al. (2006)은 흐름에 잠긴 잎이 없는 단단한 식생의 경우 항력계수가 단면 유속분포 등 흐름 및 저항 특성에 큰 영향을 주지만, 유연한 식생의 경우 흐름에 식생이 굽혀지는 정도가 더 큰 영향을 준다고 하였다.

LES 모형은 RANS 모형과 비교하여 대규모 와류를 직접 계산할 수 있다는 점에서 항력계수나 레이놀즈 응력과 같은 경험적 계수에 상대적으로 덜 의존한다. 다만, LES에서도 소규모 와류는 SGS (Sub-Grid Scale) 모델링을 통해 처리되므로 소규모 난류의 정확한 추정은 여전히 필요하다. LES 모형은 저해상도 격자를 사용할 수 있고 경험적 항력계수에 대한 사전 지식 의존도가 낮아 대규모 난류 구조의 모의에 유리하다.

2000년대 중반 Stoesser et al. (2006)은 LES를 식생 밀도가 높은 흐름 환경에서 적용하였으며, 이후 Stoesser et al. (2010)은 수로에 원통형 막대를 배치하여 항력계수를 산정하고 실험실 관측자료와 비교적 잘 맞는 것을 확인했다. Kim and Stoesser (2011)는 그 동안 RANS와 LES 모형을 적용한 총 12개의 식생흐름저항 CFD 연구를 하나의 표(원전의 Table 1)로 정리하였다. 반면에 DNS 모형은 난류부정류를 직접 계산하기 때문에 RANS 보다 높은 정확도를 보이지만 계산 시간과 비용이 매우 많이 든다(Kim and Stoesser, 2011).

이와 같은 난류 수치해석을 통한 접근법에는 다음의 본질적인 한계가 있다. 첫째 실무에서 많이 쓰이는 RANS 모형은 난류는 매우 복잡하고 비선형적인 흐름임에도 불구하고 평균 흐름만 해석한다. 이에 따라 소규모 난류나 대규모 와류의 상호작용을 정확히 반영하기 어렵기 때문에 흐름의 정확한 예측이 어렵다. 두번째, 난류의 비선형성으로 인해 지형이 복잡할수록 해결해야 할 격자 수가 매우 많아진다. 무엇보다도 난류 해석에서 중요한 경계층을 정확히 모의하는 것이 어렵다. 특히 식생이나 장애물이 있는 흐름에서 경계층 변화를 정밀하게 예측하는 데 한계가 있다. 또한, 난류의 초기 조건과 경계 조건에 매우 민감하여, 이에 따라 해석 결과의 신뢰성이 감소할 수 있다. 이에 따라 고해상도 LES나 DNS과 같은 고급 난류 모의기법은 계산비용이 매우 커지고, 실시간 모의가 어려워 실용성이 제한된다. 이러한 한계로 난류 수치해석을 통한 접근법은 여전히 흐름저항에 대한 완벽한 해답을 제공하지 못한다. RANS는 실험자료를 기반으로 모형의 정확성을 검증하는 과정이 중요한데, 실험 비용과 시간이 제한되므로 Kim and Stoesser (2011)는 LES 모형으로 식생 항력계수를 산정하여 전체 RANS 결과의 정확도를 높이는 방법을 제안하였다. 즉, 식생 군락이나 패치가 있는 홍수터의 거시적 흐름저항을 연구 시, 미시적 관점의 식생밀도에 따른 항력계수 CD는 LES 모형으로 산정하고, 그 결과를 식생패치를 포함한 홍수터 전체 RANS 모델에 적용하여 결과의 정확도를 높이는 추가적인 연구를 수행하는 것을 고려해 볼 수 있다.

3. 국내의 연구연혁

국내에서 하천식생에 의한 흐름저항 관련 기술은 근대식 하천사업(주로 하천개수사업)이 확대되기 시작한 1960년대 이후 학계, 실무 공히 매닝계수를 경험적으로 추정하거나 보정하여 사용하는 수준에 머물렀다. 그 당시만 해도 하천식생의 번무 정도가 지금 수준에 비해 상대적으로 적었기 때문에(Woo and Park, 2016) 하천식생에 의한 추가적인 흐름저항 문제는 관심이 덜 했을 것이다. 그러나 1970-90년대 댐건설사업의 확대, 80년대 이후 비점오염물질의 하천 이입, 그후 기후변화 등의 이유로 국내 대부분의 하천에 식생이입이 가속되어 초본류, 목본류 등의 식생으로 덮여 있다(Kim and Kim, 2019). 이러한 현상을 화이트리버의 그린리버 화(化)라 부르기도 한다(Woo, 2008). 이에 따라 식생에 의한 흐름저항은 하천수리 실무에서 중요한 문제로 떠오르고 있다.

국내에서 하천식생 흐름저항 관련 연구는 사실상 2000년대 들어와서 본격적으로 시작되었다. 그 이유는 70-80년대 댐건설과, 특히 2000년대 들어 기후변화 등의 이유로 국내하천에 많은 식생이 이입, 활착하게 되었고 그로 인해 홍수피해가 발생함에 따라 실무요구가 커졌기 때문이다. 특히 홍수위 상승에 큰 영향을 주는 목본성이나 목본/초본이 혼재한 식생군락의 흐름저항계수를 명확히 추정하는 모형이 필요하게 되었기 때문이다. 10년 사이에 활발하게 진행되었다

이 분야 국내 연구로 Rhee et al. (2006)은 한국산 잔디와 양잔디(Perennial Ryegrass)에 대해 완전 침수상태에서 수로실험을 수행하였으며, 이를 통해 유량이 증가하면 매닝계수는 한국산 잔디의 경우 0.03, 양잔디의 경우 0.06로 수렴하는 것으로 나타났다. 나아가 Rhee et al. (2008)은 Zoysia matrella (한국산 잔디), Pennisetum alopecuroides (L.) Spreng. (수크령), Phragmites communis Trin. (한국산 갈대) 등을 대상으로 실험수로에서 식생에 의한 매닝계수를 산정하였다. Rhee et al. (2012)은 다시 국내하천에 가장 흔한 초본류인 갈대, 달뿌리풀, 물억새 등을 대상으로 실험실 수로에서 조도계수를 측정하여 이를 VR 값과 상관시키고 그 결과를 조도계수 산정 가이드라인으로 이용하게 하였다. 위 식생에 의한 조도계수 변화는 VR이라는 수리량 이외에 식생의 강성(E), 성장시기(녹색 성장기, 갈색 휴면기 등) 별로 조도계수 값이 달라지기 때문에 일관된 가이드라인을 제시하는 것은 어렵지만 VR 값이 충분히 클 경우 조도계수는 갈대 0.014, 달뿌리풀 0.018, 물억새 0.012 정도로 수렴하는 것으로 나타났다. 이 결과는 국내 하천에서 초본류의 경우 위 세 종이 대부분이고, 홍수는 보통 식물생장이 왕성한 여름 전후이기 때문에 실무적인 면에서 귀중하다.

다음 2010년대 초 국내에서 비교적 활발히 연구했던 분야는 기존, 또는 일부 수정된 1, 2차 수치모형에 수목에 의한 항력 항을 추가하고 식생하천에 적용하는 것이다. 이는 특히 홍수터 식재라는 사회적 이슈가 대두되면서 하천전문가들의 관심을 촉발하였다. Kim et al. (2010)은 국내 처음으로 식생에 의한 항력 항이 포함된 수심평균 2차원 수치모형을 개발하였다. 식생은 ‘단단한’ 원주형으로 가정하고 식생항력식을 유도하여 흐름 운동량방정식에 추가하였다. Kim et al. (2011)은 기존의 FESWMS 이차원 흐름모형에서 교각에 의한 항력을 수목에 의한 항력으로 대체하여 홍수터 일부에 하안림을 조성하는 경우 나타나는 수위 및 유속 변화를 검토하였다. 그 결과 식생에 의한 흐름저항을 고려하기 위해 운동량방정식에 식생항력 항을 고려하는 것과 에너지방정식에 매닝계수를 조정하여 수치해석 하는 것이 수위상승에서 서로 비슷하게 나타났으나 유속은 후자가 전자에 비해 작게 나타났다. 따라서 매닝계수를 조정하여 식생 흐름저항 효과를 모의하는 접근법은 홍수 시 수목의 전도가능성을 과소평가할 수 있다

마지막으로 Kim et al. (2009)은 국내 총 44개 식생하천을 포함한 일반하천에서 조도계수 현장자료를 수집하여 분석하였다. 그들은 그 결과를 자료수집 지점별로 사진자료를 포함하여 유량에 따른 매닝계수의 변화를 그림으로 제시하였다. 이 자료는 식생 이외에 흐름저항에 영향을 주는 하상재료, 하천형태, 만곡 등의 영향이 섞여 있지만 유사한 하천여건에서 참고자료로 이용될 수 있을 것이다.

Ji et al. (2021)은 2차원 흐름모형을 하천에 적용하기 위해 홍수터 식생의 물리적 특성과 분포 특성을 고려하여 Baptist (2005) 모형을 이용하여 조도계수를 산정하였다. 이를 위해 지상라이다를이용한 식생의 3차원 포인트 클라우드 분석을 수행하였으며, 홍수터 식생분포는 국부적으로 식생이 존재하는 경우와 홍수터 전체에 식생이 분포하는 경우로 구분하여 모의를 수행하였다. 이러한 과정은 조도계수 공식을 실제 국내 식생하천에 적용하는 경우 반드시 필요한 자료 수집, 처리 절차로서, 이는 2차원 흐름모형 뿐만 아니라 앞서 소개한 Wang and Zhang (2019) 1차원 흐름모형 적용시에도 필요하다.

기존의 하천흐름모형 적용시 식생에 의한 추가적인 흐름저항을 고려하기 위하여 마찰계수 f나 조도계수 n 값을 보정하는 공식을 사용할 수 있다. 이러한 공식들의 비교 평가에 대해서는 2.2절에서 소개하였다. 국내연구에서도 해외와 비슷한 수준의 비교평가 연구가 Lee and Rhee (2023)에 의해 진행되었다. 이들은 Freeman et al. (2000) 공식 등 8개 공식에 대해 실무 수리계산의 관점에서 각 공식의 특성과 적용성을 비교 평가하였다. 이를 위해 각 공식의 수심 별 산정결과를 비교하고, 수관부 영향, 수목밀도와 직경 영향, 수목 강성계수 영향, 수위산정 결과 등을 분석하였다. 그 결과 Kouwen and Fathi- Moghadam (2000) 공식 등은 조도계수를 타 공식에 비해 과도하게 산정하는 것으로 나타났다. 식생 강성계수를 고려하는 Freeman et al. (2000) 공식과 Whittaker et al. (2015) 공식은 강성계수에 따라 조도계수가 매우 큰 차이를 나타냈다. 각 공식으로 계산된 조도계수를 국내 중소규모 가상하천에 적용한 결과 공식 별 약 0.2~0.4 m 정도의 수위차를 보였다. 그들은 결론적으로 입력자료의 불확실성이 낮은 Baptist et al. (2007), Huthoff et al. (2007), Cheng (2011), Luhar and Nepf (2013) 등의 4개 공식이 국내 실무적용에 상대적으로 적합하다고 판단하였다.

마지막으로, Lee et al. (2023)은 비교적 신뢰도가 높은 조도계수 공식으로 알려진 Freeman et al. (2000) 식을 이용하여 가상하천에 대해 HEC-RAS 모형을 적용하여 유량과 수위 변화에 따른 매닝계수의 변화를 확인하였다. 그 결과 수위가 식생의 높이에 도달할 때까지 조도계수가 지속적으로 증가하다 수위가 식생높이를 초과하여 높아지면 지속적으로 감소하는 것으로 나타났다. 이 결과는 식생에 의한 흐름저항은 단지 식생의 존재뿐만 아니라 수위(유량)와도 관련성이 있다는 것이며, 기존의 해외연구에서 잘 알려져 있다.

4. 연구수준 및 국내적용성 검토

1950년대 이후 문헌에 나타난 하천식생의 흐름저항 관련 국내외 연구는 총설 성격의 논문으로서 D’Ippolito et al. (2021)이 사실상 유일하며, 그 상위분야 총설논문에서 식생 흐름저항을 한 부분으로 다룬 논문들이 몇 있다. 그 밖에 식생 흐름저항 관련 단일 주제를 다룬 논문은 수백 편 보인다. 이러한 논문을 검토하여 평가된 연구수준은 다음과 같다.

4.1 제 방법의 수준검토

4.1.1 도표식 방법

이 방법은 국제적으로 1940년대부터 개발된 이후 1950-60년대 완성된 것으로서, 적용이 비교적 간단 하지만 경험에 의존한다. 이 방법은 대체할 신뢰도 높은 대안의 부재로 지금도 국내외 실무에서 통용되고 있다. HEC-RAS와 같이 세계적으로 통용되는 대표적인 하천흐름 모형에서도 하천 식생상황을 경험적 매닝계수로 바꾸어 사용하고 있다. 국내 하천은 과거와 달리 식생이입으로 흐름저항이 대폭 증가하였음에도 불구하고 하천설계기준의 하도계획 편에 조도계수는 여전히 경험적으로 결정하거나 하상재료를 조사하여 결정하도록 주문하고 있다(KWRA, 2019).

4.1.2 해석적 방법

식생 흐름저항을 해석적으로 접근하는 방법은 대부분 흐름의 한 지배체적에서 식생에 의한 항력을 추가한 운동량방정식에 Eq. (1)을 고려하여 마찰계수나 조도계수를 유도한다. 이 방법을 적용하는데 가장 간단한 대상은 주로 교목과 같은 단단한 식생이 물 위로 나와 있는 경우이다. 그 다음이 단단한 식생이 물속에 잠긴 경우이다. 이 조건에 많이 쓰이는 흐름 모형은 위층은 대수분포, 아래층은 식생에 의한 균일분포 같은 이른바 이층 모형이다. 유연한 식생으로 가면 정수, 침수 모두 접근하기 어렵지만 그래도 정수 조건이 상대적으로 용이하다.

본 연구에서 수집한 기존의 해석적 흐름저항 모형에 대한 평가 연구는 Wang and Zhang (2919), Lee and Rhee (2023), Ji et al. (2023), Walter et al. (2024) 등으로서, 이 결과를 토대로 하나의 표로 정리하면 다음 Table 1과 같다. 이 표에서 추천된 모형(공식)들은 지금까지 국내외 문헌분석을 통해 확인된 평가결과에 기초한 것이며, 이 연구에서 별도 수행된 결과가 아니므로, 객관성은 한계가 있다.

한편, 실무 측면에서 식생 하나에 의한 흐름저항 효과는 사실상 관심 대상이 아니다. 실무에서는 1) 단일, 또는 유사 수종이 매트릭스 같이 균일 분포하는 경우와 2) 복수의 서로 다른 패치가 불규칙하게 분포하는 경우가 중요하다. 이는 기존의 흐름 수치모형을 적용할 때 특히 중요하다.

4.2 국내 식생하천의 일반적 특성 및 흐름저항계수 공식의 적용성

국내 중소하천은 주로 초본류가 매트릭스를 이루며 중간 중간에 목본류가 패치 형태로 있다. 그러나 대하천은 초본류와 목본류 매트릭스가 공존한다. 초본류로서 갈대, 달뿌리풀이 대부분이며, 일부 수크령, 사초류 등이 있다 (Woo et al., 2022). Fig. 6은 국내 대표적인 초본류 하천을 보여준다. 이 경우 조도계수는 Rhee et al. (2012)의 실험치를 상한치로 하여 기존 도표식 방법을 참조하여 결정할 수 있을 것이다.

Fig. 6.

A stream filled fully with grass (reeds)(Pocheon-cheon Stream, Gyeonggi-do, Korea)(photo from Pocheon City)

목본류의 경우 대부분 관목성/교목성 버드나무류로 되어 있으며(Kim et al., 2014), 홍수관리 차원에서 우선적으로 중요하다. Fig. 7은 국내 대표적인 패치형태의 목본류 하천을 보여준다.

Fig. 7.

A typical vegetative (woody) river reach in Korea (Naesung- cheon Stream in Gyeongsangbuk-do Province, Korea)(Excerpted from Fig. 1; Bae et al., 2024)

이러한 형태의 식생하천에 대해서는 기존 식생흐름 모형에 항력식을 추가하고, 적절한 항력계수를 채택하여 수치해석으로 흐름특성을 구할 수 있을 것이다. 그러나 그보다 더 실용적인 방법은 식생저항 효과를 해석적인 방법으로 마찰계수, 매닝계수, Chezy 계수로 환산, 제시하는 공식들을 직접 이용하는 것이다. 다양한 조건 별로 검토할 수 있는 공식들을 Table 1에 정리하였다. 여기서 강조될 것은 식생에 의한 흐름저항을 하상의 거친 정도에 추가하여 ‘통(lump)’으로 푸는 방법과 식생 항력식을 운동량방정식에 추가하여 관련 방정식을 푸는 방법 간 차이다. 전자는 주로 Table 1과 같은 해석적 방법에 쓰이는 것으로서, 식생흐름저항이 고려된 마찰계수나 조도계수로 나타난다. 후자는 주로 수치해석에 쓰이는 방법으로서 논리적으로 우월하다. 두 방법은 수위계산에서 큰 차이가 없으나, 전자는 연직 유속분포나 그에 따른 세굴과 퇴적 등 추가적인 현상을 모의하는 데 한계가 있다.

마지막으로, 국내하천에 단일, 또는 유사종의 식생이 매트릭스 형태로 널리 분포하는 경우도 일부 있지만 Fig. 7과 같이 패치 형태의 식생이 하천에 불규칙하게 분포하는 경우가 많으므로 이에 대한 접근은 Luhar and Nepf (2013), Bae et al. (2024) 방법과 같이 패치 규모(patch scale)나 구간 규모(reach scale) 접근법이 바람직하다.

5. 요약 및 결론

식생흐름저항 관련 해외 연구를 분석한 결과 1) 단단한/유연한 식생형태, 2) 침수/정수 등 식생과 수면의 상대적 위치, 3) 수위 상승 시만 침수되는 홍수터 식생과 상시 침수되는 하도 수생식생 등 하천 내 식생의 위치, 4) 단일식생, 패치, 하천구간 등 흐름저항 대상 식생군의 형태 등으로 구분하여 접근하였다.

구체적으로 1940-50년대에 일부 초본류 수로실험을 통해 조도계수를 검토하는 방법부터 시작하여, 식생상황을 정성적으로 기술하거나 관련 사진을 제시하고 그에 맞는 조도계수를 채택하는 방법 등이 제시되었다.

1970년대 이후부터 단단한 식생에 의한 해석적 흐름모형이 개발되기 시작하여 항력계수 식에 줄기의 밀도/직경 등 식생의 물리적 특성이 반영되기 시작하였다. 이러한 모형은 제한된 조건에만 적용 가능하며, 흐름에 의한 식생변형의 고려는 불가하고 실제 사용시 모형의 보정이 필요하다. 1980년대 이후에는 항력계수와 줄기의 밀도, 생물기계적 특성 등을 이용한 유연한 식생모형이 개발되기 시작하여 식생배치까지 고려되었다. 나아가 2010년대부터 식생 하나 하나에 의한 흐름저항 평가를 넘어 식생군에 의해 형성되는 패치에 의한 저항을 평가함으로써 하천구간 규모에서 흐름저항을 평가하는 방향으로 나가고 있다. 이러한 방법은 흐름 및 식생 조건에 따라 적절한 흐름저항계수(마찰계수 또는 조도계수) 공식을 선정하여 직접 적용하거나, 기존 흐름모형에 식생항력 항을 추가하고 적절한 항력계수 공식을 이용할 수 있다.

수치해석 방법은 각각의 방법이 가지는 본질적인 한계를 극복하고 실무에 안정적으로 이용할 수 있는 기법이 아직 가용하지 않다.

국내 식생하천은 초본류로서 갈대, 달풀이풀이 대부분이며, 일부 수크령, 사초류가 있다. 이 경우 조도계수는 Rhee et al. (2012) 연구성과를 상한치로 하여 기존자료를 참조하여 결정할 수 있을 것이다. 목본류의 경우 대부분 관목성/교목성 버드나무류로 되어 있으며 홍수관리 차원에서 우선적으로 중요하다. 국내 식생하천의 특성상 하천식생 흐름저항 연구는 특히 버드나무류가 흐름에 겨우 잠기거나 위로 나온 조건에서 실무에 바로 쓸 수 있는 성과가 요구된다. 이러한 연구는 실물실험을 통한 검증이 바람직하다.

국내하천에 단일, 또는 유사종의 식생이 매트릭스(바탕) 형태로 널리 분포하는 경우도 일부 있지만 대부분 패치(조각) 형태의 식생이 하천에 불규칙하게 분포하는 경우가 많으므로 이에 대한 접근은 Luhar and Nepf (2013)나 Bae et al. (2024) 방법과 같이 패치 규모나 구간 규모 접근법이 바람직하다. 식생패치 분포의 불규칙성과 패치 내 식생 종의 이질적 분포(초본과 목본류가 함께 존재), 홍수터 위 식생패치가 존재하는 경우와 사주에 식생이 덮여 형성된 식생사주 경우 등 다양한 현장 조건과 자연하천의 복잡성을 고려한 추가적, 지속적 연구가 필요하다.

마지막으로, 해석적 방법으로 흐름저항계수를 산정하고자 하는 경우 국내외 문헌분석을 통해 확인된 평가결과에 기초한 Table 1을 참조할 수 있을 것이다.