1. 서 론
2. 자료 및 연구방법
2.1 자료
2.2 식생지수
2.3 가뭄지수
2.4 SPI와 nEDDI를 VHI와 코퓰러 결합한 생태학적 가뭄모형
3. 결 과
3.1 가뭄지수의 시간 척도 결정
3.2 코퓰러 기반 접근방법의 예시 결과
3.3 VHI와 SPI 사이의 의존성의 공간적인 패턴
3.4 VHI와 nEDDI 사이의 의존성의 공간적인 패턴
4. 산림 식생의 생태학적 가뭄에 미치는 강수와 잠재증발산의 상대적인 중요도
5. 결 론
1. 서 론
기후는 식생의 장기적인 동역학과 광범위한 분포를 제어한다. 반대로 식생은 에너지, 물, 기타 생물리학적 프로세스에 영향을 줌으로써 기후를 조절하기도 한다(Pielke et al., 1998; Friedlingstein et al., 2006; Peng et al., 2014; Zhou et al., 2014; Piao et al., 2015). 따라서 기후에 대한 식생의 반응을 조사하는 것은 육상 생태계의 동역학을 이해하는 데 중요하다(Knapp and Smith, 2001; Lévesque et al., 2013). 지난 수십 년 동안 NDVI (Normalized Difference Vegetation Index)는 육상 식생 생산성의 대리 지표로 광범위하게 사용되었으며 기후변화에 대한 식생 반응을 탐지하는 데 널리 적용되었다(Ichii et al., 2002; Tourre et al., 2008; de Jong et al., 2012; Duan and Bastriaanssen, 2013). 또한, NDVI는 식생 표면에 대한 시간적, 공간적 연속적인 정보를 제공하므로 식생 관련 가뭄 모니터링 및 영향 평가에 사용될 수 있다(Asner and Alencar, 2010; AghaKouchak et al., 2015). 농업, 기상, 수문학적 지수를 포함한 기존의 지상 관측자료 기반의 가뭄지수와 비교하여 위성 기반 식생 관측자료는 가뭄이 생태계에 미치는 영향을 평가할 수 있게 하며 전 세계적인 공간 영역에서 일관된 시공간적인 해상도로 거의 실시간에 가까운 가뭄지수를 생성할 수 있게 한다(Heumann, 2011). 가장 빈번하게 사용되는 식생지수인 NDVI (또는 파생제품)는 식생 관련 가뭄의 정량적 모니터링 및 평가에 널리 사용되었다(Ji and Peters, 2003).
다양한 자료와 통계적 접근 방식을 기반으로 다양한 지역에서 식생과 기후변수 사이의 연관성을 조사한 여러 연구가 있다(Li et al., 2002; Piao et al., 2010; Zhong et al., 2010; Peng et al., 2011; Cong et al., 2013; Zhang et al., 2013; Piao et al., 2014; Won et al., 2020b). 그러나, 결합 확률 의존성에 기반한 관점에서 식생 관련 가뭄의 가능성과 대기의 수분공급 및 수요 조건에 대한 민감도를 확인하기 위한 연구는 여전히 부족하다. 이러한 확률론적 식별은 기후 변동성에 대한 식생 반응을 이해하는 데 중요한 통찰력을 제공할 수 있다(Liu et al., 2016).
본 연구의 목표는 위성 원격 감지 관측자료를 사용하여 우리나라 전역의 산림 식생 관련 가뭄의 가능성을 조사하는 것이다. 본 연구에서는 먼저 기상청 ASOS (Automated Surface Observation System) 주요 60개 지점에서 관측된 기상자료를 이용하여 다양한 시간 척도에서의 표준강수지수(Standardized Precipitation Index, SPI)와 증발 수요 가뭄지수(Evaporative Demand Drought Index, EDDI)가 계산된다. 그리고 MODIS (Moderate-resoluation Imaging Spectro-radiometer)에서 제공하는 NDVI와 지표면기온(Land Surface Temperature, LST)으로부터 식생건강성지수(Vegetation Health Index, VHI)를 추정한다. 그런 다음 코퓰러(copula) 결합 이론을 기반으로 VHI와 가뭄지수 사이의 결합 확률분포 모델링이 수행된다. 이러한 결합 확률분포를 통해 식생 관련 가뭄의 가능성과 다양한 기상학적 가뭄 시나리오에 대한 민감도를 정량화할 수 있게 된다. 분석은 우리나라 전역의 산림지역을 중심으로 수행되었다.
2. 자료 및 연구방법
2.1 자료
한국 기상청에서 운영 중인 ASOS 60개 관측지점의 일 강수량, 일 최고기온, 일 최저기온, 일 상대습도, 일 평균풍속이 이용되었다(http://data.kma.go.kr). 자료 기간은 2000년 1월부터 2019년 12월이다. Fig. 1은 60개 관측지점의 위치를 보여준다.
MODIS에서는 위성으로부터 수집된 위성영상 자료의 DB를 구축하고 대기보정 및 Geolocation 등 Level 처리를 걸쳐 제작한 Landcover, LST, NDVI 등의 다양한 product를 제공하고 있다(Park and Kim, 2009). 본 연구에서는 MODIS에서 제공되는 MOD13A3 product의 NDVI 자료를 이용되었다. 적용된 자료의 시간 해상도는 월-단위이고 공간 해상도는 1-km이다(https://lpdaac.usgs.gov/products/mod13a3v006/). 자료 기간은 2001년 1월부터 2019년 12월이다. 본 연구에서는 기상청 60개 지점의 위치를 중심으로 반경 20-km인 원 내부에 있으면서 대분류 토지피복도에서 산림지역에 해당하는 픽셀의 NDVI 공간 평균값을 해당 관측지점에서의 NDVI로 간주하였다. 이때 반경 20-km는 Mittelbach et al. (2001)에 의해 지리적 범위와 생태학적 연관성을 기반으로 정의된 공간적 규모 중 지역적 규모(0-20 km)를 적용한 것이다.
LST는 MODIS의 MOD11B3 product가 이용되었다. 자료의 공간 해상도는 6-km이며, 시간 해상도는 월-단위이다(https://lpdaac.usgs.gov/products/mod11b3v006/). 자료 기간은 2001년 1월부터 2019년 12월이다. NDVI와 마찬가지로 각 지점에서 산림지역에 해당하는 픽셀의 공간 평균값이 추출되었다.
2.2 식생지수
각 지점의 산림지역에 해당하는 공간 평균된 NDVI는 특정 연도의 월별로 아래와 같은 식을 이용하여 식생상태지수(Vegetation Condition Index, VCI)로 환산된다(Kogan, 1997).
여기서 NDVI는 각 지점의 위치를 중심으로 반경 20-km 원 내에 있는 산림지역에서 관측된 NDVI의 공간 평균값이며, NDVImin과 NDVImax는 해당 월에 대해 2001년부터 2019년 기간에 관측된 NDVI의 최솟값과 최댓값이다.
비슷한 절차를 이용하여 온도상태지수(Temperature Condition Index, TCI)는 LST를 이용하여 아래와 같이 계산된다.
여기서 LST는 각 지점의 위치를 중심으로 반경 20-km 원 내에 있는 산림지역에서 관측된 LST의 공간 평균값이며, LSTmin과 LSTmax는 해당 월에 대해 2001년부터 2019년에 관측된 LST의 최솟값과 최댓값이다.
마지막으로, VHI는 아래와 같이 추정된다.
여기서 는 일반적으로 0.5이며, 본 연구에서도 0.5가 적용되었다(Kogan, 1997).
2.3 가뭄지수
SPI는 대기로부터의 수분공급이 부족할 때 가뭄이 발생한다는 관점에서 만든 가뭄지수이다. 즉, SPI는 강수량만을 이용하여 가뭄을 식별한다(McKee et al., 1993). 국내외에 많은 관련 연구사례가 있다(Chang et al., 2006; Kim et al., 2011). SPI는 시간 척도에 따른 이동평균 월 강수량을 이용하여 계산되며, 음의 값을 가질수록 심한 가뭄 상태임을 나타낸다.
Hobbins et al. (2016)에 의해 제안된 EDDI는 대기의 과도한 수분 수요에 의해 가뭄이 발생한다는 관점에서 만들어진 가뭄지수이다. EDDI는 참조 작물 증발산량(Reference crop evapotranspiration, Eo)을 이용하여 가뭄을 식별한다. 본 연구에서 사용된 Eo는 Penman-Monteith 방법을 이용하여 일 단위로 계산된다(Allen et al., 1998). EDDI도 SPI와 마찬가지로 다양한 시간 척도에 대한 이동평균 Eo 시계열을 이용하여 계산되나, 양의 값을 가질수록 심한 가뭄임을 나타낸다(Yao et al., 2018). SPI와의 비교의 용이성을 위하여 EDDI에 (-)부호를 붙여서 nEDDI (즉, negative EDDI)가 실제 분석에는 이용된다. EDDI에 관한 국내 적용사례는 Won et al. (2018)과 Won and Kim (2020)에서 찾아볼 수 있다.
2.4 SPI와 nEDDI를 VHI와 코퓰러 결합한 생태학적 가뭄모형
다변량 분포의 의존 구조는 다변량 정규 분포와 같은 고전적 분포를 사용하여 구성할 수 있다(Laux et al., 2011). 그러나 식생과 기후변수 사이의 의존성은 일반적으로 매우 복잡하며 시간과 공간 모두에서 다양하다. 따라서 고전적인 방법은 자료의 종속 구조를 설명하는 데 적합하지 않을 수 있다(Bárdossy and Pegram, 2009; Kim et al., 2012). 코퓰러는 식생과 기후변수 사이의 결합 의존 구조를 모형화하는 수단을 제공한다. 또한 다양한 가뭄지수들 사이의 결합 의존 구조를 모형화하기 위해 적용되기도 한다(Won et al., 2020a). 즉, 코퓰러는 한계(marginal) 분포에 대한 제한이 없이 다변량 자료들 사이에 존재하는 종속성을 모형화할 수 있다(Ryu et al., 2012). 따라서 본 연구에서는 코퓰러 이론을 도입하여 VHI와 각 가뭄지수(즉, SPI 또는 nEDDI)의 결합 확률분포를 모형화하였다. Sklar의 정리에 따르면(Sklar, 1959) VHI (X1으로 표시)와 SPI (또는 nEDDI) (X2로 표시)의 결합 누가확률분포 F(x1, x2)는 아래와 같이 표현할 수 있다.
여기서 과 는 VHI와 SPI (또는 nEDDI)의 한계 누가확률분포(Cumulative probability distribution function, CDF)로서 u1과 u2을 의미하며, C는 코퓰러 함수이다.
결합 확률분포를 모형화하기 전에 각 변수, 즉 VHI 및 SPI (또는 nEDDI)에 대해 적절한 한계 확률분포를 결정해야 한다. 전 기간별 또는 계절별 VHI의 최적 확률분포는 Normal 분포, Log-Normal 분포, Gamma 분포, Weibull 분포, Log-Logistic 분포, GEV 분포를 포함하여 일반적으로 사용되는 6개의 이론적 확률분포를 비교했다. 각 분포의 매개변수는 최대 우도 방법으로 추정되었다. Chi-square 적합도 검정을 기반으로 최적 분포를 선택했다. SPI와 nEDDI는 유도 과정의 특성상 표준정규분포를 따를 수밖에 없으므로 표준정규분포가 최적 분포로 선택되었다. 최적 한계 확률분포가 결정되면 결합 확률분포를 모형화하기 위해 적절한 코퓰러 함수가 필요하다. 본 연구에서는 수문기상학 응용 분야에서 널리 사용되는 몇 가지 코퓰러 함수, 즉 Gumbel, Frank, Clayton, Gaussian, Student-t 코퓰러를 이용했다(Salvadori and De Michele, 2004). 코퓰러 함수의 매개변수는 최대 우도 방법을 이용하여 추정되었다. 이때 우도를 구성하기 위한 이변량 경험적 누가확률분포를 구하기 위하여 Zhang and Singh (2006)이 제안한 이변량 도시위치공식이 적용되었다. VHI와 SPI (또는 nEDDI) 사이의 종속 구조를 가장 잘 포착하는 코퓰러는 Akaike information criterion (AIC)를 이용하여 결정되었다(Sadegh et al., 2017). 전 기간 분석에서는 19*12개(즉, 19년*12개월)의 VHI-SPI (또는 nEDDI) 쌍을 이용하여 최적 코퓰러 함수가 결정되었으며, 계절별(봄: 3 ~ 5월, 여름:6 ~ 8월, 가을: 9 ~ 11월, 겨울: 12 ~ 2월) 분석에서는 19*3개(즉, 19년*3개월)의 VHI-SPI (또는 nEDDI) 쌍이 최적 코퓰러 함수의 결정에 이용되었다.
VHII와 SPI (또는 nEDDI)의 결합 확률분포, 즉 Eq. (4)가 주어지면 설정된 SPI 또는 nEDDI 시나리오에서 VHI의 조건부 확률분포를 도출할 수 있다. 실제로 X2 ≦ x2가 주어지면 X1 ≦ x1의 특정 조건부 확률에 관심이 있을 수 있으며 다음과 같이 표현할 수 있다(Zhang and Singh, 2007).
Eq. (5)는 다양한 SPI (또는 nEDDI) 조건에서 VHI의 조건부 확률분포를 계산하기 위해 적용된다. 사실 u1 사상은 u1이 특정 임곗값을 초과하지 않는 경우 “위험”으로 정의될 수 있다(Salvadori and De Michele, 2004). VHI는 40 이하일 때 가뭄을 나타내며, 0에 가까울수록 가뭄의 심화를 의미한다(Ghaleb et al., 2015; Orimoloye et al., 2019). 이 때 VHI가 40 이하인 값에 대응하는 누가확률값은 약 0.3으로 산정되어, 본 연구에서는 uVHI ≦ 0.3인 경우 식생이 생태학적인 가뭄 상태(즉, 위험 상태)에 있는 것으로 간주하였다. 물론, 다른 VHI 임곗값(예: uVHI ≦ 0.1)을 사용하여 생태학적인 가뭄의 민감도를 조사하는 것도 가능할 것이다. 본 연구에서는 대기로부터의 수분공급과 대기의 수분 수요 두 가지 시나리오에 초점을 맞추었다. 첫 번째는 대기로부터의 수분공급이 부족한 시나리오, 즉 SPI가 -1 이하인 시나리오이다. 이는 표준정규분포를 따르는 SPI에 의해 SPI가 -1 이하일 확률인 uSPI ≦ 0.1587가 조건부로 주어지게 된다. 두 번째는 대기의 수분 수요가 과도한 시나리오, 즉 nEDDI가 -1 이하인 시나리오이다. 이 또한 표준정규분포를 따르는 nEDDI에 의해 nEDDI가 -1 이하일 확률인 un EDDI ≦ 0.1587가 조건부로 주어지게 된다. VHI와 SPI (또는 nEDDI)의 설정된 결합 확률분포를 기반으로, 다양한 VHI 임곗값 및 SPI/nEDDI 시나리오가 Eq. (5)에 의해 비슷한 방법으로 결정될 수 있다.
3. 결 과
3.1 가뭄지수의 시간 척도 결정
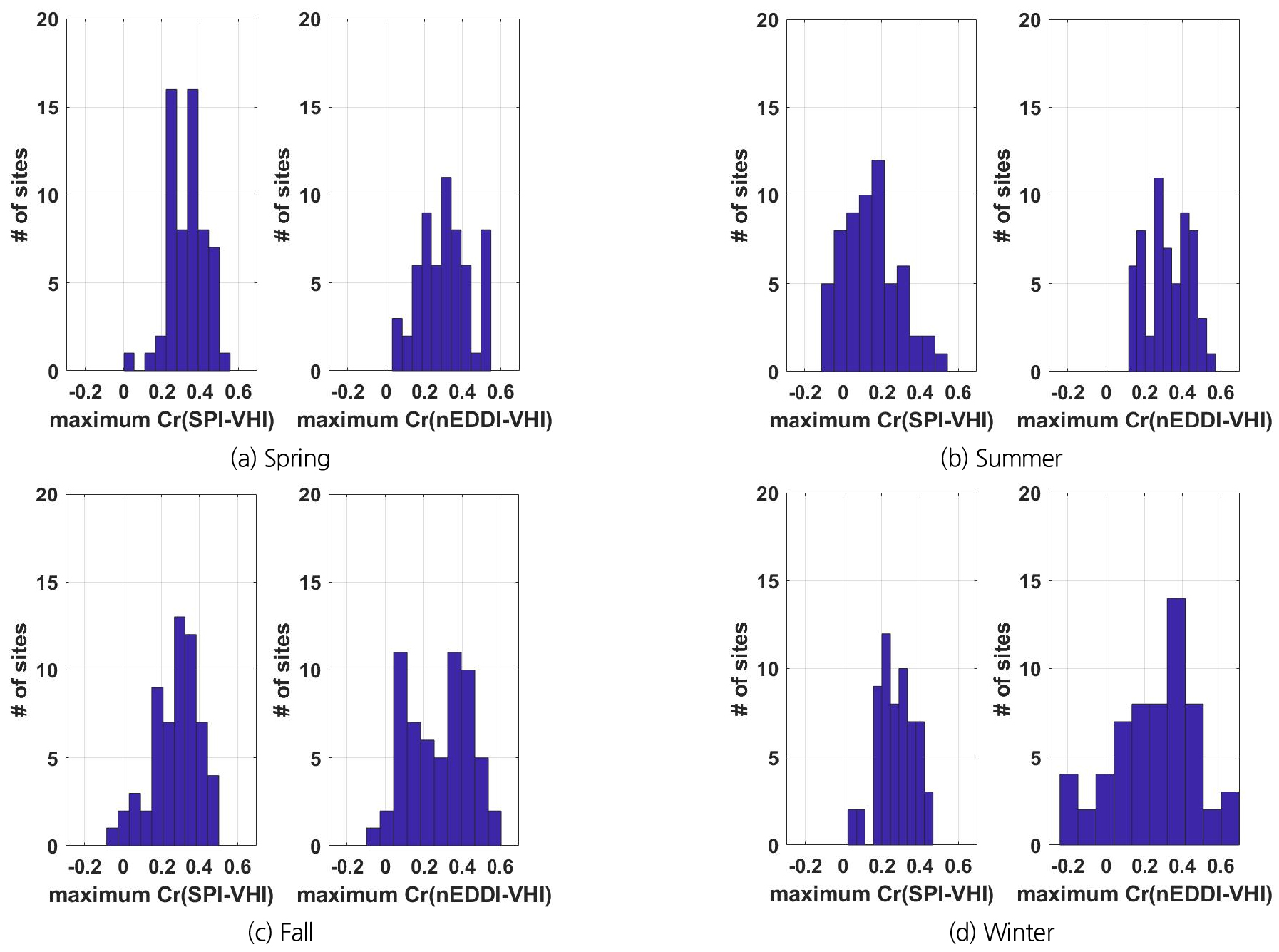
SPI와 EDDI와 같은 가뭄지수들은 원하는 시간척도(수 일, 수 주, 수개월)에 따라 계산될 수 있다. 본 연구에서 SPI와 nEDDI는 2001년부터 2019년에 대해 시간 척도 1- ,2-, …, 12-개월에 대해 산정되었다. 1-,2-,…,12-개월의 다양한 시간 척도별 SPI (또는 nEDDI)와 VHI의 상관관계를 분석하였다. 지점별로 계절별로 시간 척도별로 SPI (또는 nEDDI)와 VHI의 교차상관계수는 매우 큰 차이를 보였다. 이는 가뭄지수와 VHI와의 상관관계가 지역별로 계절별로 매우 상이하다는 것을 의미한다. 또한 같은 가뭄지수라 할지라도 어떤 시간 척도의 가뭄지수인지에 따라(즉, 예를 들어 시간 척도 6-개월의 SPI인지, 시간 척도 12-개월의 SPI인지에 따라) VHI와의 상관계수가 매우 다양하게 분포되어 있음을 알 수 있었다. 지점별로, 계절별로 VHI와의 교차상관계수가 가장 높은 가뭄지수(SPI 또는 nEDDI)의 시간 척도를 결정하였으며, 그에 대응하는 교차상관계수의 히스토그램을 Fig. 2에 계절별로 나타내었다. Fig. 2의 횡축은 교차상관계수의 구간을 나타내며, 종축은 각 교차상관계수 구간에 속하는 지점의 개수를 의미한다. 즉, 막대의 총합은 총 지점 수인 60개이다. 봄, 가을, 겨울에는 SPI와 nEDDI의 VHI와의 상관관계가 서로 비슷하였으나, 여름에는 nEDDI와 VHI의 상관관계가 더 높았다. SPI는 봄에 VHI와의 상관관계가 가장 높았으며, 여름에 VHI와의 상관관계가 가장 낮았다. nEDDI는 여름과 봄에 VHI와의 상관관계가 가을과 겨울에 비해 상대적으로 더 높았으나, 연 중 비교적 일정한 상관관계를 보여주고 있었다.
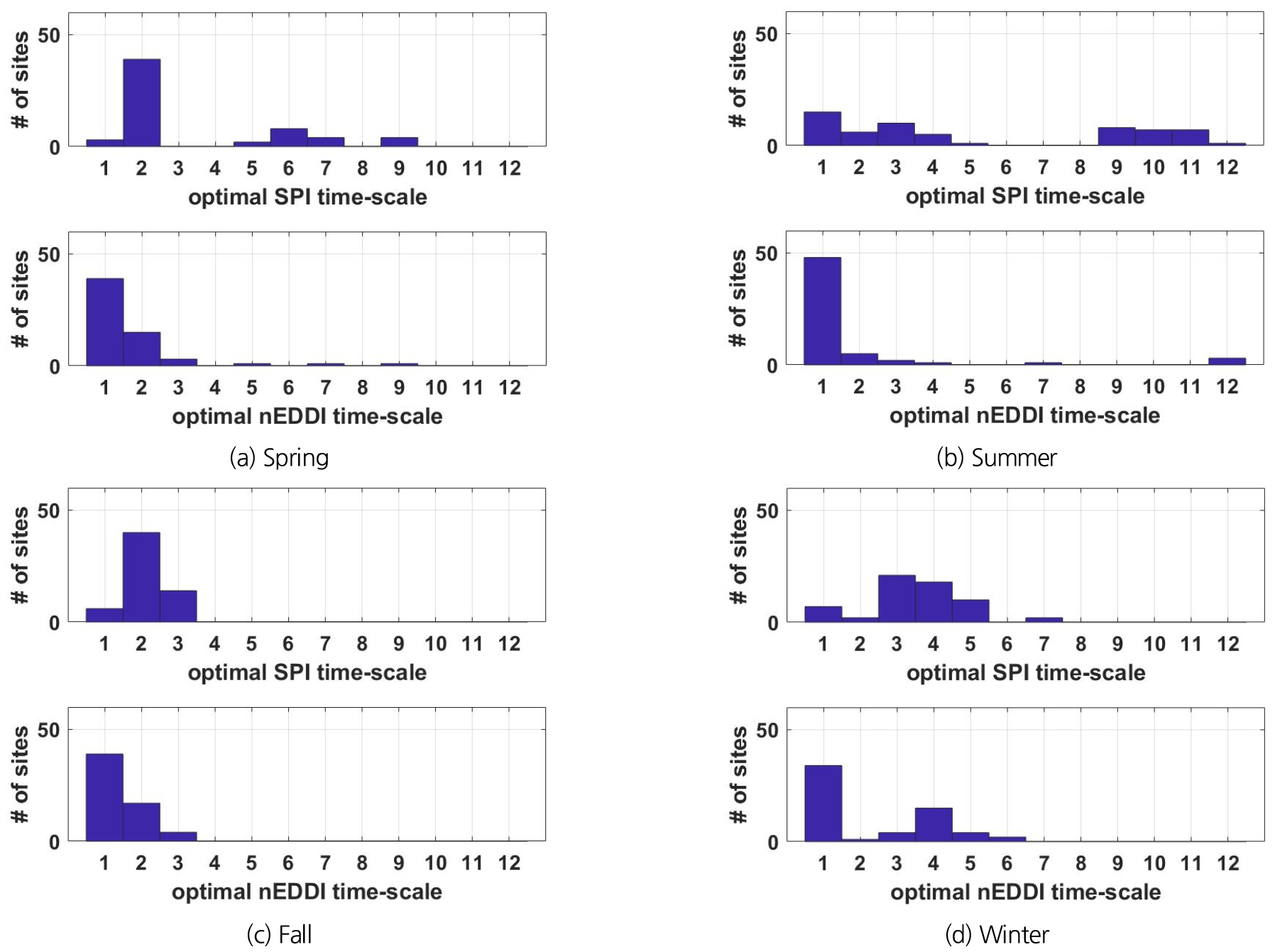
Fig. 3은 VHI와의 상관관계가 가장 높은 가뭄지수별 시간 척도를 보여준다. 본 연구에서는 VHI와의 상관성이 가장 좋다는 의미에서 이러한 시간 척도를 최적 시간 척도라고 명하였다. 계절에 상관없이 SPI의 최적 시간 척도가 nEDDI 보다 더 길었다. Fig. 3의 SPI에 대한 최적 시간 척도의 결과로부터 우리나라 산림 식생은 1 ~ 2개월의 상대적으로 짧은 기간에 대기로부터의 수분공급 부족보다는 3 ~ 4개월 또는 5 ~ 6개월 기간에 걸쳐 누적된 수분공급 부족에 의해 더 영향을 받고 있음을 발견할 수 있었다. 추후 산림이 아닌 초지에 대한 같은 분석 시에는 어떤 결과가 얻어질지 살펴볼 필요가 있을 것이다. 가뭄지수에 상관없이 최적 시간 척도가 긴(9 ~ 12개월) 지점들이 여름에 가장 많이 나타났으며, 봄과 가을에는 대부분의 지점들이 짧은 시간척도(1 ~ 3개월)를 보였다. VHI에 대한 nEDDI의 최적 시간 척도는 1 ~ 2개월 정도였다. 대기의 과도한 수분 요구량에 의한 생태학적인 가뭄의 측면에서 볼 때, 우리나라 산림 식생은 장기간의 점진적인 대기의 과도한 수분 요구 환경보다는 갑작스러운 대기의 수분 수요가 발생할 때 식생이 더 민감하게 반응한다는 것을 의미한다.
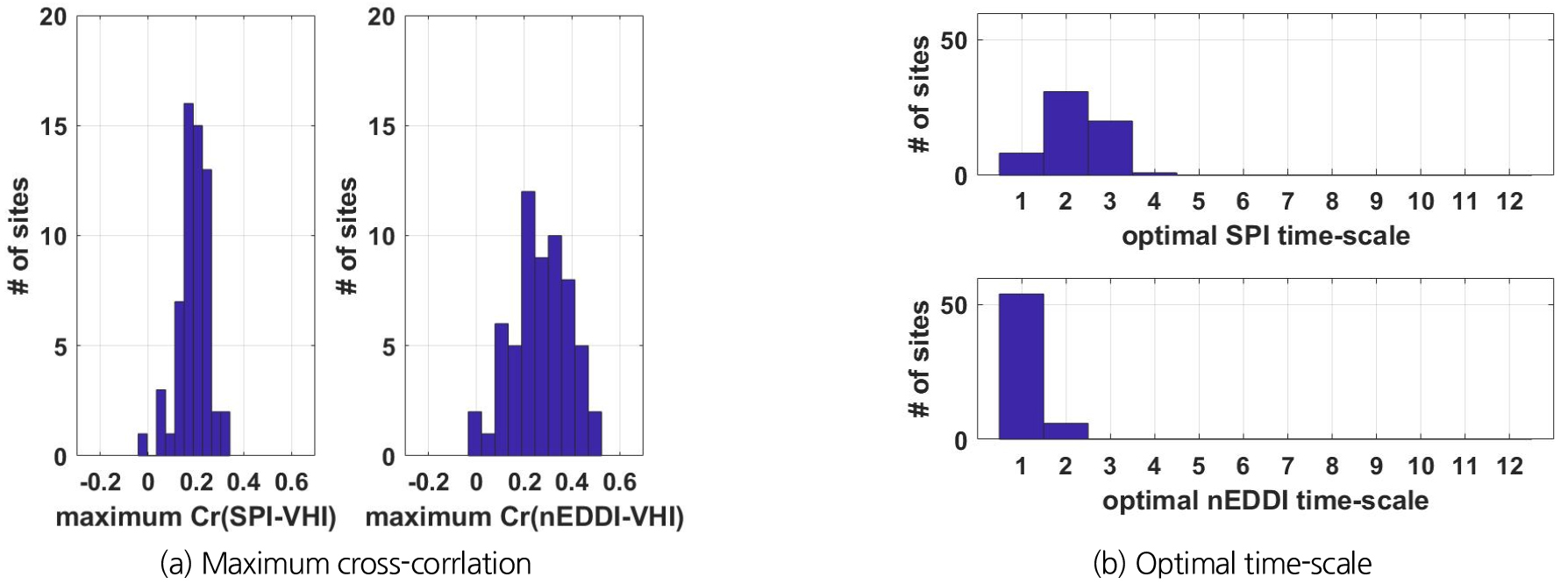
전체 자료를 모두 사용하여 가뭄지수의 최적 시간 척도와 그에 대응하는 VHI와의 교차상관계수의 분포를 Fig. 4에 나타내었다. 계절별 분석과 비슷하게, SPI 보다는 nEDDI의 교차상관계수가 더 높았으며, nEDDI의 최적 시간 척도가 SPI 보다 더 짧음을 발견할 수 있다.
3.2 코퓰러 기반 접근방법의 예시 결과
이번 절에서는 대구 지점의 자료를 이용하여 주어진 SPI (또는 nEDDI) 조건에서 산림 식생 관련 가뭄의 가능성을 정량화하기 위한 코퓰러 기반의 결합확률분포의 적용에 대한 예시가 설명된다. 본 연구에서는 자료를 봄(3 ~ 5월), 여름(6 ~ 8월), 가을(9 ~ 11월), 겨울(12월 ~ 2월)로 각각 구분하여 계절별로 분석을 수행하였으며, 모든 자료를 이용한 전체 기간에 대한 분석도 함께 수행하였다. 즉, 5개의 시기(봄, 여름, 가을, 겨울, 전체)에 대한 분석이 수행된 셈이다. 시기별 VHI에 대한 적절한 한계 분포가 먼저 결정되었다. SPI와 nEDDI의 경우에는 표준정규분포가 한계 분포로 선택되었다. 그런 다음, 한계 분포에 결합하여 제안된 코퓰러 기반 방법을 사용하여 결합 확률분포를 구성했다. 결합 확률분포가 결정되면 주어진 SPI 또는 nEDDI 하에서의 VHI의 조건부 분포가 획득될 수 있다. 이때, 시기별 가뭄지수별 가뭄지수의 시간 척도는 앞서 선정된 최적 시간 척도가 적용되었다. 참고로 대구 지점의 경우 최적 시간 척도는 Table 1과 같다. Table 1을 통해 알 수 있는 사실은 여름철 대구지점의 산림 식생은 대기의 수분 공급과 수분 수요에 대해 매우 다르게 반응한다는 것이다. 여름철 대구지점의 식생은 대기의 수분 공급이 11개월에 걸쳐 장기적으로 부족할 때 가장 민감하게 반응하였으며, 대기의 수분 수요 측면에서는 1개월과 같이 단기간의 갑작스러운 수분 요구에 대해 가장 민감하게 반응하였다.
Table 2는 VHI를 위해 적용된 한계 분포와 시기별 chi-square 검정의 p-값 통계를 나타낸다. 최적 한계 분포의 p-값이 두꺼운 글씨체로 표기되어 있다. 가장 적합한 코퓰러는 시기별로 다르다. 이는 VHI와 SPI (또는 nEDDI)의 상호작용이 계절마다 다르기 때문이며, 따라서 후보군 중에서 최적의 코퓰러 함수를 선택하는 것이 중요하다는 것을 의미한다. Fig. 5는 계절별 서로 다른 코퓰러 함수의 AIC, 선정된 최적 코퓰러의 Q-Q plot, SPI (또는 nEDDI)에 의한 기상학적 가뭄 시나리오(SPI < ‒1 또는 nEDDI < ‒1)에서의 VHI의 조건부 분포를 보여준다. 두 개의 기상학적 가뭄 시나리오에 대한 VHI의 조건부 분포를 살펴보면, 봄과 가을에는 대기로부터의 수분공급 부족이 대기의 과도한 수분 요구보다 생태학적 가뭄에 더 중요한 역할을 하고 있음을 시사한다. 반대로, 여름과 겨울에는 증발산에 의한 가뭄이 강수량에 의한 가뭄보다 산림 식생에 더 많은 영향을 미치고 있음을 발견할 수 있다. 특히 식생의 성장기인 여름에 대기의 과도한 수분 요구 상황이 전개되면 대구 주변의 산림 식생은 매우 민감하게 반응하여 생태학적 가뭄(본 연구에서는 uVHI ≦ 0.3을 생태학적 가뭄으로 정의)이 발생할 가능성이 큼을 말해주고 있다.
Table 1.
Optimal time-scale for SPI and nEDDI at Daegu site
| Optimal time-scale (month) | Spring | Summer | Fall | Winter | Year |
| SPI | 2 | 11 | 2 | 4 | 3 |
| nEDDI | 2 | 1 | 1 | 4 | 1 |
Table 2.
Goodness-of-fit statistics (Chi-square p-value) of different theoretical distribution for VHI in different seasons
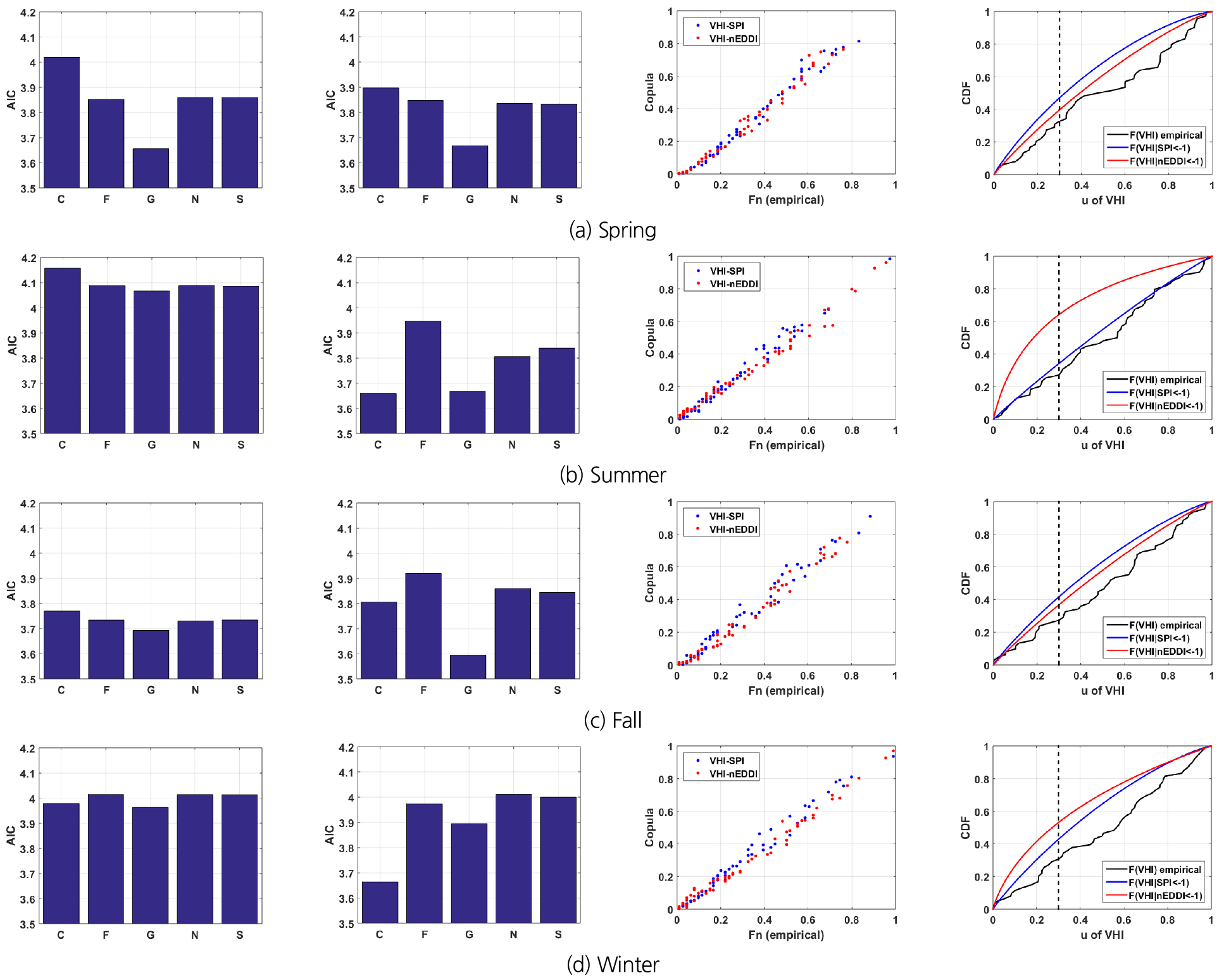
Fig. 5.
AIC values of five copulas for VHI and SPI (Far left) (C, F, G, N, and S indicates Clayton, Frank, Gumbel, Normal, and Student-t copula, respectively), AIC values of five copulas for VHI and nEDDI (Center to left), Q-Q plot using best-fitted copula (Center to right), and conditional CDF of VHI under two meteorological drought scenarios: SPI < ‒1 and nEDDI < ‒1 (Far right)
3.3 VHI와 SPI 사이의 의존성의 공간적인 패턴
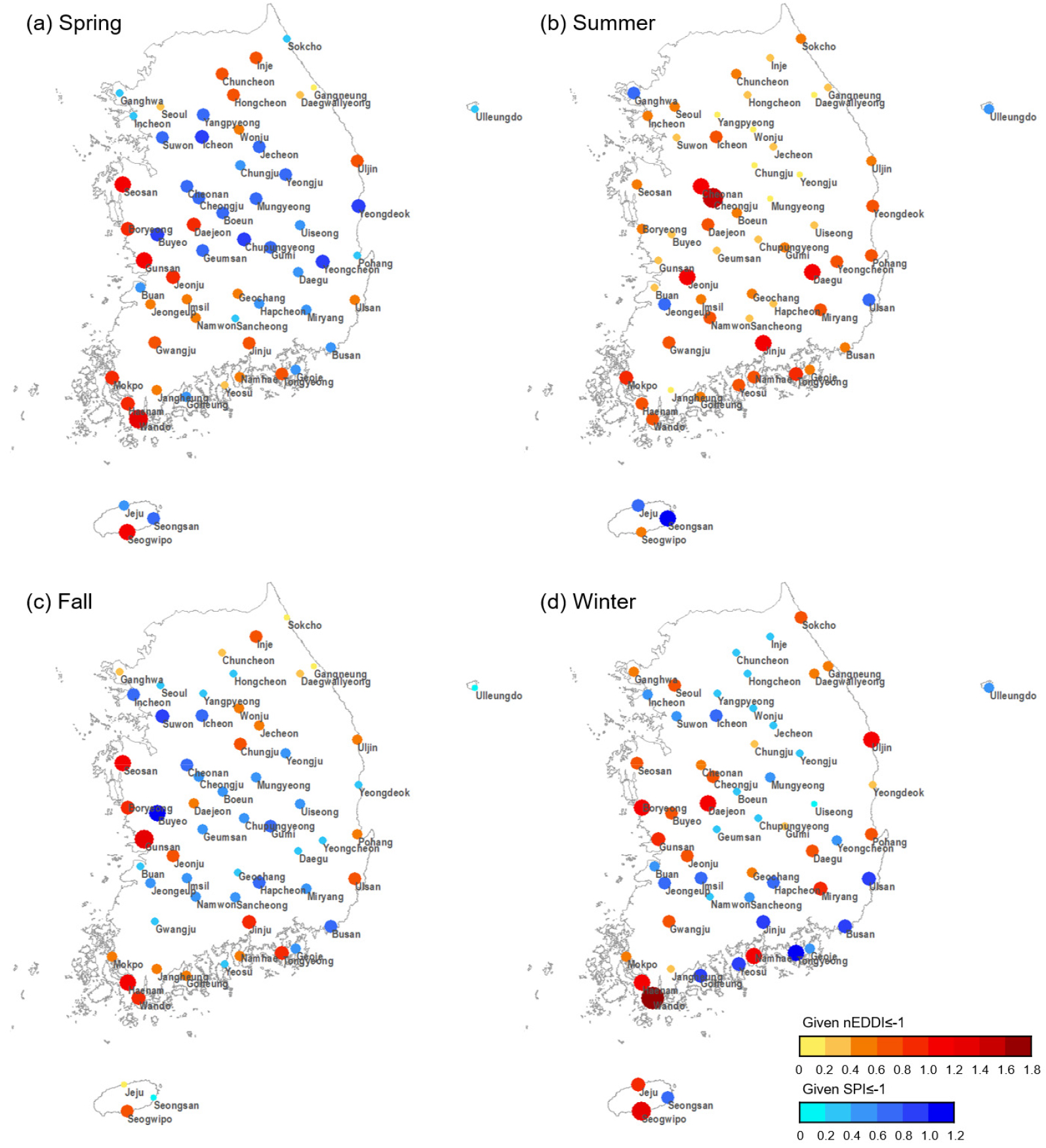
우리나라 전국 60개 지점 주변의 산림지역에 대해, 최적 시간 척도의 SPI가 -1보다 작은 강수 시나리오에서 조건화된 식생과 관련된 생태학적 가뭄(uVHI ≦ 0.3)의 공간 패턴을 조사하였다. 이를 통해 식생이 대기로부터의 수분공급에 민감한 지역을 결정할 수 있었다. 여기서 강조하여야 할 것은 일단 코퓰러 기반의 결합확률분포가 구축되면 사용자에 의해 정의된 VHI의 가뭄 임계치(본 연구의 경우에는 uVHI = 0.3)를 사용하여 사용자가 설정한 가뭄 상황에 대한 위험 지도를 작성할 수 있다는 것이다.
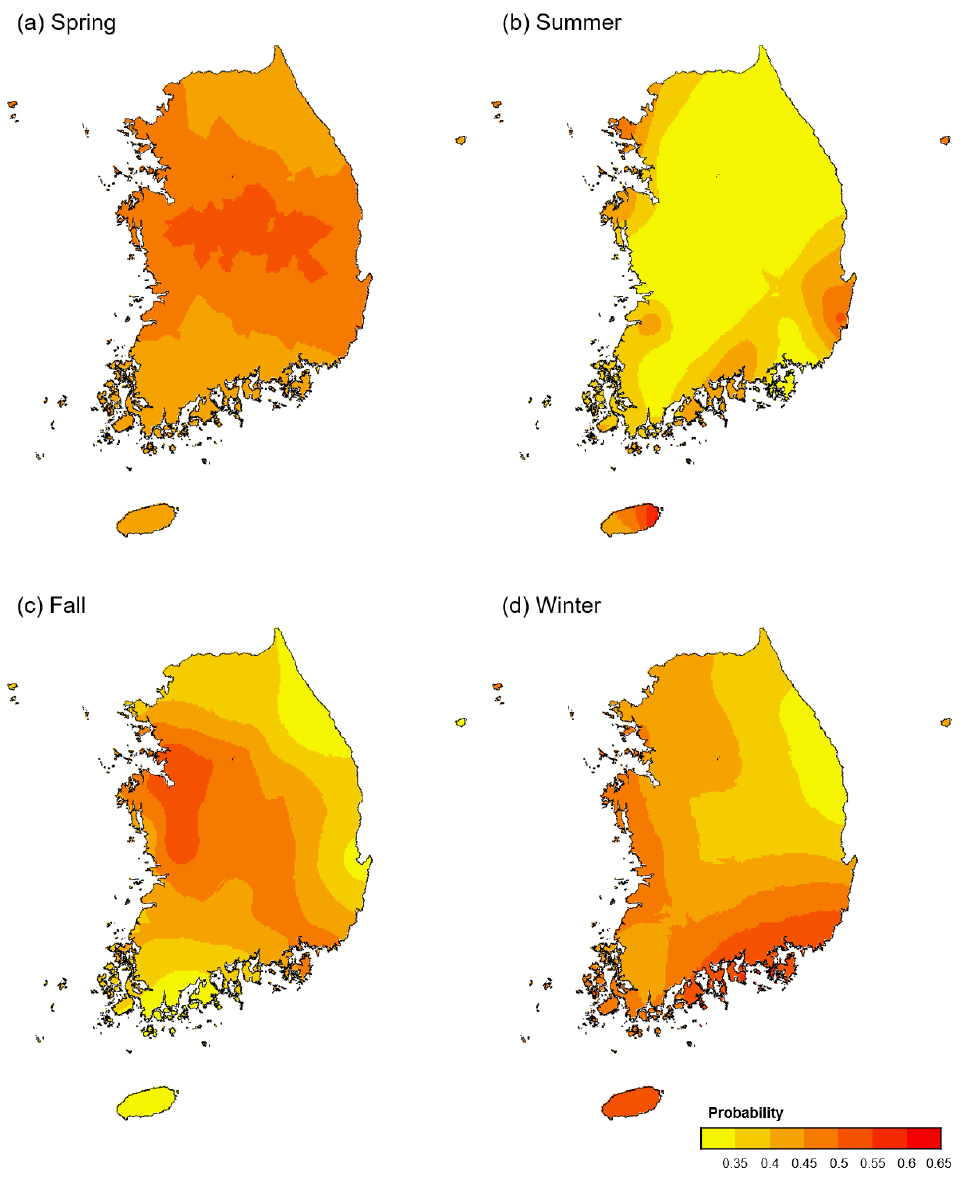
Fig. 6은 계절별 강수 시나리오에서 식생 관련 생태학적 가뭄의 확률을 나타낸다. 봄철 동안 낮은 강수량에서 가뭄의 가능성이 높은(> 50%) 지역은 충북 및 경북 산악지역에 집중되어 있다(Fig. 6(a)). 강수량의 증가는 이들 지역에서 가뭄 위험을 낮은 수준으로 줄이는 데 긍정적인 영향을 미친다. 여름철에는 낮은 강수량에서 산림 식생의 가뭄 가능성이 많이 증가한 지역이 대폭 줄어든다. 그러나 제주 동부지역과 울산 부근에서 생태학적 가뭄 가능성의 큰 증가를 살펴볼 수 있다(Fig. 6(b)). 가을철 동안 낮은 강수량에서 가뭄의 가능성이 큰 지역은 경기 남서부와 충남 내륙지역에 분포되어 있으며(Fig. 6(c)), 겨울철에는 남해안 지역의 산림이 강수량에 민감하게 반응하여 생태학적 가뭄 가능성을 증가시키고 있음을 발견할 수 있다(Fig. 6(d)). 이러한 사실은 우리나라 산림 식생은 계절에 따라 강수량에 대한 지역적 반응이 달라서 대기의 수분공급이 같은 수준이더라도 식생과 관련된 생태학적 가뭄의 공간적인 패턴은 다르게 나타날 수 있음을 의미한다.
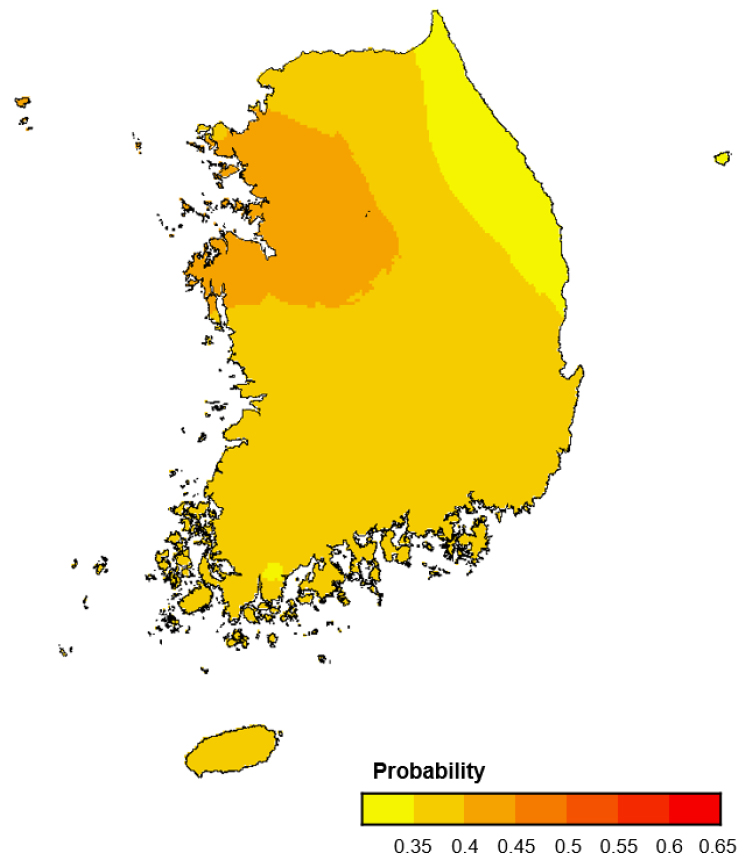
Fig. 7은 계절로 나누지 않고 전체 시계열 자료를 한 번에 분석한 결과를 보여준다. 계절 특성이 뭉개지면서 낮은 강수량에서 식생과 관련된 생태학적 가뭄의 가능성이 큰 지역이 제대로 식별되지 못함을 보여주고 있다. 연 평균적으로는 상대적으로 경기지역과 충남 북부지역의 산림 식생이 대기의 수분공급에 민감하게 반응하는 것으로 나타났으나, 민감한 정도는 계절별 분석과 비교하여 크지 않다.
3.4 VHI와 nEDDI 사이의 의존성의 공간적인 패턴
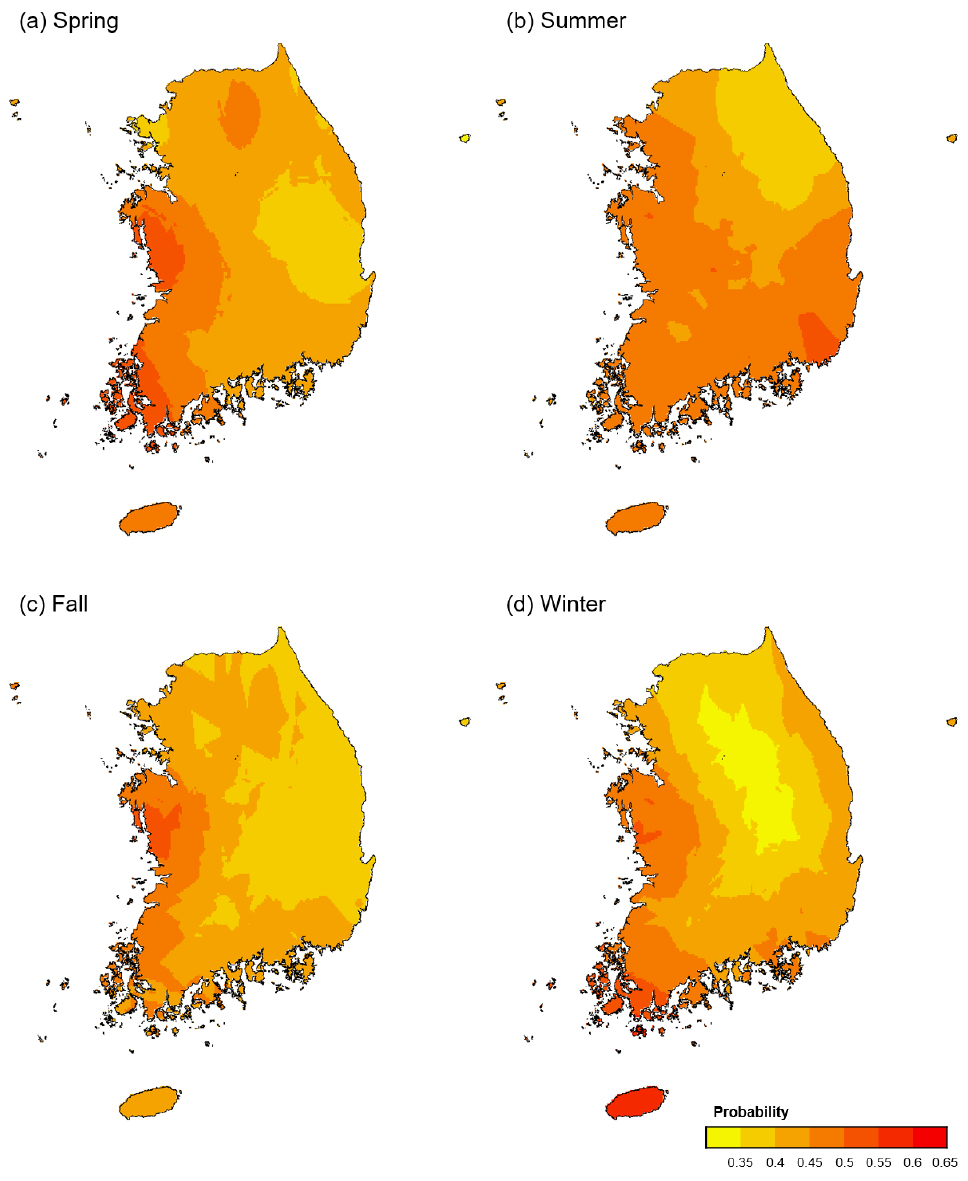
Fig. 8은 계절별 매월 잠재증발산량 시나리오에 따라 주어진 식생 가뭄(즉, uVHI ≦ 0.3의 확률) 가능성의 공간 패턴을 보여준다. 봄철 동안의 높은 잠재증발산 상태는 서해안 지역에서 식생 가뭄의 가능성을 증가시킨다(Fig. 8(a)). 충남 서해안과 전남 서해안의 산림 식생이 대기의 높은 수분 수요에 특히 더 민감한 것으로 나타났다. 여름철의 높은 잠재증발산은 부산지역의 산림 식생을 가뭄 상태로 만들 가능성이 크며(Fig. 8(b)), 가을철에는 잠재증발산에 민감하게 반응하는 산림 식생을 보이는 지역이 다른 계절보다는 많지 않다(Fig. 8(c)). 겨울철은 제주 지역의 산림 식생이 대기의 수분 수요에 민감하게 반응하여 가뭄의 가능성이 증가하고 있다(Fig. 8(d)). 계절별 차이가 상대적으로 명확했던 강수량 시나리오와는 달리, 잠재증발산량 시나리오에서는 계절과 무관하게 대체로 서해안 지역의 산림 식생의 생태학적 가뭄 가능성이 크게 나타나고 있다. 또한 강수량 시나리오의 결과(Fig. 6)와 비교할 때, 일반적으로 높은 잠재증발산 시나리오가 구현되면 산림 식생의 가뭄 가능성이 상대적으로 더 많이 증가한다.
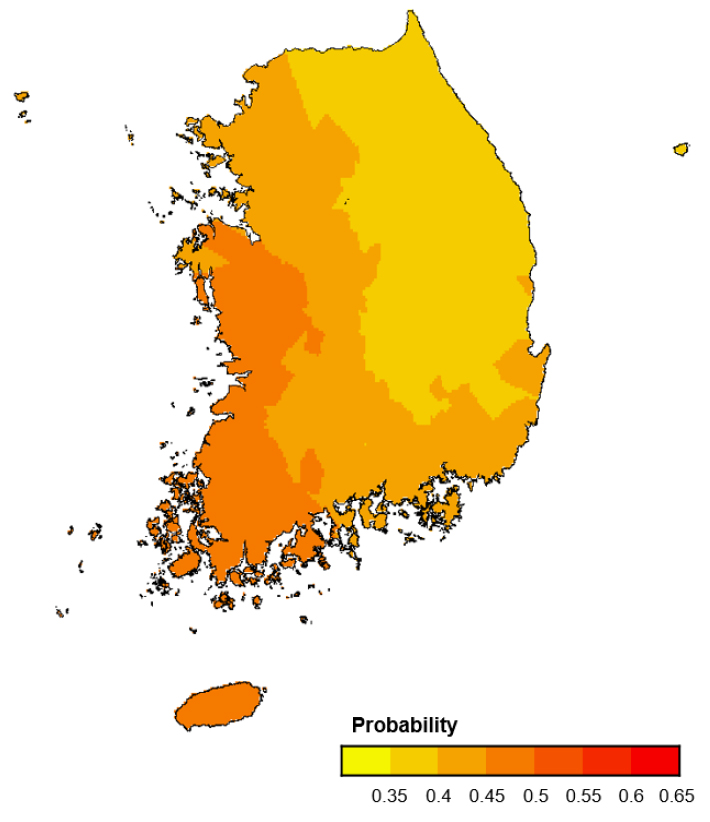
Fig. 9는 계절로 나누지 않고 전체 시계열 자료를 한 번에 분석한 결과를 보여준다. 상대적으로 서해안 지역의 산림 식생이 대기의 수분공급에 민감하게 반응하고 있으며, 강수 시나리오와 비교해 볼 때(Fig. 7), 우리나라 산림 식생은 대기의 수분공급 조건보다는 대기의 수분 수요 조건에 더 민감하게 반응하여 가뭄 상태에 처할 가능성이 증가하고 있음을 발견할 수 있다.
4. 산림 식생의 생태학적 가뭄에 미치는 강수와 잠재증발산의 상대적인 중요도
위 분석에서는 VHI의 특정 가뭄 임계치(본 연구의 경우에는 uVHI = 0.3)를 사용하여 대기로부터의 수분공급 부족에 의한 기상학적인 가뭄 시나리오 또는 대기의 과도한 수분 수요에 의한 기상학적인 가뭄 시나리오에 따른 산림 식생의 생태학적 가뭄 상황에 대한 위험 지도를 작성할 수 있었다. 이때, 가뭄 임계치로 uVHI = 0.3을 적용하였으므로, 강수 또는 잠재증발산으로부터 기인하는 기상학적 가뭄이 발생할 때 식생 가뭄의 확률이 0.3보다 크게 되면 식생은 기상학적 가뭄에 반응하고 있다는 것을 의미한다. 즉, 대기로부터의 수분공급 부족에 의한 기상학적 가뭄에 대한 식생 가뭄의 민감도 S(VHI|SPI)는 아래와 같이 표현될 수 있다.
여기서 우변의 분자의 첫 번째 항은 Eq. (5)로부터 SPI가 -1보다 작은 조건을 줬을 때 식생이 가뭄 상황(uVHI ≦ 0.3)에 들어갈 확률이다. P[SPI ≦ ‒1]은 SPI가 -1보다 작을 확률을 의미한다. 이와 비슷하게, 대기의 과도한 수분 수요에 의한 기상학적 가뭄에 대한 식생 가뭄의 민감도 S(VHI|nEDDI)는 아래와 같이 표현될 수 있다.
여기서 우변의 분자의 첫 번째 항은 Eq. (5)로부터 nEDDI가 -1보다 작은 조건을 줬을 때 식생이 가뭄 상황(uVHI ≦ 0.3)에 들어갈 확률이다. P[nEDDI ≦ ‒1]은 nEDDI가 -1보다 작을 확률을 의미한다.
민감도 S(VHI|SPI) 또는 S(VHI|nEDDI)가 큰 값을 가질수록 강수 또는 잠재증발산에 의한 기상학적 가뭄이 발생할 때 식생이 생태학적 가뭄 상황에 들어갈 확률이 더 높아지므로, Eqs. (6) and (7)을 이용하여 특정 지점 주변의 산림 식생이 계절별로 강수 또는 증발산에 의한 기상학적 가뭄에 얼마나 민감한지를 비교할 수 있다. Fig. 10은 지점별로 S(VHI|SPI)와 S(VHI|nEDDI)을 비교한 후, S(VHI|SPI)가 더 큰 지점은 푸른색 계열로, S(VHI|nEDDI)가 더 큰 지점은 붉은색 계열로 도시한 결과를 보여준다. 원의 크기는 민감도 S의 값에 비례한다.
봄철과 가을철은 유사한 패턴을 보이고 있으며, 이들의 패턴과 여름철, 그리고 겨울철의 공간적 패턴은 다르게 나타나고 있다. 봄철과 가을철 동안 충남 서부지역과 전남 서부지역의 산림 식생은 잠재증발산에 의한 기상학적 가뭄에 더 민감했지만, 수도권-충북-경북-부산으로 이어지는 축에 있는 산림 식생은 강수에 의한 기상학적 가뭄에 더 민감하였다. 제주도는 서귀포 지역의 산림 식생이 잠재증발산에 의한 기상학적 가뭄에 더 민감하게 반응하였다. 여름철 동안에는 일부 지점을 제외한 대부분의 지점 주변의 산림 식생이 잠재증발산에 의한 기상학적 가뭄에 더 민감하였다. 겨울철에는 충남 서부지역, 전남 서부지역, 동해안 지역의 산림 식생이 잠재증발산에 의한 기상학적 가뭄에 더 민감하였으며, 동남부 해안 지역의 산림 식생은 강수에 의한 기상학적 가뭄에 더 민감하다는 사실을 발견할 수 있었다.
5. 결 론
기후변화에 대한 식생의 반응에 대한 우려가 증가하지만, 다양한 기후 조건에서 식생의 생태학적 가뭄의 가능성에 대한 조사는 우리나라 전체 규모에서 현저하게 부족하다. 본 연구에서는 반사 기반의 식생 위성 정보인 NDVI와 열 기반의 식생 위성 정보인 LST를 결합하여 통합된 식생 건강성 정보를 제공하는 VHI를 이용하여, VHI와 SPI 및 VHI와 EDDI 사이의 결합 의존성을 식별하기 위한 코퓰러 기반 이변량 확률모델을 제시했다. 이를 통해 2000 ~ 2019년 기간 동안 우리나라 전역의 계절별 기상학적 가뭄 수준에 따라 식생 관련 생태학적 가뭄 가능성을 평가할 수 있었다. 저자들이 파악한 바에 따르면, 본 연구는 확률적 관점에서 대기로부터의 수분공급 또는 대기의 수분 수요에 우리나라 식생 관련 가뭄에 미치는 영향을 평가한 최초의 연구이다. 제안된 접근법을 이용하여 우리나라 전역의 식생과 관련된 조건부 가뭄 확률의 공간 패턴을 분석하였으며, 기상학적 가뭄 발생 시에 특히 더 민감한 지역에 대한 위험 지도를 생산할 수 있었다.
본 연구의 결과는 강수량 또는 잠재증발산에 의한 기상학적 가뭄 조건에서 식생 관련 가뭄 위험의 공간 패턴이 계절에 따라 현저하게 다를 수 있다는 사실을 말해준다. 봄철의 강수 부족은 충북 지역을 중심으로 식생 가뭄의 가능성을 증가시켰으며, 겨울철의 강수 부족은 남동부 해안 지역의 식생 가뭄의 가능성을 증가시켰다. 상대적으로 여름철의 강수 부족은 식생 가뭄에 큰 영향을 미치지 않는 것으로 분석되었다. 대기의 과도한 수분 수요에 의한 기상학적 가뭄은 특히 봄철과 가을철에 서해안 지역의 산림 식생에 많은 영향을 미치고 있었음을 발견할 수 있었다. 식생 가뭄에 대한 강수량 부족과 과도한 잠재증발산의 상대적인 민감도 크기는 계절에 따라 다르게 나타났으나, 대체로 서해안 지역의 산림 식생이 과도한 잠재증발산에 의한 기상학적 가뭄에 더 민감하게 반응하고 있음을 발견할 수 있었다.
본 연구는 이변량 조건부 모델을 기반으로 강수량과 잠재증발산이 식생 관련 생태학적 가뭄에 미치는 영향을 분석하는 것에 중점을 두었다. 그러나 극한 기후 현상은 동시에 발생할 수 있기 때문에 식생과 가뭄 사이의 피드백을 통합하는 데에는 이변량 결합 구조는 충분하지 않을 수 있다. 예를 들어 극심한 낮은 강수량과 고온 현상에 의한 과도한 잠재증발산이 동시에 발생하기도 하며, 실제로 가뭄은 여러 가지 기상학적 요인들에 의해 발생된다. 따라서 추후 이러한 겹쳐진 기상학적 가뭄에 대한 식생 가뭄 가능성의 분석을 위해서는 삼변량 분석이 필요할 것이다. 즉, 가뭄에 영향을 미치는 두 가지 이상의 기후변수들과 식생 사이의 복합적인 관계성을 모델링할 수 있는 다변량 분석이 요구될 것이며, 이는 추후 연구로 남겨두었다.
또한 본 연구의 주제인 식생과 기상학적 가뭄 사이의 관계와는 별개로, 식생 관련 가뭄이 인간의 교란(예: 산림 조림, 과도한 방목, 벌채, 대규모 개발사업)으로 크게 영향을 받을 수 있다는 점에 주목해야 할 것이다. 그럼에도 불구하고 제시된 기상학적 가뭄지수에 대한 식생 가뭄 가능성의 확률론적 평가는 지구 온난화 시대에 식생 반응에 대한 이해를 향상할 수 있으며 가뭄 완화 전략 개발에 유용한 정보(예: 식생 관련 가뭄에 취약하거나 기후에 민감한 지역의 식별)를 제공할 수 있을 것이다.
제한된 VHI의 기록 연수는 현재 방법론에 중대한 한계로 작용한다는 점을 지적해야 할 것이다. 장기간의 자료는 식생과 기상학적 가뭄지수의 결합 확률 분포를 더 잘 표현할 것이다. 이를 통해 식생과 기후 거동 사이의 상호작용을 더 포괄적이고 정확하게 포착할 수 있다. 또 다른 한계는 식생과 관련된 가뭄 위험을 평가하기 위한 과거 기후 관측이 정상성 기후 가정하에서 분석되었다는 것이다. 향후 연구에서는 더 다양한 수문기상학 변수(예: 토양수분)와 식생 사이의 의존성을 식별하고 식생에 대한 결합 영향을 조사하기 위해 고차원 코퓰러 모델을 사용하는 데 초점이 맞춰질 수 있을 것이며, 본 연구에서는 단순화를 위해 식생 가뭄 수준을 나타내는 특정 임곗값을 사용했으나, 더 다양한 임곗값에 관한 결과를 분석한다면 더 새로운 정보를 획득할 수 있을 것이다.