1. 서 론

안전한 먹는 물은 인간이 살아가는 데 있어 필수적인 요소이다. 상수도 관망은 정수 처리장에서 정수 처리된 물을 각 수용가에 적절한 압력 및 수질을 유지하여 공급 및 분배하는 역할을 하는 사회기반시설물이다(ME, 2010). 하지만, 최근 상수도 관망은 다양한 원인으로 인한 수질 사고(적수 사고, 수돗물 유충 사태 등)를 경험하며, 수질 문제에 대한 경각심이 높아졌다. 뿐만 아니라, 상수도 관망은 다양한 경로로 유입된 바이러스를 전파하는 사고도 발생한 사례도 보고되고 있다. 예로, 2013년 태안의 마을에서 마을 상수도를 이용하던 주민 100명 중 34명이 암으로 숨지거나 투병한 바 있다. 2022년에는 울산광역시 울주군의 마을에서 간이상수도를 이용하여 농업용수로 사용되는 지하수를 섭취한 주민들이 복통을 호소하고, 얼굴에 붉은 반점이 생기는 등의 사고가 발생한 바 있다. 이 외에도 정수장의 수돗물에서 바이러스가 검출되는 사례는 지속해서 보고되고 있어, 상수도 관망은 이러한 잠재적인 수질 사고에 노출되어 있다고 할 수 있다.

세균에 의한 수인성 질병의 대표적인 예로는 콜레라(Vibrio cholerae), 장티푸스 등이 있고, 수인성 질병을 일으키는 바이러스로는 콕사키바이러스(Coxackievirus), 아데노바이러스(Adenovirus), 노로바이러스(Norovirus), A형 간염 바이러스(Hepatitis A) 등이 있다. 이러한 바이러스들은 일반적으로 분변을 통해 환경으로 배출되어, 하수처리장을 통해 대부분의 사멸되지만 일부는 지표수와 지하수로 유입된다. 이후 수계 환경에서 존재하던 병원성 미생물들이 상수원에서 검출되거나 지하수로 존재하다 관로로 유입되어 사람에게 감염을 일으킬 수 있다. 이와 같이 상수원에는 다양한 수인성 질병을 일으키는 병원성 미생물들이 유입될 수 있고, 이는 다시 상수관을 통해 인체로 유입될 가능성이 있기에 공중보건에 대한 잠재적인 위험 요소라 할 수 있다.

일반적으로 상수도 공급 과정 중 미생물에 의한 오염을 포함하여 각종 수질 문제를 막기 위해 관망 내에 충분한 잔류염소 농도를 유지하도록 한다. Ahn et al. (2005)은 잔류염소의 적정수준 관리를 위해 관로 내 잔류염소의 분포와 시간에 따른 잔류염소 감소 모형을 제시하였다. Kim and Han (2014)의 경우 수체감소 계수와 관벽감소 계수를 추정하여 잔류염소 저감과 균등화를 위한 연구를 수행한 바 있다. Kim et al. (2017)은 잔류염소농도 최적 운영관리 모형을 개발하여 공급 과정에서 최적 잔류염소농도와 비용을 갖는 운영방안을 제시하였다. Jeong et al. (2022)에서도 유사하게 상수도 관망 내에서 격자 탐색법을 이용하여 염소 주입 및 재염소 계획 최적화 방법 그리고 공급 잔류염소농도의 균등성 평가 방법 등을 제시한 바 있다.

최근, 정수장에서 공급되는 고동도의 염소에 따른 이취미 문제와 공급과정에서 감소하는 염소농도에 따라 상수도 관망 내 적정한 잔류염소농도를 유지하기 위해 재염소(Re-chlorination) 시설을 추가하는 사례가 증가하고 있다. 재염소 시설이란 관로 내의 전략적 위치나 배수지 등에서 잔류염소 확보를 위해 추가적으로 염소를 주입하는 시설을 의미한다. 일반적으로 재염소 시설의 설치는 정수장에서 잔류염소 상한 기준(예, 1.0 mg/L)을 적용하여 수돗물 공급을 공급할 경우, 배수지 혹은 수용가에서 잔류염소 농도를 법적 잔류염소 최소 농도 (예, 0.1 mg/L) 이상으로 유지하기 어려운 경우에 설치하는 것을 권장한다 (Jeong, 2008). 재염소 시설 설치 시, 정수장의 후 염소 투입에만 의존하는 경우보다 총 염소투입량이 감소할 뿐 아니라(Yoon et al., 1998), 상수도 관망 내에 예상하지 못한 오염이 발생했을 때도 오염물의 확산을 억제할 수 있는 것으로 알려져 있다(Parks and VanBriesen, 2009).

재염소 시설 설치에 관한 연구들은 대부분 최적화 알고리즘 기반의 설계를 통해 위치와 용량을 결정한 것으로 조사되었다. Prasad et al. (2004)는 다목적 최적화 모델(Non-Sorted Genetic Algorithm, NSGA-II)을 사용하여 총 염소 투입량을 최소화하고, 최소 잔류염소 농도 이상을 만족하는 수요량을 제시하였다. Ostfeld and Salomons (2006)은 유전자 알고리즘(Genetic Algorithm, GA)을 사용하여 펌프 운영 계획과 재염소 시설의 위치 및 운영을 최적화하였다. 이와 유사하게, Lansey et al. (2007)의 연구도 수질 모델링을 통해 염소 주입량과 잔류염소 농도를 예측하고, GA를 사용하여 최적 재염소 주입 위치와 주입률을 결정한 바 있다. Moeini et al. (2023)은 EPANET-MSX (Multi Species Extension)와 Bayesian Optimization (BO)을 결합하여 상수도 관망 내 잔류염소 제약조건 등을 만족할 수 있도록 염소 주입 계획을 최적화한 바 있다.

선행연구의 대부분은 염소 주입량, 염소소독 비용, 재염소 시설 운영 비용 등이 최소가 되는 목적함수를 찾는 연구들로 요약할 수 있다. 상수도 관망의 경우 잔류염소가 다양한 외부 요인에 의해 감소할 수 있으며, 외부에서의 바이러스 유입 또한 하나의 사례라 할 수 있다. 다만, 상수도 관망 내 바이러스 유입에 따른 영향 분석을 한 사례는 Teunis et al. (2010), Lee et al. (2013), Lee et al. (2022)등의 연구만 확인되고 있다. Teunius et al. (2010)의 경우 대장균이 상수도 관망 내 유입되었을 때의 영향에 대해서 분석하였으며, Lee et al. (2013)의 경우 상수도 관망에서의 영향보다 수돗물에서의 크립토스포리디움에 대해서만 분석하였다. Lee et al. (2022)의 경우 상수도 관망 내 바이러스 유입에 따른 염소의 분포와 risk를 최소화하기 위한 재염소 시설을 검토한 바 있지만, 이 연구에서도 재염소 시설의 위치만 결정하였고 운영에 대한 부분은 고려되지 않았다.

본 연구에서는 기존 Lee et al. (2022)의 연구를 토대로 상수도 관망 내 바이러스 유입 대응을 위한 재염소 시설에서의 염소 주입 농도에 대한 분석을 추가로 수행하고자 한다. 이를 위해, 바이러스와 염소의 반응을 모의하기 위해 EPANET-MSX를 활용하였으며, 바이러스에 의함 전염 위험도 산정 방법론인 QMRA (Quantitative Microbiological Risk Assessment)를 토대로 위험도 분석을 수행하였다. 또한, 재염소 시설로 인해 추가되는 염소농도가 정상상황(바이러스 유입이 없는 경우)에서도 관망 전반에 걸쳐 목표 범위 내에서 정상적으로 운영이 되는지를 검토하기 위해 Water Quality Resilience (Resq)를 활용하였다. 최종적으로 risk와 Resq 산정 결과를 토대로 바이러스 유입 시 대비가 가능한 재염소 설계안을 제시하였다.

2. 방법론

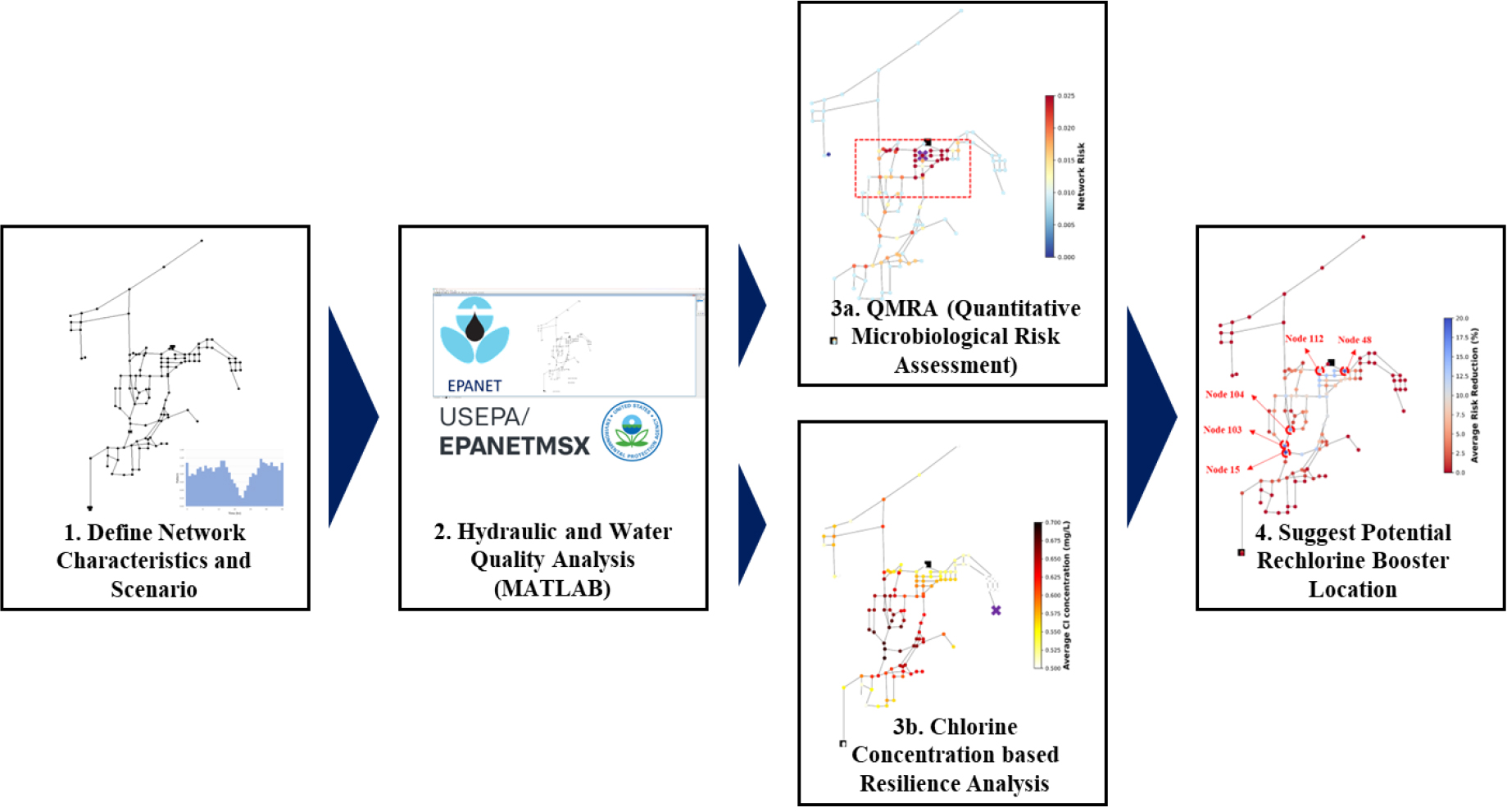
일반적으로 상수도 관망의 수질분석은 수질 계측 정보의 오류나 용수 사용량의 변동성 등으로 인한 불확실성을 내포하고 있는 것으로 알려져 있다. 특히 염소 반응계수의 경우 상수도 수원의 수질과 상수도 관망 내 운영 및 관로 재질에 따라 큰 변동성을 가지는 것으로 알려져 있다(Ahn et al., 2005; Kim et al. 2010). 이에 본 연구에서는 반응계수에 대한 분석이 수행된 관망을 선정(Fig. 1의 1번 단계)하여 분석하였으며, MATLAB을 활용한 EPANET-MSX 툴킷을 사용하여 관망 내의 염소와 바이러스의 농도 변화 및 반응을 모의(Fig. 1의 2번 단계)하였다. 모의 시 바이러스 유입 위치, 재염소 시설의 위치, 염소 주입 농도 등의 조합을 시나리오(Fig. 1의 1번 단계)로 선정하였다. Risk 결과를 토대로 관망 내 바이러스 유입 시 가장 취약한 노드를 식별하고, 바이러스가 유입됐을 경우 가장 큰 영향을 받는 노드를 식별(Fig. 1의 3a번 단계)하였다. 그리고 재염소 시설 위치에 따른 risk 감소와 염소 농도에 따른 Resq를 산정(Fig. 1의 3b번 단계)하여, 가장 효과적인 위치를 선정(Fig. 1의 4번 단계)하였다.

Fig. 1.

General overview of study

2.1 EPANET-MSX

EPANET-MSX는 EPANET의 확장된 프로그램으로 관망 내의 여러 화학종(chemical species)간 반응을 분석하는 것에 목적을 둔다. 특히 단일 화학종의 이송(Transport) 및 거동(Fate)을 파악하는 것으로 제한된 EPANET의 한계를 개선하여 여러 화학 및 생물 종(염소, 박테리아 및 기타 오염물질)간의 이송, 화학반응, 상호작용을 모의할 수 있다. 즉 EPANET은 주로 수리해석과 기본적인 단일 수질 해석에 사용할 수 있고 EPANET-MSX는 심화된 다중 수질 해석이 가능하다.

본 연구에서는 EPANET-MSX 상에서 수질 해석 시 바이러스와 염소 간의 반응을 고려하였다. 이때, 바이러스는 관망 내에서 증식되지는 않는다고 가정하였다. 시간별 염소 농도의 변화는 Eq. (1)과 같이 1차 감소(first-order decay)를 가정하여 모의할 수 있다(Boccelli et al., 2003; Thurston-Enriquez et al., 2003).

여기서, CCl,t은 t 시간에서의 염소 농도(mg/L), kA는 염소 반응 계수(1/day)이다. 관망 내 바이러스 농도 변화의 경우 Chick-Waston 식(Eqs. (2a)~(2c))으로 계산되었으며, 이때 바이러스와 반응하여 감소한 염소의 농도는 무시하였다(Poduska and Hershey, 1972).

여기서, CV,t는 시간 t에서의 바이러스 농도(genecopies/L), kB는 바이러스 반응 계수(1/day)이다.

2.2 Quantitative Microbial Risk assessment (QMRA)

본 연구에서는 바이러스 유입 시 감염위험을 추정하기 위해, QMRA를 이용하였다. QMRA는 식품, 물, 환경과 같은 다양한 환경에서 사람이 세균이나 바이러스 등의 미생물 병원체에 노출되었을 때 사람의 건강에 미치는 부정적인 영향(위험)을 양적으로 추정하는 방법이다. 이는 병원성 미생물이 가진 변이성과 불확실성을 고려하여 감염 확률을 평가하는 기술로, 미국, 네덜란드 등 각국에서 수질 관련 법규 제정이나 처리공정 평가 등에 활용하는 등 다양하게 활용되고 있다(Bahk et al., 2005).

QMRA는 총 6단계로 분석할 수 있으나, 일반적으로 위험성 확인(Hazard Identification), 노출평가(Exposure Assessment), 용량-반응 분석(Dose-Response Analysis), 위험 특성화(Risk Characterization)의 4단계로 간략화하여 수행한다(Hamouda et al., 2016). 본 연구에서도 간략화된 4단계로 QMRA를 적용하였으며, 이때 1일당 인체에 흡수될 것이라 예상되는 바이러스양(dosei)은 Eq. (3)과 같다.

여기서, Vconsumed,i는 하루 물 음용량(L), max(CV,t,i)는 시뮬레이션 기간 중 최대 Enterovirus 농도(mg/L)이다. 산정된 dose를 용량-반응 분석을 통해 실제 감염 위험으로 나타내면 아래 Eq. (4)와 같다.

여기서, k는 단일 유기체가 생존하여 감염 위치에서 감지될 확률이다(MSU, 2011). QMRA를 토대로 산정된 감염 위험도는 노드별로 산정되었기에, 바이러스 유입 혹은 재염소 위치 및 주입 농도에 따른 영향을 분석하기 위해서는 상수도 관망 전체에 대한 위험도를 정량화할 필요가 있다. 본 연구에서는 상수도 관망 전체의 감염 위험을 정량화하기 위해 노드 위험도(Node Risk), 네트워크 위험도(Network Risk), 평균 위험도(Average Risk)를 정의하였다. 각 위험도에 대해 Table 1에 정리하였다.

Node risk의 경우 특정 노드가 해당 상수도 관망에서 발생 가능한 모든 바이러스 유입 시나리오에 대한 평균적인 위험도를 의미하며, Node risk가 높은 경우 해당 노드가 일반적으로 다른 노드에 비해 임의의 바이러스 유입에 높은 위험도를 가진다고 할 수 있다. Network risk의 경우 반대로 특정 노드에 바이러스가 유입될 때 상수도 관망 전반에 미치는 위험도를 의미하며, Network risk가 높은 경우 해당 지점에 바이러스가 유입될 때 상대적으로 시스템의 피해가 큰 노드라 할 수 있다. 마지막 Average Risk의 경우 모든 바이러스 유입 시나리오에 대한 상수도 관망의 평균 Network risk로 재염소 시설 설치로 인한 영향을 비교하기 위한 지표로 사용한다.

2.3 Water Quality Resilience

앞서 상수도 관망 내 바이러스 유입에 따른 영향을 분석하기 위한 위험도 분석 방안을 소개하였다. 바이러스 유입 시 이에 대응하기 위해 일정량의 염소가 반응하게 되지만, 정상상황에서는 이러한 염소 추가 공급분이 오히려 이취미 문제를 야기할 수 있다. 이에 따라, 관망 내 각 노드에서 염소 주입 농도에 따른 Resq를 산정하였다.

Resq를 산정하기 위해서는 먼저 Water Quality Utility를 결정해야 한다. Water Quality Utility는 앞서 언급한 염소 농도의 정상범위에 대한 가중치에 해당하며, 0과 1 사이의 값을 가진다. 본 연구에서는 염소 농도가 관리자가 설정한 정상 범위 내 존재할 경우 1로, 이외의 범위에서는 선형으로 감소하고, 허용 가능한 최댓값보다 높거나 혹은 허용 가능한 최솟값보다 낮은 경우 0으로 설정하였다(Shafiqul Islam et al,. 2014). 이를 수식으로 나타내면 Eq. (5)와 같으며 이를 도식화하면 Fig. 2와 같다.

Fig. 2.

Water quality utility curve

여기서, Uj,t는 t 시간에서의 j 노드 Water Quality Utility, CCl,tj는 t 시간에서의 j 노드 염소 농도(mg/L), CCluDes는 정상범위 내 최대 염소 농도(mg/L), CCllDes는 정상범위 내 최소 염소 농도(mg/L), CClmax는 염소 농도 최대 기준치(mg/L)이다. 최종적으로 Resq의 경우 모의한 각 시간에서의 모든 절점의 Water Quality Utility의 가중 평균으로 산정할 수 있으며, 이때 수요량에 대한 가중치를 부여하여 아래 Eq. (6)과 같이 산정할 수 있다.

여기서, T는 총 모의시간(hr)이고, nnodes는 총 수요절점의 개수, 그리고 Dj는 j 노드에서의 수요량(liter per minute, lpm)이다.

3. 적 용

3.1 적용 관망

제시한 방법론은 미국 워싱턴주의 Bellingham 관망(Fig. 3)에 적용하였다. 관망 내에는 두 개의 탱크와 121개의 노드가 있으며, 급수인구는 2018년 기준으로 90,665명으로 총 11,317 lpm의 평균 수요량을 갖는다. 관망 내의 시간당 염소감소 상수 k는 0.833/day이다(Vasconcelos et al., 1997). 수질 해석을 위해 EPANET의 Extended Period Simulation을 수행하였으며, 이때 모의 시간은 탱크의 운영 주기에 따라 36시간으로 설정하였다.

Fig. 3.

Schematic of Bellingham network and demand pattern

3.2 적용 시나리오

연구 흐름은 Fig. 4와 같다. 먼저 적용 관망인 Bellingham 관망의 정보를 불러오고, 이를 토대로 기본적인 수리해석을 수행한다. 수리해석 결과는 수질 해석을 위해 “.hyd” 파일로 저장되며, EPANET-MSX는 해당 파일을 불러와 수질분석을 수행한다. 수질분석 결과 각 수요 절점(demand node; 수요량이 있는 절점)에서의 염소와 바이러스 농도가 수집되며, 이를 토대로 QMRA를 수행하여 위험도 분석을 진행한다. 해당 절차는 바이러스 유입 지점을 변경하며 반복하며, 모든 절점에서 독립적으로 수행된다.

Fig. 4.

Flowchart of study

본 연구에서는 분석을 크게 두 단계(각각 Step1과 Step2로 정의)로 구분하여 진행하였다. 먼저 Step1에서는 재염소 시설이 없는 기존 Bellingham 관망의 중앙집중식 염소 주입 조건에서의 각 절점(node)에서 바이러스 유입에 따른 위험도 분석을 수행하였다. 이는 관망의 현재 운영 상황에서 재염소 시설 신설 필요 여부를 검토하는 과정이며, 집중 관리가 필요한 지점에 대한 식별 목적 또한 있다. 이때, 바이러스는 단일 절점(node)에서만 유입되는 것으로 가정하였으며, 모든 유입 가능 지점에 대해 동일한 유입량을 주입하며 반복 수행하였다. 분석결과를 토대로, 관망 내 바이러스 유입에 대해 취약한 절점(Node risk 결과 기반)과 전체 관망에 가장 큰 피해를 주는 바이러스 유입 지점(Network risk 결과 기반)을 검토하였다. 또한, 재염소 시설 설치로 인한 효과를 비교하기 위한 기준을 수립하기 위해 Average risk를 산정하였다.

이후 Step2에서는 바이러스 유입에 대한 한계점을 개선하기 위한 추가 재염소 시설의 위치 및 염소 주입 농도를 검토하였다. 이때, 잠재적인 재염소 시설의 위치로 수원을 제외한 모든 절점(node)을 고려하였으며, 단일 재염소 시설에서 최소 0.5 mg/L에서 최대 1.0 mg/L까지 0.1 mg/L씩 간격으로 전수조사를 수행하였다. 위험도 분석 후 최소 Average risk를 확보할 수 있는 재염소 시설의 위치를 제안한다.

본 연구에서는 유입 가능 바이러스를 Enterovirus로 한정하였다. Brinkman et al. (2017)의 연구에서는 하수 표본에서 Enterovirus를 분석하였으며, 대략 7.05 × 10³ 에서 8.3 × 10⁵ genecopies/L 범위에서 검출됨을 제시한 바 있다. 본 연구에서는 해당 수치 중 가장 보수적인 수치인 8.3 × 10⁵ genecopies/ L가 지속해서 유입되는 상황으로 가정하였다. 또한, 염소와 바이러스 간 반응계수(kB)의 경우 Lee et al. (2022)에서 제시한 2.78/min을 고려하였다. 1인당 하루 음용량(Vconsumed,i)은 2 L로 가정하였으며, 감염 확률(k)의 경우 QMRA 분석에서 Enterovirus에 대해 제시한 0.00374를 적용하였다. 마지막으로, CCllDes, CCluDes, CClmax는 각각 0.1 mg/L, 1.0 mg/L, 그리고 2.0 mg/L로 설정하였다.

4. 결 과

4.1 기존 관망 위험도 분석(Step1)

Step1 분석 결과 재염소 시설이 설치되기 이전에 관망의 Average risk는 0.0154로 산정되었다. 또한, 바이러스 유입에 따른 영향을 평가하기 위해 체류시간을 분석하였으며, 최대 체류시간에 대한 정보를 Fig. 5에 표시하였다.

Fig. 5.

Maximun residence time

Fig. 5에서 확인할 수 있듯, 대부분 말단부 혹은 탱크 인근의 지역에서 높은 체류시간을 나타내는 것을 확인할 수 있다. 본 연구에서는 운영에 대한 조건은 고정하였기에, 체류시간의 경우 모든 분석에서 동일하게 나타난다.

마지막으로, Bellingham 관망의 현재 운영 상황에서의 염소 주입에 대한 Resq(=0.9998)를 분석한 결과 최소 0.1 mg/L와 1.0 mg/L를 기준으로, Node 113(Fig. 6에서 보라색 “X” 지점)에서 0.1 mg/L 이하의 염소가 주입되는 시점이 있는 것으로 나타났다. 이는, 결국 해당 절점의 경우 기존 수요량 대비 많은 양의 용수가 소비될 경우 바이러스 유입에 대한 위험도가 상대적으로 높을 가능성이 있음을 시사한다고 할 수 있다. 다만, 해당 수요절점이 전체 관망의 0.3%가량의 수요량만을 사용하고 있기에, 본 연구에서 고려한 바이러스 유입 시나리오에 대해서는 큰 영향이 발생하지 않을 것으로 추정할 수 있다.

Fig. 6.

Average Cl concentration

4.1.1 Node Risk 분석 결과

Fig. 7은 적용 관망의 Node risk의 공간적 분포를 나타낸다. Node risk (모든 바이러스 유입에 대한 해당 절점에서의 평균 위험도)는 최소 0.0083에서 0.0496으로 나타났다. 총 119개의 수요절점 중 15개 절점만 중간값인 0.0290 이상의 위험도 결과를 보여 적용 관망의 경우 해당 15개 절점에 대한 집중 관리가 필요할 것으로 판단된다.

Fig. 7.

Node risk results of step 1

해당 절점은 모두 우상단 탱크와 수원 사이(Fig. 7에서 네모 박스 지역)에 위치하고 있다. 이 지역은 탱크의 운영으로 인해 유향의 변동이 지속해서 발생하는 지역으로, 이로 인해 체류 시간이 길어짐(Fig. 5)에 따라 바이러스 유입에 따른 위험도가 커진 것으로 추정된다. 또한, 탱크가 운영되며 상대적으로 바이러스가 해당 구역에서 정체하고 있는 현상이 발생하는 영향도 있다.

이러한 이유로 인해 Bellingham 관망에서 바이러스 유입에 가장 취약한 절점은 Fig. 7에서 보라색 “X”로 표기된 39번 노드였다. 39번 노드의 Node risk는 약 0.0496으로 타 절점에 비해 긴 체류 시간을 갖기에 상대적으로 높은 위험도가 형성되었다. 다만, 수요량 자체는 그리 크지 않은 것으로 보아, 위험도의 경우 수요량보다는 주입 지점의 관망 내 위치에 영향이 더 많은 것으로 나타났다.

4.1.2 Network Risk 분석 결과

관망의 위험도에 가장 큰 영향을 주는 바이러스 유입 지점의 경우도 최소 0.0083에서 최대 0.0572의 위험도 분포를 보이고 있었으며, 이 중 중간값인 0.0328 이상의 수요절점은 11개로 바이러스 유입에 대한 지속적인 관리가 필요한 수요절점은 전체 바이러스 유입 가능 지점 대비 적은 것으로 나타났다(Fig. 8). 다만, 해당 절점에 바이러스가 유입될 경우 다른 수요절점에 비해 큰 위험도를 나타내기에 이에 대한 대비책 마련이 필요할 것으로 판단된다.

Fig. 8.

Network risk results of step 1

전반적인 추세의 경우 Node risk 분석결과와 유사하게 비교적 관망의 중심에 바이러스가 유입될 경우 위험도가 상대적으로 큰 것으로 나타났다. 이러한 경향의 주요 원인은 전반적인 체류 시간이 긴 영향도 있지만, 해당 구역이 관망의 가운데 지점에 있어 염소의 농도가 많이 저감되는 지점(Fig. 6)이기에, 바이러스 유입 시 영향이 큰 것으로 추정된다. 특히, 북쪽 탱크에서 물이 공급되는 경우, 중간 구역의 절점들은 일시적이지만, 흐름상 상류 쪽에 위치한 것과 같은 효과가 발생한다. 이에, 해당 구역에 바이러스가 유입되면, 상대적으로 타지역에 비해 바이러스가 전파될 가능성이 높다.

이에 따라 Network risk가 가장 높은 절점은 48번 노드(Fig. 8 보라색 X 지점)로, 해당 절점 또한 탱크 근방에 위치하며, 탱크의 운영 상태에 따라 많은 양의 유량이 해당 절점을 통해 흘러감을 확인하였다. 즉, Network risk의 경우 해당 절점에서의 잔존 염소가 적거나, 상대적으로 상류 쪽에 위치하여 하류에 영향을 받는 절점이 많을 경우에 높아지는 것으로 추정된다.

4.2 재염소 시설 설계(Step2)

Step1에서는 기존 관망에서 위험도 분석을 수행하였으며, 이를 토대로 0.0154의 Average risk를 나타냄을 확인하였다. Step2에서는 해당 Average risk를 저감할 수 있는 재염소 시설의 위치와 염소 주입 농도를 분석하였다. 분석 시 재염소 시설은 한 개 지점만 설치하는 것으로 가정하였고, 모든 수요절점을 잠재적인 재염소 시설 설치 지점으로 고려하였다. 또한, 염소 주입 농도는 0.5 mg/L에서 1.0 mg/L까지 0.1 mg/L 간격으로 증가시키며 분석하였다.

분석결과 15번 절점에서 1.0 mg/L를 주입할 경우 약 31.9% 정도 Average risk를 저감할 수 있는 것으로 나타났다(Table 2). 이외에도 48번, 103번, 104번, 112번 절점에서도 주입 염소 농도에 따라 적게는 15.22%에서 21.20%까지 저감이 가능한 것으로 나타났다. 바이러스가 염소와 반응하여 저감(Eq. (2))하기에 염소 농도가 많이 주입될수록 Average risk는 낮아지는 것을 확인하였다. 또한, 일반적으로 수원과 가깝거나 우상단 탱크와 가까운 곳에 재염소 시설을 설치할 때 비교적 효과가 큰 것으로 나타났다(Fig. 9).

Fig. 9.

Average risk reduction results of each rechlorine booster location with 0.5 mg/L injection

Fig. 10.

Node risk difference between without and with rechlorine booster (0.5 mg/L) at node 112

다만, Resq의 경우 다른 양상을 보였으며, 대부분 경우 추가 염소 주입으로 인해 기존 대비 낮은 Resq 값을 나타내었다. 이는 재염소 시설로 인한 염소 주입으로 염소 농도가 일시적으로 Eq. (5)에서 설정한 정상범위 내 최댓값(CCluDes)을 벗어나는 경우가 발생하기 때문이다. 하지만, Average risk와 Resq의 염소 주입 위치에 따른 경향성은 동일 농도인 경우 두 지표간 상관성을 나타내는 Pearson correlation coefficient (PCC) 기준 -0.54~-0.57 사이의 값을 나타내어, 일관적인 경향은 두드러지지 않지만, 두 값이 반대의 경향을 갖는 것으로 보인다.

실제 15번 절점에 1.0 mg/L를 주입할 경우 Resq의 경우 기존 대비 39.06%가량이 감소한다. 이는 해당 재염소 시설 설계 시 바이러스 유입에 대한 대비는 가능하지만, 일반적인 운영에서 설정한 염소 농도 범위를 만족시키기 어려운 경우가 발생하여 또 다른 문제(예: 이취미 민원 등)를 야기할 수 있음을 의미한다.

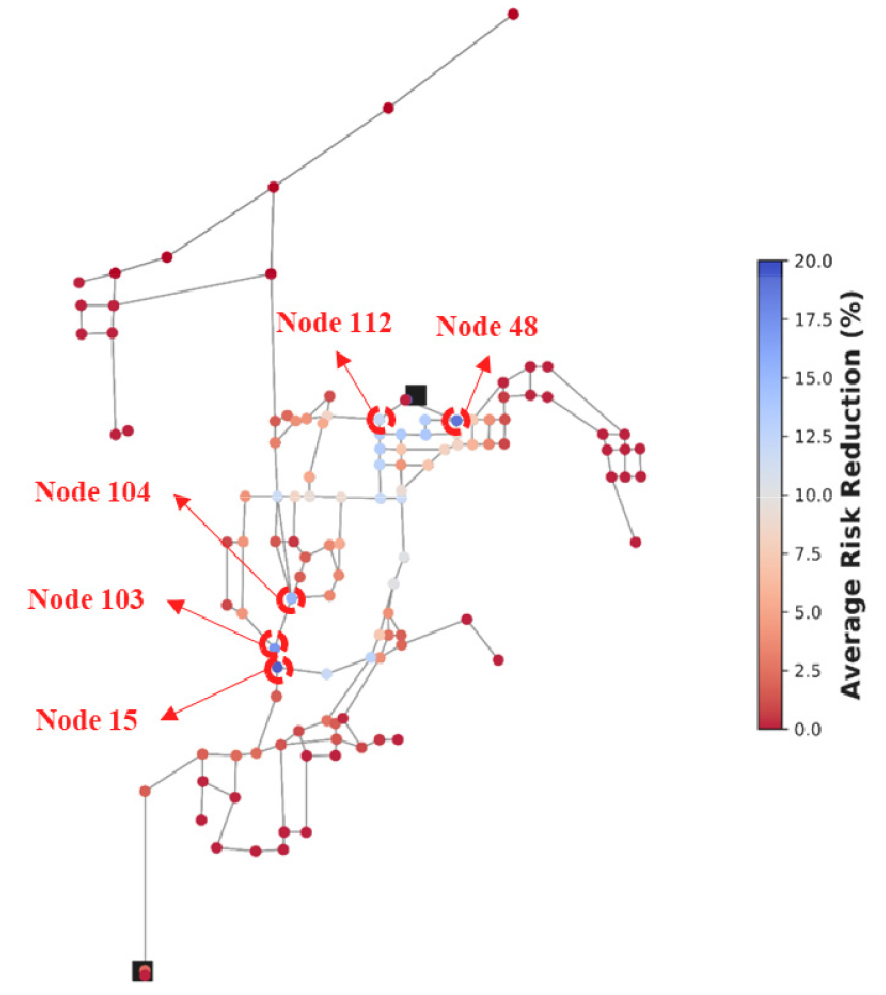
이러한 부분을 종합적으로 고려하였을 때, 112번 절점에 0.5 mg/L를 주입하는 경우가 가장 이상적인 경우로 나타났다. 이 경우 Average risk의 경우 19.06%가량 감소할 수 있으며, Resq의 경우 0.65%가량만 감소하였다. Fig. 10은 112번 노드에 재염소 시설을 설치할 경우 Node risk 저감률에 대한 정보를 표출한다. 해당 그림에서 확인할 수 있듯, 상대적으로 Node risk가 높았던 우상단 탱크 인근 절점에서 20% 이상의 Node risk 저감을 나타내고 있다. 이를 통해 바이러스 유입에 대해 효과적으로 대처할 수 있을 것으로 판단된다.

5. 결 론

본 연구에서는 QMRA를 활용하여 상수도 관망 내 잠재적인 바이러스 유입에 따른 위험도 분석을 수행하고 이를 토대로 재염소 시설을 설계하는 방법론을 제시하였다. 제안한 방법론은 미국의 Bellingham 관망에 적용하였으며, 기존 관망의 위험도 분석과 재염소 시설 설치에 따른 위험도 저감의 총 두 단계로 분석을 수행하였다.

분석결과 재염소 설치 전 Average risk는 0.0154였으며, 위험도의 분포는 탱크의 운영과도 밀접한 연관이 있는 것으로 나타났다. 재염소 시설 설치 후 최대 39.06%의 Average risk를 저감할 수 있는 것을 확인하였다. 다만, 산정한 Average risk와 Resq간의 상관관계 분석결과 두 지표 간 큰 상관성은 확인할 수 없었지만, 대체로 역상관 관계를 나타내어 재염소 시설의 농도가 높은 것이 Resq를 향상 시키지는 않음을 확인하였다. 이를 토대로 최종적으로 112번 절점에 0.5 mg/L의 재염소 시설을 설치하는 것을 권장하였다. 다만, 본 연구에서 는 모든 Node를 재염소 시설의 후보 위치로 모의하였으나, 실제로는 현장의 여건에 따라 재염소 시설 설치가 어려울 수 있다. 따라서 이러한 제한조건 등을 고려하여 보다 현실적인 재염소 시설 설계에 활용할 수 있을 것이다.

또한, 본 연구에서는 가정 사항과 추가 연구가 필요한 부분이 있다. 본 연구는 염소 농도를 특정하여 전수조사를 수행하였지만, 최적화 등의 방법을 토대로 재염소 시설의 시간대별로 염소 농도를 차등 주입하거나 배수지 염소 주입 농도와 재염소 시설 농도를 복합적으로 고려하는 연구로 확장하여 진행할 수 있을 것이다.