1. 서 론
2. 이안류 예측모형
2.1 관측기반 지수산출 알고리즘
2.2 수치모의 시나리오
2.3 수치모의기반 이안류 발생정도
2.4 이안류 위험지수 산출 함수
3. 이안류 지수와 사례 비교분석
3.1 2021년 6월 20일 이안류 지수
3.2 2021년 7월 25일 이안류 지수
3.3 2021년 7월 27일 이안류 지수
3.4 2021년 8월 22일 이안류 지수
4. 요약 및 토의
1. 서 론
여름철 해수욕장에 나타나는 이안류는 해수욕객들에게도 회자될 정도로 심각한 수준의 재난으로 인식되어지고 있다. 특히 해운대에서 매년 관찰되는 이안류는 해수욕장 개장 때 마다 언론에 언급되고 있다. 2007년부터 그 피해가 보도되기 시작하여, 2009년 125명, 2010년 179명, 2012년에 418명, 2013년에 546명, 2014년에 217명의 해수욕객이 해경 및 119 구조대에 의해 구조 및 안전 조치되었다(KHOA, 2018). 그 후 이안류가 재난으로 인식되면서 관측기반 및 기상기반 시스템을 통해 생산된 이안류 발생 예경보를 해양수산부 국립해양조사원에서 제공하고 있으며, 이를 이용하여 해경 및 119구조대는 이안류 사고에 대해 적극적으로 대응하고 있다. 이에 피해 및 구조자의 수가 줄었으나 매년 수명에서 수십 명의 해수욕객이 여전히 이안류로 부터 구조되고 있다(KHOA, 2021).
우리나라에 비해 해수욕객 인구 및 해변의 규모가 큰 미국 및 호주에서는 이안류에 의한 피해가 매우 심각한 수준으로, 이안류 사고로 매년 수십 명의 사망자가 발생하고 있다(Gensini and Ashley, 2010; NOAA, 2022a). 그럼에도 불구하고, 미국 해양기상청 NOAA (National Oceanic and Atmospheric Administration)에서 조차도 완전한 방어 대책을 강구하고 있지 못하는 것으로 보인다(Dalrymple et al., 2011; Castelle et al., 2016). 미국 NOAA에서 제공하는 이안류 예보는 각 지역 해변에 대하여 이안류 발생정도를 3단계로 나누어 작일 오후에 본 예보를 하고 당일 새벽에 수정예보를 제공하는데 그치고 있다. 이러한 예보는 하루 전체에 대해 동일한 예측치로 대응하게 되므로 비효율적일 뿐만 아니라 시시각각 변화할 수 있는 해상상태와 이에 따라 돌발적으로 발생할 수 있는 이안류 대응을 위해서 충분히 정교해 보이지 않는다. 이안류 예측을 위해 기상 및 해상상태와 지형 등을 고려하여 이안류 발생정도를 점수화하는 위험점수 산정법은 많은 연구자들에 의하여 발전되어 왔다(Lushine, 1991; Lascody, 1998; Engle, 2003; Schrader, 2004; Nelko and Dalrymple, 2008). 그러나 해외에서 발생하는 이안류에 의한 피해사례와 현재까지 발표된 이안류 예측 기술수준으로 미루어 해외에서도 아직 이안류를 정확하게 예측하는 방법이 정립되어 있지 않다. 그러나 최근 미해양청에서 일부 지역에 대하여 이안류 예보모형을 운영하기 시작했다는 보도가 있으며(NOAA, 2022b), 이 예보모형은 Moulton et al. (2017)과 Dusek and Seim (2013)을 기초로 하고 있는 것으로 보인다. 이 예보모형은 현장 구조요원들의 설문조사를 통해 구축한 경험함수를 이안류 관측결과와 비교, 분석하여 파고, 파향, 조위에 대한 발생정도 분포를 도출하고, 예보된 파랑자료를 이안류 발생정도 분포에 적용하여 운영한다.
우리나라에서도 매년 이안류에 의한 안전사고가 발생되고 있기 때문에 이안류에 대한 예측체계 구축은 매우 시급한 실정이었고, 이에 국립해양조사원에서는 2011년부터 실시간 관측정보를 바탕으로 이안류의 발생정도를 예측하여 실시간 경보체계를 구축하고, 운영하기 시작하였다. 일반적으로 이안류는 연안 수심지형, 비선형파의 상호작용 및 평균자유수면의 불안정성(instability)등에 기인하여 파랑 에너지가 연안방향으로 강한 비균등성이 형성될 때 발생하는 것으로 이해되고 있다(Dalrymple, 1975, 1978; Tang and Dalrymple, 1989). 최근에는 다양한 원인에 의해 끊어진 파봉선을 갖는 파의 쇄파에 따른 변동이 이안류를 발생시키는 근본적인 메커니즘(Peregrine, 1998; 1999)으로 인식되기 시작했다(Johnson and Pattiaratchi, 2006; Clark et al., 2012; Choi et al., 2015, Choi, 2015; Feddersen, 2014). 따라서 이안류가 예측되기 위해서는 무엇보다도 파랑정보의 정확한 예측이 선행되어야 한다는 것을 의미한다. 이러한 관점에서 상기 경보체계는 예측된 파랑정보가 아닌 실시간으로 관측된 파랑정보를 사용하므로 그 예측 정확도에 장점이 있어, 현장에서 이안류에 의한 입욕통제 판단의 자료로 활용되고 있다.
본 연구에서는 국립해양조사원의 실시간 이안류 경보체계에 장착된 Choi et al. (2013a)와 Choi (2014)를 기반으로 만들어진 이안류 경보지수 함수를 개선하기 위하여, 기존 기법의 각 변수(파고, 주기, 조위, 파향, 주파수 스펙트럼 광협도, 파향 스펙트럼 광협도)에 대한 곡선적합 경험식을 사용하는 대신에, 다변수 함수인 이안류 발생정도를 2차원 분포(예, 파고-주기, 파고-조위, 파고-파향, 파고-주파수 스펙트럼 광협도, 파고-파향 스펙트럼 광협도)로 저장하여 사용하므로 이안류 위험지수 함수를 개선하였다. 2절에서 본 연구에서 사용하는 이안류 예측모형을 기술하고, 3절에 2021년 해운대 파랑 관측자료와 부산조위소의 조위정보를 개선된 방법에 적용, CCTV를 통해 확인된 몇 차례의 이안류 발생사건에 대하여 관측정보 및 적용 결과를 비교하여 제시하였다.
2. 이안류 예측모형
본 절에서는 국립해양조사원에서 운영하고 있는 이안류 경보체계에서 이안류 지수가 산출되는 알고리즘의 구조(2.1절)를 제시하고, 그 알고리즘 안에서 지수를 산출하는 함수를 도출하기 위해 필요한 사전 수치모의의 시나리오(2.2절)와 수치모의 결과인 이안류 발생정도 분포(2.3절)에 대하여 기술하였다. 그리고 기존의 기법과 본 연구에서 사용한 기법을 비교하여 기술하였다(2.4절).
2.1 관측기반 지수산출 알고리즘
국립해양조사원의 이안류 경보체계는 실시간 관측을 입력하므로 이안류 위험지수가 생산되고, 그 정보를 서비스하는 절차를 채택하고 있다. Fig. 1에 이안류 경보체계에서 지수가 산정되는 절차를 간략히 나타낸 흐름도와 그 최종 결과물인 이안류 정보가 웹서비스로 제공되는 화면을 제시하였다. 흐름도에 제시한 것처럼 총 6개의 관측정보(파고, 파주기, 조위, 파향, 주파수 스펙트럼 광협도, 파향 스펙트럼 광협도) (Choi, 2014)를 변수로 하는 근사 함수를 개발하였고, 이를 통해 실시간 관측에 따른 이안류 위험지수가 신속하게 산출되어 그 정보가 서비스되도록 하고 있다. 참고로, 파고와 파주기는 수면변위(2Hz) 5분 시계열을 zero-up-crossing 방법으로 부이 안에서 계산하고, 파향 및 스펙트럼 계수는 자료가 수신된 서버에서 3축 변위(2Hz) 211개의 시계열을 스펙트럼 분석하여 산출한다. 부이에서 상대적으로 짧은 시계열을 사용하는 것은 이안류 예측에 가장 중요한 파고 변화에 신속하게 반응하는 예측결과를 얻기 위함이다. 반면에 파향 및 스펙트럼 특성을 얻기 위한 분석은 상대적으로 긴 시계열을 필요로 하고 부이에서 2개의 독립된 계산을 수행하기에는 전력에 한계가 있어, 3축 변위자료를 수신 받아 계산하고 있다. 조위는 해당 현장에서 가장 가까운 조위관측소의 관측값을 사용한다.
본 연구는 이안류 위험지수가 산출되는 상기 6개 변수에 대한 근사 함수를 새롭게 개선한 것이며, 이 함수에 대해서는 2.3절과 2.4절에 자세히 기술하였다. 상기 6개의 이안류 발생에 영향을 주는 물리량은 관측변수이면서 동시에 수치모의를 위한 입력변수이기 때문에 이 변수들을 이용하여 해상상태 시나리오를 수립하고, Boussinesq 수치모형(FUNWAVE)을 이용한 광범위한 시뮬레이션을 수행하므로 그 결과로부터 이안류 정보를 생산할 수 있다. 이에 관해 다음절에 기술하였다.
2.2 수치모의 시나리오
본 연구의 예측 알고리즘에 따라 관측된 6개의 변수 즉, 파고(H), 파주기(T), 조위(E), 파향(), 주파수 스펙트럼 광협도(F), 파향 스펙트럼 광협도(D)는 이안류 발생에 영향을 주는 물리량으로 관측변수이면서 동시에 수치모의를 위한 입력변수이다. 따라서 이 입력조건들을 이용하여 해상상태 시나리오를 수립하고 그에 따라 수치모의를 수행하였다. Tables 1 and 2에 본 연구에서 해운대 해수욕장의 이안류 발생정도 분포를 도출하기 위해 사용한 해상상태에 대한 시나리오, 즉 수치모의를 위한 조건들을 제시하였다.
너울에 의한 이안류 발생정도를 얻기 위해 규칙파 수치모의를 수행하였고, 풍파에 의한 이안류 발생정도를 얻기 위해 불규칙파 수치모의를 수행하였다. 규칙파 조건에서의 해운대 해수욕장 수치모의를 위해서 너울의 파고는 0.5~1.5 m 범위에서 6개, 파주기는 5~15s 범위에서 6개, 파향은 서~동 범위에서 13개, 조위는 DL기준으로 간조~만조사이에서 7개를 사용하였다. 조위를 반영하기 위해서는 DL 기준으로 구성된 수심격자에 대해 조위를 추가하여 수심정보를 입력하였다. 불규칙파 조건에서의 수치모의를 위해서는 풍파의 파고는 0.7~1.9 m 범위에서 7개, 파주기는 5~15s 범위에서 6개, 주파수 스펙트럼 광협도 조건을 5개, 파향 스펙트럼 광협도 조건을 7개로 사용하였다. 불규칙파 수치모의를 위해 JONSWAP 스펙트럼과 Mitsuyasu et al. (1975)의 방향 분산함수를 사용하였다. 참고로, 모든 조건의 조합을 수치모의하기 위해서는, 예를 들어 6(파고)×6(주기)×11(파향)×7(조위)×13(스펙트럼 광협도와 일방향 및 단주기)개로 실제 모든 경우에 대해 수치모의를 진행하는 것이 어려우므로 파향, 조위, 스펙트럼 광협도를 변화시키며 수치모의를 진행하는 경우에는 11초를 대표주기로 고정하여 시나리오를 구성하였다. 상대적으로 규모가 큰 이안류 발달에 유리하며 그 이상의 긴 주기에서 이안류 발생정도가 크게 증가하지 않은 조건을 채택하였다. 이 부분은 이안류 발생정도 분포를 다루는 다음 절에 그 결과와 함께 다시 언급하였다.
규칙파 1.5 m, 불규칙파 1.9 m 이상의 파고에서는 일반 해수욕객의 입욕이 가능하다고 할 수 없으며, 파주기 15초 이상의 조건에서는 일반적으로 높은 파고를 동반하거나 너울의 범위 이상으로 판단되기 때문에 시나리오에서 제외되는 등 현실적인 조건으로 구성하였다. 참고로, 파고 1.9 m 이상, 파주기 15s 이상의 조건에서는 최대 위험지수가 산정되도록 구성하였다. 위의 시나리오는 해운대 해수욕장을 예로 들어 구성된 결과로, 수치모의의 대상이 되는 해수욕장마다 서로 조금씩 다른 외해 파랑조건을 가지고 있으며, 조위와 파향 조건은 해수욕장 마다 다를 수 있기 때문에 각 지역 특성에 맞도록 이안류 발생이 가능한 범위의 조건으로 시나리오를 구성할 필요가 있다.
본 연구에는 여러 문헌(Yoon et al., 2012; Choi et al., 2012a; Shin et al., 2014; Choi and Roh, 2021)에서 이안류 발달 수치모의를 위해 적용되고 검증된 사례가 있는 수치모형인 FUNWAVE를 사용하였다. 본 연구에서는 다방향 불규칙파에 따른 연안흐름을 연구한 Choi et al. (2015)의 FUNWAVE 버전을 사용하였고, 동일한 경험 파라미터들을 사용하였다. 최근 Choi et al. (2012b, 2013b), Choi (2022)에 해운대 해수욕장 이안류에 대한 수치모의를 자세히 기술하고 있어, 본 논문에서는 수치모의 결과에 대한 제시를 상기 문헌의 내용으로 대체한다.
Table 1.
Scenario of swell and tidal conditions as the input parameters in numerical simulations of regular wave-induced rip currents (The elevation is on the datum level, the angle 0° indicates the wave direction of perpendicular to the shoreline, and the bracket indicates the number of cases varied with each parameter.)
Table 2.
Scenario of wind wave and tidal conditions as the input parameters for numerical simulations of random wave-induced rip currents (The elevation is on datum level, the angle 0° indicates the wave direction of perpendicular to the shoreline, and the bracket indicates the number of cases varied with each parameter.)
2.3 수치모의기반 이안류 발생정도
각 시나리오 조건에 대한 수치모의 결과인 유속분포로 부터 이안류 발생에 대한 대표값을 정량화할 필요가 있기 때문에 다음과 같은 방법으로 이안류 발생정도를 도출하였다. 먼저 수치모의의 계산영역 최대 이안류 유속(해안선의 직각방향 유속)을 시계열로 나타내었다. 4개 조건의 수치모의 결과로부터 계산된 시계열이 Fig. 2에 제시되었다. 각각 이안류 수치모의 시간을 분모로 하고 임의의 위험 유속을 초과한 최대 이안류 유속이 지속되는 시간을 분자로 하는 비율, 즉 이안류 발생정도를 계산하여(Choi, 2014) 정량화하였다. 여기서, 위험 유속은 해수욕객이 이안류에 의해 외해로 끌려 나갈 수 있는 유속을 상정한 것으로 0.6, 0.9, 1.2, 1.5, 1.8 m/s로 가정하여 각각의 이안류 발생정도 평균을 계산하였고, 그 결과를 Table 3에 제시하였다. 다양한 위험유속을 사용한 것은 해수욕객의 상황(신체조건, 연령, 성별 및 튜브 착용 유무 등)에 따라 그 위험 유속을 특정하기 힘들기 때문임을 밝힌다.
Fig. 3에 상기 기술한 절차로 도출된 해운대 해수욕장 이안류 수치모의 기반의 이안류 발생정도를 파고와 각 변수들에 따른 2차원 분포로 도시하였다. 패널(a)는 규칙파 수치모의를 통한 너울의 파고-파주기 분포(fSHT), 패널(b)는 불규칙파 수치모의를 통한 풍파의 파고-파주기 분포(fWHT), 패널(c)는 규칙파 수치모의를 통한 파고-조위 분포(fHE), 패널(d)는 규칙파 수치모의를 통한 파고-파향 분포(), 패널(e)는 불규칙파 수치모의를 통한 파고-주파수 스펙트럼 광협도 분포(fHF), 패널(f)는 불규칙파 수치모의를 통한 파고-방향 스펙트럼 광협도 분포(fHD)를 나타낸다. 제시된 파고 및 파주기에 따른 이안류 발생정도 분포를 살펴보면 입사파의 파고가 높고 주기가 길수록 이안류 발생정도가 상승됨을 알 수 있다. 이것은 쇄파에 의해 파랑유도 잉여운동량 플럭스(wave-induced excess momentum flux)의 기울기가 커지면 이안류의 규모가 커지기 때문이다. 그리고 풍파를 상정한 불규칙파 조건의 경우에 비해 너울을 상정한 규칙파 조건의 경우가 상대적으로 이안류 발생정도가 높음을 알 수 있다. 이것은 불규칙파의 쇄파가 규칙파의 쇄파보다 완만한 분포를 가지고 있어 상대적으로 약한 이안류를 생성시키기 때문이다. 참고로 약 11초 보다 높은 주기에서 나타나는 주기 상승에 따른 이안류 발생정도 상승이 크지 않기 때문에 앞서 언급한 11초를 대표주기로 상정하여 시나리오를 구성하였음을 밝힌다. 조위에 따른 이안류 발생정도 분포를 살펴보면, 간조 시의 이안류 발생정도가 만조 시의 이안류 발생정도에 비해 상대적으로 크게 나타난다. 이것은 일반적으로 간조시의 해안선 단면경사가 완만해 지기 때문이다. 파향에 따른 이안류 발생정도 분포를 살펴보면, 파가 대체로 해안선에 직각으로 입사할 때 이안류가 잘 발생하며 파향에 따라 차이가 발생하는 것으로 나타난다. 이것은 경사 입사하는 경우에는 일반적으로 해안선을 따라 한쪽 방향으로 흐르는 연안류가 지배적으로 나타나기 때문이다. 참고로 조위와 파향에 따른 결과는 상대적으로 발생정도가 높게 나오는 규칙파 모의를 통해서 도출하였다. 이러한 이안류 발생정도의 경향은 Dusek and Seim (2013)의 그것과 동일하다. 상기 참고문헌에는 고려하지 않고 있는 스펙트럼에 따른 이안류 발생정도의 특성은 다음과 같다. 주파수 및 파향 스펙트럼이 협대역일수록 즉, 너울에 가까울수록 이안류 발생정도가 높으며, 그 변동은 다른 변수에 의한 분포보다 상대적으로 급하지 않은 기울기를 보인다. 제시된 분포로부터 이안류 발생정도의 특성을 알 수 있으며, 이러한 분포를 데이터베이스 함수화하면 해상조건 시나리오에 대한 이안류 발생정도를 산출할 수 있게 된다. 본 연구에서는 실제 관측자료들을 활용하여 해당 데이터베이스 함수를 지수화하였고 이를 통해 데이터베이스 함수를 실제 이안류 발생에 대한 예경보에 활용할 수 있게 하였다. 다음 절에 기존 이안류 지수함수와 이 새롭게 고안된 데이터베이스 함수에 대하여 비교하여 기술한다.
Table 3.
The rip current likelihoods according to the input parameters for the FUNWAVE simulation results shown in Fig. 2
| No | Regular waves | ||||
| Height (m) | Period (s) | Direction | Tide (m) | Likelihood (%) | |
| 1 | 0.5 | 5 | S | 0 (DL) | 3 |
| 2 | 0.5 | 7 | S | 0 (DL) | 38 |
| 3 | 0.6 | 9 | S | 0 (DL) | 58 |
| 4 | 0.7 | 11 | S | 0 (DL) | 85 |
2.4 이안류 위험지수 산출 함수
2.4.1 기존 이안류 위험지수 함수
Choi et al. (2013a)은 2.3절에 기술된 이안류 발생정도 분포를 이용하여 파고, 주기, 조위를 변수로 하는 이안류 발생정도 경험함수를 곡선적합법(curve fitting method)을 이용하여 도출하였다. 그리고 이 경험함수들을 조합하는 지수함수를 제안하여 이안류 위험지수를 생산하였다. Choi (2014)에서는 파향, 주파수 및 파향 스펙트럼 광협도를 변수로 하는 경험함수를 곡선적합법으로 도출하여, 지수함수에 추가하여 개선하였다. 상기 문헌에서 Eq. (1)을 각 변수에 따른 이안류 발생정도 경험함수로 선택하고, 각 계수들을 앞 절에서 기술한 수치모의 결과인 이안류 발생정도 분포를 이용하여 곡선적합법으로 결정하였다.
여기서 X는 상기 언급한 관측변수인 파고 H, 주기 T, 조위 E, 파향 , 주파수 광협도 F, 파향 광협도 D가 적용될 수 있으며, 는 곡선적합법으로 결정되는 계수이다. 앞서 기술한 바와 같이 파고에 대한 이안류 발생정도 경험식 , 주기에 대한 이안류 발생정도 경험식 , 조위에 대한 이안류 발생정도 경험식 , 파향에 대한 이안류 발생정도 경험식 , 주파수 광협도에 대한 이안류 발생정도 경험식 , 파향 광협도에 대한 이안류 발생정도 경험식 이 도출되었다. 참고로, Eq. (1)은 최소값 0으로 부터 최대값 1로 서서히 변화는 함수로 각 변수에 대하여 이안류 발생정도를 백분율로 나타내기 적합하여 선택되었다(Choi et al., 2012a). 이렇게 도출된 이안류 발생정도 경험함수들은 다음의 지수함수 Eq. (2)를 통해 조합되어 최종 이안류 위험지수가 산출된다(Choi et al., 2013a).
여기서 R은 이안류 지수이며, 는 지수의 현실화를 위한 경험상수로 이안류 발생시점의 영상 자료들을 이용하여 경험적으로 결정하였다. 관측치의 부분 누락 등의 문제를 저감하기 위해 파고와 주기에 대하여 서로 독립인 CT와 CH 항을 추가하였다. 또한 이 위험지수는 이안류의 발생정도를 나타내는 지수이면서 동시에 해수욕 활동의 안전지수 역할을 할 수 있어야 하므로 백분율로 구성된 각각의 이안류 발생정도 함수들과 다르게 백분율로 나타내지 않았다. 즉, R이 이안류 발생정도 백분율의 추정함수이기는 하지만 위험을 나타내는 지수로 규정하고 최대값을 100이 아닌 120으로 고정하여 적용하였다.
2.4.2 개선된 이안류 위험지수 함수
기존에 채택하여 사용하고 있는 곡선적합법을 이용한 이안류 발생정도 경험식은 실제 6개의 관측변수에 따른 6차원 함수를 대체하기 위한 1차원 함수들의 조합이라는 한계와 경험계수가 많다는 문제점이 있다. 즉 6개의 경험식에 각각 4개의 곡선적합 계수가 있어 총 24개의 경험계수가 필요하다. 따라서 이러한 경험계수를 사용하는 대신에, 본 연구에서는 더 많은 조건에 대해 수치모의를 수행하여 2차원 함수 즉, 2.3절에 제시한 것과 같은 이안류 발생정도 분포를 도출하여 이를 저장하고, 그 결과를 추출하여 조합하는 데이터베이스 함수기법을 제안하고 사용하였다. 이안류 발생정도를 나타내는데 가장 중요한 변수인 입사파 파고를 주 변수로 하여 각각의 다른 변수에 대해 2차원 이안류 발생정도 분포, 즉 Fig. 2와 같은 분포를 수치모의 결과로 도출하여 저장하여 사용하였다. 시나리오에 따른 수치모의 결과로부터 얻어진 이안류 발생정도를 파고-파주기(fSHT 또는 fWHT), 파고-조위(fHE), 파고-파향(), 파고-주파수 스펙트럼 광협도(fHF), 파고-방향 스펙트럼 광협도(fHD)의 2차원 분포로 구성하고 이를 데이터베이스화하여 사용하면, 1차원 경험함수를 사용하는 한계를 극복하고 이론적으로 6차원 이안류 발생정도 함수에 상대적으로 가까운 정도 높은 지수를 생산할 것으로 판단하였다. 또한, 파고-파주기의 이안류 발생정도 분포는 너울을 상정한 일방향 규칙파 조건에서의 분포(fSHT)와 풍파를 상정한 다방향 불규칙파 조건에서의 분포(fWHT)를 나누어 도출하였다. 6개의 2차원 이안류 발생정도 분포 fSHT (H,T), fWHT (H,T), fHE(H,E), (H,), fHF (H,F), fHD (H,D)를 조합하여, 6차원 이안류 발생정도 함수의 근사를 위해 다음과 같은 지수 함수를 채택하였다.
여기서 S는 이안류 발생지수, 이안류 발생정도 2차원 분포를 조합하기 위해 사용하는 는 경험상수로 현장 이안류 발생 영상자료들로부터 각 분포의 가중치를 평가하여 경험적으로 결정하였다. 는 고려하는 입사파가 너울인지 풍파인지 구별하기 위해 주파수 스펙트럼 광협도와 파향 스펙트럼 광협도의 함수가 되는 것이 이론적으로 적합하다. 다시 말해, 스펙트럼 광협도 분석을 통해 너울 또는 풍파의 입사를 판정하여 적용하는 것이 이론적으로는 적합하다. 그러나 실제 너울과 풍파가 혼합되어 입사하는 경우도 흔하게 관찰되며, 부이관측 및 스펙트럼 분석기법 등의 한계로 너울과 풍파를 정확하게 구별하는 것도 쉽지 않기 때문에 너울 분포와 풍파 분포를 동시에 고려하는 것이 안전을 목적으로 하는 예경보 체계에서는 합리적일 수 있다고 판단하였다. 부연하자면, 일반적인 파랑부이는 한 위치에서 3개의 변위를 계측하여 분석하는 체계를 가지고 있고 따라서 Yoon et al. (2012)에서 밝힌 바와 같이 파향 스펙트럼 분석기법으로 Longuet-Higgins et al. (1963)를 채용하게 되며, 이 기법을 통해 산정된 파향 스펙트럼의 분포형상은 신뢰도가 높지 않다고 알려져 있다. 물론 첨두파향에 대해서는 일반적으로 그 값이 유의미하며 타당하다고 알려져 있다. 참고로 이안류 경보체계에서는 Longuet-Higgins et al. (1963)에 따라 스펙트럼을 추정하고 외해로 향하는 파랑의 에너지밀도를 제거하여 해안으로 들어오는 180도의 파향 스펙트럼만을 이용하여 첨두파향을 산정하여 사용하였다. 본 논문에서 제시하는 해운대 해수욕장의 지수함수에서는 를 사용하고, =1.2의 보수적 안전계수를 추가하여 사용하였다.
참고로, 지수에 따른 경보단계를 이 지수 값들을 기준으로 관심(S < 30), 주의(30≤S < 55), 경계(55≤S < 80), 위험(80≤S < 120)으로 나누어 경보 서비스를 실시하고 있다. 지수의 단계 구분은 유관기관의 통제 등 판단의 기준이 되는 정보를 위해서 그리고 대국민 서비스의 위험에 대한 가독성을 높이기 위해 경험적으로 설정되었음을 밝힌다.
3. 이안류 지수와 사례 비교분석
국립해양조사원의 2021년 이안류 감시체계로부터 확보된 CCTV 영상을 이용하여 대표적으로 이안류가 발생한 6월 20일, 7월 25일, 27일, 8월 22일의 이안류 발생영상, 관측자료 그리고 본 연구에서 고안한 기법을 적용한 이안류 지수를 제시하고 분석하였다.
3.1 2021년 6월 20일 이안류 지수
2021년 6월 19일에는 약한 이안류가 여러 차례 발생했던 것으로 확인되며, Fig. 4에 당시 10시 40분과 11시 50분경에 발생한 이안류가 촬영된 영상자료를 제시하였다. Fig. 5에는 6월 17일의 이안류 경보지수를 비롯하여 관측된 파고, 주기, 조위, 파향과 주파수 및 파향 스펙트럼 광협도가 도시되어 있다. Fig. 5의 첫 번째 패널에 기존의 경험함수 기반 지수와 DB함수 기반 이안류 지수를 비교하였다. 이안류가 발생하는 것으로 판단되는 시간에 지수의 상승을 확인할 수 있으며, 30이상(“주의”단계)을 나타내고 있으므로 적절한 경보역할을 하였다고 판단된다. 또한, 이안류 지수를 살펴보면, 본 연구의 DB함수 기반 이안류 지수가 전체적으로 높아 본 연구의 이안류 지수를 적용할 경우에 조금 더 안전한 경보를 내릴 수 있다고 판단된다.
관측 시계열과 함께 지수의 변화를 살펴보면, 상대적으로 주기와 파고 값은 클 때, 조위는 저조위일 때 이안류 지수가 상승하며, 이것은 앞서 설명한 것처럼 주기와 파고 값이 클수록, 조위는 낮을수록 이안류의 발생가능성이 커지기 때문이다. 파향 0도는 남쪽으로부터 들어오는 S파향을 의미하고 +90도는 E파향을 그리고 -90도는 W파향을 의미한다. 주파수 스펙트럼 광협도 계수는 그 값이 클수록, 파향 스펙트럼 광협도 계수는 그 값이 작을수록 협대역 스펙트럼을 의미한다. 이안류가 발생했을 때의 파향과 스펙트럼 광협도를 보면, 파향은 해안선에 직각방향인 S파향에 가깝고, 주파수 스펙트럼 광협도는 급하게 상승하는 부분들이 관찰되며, 파향 스펙트럼 광협도는 큰 변화가 없는 것으로 보인다. S파향의 협대역 스펙트럼이 나타날 때, 즉 남쪽에서 너울이 입사할 때 이안류가 잘 발생하는 것으로 알려져 있다. 참고로, Goda (2010)는 첨두증폭계수 가 3.0이상인 스펙트럼을 너울성 스펙트럼(swell spectrum)으로 분류하고 있으므로, 상기 이안류 발생시 주파수 스펙트럼은 협대역이라고 볼 수 있다.

Fig. 5.
Time series of rip-current likelihood index (first panel) and observations (significant wave period (second panel); significant wave height (third panel); tidal elevation (black line) and wave direction (red line) (fourth panel); spreading of frequency spectrum (blue line) and spreading of directional spectrum (red line) (fifth panel)) of the 20th of June, 2021. In the first panel, the gray line indicates the previous index and the black line indicates the present index. The gray broken lines of 30, 55 and 80 emphasize rip current warning levels. The wide green bands indicate the rip current events in Fig. 4
3.2 2021년 7월 25일 이안류 지수
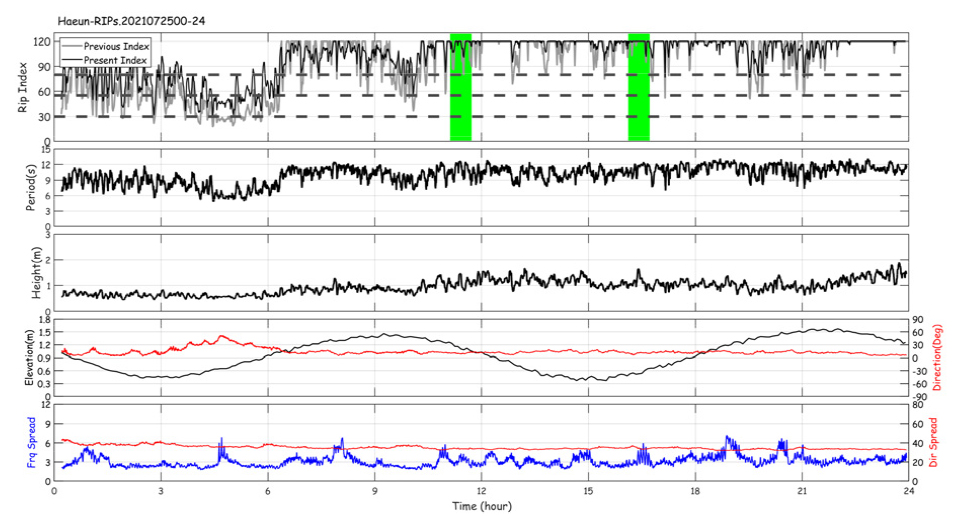
2021년 7월 25일에 강한 이안류가 수차례 발생했던 것으로 확인되며, Fig. 6에 당시 11시 25분과 16시 25분경에 발생한 이안류가 촬영된 영상자료를 제시하였다. Fig. 7에는 7월 25일의 이안류 경보지수를 비롯하여 관측된 파고, 주기, 조위, 파향과 주파수 및 파향 스펙트럼 광협도가 도시되어 있다. Fig. 7의 첫 번째 패널에 기존의 경험함수 기반 지수와 DB함수 기반 이안류 지수를 비교하였다. 이안류가 발생하는 것으로 판단되는 시간에 지수의 상승을 확인할 수 있으며, 80이상(“위험”단계)을 나타내고 있으므로 적절한 경보역할을 하였다고 판단된다. 제시된 것과 같이 지수가 높은 경우에는 두 기법의 지수에 큰 차이가 없어 보인다.
이안류의 발달이 확인되는 환경에서 관측과 지수의 변화를 살펴보면, 파고가 높고 주기가 긴 파가 입사하는 것을 알 수 있다. 또한 S파향 즉, 해변에 직각에 가깝게 입사하는 환경을 보여 준다. 파고가 크고 주기가 긴 경우에는 조위에 따른 수심이 큰 영향을 주는 것으로 보이지 않는다. 주파수 스펙트럼의 변화가 상대적으로 크고 폭이 좁은 협대역일 때 이안류의 발생이 잘 관찰된다. 다만, 앞서 언급한 것과 같이 부이관측의 한계로 분석된 스펙트럼 광협도의 변동이 크지 않아 파향 스펙트럼의 변화 특성은 찾기 어려워 보인다.
3.3 2021년 7월 27일 이안류 지수
2021년 7월 27일에도 이안류가 수차례 발생했던 것으로 확인되며, Fig. 8에 당시 13시 27분과 16시 46분경에 발생한 이안류가 촬영된 영상자료를 제시하였다. Fig. 9에는 7월 27일의 이안류 경보지수를 비롯하여 관측된 파고, 주기, 조위, 파향과 주파수 및 파향 스펙트럼 광협도가 도시되어 있다. Fig. 9의 첫 번째 패널에 기존의 경험함수 기반 지수와 DB함수 기반 이안류 지수를 비교하였다. 이안류가 발생하는 것으로 판단되는 시간에 지수의 상승을 확인할 수 있으며, 55이상(“경계”단계)을 나타내고 있으므로 적절한 경보역할을 하였다고 판단된다. 이 범위에서 두 기법의 지수는 차이를 보이며, 새로 고안된 기법의 지수가 높아 보수적으로 안전한 경보를 내릴 수 있다고 판단된다.
이안류의 발달이 확인되는 환경에서 관측 시계열과 지수의 변화를 살펴보면, 파고는 상대적으로 높지 않지만 긴 주기의 파랑이 입사하여 이안류가 발생했다. 또한 S파향 즉, 해변에 직각에 가깝게 입사할 때 그리고 조위가 상대적으로 낮은 경우에 이안류가 잘 관찰된다. 제시된 시간의 이안류 발생시점에서는 주파수 스펙트럼 및 파향 스펙트럼 광협도에는 큰 변화가 발견되지 않았다. 참고로, 이러한 경우가 관찰되기도 하기 때문에 Eq. (3)에 채택한 주파수 및 파향 스펙트럼의 가중치 계수가 상대적으로 낮게 설정되었다.
3.4 2021년 8월 22일 이안류 지수
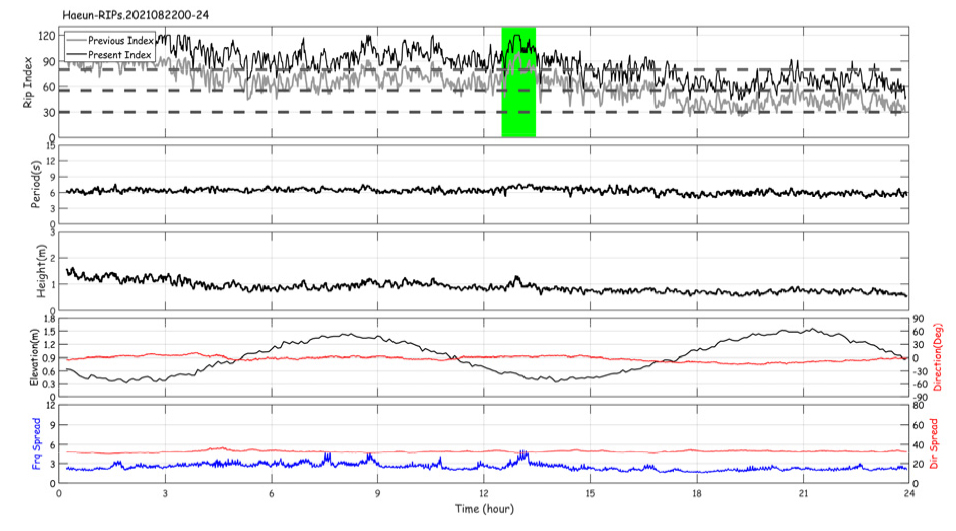
2021년 8월 22일에도 이안류가 수차례 발생했던 것으로 확인되며, Fig. 10에 당시 12시 48분과 13시 9분경에 발생한 이안류가 촬영된 영상자료를 제시하였다. Fig. 11에는 8월 22일의 이안류 경보지수를 비롯하여 관측된 파고, 주기, 조위, 파향과 주파수 및 파향 스펙트럼 광협도가 도시되어 있다. Fig. 11의 첫 번째 패널에 기존의 경험함수 기반 지수와 DB함수 기반 이안류 지수를 비교하였다. 이안류가 발생하는 것으로 판단되는 시간에 지수의 상승을 확인할 수 있으며, 80이상(“위험”단계)을 나타내고 있으므로 적절한 경보역할을 하였다고 판단된다. 이 이안류 발생환경에서도 새로 고안된 기법의 지수가 높으며 보수적으로 안전한 경보를 내릴 수 있다고 판단된다.
이안류의 발달이 확인되는 환경에서 관측 시계열과 지수의 변화를 살펴보면, 시나리오에서 상정한 입사파 조건과 비교하여 중간 정도의 규모인 1 m 파고 7s 주기 정도의 파랑이 입사하여 이안류가 생성되었고 상대적으로 해변에 직각에 가깝게 입사하고 조위가 상대적으로 낮은 경우에 이안류가 관찰되었다. 또한 주파수 스펙트럼의 변화가 상대적으로 크고 폭이 좁은 협대역일 때 이안류의 발생이 관찰되었다.
4. 요약 및 토의
본 논문에서는 이안류 안전사고 저감을 위해 운영되는 실시간 이안류 경보체계를 소개하고, 경보체계의 이안류 위험지수를 생산하는 방법을 개선하였고, 그 결과를 제시하였다. 상기 체계는 실시간 관측정보를 사용하므로 신속한 이안류 위험지수를 생산하기 위해 사전에 수행된 수치모의 결과 즉, 해상 시나리오에 따른 이안류 발생정도를 이용한다. 다변수 함수인 이안류 발생정도를 2차원 분포(파고-주기, 파고-조위, 파고-파향, 파고-주파수 스펙트럼 광협도, 파고-파향 스펙트럼 광협도)로 저장하여 DB함수로 사용하였다. 2021년의 해운대 파랑관측 자료와 부산조위소의 조위정보를 적용하였고, CCTV를 통해 확인된 몇 차례의 이안류 발생사건에 대하여 영상자료와 위험 지수를 제시하였다. 그 결과, 이안류가 발생하는 것으로 판단되는 시점에서의 지수는 적절한 경보역할을 할 수 있는 정도로 상승함을 알 수 있었다. 기존의 기법의 결과와 비교할 때, 그 경향성에 있어서 큰 차이를 보이지는 않았다. 그러나 기존의 기법에 비하여 경험계수를 크게 줄이므로 알고리즘 도출과정의 비합리성을 감소시킬 수 있다고 판단되었다. 서론에서 밝힌 바와 같이 여러 문헌에서 FUNWAVE를 이용한 이안류 수치모의 결과가 관측 결과에 대해 충분히 정확하다는 검증이 이루어졌기 때문에, 검증된 수치모의 결과를 가능한 더 활용하여 경험계수를 줄여 이안류 지수를 도출하는 것이 합리적이라고 판단하였다.
앞서 언급한 것처럼 현재 이안류 감시체계를 구동하기 위해 운영 중인 파랑부이는 한 위치에서 3개의 변위를 계측하여 분석하는 알고리즘을 가지고 있다. 따라서 일반적으로 파향에 대해서는 타당하다고 알려져 있지만, 산정된 파향 스펙트럼의 분포형상은 신뢰도가 높지 않다. 또한, 실시간 관측에 의존하므로 정확도에 장점이 있지만 이안류 사건에 대해 미리 대비할 수 있는 시간에 여유가 없는 단점도 있다. 그리고 실시간 통신의 특성상 자료의 지체 및 누락의 가능성도 문제가 될 수 있다. 실시간 이안류 경보와 더불어 대응시간의 여유를 위해 파랑예보를 사용하여 사전예측 시간이 확대될 필요가 있다.
해변에서 발생하는 모든 이안류의 발생 시점과 위치를 예측하는 것이 불가능하기 때문에, 발생할 이안류를 시간에 따라 선택적으로 이동하여 관측하는 것도 불가능하다. 더욱이 해변전체에 대해 실시간으로 이안류의 공간적 분포를 관측하는 것도 불가능하기 때문에, 이안류의 발생위험에 대응하기 위한 수단으로 본 논문에서 다루는 파랑정보를 이용한 이안류 예측이 필요하다. 이러한 관점에서, 이안류 예측의 검증을 위한 이안류 강도 및 발생여부에 대한 관측 정보를 얻는 것도 한계가 있음을 밝힌다. 현재 이안류 발생여부를 판단하기 위해 촬영된 영상정보를 사용하고 있으나, 영상자료의 촬영 위치에 따라 정상보정 등의 한계(촬영경사, 파랑 및 조위에 따른 해수면의 변동 등)가 있을 뿐만 아니라 시각적으로 확인되는 이안류보다는 시각적으로 확인되기 힘든 이안류가 많다. 즉, 파랑 거품의 이동이나 분포특성만으로 모든 이안류의 발생여부를 판단하는 것은 가능하지 않다. 다시 말해, 검증을 위한 이안류 발생의 참값을 생산할 수 있는 방법에 한계가 있다. 다만, 영상자료 인공지능 분석을 통해 시각적으로 확인되는 두드러진 이안류 사건에 대한 포착이 가능한 것으로 보이며 이 기술을 이용한 개선점이 있을 수 있다고 판단된다. 나아가, 가까운 미래에 기후변화 때문에 우리나라도 아열대로 변화할 것이고, 삶의 질적 향상으로 레저를 즐기는 해수욕객 수가 계속 증가할 것이므로 이러한 이안류 예측체계를 지속적으로 개선해 나가야 할 필요가 있다.